3.3 波的干涉和衍射 课件 高中物理鲁科版(2019)选择性必修一(共28张PPT)
文档属性
| 名称 | 3.3 波的干涉和衍射 课件 高中物理鲁科版(2019)选择性必修一(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 27.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
第3章 机械波
3.3 波的干涉和衍射
时常会看到这样的现象:
几列水波相遇时,波形会发生变化,
水波脱离接触,又会恢复原来的形态。
为什么产生这样的现象呢?
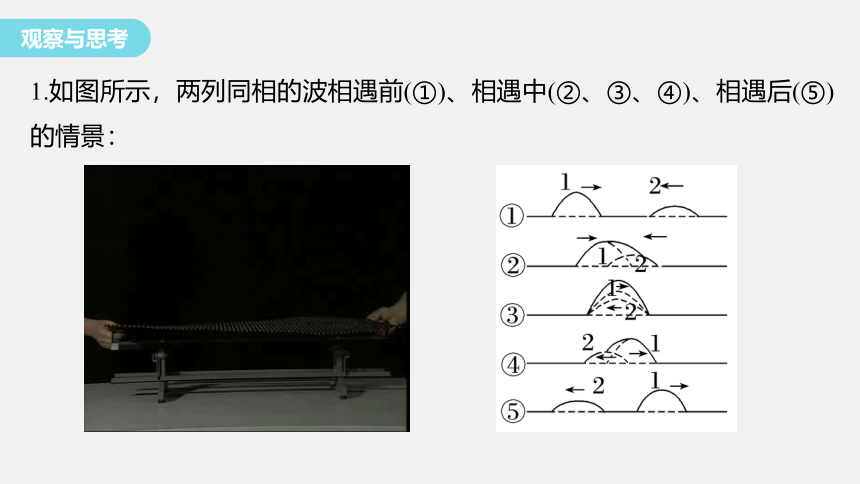
1.如图所示,两列同相的波相遇前(①)、相遇中(②、③、④)、相遇后(⑤)的情景:
(1)比较两列波相遇前(①)与相遇后(⑤)的波形有什么关系?
两列波相遇前、相遇后的波形各自相同。
两列同相波叠加,振动加强、振幅增大。
(2)观察两列同相波的相遇中(②、③、④),振动是加强还是减弱的?振幅是增大还是减小的?
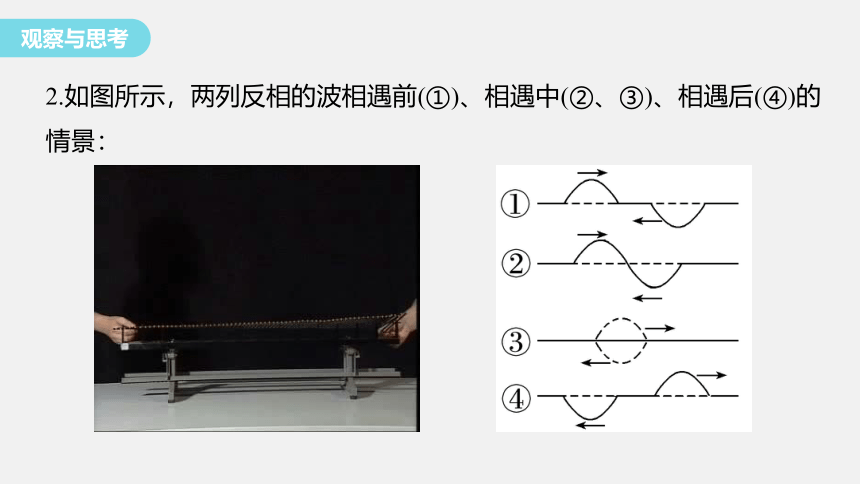
2.如图所示,两列反相的波相遇前(①)、相遇中(②、③)、相遇后(④)的情景:
(1)比较两列波相遇前(①)与相遇后(④)的波形有什么关系?
两列波相遇前、相遇后的波形各自相同。
(2)观察两列反相波的相遇中(②、③),振动是加强还是减弱的?振幅是增大还是减小的?
两列反相波的叠加,振动减弱,振幅减小。
[梳理与总结]
1.波的独立传播性
几列波在介质中传播,相遇后
。
仍能保持各自原有的运动特征(波长、频率、振幅等)不变并继续传播
2.波的叠加原理
在几列波相遇的区域里,介质中的质点同时参加相遇的波列的振动,质点的位移等于 。
相遇波列单独存在时在该处引起的位移的矢量和
声波在相互交错、叠加后互不影响,仍保持原来的性质向前传播。这种现象体现了波传播时具有独立性。
“风声、雨声、读书声,声声入耳”体现了波的什么性质?
(1)在两列波重叠的区域里,任何一个质点的位移都等于原来位移的2倍。( )
(2)两列波叠加时,质点的位移一定增大。( )
(3)只有频率相同的两列波才可以叠加。( )
(4)两列波相遇后各自的传播特点不会受到影响。( )
×
√
×
×
1.(多选)如图所示为两列相向传播且振幅、波长都相同的横波,它们相遇后,下列图像可能存在的是
√
√
波的叠加原理是波具有独立传播性的必然结果,由于总位移是各个位移的矢量和,所以叠加区域的质点的振幅可能增大,也可能减小。
(1)两列同相波叠加,振动加强,振幅增大。
(2)两列反相波叠加,振动减弱,振幅减小。
视频中手带动两个小球振动时,会产生振动方向、振动频率都相同的两列水波。观察这两列波叠加时的现象。
在振动的水面上,出现了一条条从两个波源中间扩散开的相对平静的区域和剧烈振动的区域,这两种区域相互间隔,并且出现的位置是固定的。
1.波的干涉的定义:振动频率和振动方向相同的两列波叠加后,振动加强和振动减弱的区域互相 、稳定分布的现象,称为波的干涉,形成的图样称为干涉图样。
2.产生干涉的条件: 和 相同的波。
间隔
频率
振动方向
3.干涉图样(如图)的特征
(1)加强区和减弱区的位置固定不变。
(2)加强区始终 ,减弱区始终 (加强区与减弱区不随时间变化)。
(3)加强区与减弱区互相 。
4.干涉现象是波的重要特征之一。
加强
减弱
间隔
1.振动加强点和振动减弱点的振幅有什么特点?能不能认为振动加强点的位移始终最大,振动减弱点的位移始终最小?为什么?
振动加强点:振动的振幅等于两列波振幅之和,A=A1+A2。振动减弱点:振动的振幅等于两列波振幅之差的绝对值,A=|A1-A2|。
不能,振动加强(减弱)点是指质点的振幅最大(小),而不是指振动的位移最大(小),因为位移是在时刻变化的,加强点和减弱点的位移均可以为零,只有发生干涉的两列波振幅大小相等,减弱点位移才始终为零。
2.如果两个波源频率不同,会不会出现振动总是加强与总是减弱的区域?为什么?
不会。如果两列波频率不同,在相遇点两列波的相位差会发生变化,不存在波峰总是与波峰相遇或波峰总是与波谷相遇的情况。
3.图中表示两列频率相同的横波相遇时某一时刻的情况,实线表示波峰,虚线表示波谷,此时M点是波峰与波峰相遇的点,是凸起最高的位置之一。
(1)半个周期后,图中六个点中,哪些点具有最大正向位移?哪些点具有负向最大位移?哪些点比较“平静”?
半个周期后,K、P点具有正向最大位移,M、Q具有负向最大位移,H、N点比较“平静”。
(2)随着时间的推移,原来M点这个凸起最高的位置在向哪个方向移动?是不是M质点在向那个方向迁移?M质点在哪个方向上运动?
凸起的最高点由M向P移动,M点并不随波迁移,而只在垂直于纸面的方向上运动。
(3)由图中时刻经过 时,M质点的位移有什么特点?
位移为0
2.(2023·福建漳州市高二月考)如图为振幅、频率相同的两列横波在t=0时刻相遇时形成的干涉图样,实线与虚线分别表示波峰和波谷,已知两列波的振幅均为5 cm,波速和波长均为1 m/s和0.4 m。下列说法正确的是
A.P点始终处于波谷
B.R、S两位置可以处于波谷状态
C.Q点在t=0.2 s时刻将处于波谷位置
D.从t=0到t=0.2 s的时间内,Q点通过的路程为10 cm
√
3.(2022·河北遵化第一中学高二月考)如图所示,S1、S2为两个振动情况完全相同的波源,两列波的波长都为λ,它们在均匀介质中产生干涉现象,S1、S2在空间中共形成了5个振动加强的区域,如图中实线所示。P是振动加强区域中的一点,由图可知
A.P点到两波源的距离差等于1.5λ
B.S1发出的波的传播速度大于S2发出的波的传播速度
C.P点此时刻振动最强,经过半个周期后,P点振动变为最弱
D.当一列波的波峰传到P点时,另一列波的波峰也一定传到P点
√
r1
r2
P
S1
S2
振动加强点和振动减弱点的判断
(1)条件判断法:振动频率相同、振动情况完全相同的两波叠加时,设点到两列波源的路程差为Δr,当Δr=|r2-r1|=kλ(k=0,1,2,…)
时为振动加强点;当Δr=|r2-r1|=(2k+1) (k=0,1,2,…)时为振动
减弱点。若两波源振动步调相反,则上述结论相反。
(2)现象判断法:若某点总是波峰与波峰或波谷与波谷相遇,该点为振动加强点,若总是波峰与波谷相遇,则为振动减弱点。
绕过障碍物传播
通过孔隙,传播范围变宽
波在传播过程中遇到障碍物时波的行为会发生什么变化?
1.定义
波绕过 或通过 继续传播的现象,称为波的衍射。
2.发生明显衍射现象的条件
障碍物或狭缝的尺寸跟 相差不大,或者比波长 。
3.一切波都能发生衍射,衍射是波 的现象。衍射现象只有“明显”与“不明显”之分。
障碍物
孔隙
波长
更小
特有
1.如果孔比波长大很多,波就不会发生衍射现象,这种说法对吗?
不对,一切波都能发生衍射,衍射是波特有的现象。孔比波长大很多时,衍射现象依然存在,只是无法观察到明显的衍射现象。
2.如果孔比波长小很多,一定能观察到明显的衍射现象吗?
不一定,如果孔比波长小的太多,绕过障碍物的波的能量较弱,也不易观察到明显的衍射现象。
3.为什么声波容易发生明显衍射现象?
声波的波长为1.7 cm~17 m,与一般障碍物的尺寸相比差不多,或比其大。故声波的衍射现象极为明显。
4.(多选)(2022·浙江绍兴市高二期中)如图所示是观察水波衍射的实验装置。AC和BD是两块挡板,AB是一个孔,O是波源。图中已画出波源所在区域波的传播情况,每两条相邻波纹(图中曲线)之间的距离表示一个波长,则关于波经过孔之后的传播情况,下列描述正确的是
A.能观察到明显的波的衍射现象
B.挡板前后波纹间距离相等
C.如果将孔AB扩大,可以观察到更明显的衍射现象
D.如果孔的大小不变,使波源频率增大,能观察到更明显的衍射现象
√
√
5.(2023·安徽安庆市高二检测)图中S为在水面上振动的波源,M、N是水面上的两块挡板,其中M板可以上下移动,两板中间有一狭缝,此时测得A处水没有振动,为使A处水也能发生振动,可采用的方法是
A.使波源的频率增大
B.使波源的振幅增大
C.向上移动M
D.向下移动M
√
波的干涉和衍射
波的叠加原理
波的衍射现象
波的干涉现象
波的独立传播性
波的叠加原理
保持各自原有的运动特征
各波列位移的矢量和
定义:振动加强和减弱区相互间隔,稳定分布
条件:频率和振动方向相同的波
图样特征:加强区波程差波长等于整数倍,减弱波程差等于区半波长奇数倍。
波的重要特征之一
定义:波绕过障碍物或通过孔隙继续传播的现象
明显衍射条件:障碍物或狭缝跟波长相差不大,或者比波长更小。
波特有的现象
第3章 机械波
3.3 波的干涉和衍射
时常会看到这样的现象:
几列水波相遇时,波形会发生变化,
水波脱离接触,又会恢复原来的形态。
为什么产生这样的现象呢?
1.如图所示,两列同相的波相遇前(①)、相遇中(②、③、④)、相遇后(⑤)的情景:
(1)比较两列波相遇前(①)与相遇后(⑤)的波形有什么关系?
两列波相遇前、相遇后的波形各自相同。
两列同相波叠加,振动加强、振幅增大。
(2)观察两列同相波的相遇中(②、③、④),振动是加强还是减弱的?振幅是增大还是减小的?
2.如图所示,两列反相的波相遇前(①)、相遇中(②、③)、相遇后(④)的情景:
(1)比较两列波相遇前(①)与相遇后(④)的波形有什么关系?
两列波相遇前、相遇后的波形各自相同。
(2)观察两列反相波的相遇中(②、③),振动是加强还是减弱的?振幅是增大还是减小的?
两列反相波的叠加,振动减弱,振幅减小。
[梳理与总结]
1.波的独立传播性
几列波在介质中传播,相遇后
。
仍能保持各自原有的运动特征(波长、频率、振幅等)不变并继续传播
2.波的叠加原理
在几列波相遇的区域里,介质中的质点同时参加相遇的波列的振动,质点的位移等于 。
相遇波列单独存在时在该处引起的位移的矢量和
声波在相互交错、叠加后互不影响,仍保持原来的性质向前传播。这种现象体现了波传播时具有独立性。
“风声、雨声、读书声,声声入耳”体现了波的什么性质?
(1)在两列波重叠的区域里,任何一个质点的位移都等于原来位移的2倍。( )
(2)两列波叠加时,质点的位移一定增大。( )
(3)只有频率相同的两列波才可以叠加。( )
(4)两列波相遇后各自的传播特点不会受到影响。( )
×
√
×
×
1.(多选)如图所示为两列相向传播且振幅、波长都相同的横波,它们相遇后,下列图像可能存在的是
√
√
波的叠加原理是波具有独立传播性的必然结果,由于总位移是各个位移的矢量和,所以叠加区域的质点的振幅可能增大,也可能减小。
(1)两列同相波叠加,振动加强,振幅增大。
(2)两列反相波叠加,振动减弱,振幅减小。
视频中手带动两个小球振动时,会产生振动方向、振动频率都相同的两列水波。观察这两列波叠加时的现象。
在振动的水面上,出现了一条条从两个波源中间扩散开的相对平静的区域和剧烈振动的区域,这两种区域相互间隔,并且出现的位置是固定的。
1.波的干涉的定义:振动频率和振动方向相同的两列波叠加后,振动加强和振动减弱的区域互相 、稳定分布的现象,称为波的干涉,形成的图样称为干涉图样。
2.产生干涉的条件: 和 相同的波。
间隔
频率
振动方向
3.干涉图样(如图)的特征
(1)加强区和减弱区的位置固定不变。
(2)加强区始终 ,减弱区始终 (加强区与减弱区不随时间变化)。
(3)加强区与减弱区互相 。
4.干涉现象是波的重要特征之一。
加强
减弱
间隔
1.振动加强点和振动减弱点的振幅有什么特点?能不能认为振动加强点的位移始终最大,振动减弱点的位移始终最小?为什么?
振动加强点:振动的振幅等于两列波振幅之和,A=A1+A2。振动减弱点:振动的振幅等于两列波振幅之差的绝对值,A=|A1-A2|。
不能,振动加强(减弱)点是指质点的振幅最大(小),而不是指振动的位移最大(小),因为位移是在时刻变化的,加强点和减弱点的位移均可以为零,只有发生干涉的两列波振幅大小相等,减弱点位移才始终为零。
2.如果两个波源频率不同,会不会出现振动总是加强与总是减弱的区域?为什么?
不会。如果两列波频率不同,在相遇点两列波的相位差会发生变化,不存在波峰总是与波峰相遇或波峰总是与波谷相遇的情况。
3.图中表示两列频率相同的横波相遇时某一时刻的情况,实线表示波峰,虚线表示波谷,此时M点是波峰与波峰相遇的点,是凸起最高的位置之一。
(1)半个周期后,图中六个点中,哪些点具有最大正向位移?哪些点具有负向最大位移?哪些点比较“平静”?
半个周期后,K、P点具有正向最大位移,M、Q具有负向最大位移,H、N点比较“平静”。
(2)随着时间的推移,原来M点这个凸起最高的位置在向哪个方向移动?是不是M质点在向那个方向迁移?M质点在哪个方向上运动?
凸起的最高点由M向P移动,M点并不随波迁移,而只在垂直于纸面的方向上运动。
(3)由图中时刻经过 时,M质点的位移有什么特点?
位移为0
2.(2023·福建漳州市高二月考)如图为振幅、频率相同的两列横波在t=0时刻相遇时形成的干涉图样,实线与虚线分别表示波峰和波谷,已知两列波的振幅均为5 cm,波速和波长均为1 m/s和0.4 m。下列说法正确的是
A.P点始终处于波谷
B.R、S两位置可以处于波谷状态
C.Q点在t=0.2 s时刻将处于波谷位置
D.从t=0到t=0.2 s的时间内,Q点通过的路程为10 cm
√
3.(2022·河北遵化第一中学高二月考)如图所示,S1、S2为两个振动情况完全相同的波源,两列波的波长都为λ,它们在均匀介质中产生干涉现象,S1、S2在空间中共形成了5个振动加强的区域,如图中实线所示。P是振动加强区域中的一点,由图可知
A.P点到两波源的距离差等于1.5λ
B.S1发出的波的传播速度大于S2发出的波的传播速度
C.P点此时刻振动最强,经过半个周期后,P点振动变为最弱
D.当一列波的波峰传到P点时,另一列波的波峰也一定传到P点
√
r1
r2
P
S1
S2
振动加强点和振动减弱点的判断
(1)条件判断法:振动频率相同、振动情况完全相同的两波叠加时,设点到两列波源的路程差为Δr,当Δr=|r2-r1|=kλ(k=0,1,2,…)
时为振动加强点;当Δr=|r2-r1|=(2k+1) (k=0,1,2,…)时为振动
减弱点。若两波源振动步调相反,则上述结论相反。
(2)现象判断法:若某点总是波峰与波峰或波谷与波谷相遇,该点为振动加强点,若总是波峰与波谷相遇,则为振动减弱点。
绕过障碍物传播
通过孔隙,传播范围变宽
波在传播过程中遇到障碍物时波的行为会发生什么变化?
1.定义
波绕过 或通过 继续传播的现象,称为波的衍射。
2.发生明显衍射现象的条件
障碍物或狭缝的尺寸跟 相差不大,或者比波长 。
3.一切波都能发生衍射,衍射是波 的现象。衍射现象只有“明显”与“不明显”之分。
障碍物
孔隙
波长
更小
特有
1.如果孔比波长大很多,波就不会发生衍射现象,这种说法对吗?
不对,一切波都能发生衍射,衍射是波特有的现象。孔比波长大很多时,衍射现象依然存在,只是无法观察到明显的衍射现象。
2.如果孔比波长小很多,一定能观察到明显的衍射现象吗?
不一定,如果孔比波长小的太多,绕过障碍物的波的能量较弱,也不易观察到明显的衍射现象。
3.为什么声波容易发生明显衍射现象?
声波的波长为1.7 cm~17 m,与一般障碍物的尺寸相比差不多,或比其大。故声波的衍射现象极为明显。
4.(多选)(2022·浙江绍兴市高二期中)如图所示是观察水波衍射的实验装置。AC和BD是两块挡板,AB是一个孔,O是波源。图中已画出波源所在区域波的传播情况,每两条相邻波纹(图中曲线)之间的距离表示一个波长,则关于波经过孔之后的传播情况,下列描述正确的是
A.能观察到明显的波的衍射现象
B.挡板前后波纹间距离相等
C.如果将孔AB扩大,可以观察到更明显的衍射现象
D.如果孔的大小不变,使波源频率增大,能观察到更明显的衍射现象
√
√
5.(2023·安徽安庆市高二检测)图中S为在水面上振动的波源,M、N是水面上的两块挡板,其中M板可以上下移动,两板中间有一狭缝,此时测得A处水没有振动,为使A处水也能发生振动,可采用的方法是
A.使波源的频率增大
B.使波源的振幅增大
C.向上移动M
D.向下移动M
√
波的干涉和衍射
波的叠加原理
波的衍射现象
波的干涉现象
波的独立传播性
波的叠加原理
保持各自原有的运动特征
各波列位移的矢量和
定义:振动加强和减弱区相互间隔,稳定分布
条件:频率和振动方向相同的波
图样特征:加强区波程差波长等于整数倍,减弱波程差等于区半波长奇数倍。
波的重要特征之一
定义:波绕过障碍物或通过孔隙继续传播的现象
明显衍射条件:障碍物或狭缝跟波长相差不大,或者比波长更小。
波特有的现象
同课章节目录
- 第1章 动量及其守恒定律
- 第1节 动量和动量定理
- 第2节 动量守恒定律及其应用
- 第3节 科学验证:动量守恒定律
- 第4节 弹性碰撞与非弹性碰撞
- 第2章 机械振动
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 科学测量:用单摆测量重力加速度
- 第5节 生活中的振动
- 第3章 机械波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第4章 光的折射和全反射
- 第1节 光的折射
- 第2节 科学测量:玻璃的折射率
- 第3节 光的全反射
- 第4节 光导纤维及其应用
- 第5章 光的干涉、衍射和偏振
- 第1节 光的干涉
- 第2节 科学测量:用双缝干涉测光的波长
- 第3节 光的衍射
- 第4节 光的偏振
- 第5节 激光与全息照相
