2.1 简谐运动 课件 高中物理鲁科版(2019)选择性必修一(共28张PPT)
文档属性
| 名称 | 2.1 简谐运动 课件 高中物理鲁科版(2019)选择性必修一(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 14.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-10-11 21:57:39 | ||
图片预览








文档简介
(共28张PPT)
第二章 机械振动
2.1 简谐运动
1
树叶来回摆动
秋千来回荡起
这些物体的运动有什么共同特点
如何研究这类运动呢
机械振动
1.机械振动:物体(或物体的某一部分)在某一位置附近的 运动称为机械振动,简称振动。
2.平衡位置:物体原来静止时的位置,即上述定义中的“某一位置”。
往复
振动的音叉
抖动的蜜蜂翅膀
振动的琴弦
一切发声的物体都在振动。机械振动是一种常见的运动。
机械振动是如何产生的?
演奏前,琴弦所受合力为0, 静止于平衡位置。演奏时拨动琴弦,使其偏离平衡位置。由于形变,琴弦产生一个指向平衡位置的弹力。
只要琴弦偏离平衡位置,它总会受到指向平衡位置的弹力。这种总是指向平衡位置的力称为回复力。
正是回复力的作用,使琴弦来回振动。
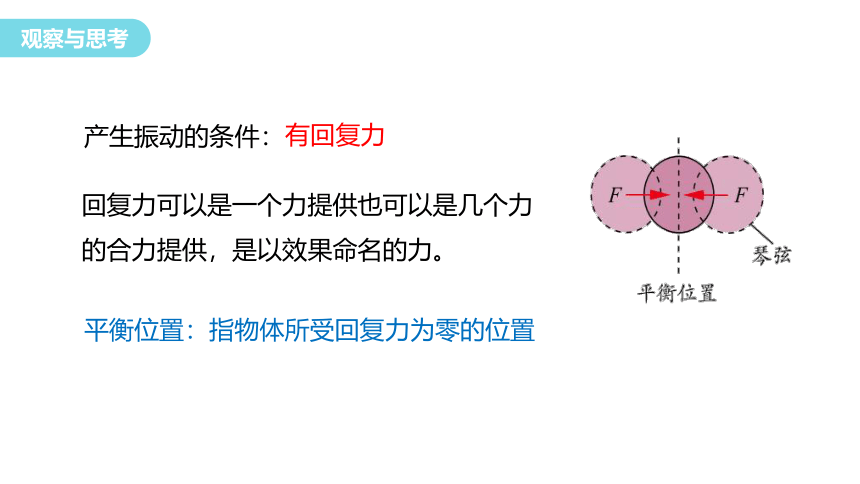
产生振动的条件:
回复力可以是一个力提供也可以是几个力的合力提供,是以效果命名的力。
平衡位置:指物体所受回复力为零的位置
有回复力
3.回复力
(1)定义:振动物体所受的总是指向 的力。
(2)方向:总是指向 。
(3)作用效果:使物体总是在平衡位置附近振动。
(4)来源:回复力可由振动物体受到的 来提供,也可由振动物体受到的几个力的 来提供。回复力为 的位置即平衡位置。
机械振动
平衡位置
平衡位置
某一个力
合力
0
滑板运动非常有趣。如图所示,某同学踩着滑板在弧形滑道的内壁来回滑行。滑板的这种运动可视为振动吗?若可以,它的平衡位置在哪里?
可以,平衡位置在弧形滑道的最低点。
(1)平衡位置即速度为零时的位置。( )
(2)机械振动是匀速直线运动。( )
(3)机械振动是物体在平衡位置附近所做的往复运动。( )
×
√
×
1.下列日常生活常见的情形中,不属于机械振动的是
A水中浮标上下浮动
B.秋千的摆动
C.琴弦的振动
D.表针沿表盘转动
√
弹簧振子是一种理想模型。弹簧一端固定,另一端连接一个可视为质点的物体,不计弹簧质量,物体置于光滑水平面上,这样构成的振动系统称为弹簧振子。
弹簧振子在运动方向上只受弹簧弹力作用。
如图(a),物体处于平衡位置O 时,弹簧为原长,物体所受的弹力为 0;
如图(b),将物体向右拉至B后由静止释放,物体将如何运动 各物理量如何变化
由于弹簧被拉长,物体受到向左指向平衡位置的弹力,向左加速运动,弹力减小,加速度减小,但速度增加。
(a)
(b)
如图(c),物块到达平衡位置O处会停止运动吗?
此后,在弹力的作用下,物体改变运动方向,由位置C返回位置B,……这样在平衡位置附近往复运动,形成振动。
物体所受弹簧的弹力提供了回复力
不会。此时物体所受弹力为虽然为 0, 但速度达到最大,由于惯性,会继续向左运动并挤压弹簧。
物体越过平衡位置向左将如何运动 各物理量如何变化
由于弹簧被压缩,物体受到向右指向平衡位置的弹力,向左减速运动,弹力增大,加速度增大,速度一直减小到0。如图(d)。
v
(c)
(d)
如图(a),取平衡位置O为 x 轴的原点,向右为 x 轴的正方向。
如图(b) , (c) ,回复力方向始终与位移的方向相反
根据胡克定律,回复力大小与位移的大小成正比
x
x
F=-kx
弹簧振子
(1)定义:弹簧一端固定,另一端连接一个可视为质点的物体,不计 ,物体置于 上,这样构成的振动系统称为弹簧振子。弹簧振子是一种理想模型。
(2)水平方向弹簧振子的回复力:
①来源:由物体所受弹簧的弹力提供。
②大小及方向: 。
其中k是弹簧的 ,x是物体相对平衡位置的 ,负号表示力与位移的方向 。
弹簧质量
光滑水平面
劲度系数
相反
位移
F=-kx
简谐振动
(1)定义:物体所受回复力的大小与位移大小成 ,方向总是与位移方向 的运动称为简谐运动。
(2)运动学特征:,即简谐运动的加速度的大小与位移大小成 ,方向与位移方向 。
(3)弹簧振子能量特征:只有弹簧的弹力做功,系统的 和 相互转换,机械能守恒。
正比
相反
动能
弹性势能
正比
相反
1.在劲度系数为k,原长为L0的固定于一点的弹簧下端挂一所受重力为G的小球,释放后小球做上下振动,弹簧始终在弹性限度内,不计空气阻力,小球的振动是简谐运动吗?如果是,什么力充当回复力?
规定向下为正方向,在平衡位置b点,有G=kx0,小球在c点受到的弹力大小为F′=k(x0+x),此时小球偏离平衡位置的位移为x,小球在c点的回复力F=G-F′=G-k(x0+x)=G-kx-kx0=-kx,回复力满足F=-kx,是简谐运动。弹簧弹力和重力的合力充当回复力。
2.简谐运动的回复力公式F=-kx中的k就是弹簧的劲度系数吗?以图中质量为m木块的运动为例分析(水平面光滑,两物体均做简谐运动且保持相对静止)。
把两个物体看成一个整体,他们的回复力由弹簧弹力提供,而质量为m的木块做简谐运动的回复力由静摩擦力f提供,由牛顿第二定律k0x=(m+M)a,f=ma,得,其中比例系数k和弹簧的劲度系数k0不同。简谐运动的回复力公式中,k是比例系数,不一定是弹簧的劲度系数,其值由振动系统决定。
(1)弹簧振子是一种理想化的模型。( )
(2)在F=-kx中,负号表示方向,不表示大小。( )
(3)弹簧振子的加速度方向一定与位移相同。( )
×
√
√
2.(多选)如图所示,质量为m的物体系在两轻质弹簧之间,弹簧劲度系数分别为k1和k2,且k1=k,k2=2k,两弹簧均处于自然状态。现向右拉动物体,然后释放,物体在B、C间振动,O为平衡位置(不计摩擦阻力),则下列判断正确的是
A.物体做简谐运动,OC=OB
B.物体做简谐运动,OC≠OB
C.回复力F=-kx
D.回复力F=-3kx
√
√
3.如图所示,倾角为α的斜面体(斜面光滑且足够长)固定在水平地面上,斜面顶端与劲度系数为k、自然长度为L的轻质弹簧相连,弹簧的另一端连接着质量为m的物块。压缩弹簧使其长度为时将物块由静止开始释放(物块做简谐运动),重力加速度为g。
(1)求物块处于平衡位置时弹簧的长度;
(2)选物块的平衡位置为坐标原点,沿斜面向下为正方向建立坐标系,用x表示物块相对于平衡位置的位移,证明物块做简谐运动。(已知做简谐运动的物体所受的回复力满足F=-kx)
判断一个振动是否为简谐运动的方法
1.动力学方法:对物体进行受力分析,物体所受的回复力满足F=-kx,即可判断物体做简谐运动。
2.运动学方法:根据牛顿第二定律或运动学知识,求解物体的加速度,如果满足,即可判断物体做简谐运动。
一小球做简谐运动,相继经过如图所示的位置。试根据图示,判断小球在此振动过程中的位移、回复力、加速度、速度、动能和弹簧的弹性势能分别是如何变化的,填入表中。然后找出以上各物理量分别在小球运动至何处时最大,何处时最小。
C O B
位移x、回复力F、加速度a、弹性势能最大处: ;最小处: ;
速度v、动能Ek最大处: ;最小处: 。
小球位置 O→B B→O O→C C→O
位移x
回复力F
加速度a
速度v
动能Ek
弹性势能Ep
增大
增大
增大
减小
增大
减小
减小
减小
减小
减小
增大
增大
增大
增大
增大
增大
减小
减小
减小
减小
减小
减小
增大
增大
B 处或C 处
B 处或C 处
O 处
O 处
4.(2023·吉林白山市高二期末)如图所示,光滑水平面上的弹簧振子以O点为平衡位置在B、C两点间做简谐运动,取向左为正方向,则振子从O点运动到B点的过程中
A.位移不断减小
B.加速度不断减小
C.位移方向与加速度方向始终相同
D.速度减小,弹性势能增大
√
5.一弹簧振子做简谐运动,下列说法正确的是
A.若位移为负值,则速度一定为正值,加速度也一定为正值
B.物体每次经过平衡位置时,加速度相同,速度也一定相同
C.物体每次通过同一位置时,其速度不一定相同,但加速度一定相同
D.物体在平衡位置两侧对称的位置上,其速度、位移都反向
√
1.当小球远离平衡位置过程中,位移增大,回复力、加速度和势能增大,速度和动能减小;当小球衡位置过程中,位移减小,回复力、加速度和势能减小,速度和动能增大。
2.简谐运动中的物体距平衡位置最远处,F、a、Ep最大,Ek=0;在平衡位置处,F=0,a=0,Ep最小,Ek最大。
3.两个“方向变化”的转折点
(1)平衡位置是位移方向、回复力方向和加速度方向变化的转折点。
(2)物体距平衡位置最远处是速度方向变化的转折点。
简谐运动
一
机械振动
二
简谐运动及其特征
三
简谐运动过程中各物理量的变化
平衡位置:在振动方向所受合力为0
回复力:始终指向平衡位置,振动产生的原因.
弹簧振子:理想化模型,振动过程能量守恒.
判定简谐运动的方法
动力学:F=-kx
运动学:
以位移为纽带
速度
加速度
动能
势能
第二章 机械振动
2.1 简谐运动
1
树叶来回摆动
秋千来回荡起
这些物体的运动有什么共同特点
如何研究这类运动呢
机械振动
1.机械振动:物体(或物体的某一部分)在某一位置附近的 运动称为机械振动,简称振动。
2.平衡位置:物体原来静止时的位置,即上述定义中的“某一位置”。
往复
振动的音叉
抖动的蜜蜂翅膀
振动的琴弦
一切发声的物体都在振动。机械振动是一种常见的运动。
机械振动是如何产生的?
演奏前,琴弦所受合力为0, 静止于平衡位置。演奏时拨动琴弦,使其偏离平衡位置。由于形变,琴弦产生一个指向平衡位置的弹力。
只要琴弦偏离平衡位置,它总会受到指向平衡位置的弹力。这种总是指向平衡位置的力称为回复力。
正是回复力的作用,使琴弦来回振动。
产生振动的条件:
回复力可以是一个力提供也可以是几个力的合力提供,是以效果命名的力。
平衡位置:指物体所受回复力为零的位置
有回复力
3.回复力
(1)定义:振动物体所受的总是指向 的力。
(2)方向:总是指向 。
(3)作用效果:使物体总是在平衡位置附近振动。
(4)来源:回复力可由振动物体受到的 来提供,也可由振动物体受到的几个力的 来提供。回复力为 的位置即平衡位置。
机械振动
平衡位置
平衡位置
某一个力
合力
0
滑板运动非常有趣。如图所示,某同学踩着滑板在弧形滑道的内壁来回滑行。滑板的这种运动可视为振动吗?若可以,它的平衡位置在哪里?
可以,平衡位置在弧形滑道的最低点。
(1)平衡位置即速度为零时的位置。( )
(2)机械振动是匀速直线运动。( )
(3)机械振动是物体在平衡位置附近所做的往复运动。( )
×
√
×
1.下列日常生活常见的情形中,不属于机械振动的是
A水中浮标上下浮动
B.秋千的摆动
C.琴弦的振动
D.表针沿表盘转动
√
弹簧振子是一种理想模型。弹簧一端固定,另一端连接一个可视为质点的物体,不计弹簧质量,物体置于光滑水平面上,这样构成的振动系统称为弹簧振子。
弹簧振子在运动方向上只受弹簧弹力作用。
如图(a),物体处于平衡位置O 时,弹簧为原长,物体所受的弹力为 0;
如图(b),将物体向右拉至B后由静止释放,物体将如何运动 各物理量如何变化
由于弹簧被拉长,物体受到向左指向平衡位置的弹力,向左加速运动,弹力减小,加速度减小,但速度增加。
(a)
(b)
如图(c),物块到达平衡位置O处会停止运动吗?
此后,在弹力的作用下,物体改变运动方向,由位置C返回位置B,……这样在平衡位置附近往复运动,形成振动。
物体所受弹簧的弹力提供了回复力
不会。此时物体所受弹力为虽然为 0, 但速度达到最大,由于惯性,会继续向左运动并挤压弹簧。
物体越过平衡位置向左将如何运动 各物理量如何变化
由于弹簧被压缩,物体受到向右指向平衡位置的弹力,向左减速运动,弹力增大,加速度增大,速度一直减小到0。如图(d)。
v
(c)
(d)
如图(a),取平衡位置O为 x 轴的原点,向右为 x 轴的正方向。
如图(b) , (c) ,回复力方向始终与位移的方向相反
根据胡克定律,回复力大小与位移的大小成正比
x
x
F=-kx
弹簧振子
(1)定义:弹簧一端固定,另一端连接一个可视为质点的物体,不计 ,物体置于 上,这样构成的振动系统称为弹簧振子。弹簧振子是一种理想模型。
(2)水平方向弹簧振子的回复力:
①来源:由物体所受弹簧的弹力提供。
②大小及方向: 。
其中k是弹簧的 ,x是物体相对平衡位置的 ,负号表示力与位移的方向 。
弹簧质量
光滑水平面
劲度系数
相反
位移
F=-kx
简谐振动
(1)定义:物体所受回复力的大小与位移大小成 ,方向总是与位移方向 的运动称为简谐运动。
(2)运动学特征:,即简谐运动的加速度的大小与位移大小成 ,方向与位移方向 。
(3)弹簧振子能量特征:只有弹簧的弹力做功,系统的 和 相互转换,机械能守恒。
正比
相反
动能
弹性势能
正比
相反
1.在劲度系数为k,原长为L0的固定于一点的弹簧下端挂一所受重力为G的小球,释放后小球做上下振动,弹簧始终在弹性限度内,不计空气阻力,小球的振动是简谐运动吗?如果是,什么力充当回复力?
规定向下为正方向,在平衡位置b点,有G=kx0,小球在c点受到的弹力大小为F′=k(x0+x),此时小球偏离平衡位置的位移为x,小球在c点的回复力F=G-F′=G-k(x0+x)=G-kx-kx0=-kx,回复力满足F=-kx,是简谐运动。弹簧弹力和重力的合力充当回复力。
2.简谐运动的回复力公式F=-kx中的k就是弹簧的劲度系数吗?以图中质量为m木块的运动为例分析(水平面光滑,两物体均做简谐运动且保持相对静止)。
把两个物体看成一个整体,他们的回复力由弹簧弹力提供,而质量为m的木块做简谐运动的回复力由静摩擦力f提供,由牛顿第二定律k0x=(m+M)a,f=ma,得,其中比例系数k和弹簧的劲度系数k0不同。简谐运动的回复力公式中,k是比例系数,不一定是弹簧的劲度系数,其值由振动系统决定。
(1)弹簧振子是一种理想化的模型。( )
(2)在F=-kx中,负号表示方向,不表示大小。( )
(3)弹簧振子的加速度方向一定与位移相同。( )
×
√
√
2.(多选)如图所示,质量为m的物体系在两轻质弹簧之间,弹簧劲度系数分别为k1和k2,且k1=k,k2=2k,两弹簧均处于自然状态。现向右拉动物体,然后释放,物体在B、C间振动,O为平衡位置(不计摩擦阻力),则下列判断正确的是
A.物体做简谐运动,OC=OB
B.物体做简谐运动,OC≠OB
C.回复力F=-kx
D.回复力F=-3kx
√
√
3.如图所示,倾角为α的斜面体(斜面光滑且足够长)固定在水平地面上,斜面顶端与劲度系数为k、自然长度为L的轻质弹簧相连,弹簧的另一端连接着质量为m的物块。压缩弹簧使其长度为时将物块由静止开始释放(物块做简谐运动),重力加速度为g。
(1)求物块处于平衡位置时弹簧的长度;
(2)选物块的平衡位置为坐标原点,沿斜面向下为正方向建立坐标系,用x表示物块相对于平衡位置的位移,证明物块做简谐运动。(已知做简谐运动的物体所受的回复力满足F=-kx)
判断一个振动是否为简谐运动的方法
1.动力学方法:对物体进行受力分析,物体所受的回复力满足F=-kx,即可判断物体做简谐运动。
2.运动学方法:根据牛顿第二定律或运动学知识,求解物体的加速度,如果满足,即可判断物体做简谐运动。
一小球做简谐运动,相继经过如图所示的位置。试根据图示,判断小球在此振动过程中的位移、回复力、加速度、速度、动能和弹簧的弹性势能分别是如何变化的,填入表中。然后找出以上各物理量分别在小球运动至何处时最大,何处时最小。
C O B
位移x、回复力F、加速度a、弹性势能最大处: ;最小处: ;
速度v、动能Ek最大处: ;最小处: 。
小球位置 O→B B→O O→C C→O
位移x
回复力F
加速度a
速度v
动能Ek
弹性势能Ep
增大
增大
增大
减小
增大
减小
减小
减小
减小
减小
增大
增大
增大
增大
增大
增大
减小
减小
减小
减小
减小
减小
增大
增大
B 处或C 处
B 处或C 处
O 处
O 处
4.(2023·吉林白山市高二期末)如图所示,光滑水平面上的弹簧振子以O点为平衡位置在B、C两点间做简谐运动,取向左为正方向,则振子从O点运动到B点的过程中
A.位移不断减小
B.加速度不断减小
C.位移方向与加速度方向始终相同
D.速度减小,弹性势能增大
√
5.一弹簧振子做简谐运动,下列说法正确的是
A.若位移为负值,则速度一定为正值,加速度也一定为正值
B.物体每次经过平衡位置时,加速度相同,速度也一定相同
C.物体每次通过同一位置时,其速度不一定相同,但加速度一定相同
D.物体在平衡位置两侧对称的位置上,其速度、位移都反向
√
1.当小球远离平衡位置过程中,位移增大,回复力、加速度和势能增大,速度和动能减小;当小球衡位置过程中,位移减小,回复力、加速度和势能减小,速度和动能增大。
2.简谐运动中的物体距平衡位置最远处,F、a、Ep最大,Ek=0;在平衡位置处,F=0,a=0,Ep最小,Ek最大。
3.两个“方向变化”的转折点
(1)平衡位置是位移方向、回复力方向和加速度方向变化的转折点。
(2)物体距平衡位置最远处是速度方向变化的转折点。
简谐运动
一
机械振动
二
简谐运动及其特征
三
简谐运动过程中各物理量的变化
平衡位置:在振动方向所受合力为0
回复力:始终指向平衡位置,振动产生的原因.
弹簧振子:理想化模型,振动过程能量守恒.
判定简谐运动的方法
动力学:F=-kx
运动学:
以位移为纽带
速度
加速度
动能
势能
同课章节目录
- 第1章 动量及其守恒定律
- 第1节 动量和动量定理
- 第2节 动量守恒定律及其应用
- 第3节 科学验证:动量守恒定律
- 第4节 弹性碰撞与非弹性碰撞
- 第2章 机械振动
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 科学测量:用单摆测量重力加速度
- 第5节 生活中的振动
- 第3章 机械波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第4章 光的折射和全反射
- 第1节 光的折射
- 第2节 科学测量:玻璃的折射率
- 第3节 光的全反射
- 第4节 光导纤维及其应用
- 第5章 光的干涉、衍射和偏振
- 第1节 光的干涉
- 第2节 科学测量:用双缝干涉测光的波长
- 第3节 光的衍射
- 第4节 光的偏振
- 第5节 激光与全息照相
