2.5 生活中的振动 课件 高中物理鲁科版(2019)选择性必修一(共33张PPT)
文档属性
| 名称 | 2.5 生活中的振动 课件 高中物理鲁科版(2019)选择性必修一(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 126.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览











文档简介
(共33张PPT)
第二章 机械振动
2.5 生活中的振动
弹簧振子
单摆
理想化模型
简谐振动
x=Asinωt
◆简谐运动是等幅振动,对于给定的振动系统都有各自固有周期(或固有频率)。
◆简谐运动中动能和势能发生相互转化,总机械能保持不变,即机械能守恒。
◆振动系统的总机械能与振幅有关,振幅越大,总机械能越大。
振动方向上
只受回复力
实际生活中的各类振动,往往存在振动阻力或其他外力的影响。这种情况下,物体的振动有什么特点呢?
阻尼振动
水中的弹簧振子、汽车上的减震器之所以不能持续振动,是因为它们在振动过程中受到阻力,使振动逐渐减弱。
如图所示,弹簧振子在水中不能持续振动,汽车上的减震器能让汽车的振动很快停下来,它们为什么不能持续振动?这些振动有什么特点?
汽车上的减震器
[梳理与总结]
1.自由振动:
对于一个振动系统,若振动物体偏离平衡位置后,仅在 作用下振动,这种振动就是自由振动。
2.阻尼振动
(1)定义:
阻尼振动是指振幅 的振动。
回复力
不断减小
振动过程中由于存在 ,振动物体需要不断 ,系统的机械能不断 ,导致振幅不断减小。
(2)产生的原因 :
(3)图像:
如图所示,振幅 ,最后停止振动。
阻力 克服阻力做功
减小
逐渐减小
1.阻尼振动中,在振幅逐渐减小的过程中,振子的频率如何变化?
不变,振子的频率与振幅无关。
2.在什么情况下可以把实际的振动看作简谐运动?
当阻力很小时,在不太长的时间内看不出振幅有明显的减小,则可以把它当作简谐运动来处理。
(1)做阻尼振动的物体因克服阻力做功,它的机械能逐渐减小。( )
(2)阻力越大,物体的振幅减小的越快。( )
(3)阻尼振动振幅逐渐减小时,其固有频率也逐渐减小。( )
×
√
√
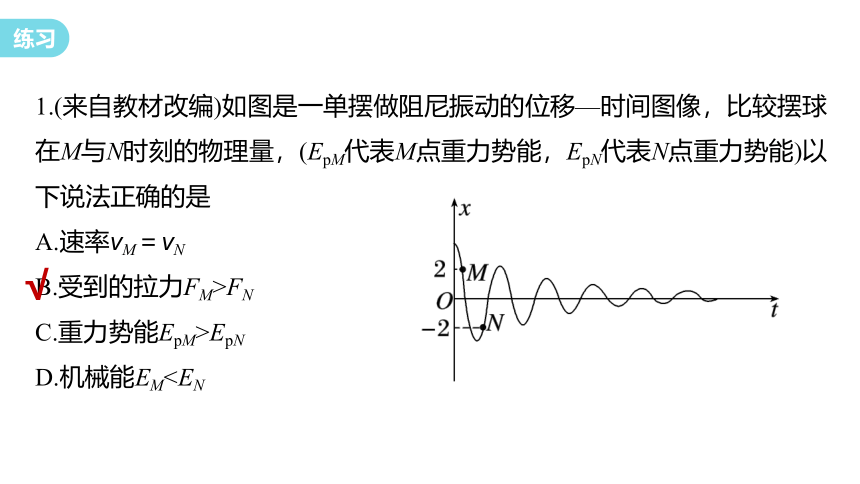
1.(来自教材改编)如图是一单摆做阻尼振动的位移—时间图像,比较摆球在M与N时刻的物理量,(EpM代表M点重力势能,EpN代表N点重力势能)以下说法正确的是
A.速率vM=vN
B.受到的拉力FM>FN
C.重力势能EpM>EpN
D.机械能EM√
受迫振动与共振
在实际振动过程中,阻力总是客观存在的。只能设法减小而不能全面消除。所以实际的振动一定是阻尼振动,最终会停下来。
用什么办法才能获得稳定的振动呢
1.受迫振动
(1)驱动力:
为了获得稳定的振动,通常需要给振动物体施加一个 ,这种 称为驱动力。
(2)受迫振动:在 作用下产生的振动。
如为使秋千稳定荡漾,定期推动秋千的力;为使振针稳定打点,带动振片振动的电磁力(交流电产生的周期性变化的力);●●● ●●●
秋千的稳定荡漾;打点计时器振片稳定的振动;●●● ●●●
周期性的外力
周期性的外力
周期性外力
(3)受迫振动的周期或频率
①安装好实验装置(如图),用力拉弹簧振子到合适位置,释放振子,测量振子的周期T1,一段时间后振子停止运动;说明振子运动时存在阻力。(阻尼振动)
②匀速转动摇把,摇把对弹簧 振子施加周期性的驱动力,使振子做受迫振动,记录摇把的周期T2,振子振动的周期T3。
物体做受迫振动时,振动稳定后的周期(或频率)总等于 的周期(或频率),与物体的固有周期(或固有频率)无关。
③改变摇把的转速,重复步骤②。将弹簧振子做受迫振动的周期与弹簧振子的固有周期、摇把转动的周期进行比较,找出弹簧振子做受迫振动的周期变化规律。
驱动力
在上述实验中, 当摇把转动的周期越接近弹簧振子的固有周期时,弹簧振子的振幅有什么变化
弹簧振子做受迫振动的振幅越大。
物体做受迫振动时, 驱动力的周期会对振幅产生怎样的影响?
当驱动力的周期(或频率)与物体的固有周期(或固有频率)相等时,受迫振动的 达到最大,这种现象称为共振。
(1)定义:
(2)条件:
(3)共振曲线:受迫振动的振幅与驱动力频率的关系如图所示。
f=f固时发生共振;
f>f固或ff与f固相差越小,振幅越大。
驱动力的周期(或频率) 物体的固有周期(或固有频率)。
横轴:表示驱动力的频率
纵轴:表示受迫振动的振幅
2.共振
振幅
等于
洗衣机在衣服脱水完毕关闭电源后,脱水桶还要转动一会才能停下来。在关闭电源后,发现洗衣机先振动得比较弱,有一阵子振动得很剧烈,然后振动慢慢减弱直至停下来。
(1)开始时,洗衣机为什么振动比较弱?
开始时,脱水桶转动的频率远高于洗衣机的固有频率,振幅较小,振动比较弱。
(2)期间剧烈振动的原因是什么?
当洗衣机脱水桶转动的频率等于洗衣机的固有频率时发生共振,振动剧烈。
2.(多选)下列说法中正确的是
A.有阻力的振动称为受迫振动
B.物体振动时受到外力作用,它的振动就是受迫振动
C.物体在周期性外力作用下的振动称为受迫振动
D.物体在周期性外力作用下振动,它的振动频率最终等于驱动力频率
√
√
3.如图所示的装置中,弹簧振子的固有频率的是4 Hz,现匀速转动把手,给弹簧振子以周期性的驱动力,测得弹簧振子振动达到稳定时的频率为1 Hz,则把手转动的频率为
A.1 Hz B.3 Hz
C.4 Hz D.5 Hz
√
4.(多选)(来自教材)如图所示是一弹簧振子做受迫振动时的振幅与驱动力频率的关系,由图可知
A.假如让振子自由振动,它的频率为f2
B.驱动力的频率为f2时,振子处于共振状态
C.驱动力的频率为f3时,振子的振动频率为f3
D.振子做自由振动时,频率可以为f1、f2和f3
√
√
√
5.(多选)(2023·湖南长沙市高二期末)如图所示,A、B、C、D四个单摆的摆长分别为L、2L、L、 ,摆球的质量分别为2m、2m、m、 ,四个单摆静止地悬挂在一根水平细线上。现让A振动起来,通过水平细线迫使B、C、D也振动起来,则下列说法正确的是
A.B、C、D中B的摆长最长,振幅最大
B.B、C、D中C的振幅最大
C.B、C、D中因D的质量最小,故其振幅是最大的
D.A、B、C、D四个单摆的周期均相同
√
√
共振的应用与防止
1.共振的应用
在应用共振时,应使驱动力频率接近或等于振动系统的 ,振动将更剧烈。
通过调节振动锤头的振动频率, 使其等于或接近水泥路面的固有频率,从而使锤头下的水泥路面因局部范围产生共振而被击碎。这种路面共振破碎机具有破碎效率高、 破碎深度大等特点。
固有频率
把某一频率的音叉插在一端开口的共鸣箱上,当敲击音叉使它振动时, 箱内的空气柱能产生共振,发岀较响的声音, 这种现象称为共鸣。共鸣是一种声共振现象。
2.共振的防止
在防止共振时,驱动力频率与系统的 相差越大越好。
轮船航行时,常会受到周期性的海浪冲击而摆动,如果海浪冲击力的频率与轮船的固有频率相同,就会发生共振,轮船可能会剧烈摇摆甚至倾覆。
通过改变轮船的航向和速率,使海浪冲击力的频率与轮船的固有频率相差很大,以此防止共振发生。
固有频率
1831年,一队骑兵通过曼彻斯特附近的一座便桥时,由于马蹄节奏整齐,桥梁发生共振而断裂。
集体列队经过桥梁时要便步走,以防对桥梁形成的周期性驱动力使桥梁发生共振。
生活中的共振现象
声音震碎玻璃杯
大桥的垮塌
鱼洗
振动的沙子
1.荡过秋千的人都有这种经验:轻推一下使它微微摆动后,只要按照它的固有频率周期性地施加推力,尽管每次的推力都很小,经过一段时间,秋千也会荡的很高。这是为什么?
若周期性的驱动力给系统补充的能量与系统因阻尼振动消耗的能量相等,那么秋千振动的振幅是否变化?它能否看成简谐运动?
这是因为周期性的驱动力给系统补充的能量比系统因阻尼振动消耗的能量多。
做等幅振动,但此振动不是简谐运动。
2.唐朝洛阳有个和尚喜欢弹拨一种叫磬的乐器,如图所示。奇怪的是磬在无人弹拨时经常自发鸣响,无缘无故地发生嗡嗡的声音,磬无故而鸣,使和尚大为惊奇,渐渐由惊而疑,由疑而怯,以为是妖孽作怪,结果忧虑成疾,病倒在床。一天,和尚向前来探望他的朋友诉说了内心的忧虑,正在说话时,寺院里的钟声响了,说来奇怪,磬也发出了嗡嗡的响声。和尚的朋友明白了原因,悄悄用钢锉在磬上锉了几处,从此之后,磬再也不会无故发声了。和尚以为妖怪已被赶走,心事顿消,病也不治而愈。
(1)磬为什么会不敲自鸣呢?
磬不敲自鸣是共振现象,磬的固有频率和钟的频率一样,因此每当钟响时,引起磬的共振而发出嗡嗡之声。
(2)和尚的朋友悄悄用钢锉在磬上锉了几处之后,为什么磬再也不会无故发声?
和尚的朋友悄悄用钢锉在磬上锉了几处之后,改变了其固有频率,使其固有频率与钟的频率不再一致了,钟响时不会引起磬的共振而无故发声。
(1)做受迫振动的物体其频率由自身决定。( )
(2)驱动力的频率越大振动物体振幅越大。( )
(3)共振的条件是驱动力的频率等于物体的固有频率。( )
×
√
×
6.(多选)(2022·吉林长春二中月考)铺设铁轨时,每两根钢轨接缝处都必须留有一定的间隙,匀速运行的列车经过轨端接缝处时,车轮就会受到一次冲击。由于每一根钢轨长度相等,所以这个冲击力是周期性的,列车受到周期性的冲击做受迫振动。普通钢轨长为12.6 m,列车的固有周期为0.315 s。下列说法正确的是
A.列车的危险速率为40 m/s
B.列车过桥需要减速,是为了防止列车发生共振现象
C.列车运行的振动频率和列车的固有频率总是相等的
D.增加钢轨的长度有利于列车高速运行
√
√
生活中的振动
一
阻尼振动
二
受迫振动与共振
三
共振的应用防止
自由振动
阻尼振动
仅在回复力作用下的振动
定义
产生原因
图像
振幅不断减小
克服阻力做功,机械能减少。
周期(频率)不变
受迫振动
共振
驱动力
受迫振动
周期(频率)
周期性外力
在驱动力作用下的振动
总等于驱动力的周期(频率)
定义
条件
共振曲线
受迫振动的振幅最大
共振的应用
共振的防止
使f驱=f固或使f驱接近f固
使f驱远离f固
f驱=f固
第二章 机械振动
2.5 生活中的振动
弹簧振子
单摆
理想化模型
简谐振动
x=Asinωt
◆简谐运动是等幅振动,对于给定的振动系统都有各自固有周期(或固有频率)。
◆简谐运动中动能和势能发生相互转化,总机械能保持不变,即机械能守恒。
◆振动系统的总机械能与振幅有关,振幅越大,总机械能越大。
振动方向上
只受回复力
实际生活中的各类振动,往往存在振动阻力或其他外力的影响。这种情况下,物体的振动有什么特点呢?
阻尼振动
水中的弹簧振子、汽车上的减震器之所以不能持续振动,是因为它们在振动过程中受到阻力,使振动逐渐减弱。
如图所示,弹簧振子在水中不能持续振动,汽车上的减震器能让汽车的振动很快停下来,它们为什么不能持续振动?这些振动有什么特点?
汽车上的减震器
[梳理与总结]
1.自由振动:
对于一个振动系统,若振动物体偏离平衡位置后,仅在 作用下振动,这种振动就是自由振动。
2.阻尼振动
(1)定义:
阻尼振动是指振幅 的振动。
回复力
不断减小
振动过程中由于存在 ,振动物体需要不断 ,系统的机械能不断 ,导致振幅不断减小。
(2)产生的原因 :
(3)图像:
如图所示,振幅 ,最后停止振动。
阻力 克服阻力做功
减小
逐渐减小
1.阻尼振动中,在振幅逐渐减小的过程中,振子的频率如何变化?
不变,振子的频率与振幅无关。
2.在什么情况下可以把实际的振动看作简谐运动?
当阻力很小时,在不太长的时间内看不出振幅有明显的减小,则可以把它当作简谐运动来处理。
(1)做阻尼振动的物体因克服阻力做功,它的机械能逐渐减小。( )
(2)阻力越大,物体的振幅减小的越快。( )
(3)阻尼振动振幅逐渐减小时,其固有频率也逐渐减小。( )
×
√
√
1.(来自教材改编)如图是一单摆做阻尼振动的位移—时间图像,比较摆球在M与N时刻的物理量,(EpM代表M点重力势能,EpN代表N点重力势能)以下说法正确的是
A.速率vM=vN
B.受到的拉力FM>FN
C.重力势能EpM>EpN
D.机械能EM
受迫振动与共振
在实际振动过程中,阻力总是客观存在的。只能设法减小而不能全面消除。所以实际的振动一定是阻尼振动,最终会停下来。
用什么办法才能获得稳定的振动呢
1.受迫振动
(1)驱动力:
为了获得稳定的振动,通常需要给振动物体施加一个 ,这种 称为驱动力。
(2)受迫振动:在 作用下产生的振动。
如为使秋千稳定荡漾,定期推动秋千的力;为使振针稳定打点,带动振片振动的电磁力(交流电产生的周期性变化的力);●●● ●●●
秋千的稳定荡漾;打点计时器振片稳定的振动;●●● ●●●
周期性的外力
周期性的外力
周期性外力
(3)受迫振动的周期或频率
①安装好实验装置(如图),用力拉弹簧振子到合适位置,释放振子,测量振子的周期T1,一段时间后振子停止运动;说明振子运动时存在阻力。(阻尼振动)
②匀速转动摇把,摇把对弹簧 振子施加周期性的驱动力,使振子做受迫振动,记录摇把的周期T2,振子振动的周期T3。
物体做受迫振动时,振动稳定后的周期(或频率)总等于 的周期(或频率),与物体的固有周期(或固有频率)无关。
③改变摇把的转速,重复步骤②。将弹簧振子做受迫振动的周期与弹簧振子的固有周期、摇把转动的周期进行比较,找出弹簧振子做受迫振动的周期变化规律。
驱动力
在上述实验中, 当摇把转动的周期越接近弹簧振子的固有周期时,弹簧振子的振幅有什么变化
弹簧振子做受迫振动的振幅越大。
物体做受迫振动时, 驱动力的周期会对振幅产生怎样的影响?
当驱动力的周期(或频率)与物体的固有周期(或固有频率)相等时,受迫振动的 达到最大,这种现象称为共振。
(1)定义:
(2)条件:
(3)共振曲线:受迫振动的振幅与驱动力频率的关系如图所示。
f=f固时发生共振;
f>f固或f
驱动力的周期(或频率) 物体的固有周期(或固有频率)。
横轴:表示驱动力的频率
纵轴:表示受迫振动的振幅
2.共振
振幅
等于
洗衣机在衣服脱水完毕关闭电源后,脱水桶还要转动一会才能停下来。在关闭电源后,发现洗衣机先振动得比较弱,有一阵子振动得很剧烈,然后振动慢慢减弱直至停下来。
(1)开始时,洗衣机为什么振动比较弱?
开始时,脱水桶转动的频率远高于洗衣机的固有频率,振幅较小,振动比较弱。
(2)期间剧烈振动的原因是什么?
当洗衣机脱水桶转动的频率等于洗衣机的固有频率时发生共振,振动剧烈。
2.(多选)下列说法中正确的是
A.有阻力的振动称为受迫振动
B.物体振动时受到外力作用,它的振动就是受迫振动
C.物体在周期性外力作用下的振动称为受迫振动
D.物体在周期性外力作用下振动,它的振动频率最终等于驱动力频率
√
√
3.如图所示的装置中,弹簧振子的固有频率的是4 Hz,现匀速转动把手,给弹簧振子以周期性的驱动力,测得弹簧振子振动达到稳定时的频率为1 Hz,则把手转动的频率为
A.1 Hz B.3 Hz
C.4 Hz D.5 Hz
√
4.(多选)(来自教材)如图所示是一弹簧振子做受迫振动时的振幅与驱动力频率的关系,由图可知
A.假如让振子自由振动,它的频率为f2
B.驱动力的频率为f2时,振子处于共振状态
C.驱动力的频率为f3时,振子的振动频率为f3
D.振子做自由振动时,频率可以为f1、f2和f3
√
√
√
5.(多选)(2023·湖南长沙市高二期末)如图所示,A、B、C、D四个单摆的摆长分别为L、2L、L、 ,摆球的质量分别为2m、2m、m、 ,四个单摆静止地悬挂在一根水平细线上。现让A振动起来,通过水平细线迫使B、C、D也振动起来,则下列说法正确的是
A.B、C、D中B的摆长最长,振幅最大
B.B、C、D中C的振幅最大
C.B、C、D中因D的质量最小,故其振幅是最大的
D.A、B、C、D四个单摆的周期均相同
√
√
共振的应用与防止
1.共振的应用
在应用共振时,应使驱动力频率接近或等于振动系统的 ,振动将更剧烈。
通过调节振动锤头的振动频率, 使其等于或接近水泥路面的固有频率,从而使锤头下的水泥路面因局部范围产生共振而被击碎。这种路面共振破碎机具有破碎效率高、 破碎深度大等特点。
固有频率
把某一频率的音叉插在一端开口的共鸣箱上,当敲击音叉使它振动时, 箱内的空气柱能产生共振,发岀较响的声音, 这种现象称为共鸣。共鸣是一种声共振现象。
2.共振的防止
在防止共振时,驱动力频率与系统的 相差越大越好。
轮船航行时,常会受到周期性的海浪冲击而摆动,如果海浪冲击力的频率与轮船的固有频率相同,就会发生共振,轮船可能会剧烈摇摆甚至倾覆。
通过改变轮船的航向和速率,使海浪冲击力的频率与轮船的固有频率相差很大,以此防止共振发生。
固有频率
1831年,一队骑兵通过曼彻斯特附近的一座便桥时,由于马蹄节奏整齐,桥梁发生共振而断裂。
集体列队经过桥梁时要便步走,以防对桥梁形成的周期性驱动力使桥梁发生共振。
生活中的共振现象
声音震碎玻璃杯
大桥的垮塌
鱼洗
振动的沙子
1.荡过秋千的人都有这种经验:轻推一下使它微微摆动后,只要按照它的固有频率周期性地施加推力,尽管每次的推力都很小,经过一段时间,秋千也会荡的很高。这是为什么?
若周期性的驱动力给系统补充的能量与系统因阻尼振动消耗的能量相等,那么秋千振动的振幅是否变化?它能否看成简谐运动?
这是因为周期性的驱动力给系统补充的能量比系统因阻尼振动消耗的能量多。
做等幅振动,但此振动不是简谐运动。
2.唐朝洛阳有个和尚喜欢弹拨一种叫磬的乐器,如图所示。奇怪的是磬在无人弹拨时经常自发鸣响,无缘无故地发生嗡嗡的声音,磬无故而鸣,使和尚大为惊奇,渐渐由惊而疑,由疑而怯,以为是妖孽作怪,结果忧虑成疾,病倒在床。一天,和尚向前来探望他的朋友诉说了内心的忧虑,正在说话时,寺院里的钟声响了,说来奇怪,磬也发出了嗡嗡的响声。和尚的朋友明白了原因,悄悄用钢锉在磬上锉了几处,从此之后,磬再也不会无故发声了。和尚以为妖怪已被赶走,心事顿消,病也不治而愈。
(1)磬为什么会不敲自鸣呢?
磬不敲自鸣是共振现象,磬的固有频率和钟的频率一样,因此每当钟响时,引起磬的共振而发出嗡嗡之声。
(2)和尚的朋友悄悄用钢锉在磬上锉了几处之后,为什么磬再也不会无故发声?
和尚的朋友悄悄用钢锉在磬上锉了几处之后,改变了其固有频率,使其固有频率与钟的频率不再一致了,钟响时不会引起磬的共振而无故发声。
(1)做受迫振动的物体其频率由自身决定。( )
(2)驱动力的频率越大振动物体振幅越大。( )
(3)共振的条件是驱动力的频率等于物体的固有频率。( )
×
√
×
6.(多选)(2022·吉林长春二中月考)铺设铁轨时,每两根钢轨接缝处都必须留有一定的间隙,匀速运行的列车经过轨端接缝处时,车轮就会受到一次冲击。由于每一根钢轨长度相等,所以这个冲击力是周期性的,列车受到周期性的冲击做受迫振动。普通钢轨长为12.6 m,列车的固有周期为0.315 s。下列说法正确的是
A.列车的危险速率为40 m/s
B.列车过桥需要减速,是为了防止列车发生共振现象
C.列车运行的振动频率和列车的固有频率总是相等的
D.增加钢轨的长度有利于列车高速运行
√
√
生活中的振动
一
阻尼振动
二
受迫振动与共振
三
共振的应用防止
自由振动
阻尼振动
仅在回复力作用下的振动
定义
产生原因
图像
振幅不断减小
克服阻力做功,机械能减少。
周期(频率)不变
受迫振动
共振
驱动力
受迫振动
周期(频率)
周期性外力
在驱动力作用下的振动
总等于驱动力的周期(频率)
定义
条件
共振曲线
受迫振动的振幅最大
共振的应用
共振的防止
使f驱=f固或使f驱接近f固
使f驱远离f固
f驱=f固
同课章节目录
- 第1章 动量及其守恒定律
- 第1节 动量和动量定理
- 第2节 动量守恒定律及其应用
- 第3节 科学验证:动量守恒定律
- 第4节 弹性碰撞与非弹性碰撞
- 第2章 机械振动
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 科学测量:用单摆测量重力加速度
- 第5节 生活中的振动
- 第3章 机械波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第4章 光的折射和全反射
- 第1节 光的折射
- 第2节 科学测量:玻璃的折射率
- 第3节 光的全反射
- 第4节 光导纤维及其应用
- 第5章 光的干涉、衍射和偏振
- 第1节 光的干涉
- 第2节 科学测量:用双缝干涉测光的波长
- 第3节 光的衍射
- 第4节 光的偏振
- 第5节 激光与全息照相
