第二十二章 二次函数复习课件
文档属性
| 名称 | 第二十二章 二次函数复习课件 |  | |
| 格式 | zip | ||
| 文件大小 | 429.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-28 08:09:59 | ||
图片预览






文档简介
课件20张PPT。二次函数复习课华震东出品1、二次函数的定义
定义: y=ax2 + bx + c ( a 、 b 、 c 是常数, a ≠ 0 )
定义要点:①a ≠ 0 ②最高次数为2
③代数式一定是整式
练习:1、y=-x2,y=2x2-2/x,y=100-5 x2,
y=3 x2-2x3+5,其中是二次函数的有____个。 2.当m_______时,函数y=(m+1)χ - 2χ+1
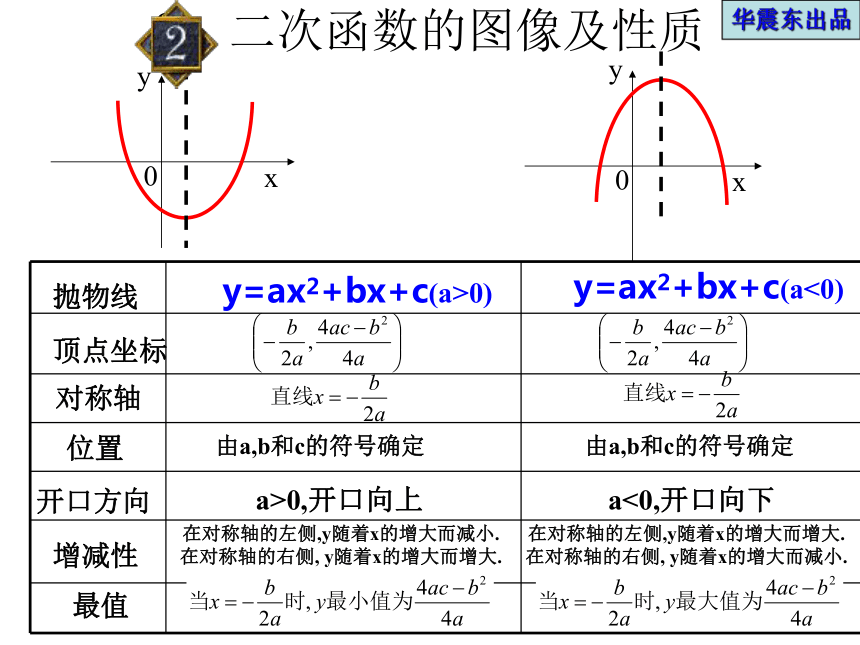
是二次函数?华震东出品2、二次函数的图像及性质 抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)由a,b和c的符号确定由a,b和c的符号确定a>0,开口向上a<0,开口向下在对称轴的左侧,y随着x的增大而减小.
在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 华震东出品例2:
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,A,B的坐标。
(3)x为何值时,y随的增大而减少,x为何值时,y有最大(小)值,这个最大(小)值是多少?
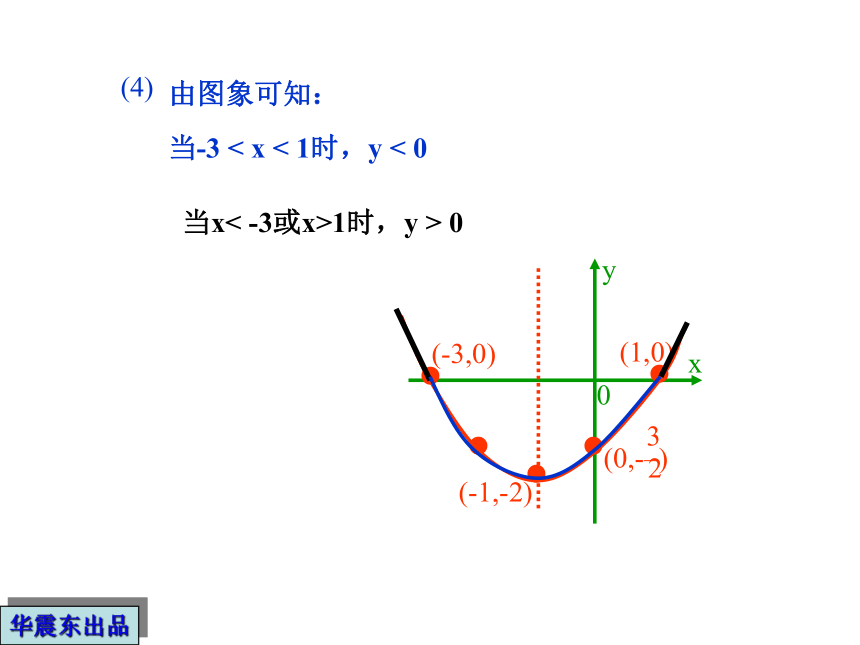
(4)x为何值时,y<0?x为何值时,y>0?
已知二次函数华震东出品
0?(-1,-2)??(0,-–)??(-3,0)(1,0)3 2yx由图象可知: 当x< -3或x>1时,y > 0当-3 < x < 1时,y < 0(4)华震东出品2,顶点式:已知抛物线顶点坐标(h, k),通常设抛物线解析式为_______________
求出表达式后化为一般形式.3,交点式:已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为_____________
求出表达式后化为一般形式.1、一般式:已知抛物线上的三点,通常设解析式为________________ y=ax2+bx+c(a≠0) y=a(x-h)2+k(a≠0)y=a(x-x1)(x-x2) (a≠0)3、求抛物线解析式的三种方法华震东出品练习:根据下列条件,求二次函数的解析式。(1)、图象经过(0,0), (1,-2) , (2,3) 三点;(2)、图象的顶点(2,3), 且经过点(3,1) ;(3)、图象经过(0,0), (12,0) ,且最高点 的纵坐标是3 。华震东出品 例1、已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。求a、b、c。解:∵二次函数的最大值是2
∴抛物线的顶点纵坐标为2
又∵抛物线的顶点在直线y=x+1上
∴当y=2时,x=1
∴顶点坐标为( 1 , 2)
∴设二次函数的解析式为y=a(x-1)2+2
又∵图象经过点(3,-6)
∴-6=a (3-1)2+2 ∴a=-2
∴二次函数的解析式为y=-2(x-1)2+2
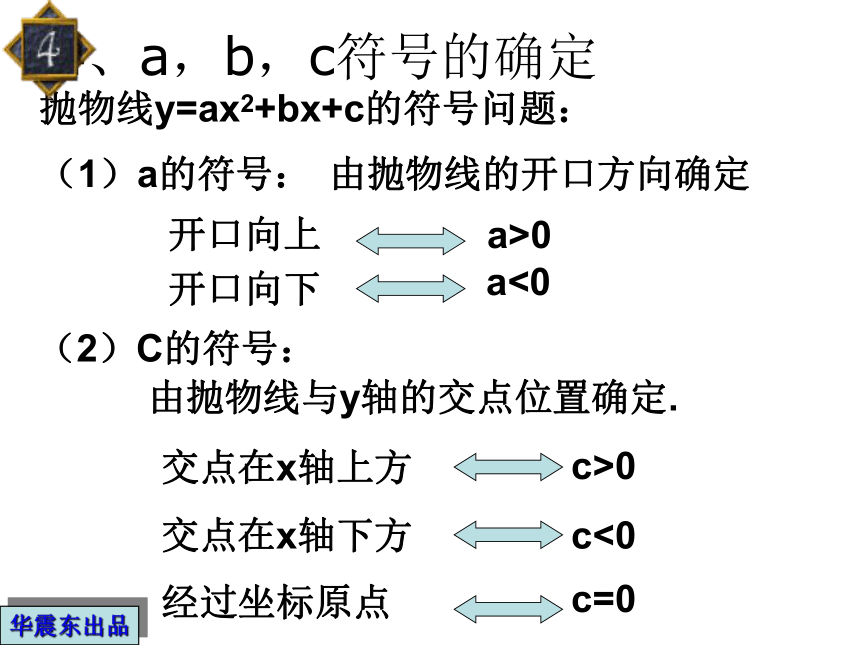
即: y=-2x2+4x华震东出品4、a,b,c符号的确定抛物线y=ax2+bx+c的符号问题:(1)a的符号:由抛物线的开口方向确定开口向上a>0开口向下a<0(2)C的符号:由抛物线与y轴的交点位置确定.交点在x轴上方c>0交点在x轴下方c<0经过坐标原点c=0华震东出品(3)b的符号:由对称轴的位置确定对称轴在y轴左侧a、b同号对称轴在y轴右侧a、b异号对称轴是y轴b=0(4)b2-4ac的符号:由抛物线与x轴的交点个数确定与x轴有两个交点b2-4ac>0与x轴有一个交点b2-4ac=0与x轴无交点b2-4ac<0华震东出品1、二次函数y=ax2+bx+c(a≠0)的图象如图
所示,则a、b、c的符号为( )
A、a<0,b>0,c>0 B、a<0,b>0,c<0
C、a<0,b<0,c>0 D、a<0,b<0,c<0 2、二次函数y=ax2+bx+c(a≠0)的图象
如图所示,则a、b、c的符号为( )
A、a>0,b>0,c=0 B、a<0,b>0,c=0
C、a<0,b<0,c<0 D、a>0,b<0,c=0 3、二次函数y=ax2+bx+c(a≠0)的图象如图
所示,则a、b、c 、 △的符号为( )
A、a>0,b=0,c>0,△>0 B、a<0,b>0,c<0,△=0
C、a>0,b=0,c<0,△>0 D、a<0,b=0,c<0,△<0 BACooo练习:熟练掌握a,b, c,△与抛物线图象的关系(上正、下负)(左同、右异) ·c华震东出品4.抛物线y=ax2+bx+c(a≠0)的图象经过原点和
二、三、四象限,判断a、b、c的符号情况:
a 0,b 0,c 0.
<=<5.抛物线y=ax2+bx+c(a≠0)的图象经过原点,
且它的顶点在第三象限,则a、b、c满足
的条件是:a 0,b 0,c 0. >=6.二次函数y=ax2+bx+c中,如果a>0,b<0,c<0,
那么这个二次函数图象的顶点必在第 象限 先根据题目的要求画出函数的草图,再根据
图象以及性质确定结果(数形结合的思想)四>华震东出品5、抛物线的平移左加右减,上加下减练习
⑴二次函数y=2x2的图象向 平移 个单位可得到y=2x2-3的图象;
二次函数y=2x2的图象向 平移 个单位可得到y=2(x-3)2的图象。
⑵二次函数y=2x2的图象先向 平移 个单位,再向 平移 个单位可得到函数y=2(x+1)2+2的图象。下3右3左1上2华震东出品
练习:
(3)由二次函数y=x2的图象经过如何平移可以得到函数y=x2-5x+6的图象.
y=x2-5x+6 华震东出品6二次函数与一元二次方程的关系一元二次方程根的情况与b2-4ac的关系
我们知道:代数式b2-4ac对于方程的根起着关键的作用.
华震东出品二次函数y=ax2+bx+c的图象和x轴交点的横坐标,便是对应的一元二次方程ax2+bx+c=0的解。
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
(1)有两个交点
(2)有一个交点
(3)没有交点二次函数与一元二次方程b2 – 4ac > 0b2 – 4ac= 0b2 – 4ac< 0若抛物线y=ax2+bx+c与x轴有交点,则b2 – 4ac≥0华震东出品与x轴有两个不
同的交点
(x1,0)
(x2,0)有两个不同的解x=x1,x=x2b2-4ac>0与x轴有唯一个
交点有两个相等的解
x1=x2=b2-4ac=0与x轴没有
交点没有实数根b2-4ac<0华震东出品例(1)如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m=_,此时抛物线 y=x2-2x+m与x轴有 个交点.(2)已知抛物线 y=x2–8x+c的顶点在 x轴上,则c=__.1116 (3)一元二次方程 3x2+x-10=0的两个根是x1= -2 ,x2=5/3, 那么二次函数y= 3x2+x-10与x轴的交点坐标是__.
(-2、0)(5/3、0)华震东出品1.已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的
形状相同,顶点在直线x=1上,且顶点到x轴的距离
为5,请写出满足此条件的抛物线的解析式.解:?抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同
? a=1或-1
又?顶点在直线x=1上,且顶点到x轴的距离为5,
? 顶点为(1,5)或(1,-5)
所以其解析式为:
(1) y=(x-1)2+5 (2) y=(x-1)2-5
(3) y=-(x-1)2+5 (4) y=-(x-1)2-5
7二次函数的综合运用 华震东出品华震东出品
定义: y=ax2 + bx + c ( a 、 b 、 c 是常数, a ≠ 0 )
定义要点:①a ≠ 0 ②最高次数为2
③代数式一定是整式
练习:1、y=-x2,y=2x2-2/x,y=100-5 x2,
y=3 x2-2x3+5,其中是二次函数的有____个。 2.当m_______时,函数y=(m+1)χ - 2χ+1
是二次函数?华震东出品2、二次函数的图像及性质 抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)由a,b和c的符号确定由a,b和c的符号确定a>0,开口向上a<0,开口向下在对称轴的左侧,y随着x的增大而减小.
在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 华震东出品例2:
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,A,B的坐标。
(3)x为何值时,y随的增大而减少,x为何值时,y有最大(小)值,这个最大(小)值是多少?
(4)x为何值时,y<0?x为何值时,y>0?
已知二次函数华震东出品
0?(-1,-2)??(0,-–)??(-3,0)(1,0)3 2yx由图象可知: 当x< -3或x>1时,y > 0当-3 < x < 1时,y < 0(4)华震东出品2,顶点式:已知抛物线顶点坐标(h, k),通常设抛物线解析式为_______________
求出表达式后化为一般形式.3,交点式:已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为_____________
求出表达式后化为一般形式.1、一般式:已知抛物线上的三点,通常设解析式为________________ y=ax2+bx+c(a≠0) y=a(x-h)2+k(a≠0)y=a(x-x1)(x-x2) (a≠0)3、求抛物线解析式的三种方法华震东出品练习:根据下列条件,求二次函数的解析式。(1)、图象经过(0,0), (1,-2) , (2,3) 三点;(2)、图象的顶点(2,3), 且经过点(3,1) ;(3)、图象经过(0,0), (12,0) ,且最高点 的纵坐标是3 。华震东出品 例1、已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。求a、b、c。解:∵二次函数的最大值是2
∴抛物线的顶点纵坐标为2
又∵抛物线的顶点在直线y=x+1上
∴当y=2时,x=1
∴顶点坐标为( 1 , 2)
∴设二次函数的解析式为y=a(x-1)2+2
又∵图象经过点(3,-6)
∴-6=a (3-1)2+2 ∴a=-2
∴二次函数的解析式为y=-2(x-1)2+2
即: y=-2x2+4x华震东出品4、a,b,c符号的确定抛物线y=ax2+bx+c的符号问题:(1)a的符号:由抛物线的开口方向确定开口向上a>0开口向下a<0(2)C的符号:由抛物线与y轴的交点位置确定.交点在x轴上方c>0交点在x轴下方c<0经过坐标原点c=0华震东出品(3)b的符号:由对称轴的位置确定对称轴在y轴左侧a、b同号对称轴在y轴右侧a、b异号对称轴是y轴b=0(4)b2-4ac的符号:由抛物线与x轴的交点个数确定与x轴有两个交点b2-4ac>0与x轴有一个交点b2-4ac=0与x轴无交点b2-4ac<0华震东出品1、二次函数y=ax2+bx+c(a≠0)的图象如图
所示,则a、b、c的符号为( )
A、a<0,b>0,c>0 B、a<0,b>0,c<0
C、a<0,b<0,c>0 D、a<0,b<0,c<0 2、二次函数y=ax2+bx+c(a≠0)的图象
如图所示,则a、b、c的符号为( )
A、a>0,b>0,c=0 B、a<0,b>0,c=0
C、a<0,b<0,c<0 D、a>0,b<0,c=0 3、二次函数y=ax2+bx+c(a≠0)的图象如图
所示,则a、b、c 、 △的符号为( )
A、a>0,b=0,c>0,△>0 B、a<0,b>0,c<0,△=0
C、a>0,b=0,c<0,△>0 D、a<0,b=0,c<0,△<0 BACooo练习:熟练掌握a,b, c,△与抛物线图象的关系(上正、下负)(左同、右异) ·c华震东出品4.抛物线y=ax2+bx+c(a≠0)的图象经过原点和
二、三、四象限,判断a、b、c的符号情况:
a 0,b 0,c 0.
<=<5.抛物线y=ax2+bx+c(a≠0)的图象经过原点,
且它的顶点在第三象限,则a、b、c满足
的条件是:a 0,b 0,c 0. >=6.二次函数y=ax2+bx+c中,如果a>0,b<0,c<0,
那么这个二次函数图象的顶点必在第 象限 先根据题目的要求画出函数的草图,再根据
图象以及性质确定结果(数形结合的思想)四>华震东出品5、抛物线的平移左加右减,上加下减练习
⑴二次函数y=2x2的图象向 平移 个单位可得到y=2x2-3的图象;
二次函数y=2x2的图象向 平移 个单位可得到y=2(x-3)2的图象。
⑵二次函数y=2x2的图象先向 平移 个单位,再向 平移 个单位可得到函数y=2(x+1)2+2的图象。下3右3左1上2华震东出品
练习:
(3)由二次函数y=x2的图象经过如何平移可以得到函数y=x2-5x+6的图象.
y=x2-5x+6 华震东出品6二次函数与一元二次方程的关系一元二次方程根的情况与b2-4ac的关系
我们知道:代数式b2-4ac对于方程的根起着关键的作用.
华震东出品二次函数y=ax2+bx+c的图象和x轴交点的横坐标,便是对应的一元二次方程ax2+bx+c=0的解。
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
(1)有两个交点
(2)有一个交点
(3)没有交点二次函数与一元二次方程b2 – 4ac > 0b2 – 4ac= 0b2 – 4ac< 0若抛物线y=ax2+bx+c与x轴有交点,则b2 – 4ac≥0华震东出品与x轴有两个不
同的交点
(x1,0)
(x2,0)有两个不同的解x=x1,x=x2b2-4ac>0与x轴有唯一个
交点有两个相等的解
x1=x2=b2-4ac=0与x轴没有
交点没有实数根b2-4ac<0华震东出品例(1)如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m=_,此时抛物线 y=x2-2x+m与x轴有 个交点.(2)已知抛物线 y=x2–8x+c的顶点在 x轴上,则c=__.1116 (3)一元二次方程 3x2+x-10=0的两个根是x1= -2 ,x2=5/3, 那么二次函数y= 3x2+x-10与x轴的交点坐标是__.
(-2、0)(5/3、0)华震东出品1.已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的
形状相同,顶点在直线x=1上,且顶点到x轴的距离
为5,请写出满足此条件的抛物线的解析式.解:?抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同
? a=1或-1
又?顶点在直线x=1上,且顶点到x轴的距离为5,
? 顶点为(1,5)或(1,-5)
所以其解析式为:
(1) y=(x-1)2+5 (2) y=(x-1)2-5
(3) y=-(x-1)2+5 (4) y=-(x-1)2-5
7二次函数的综合运用 华震东出品华震东出品
同课章节目录
