专题1.9截一个几何体 直通中考(含解析)2023-2024学年七年级数学上册北师大版专项讲练
文档属性
| 名称 | 专题1.9截一个几何体 直通中考(含解析)2023-2024学年七年级数学上册北师大版专项讲练 |

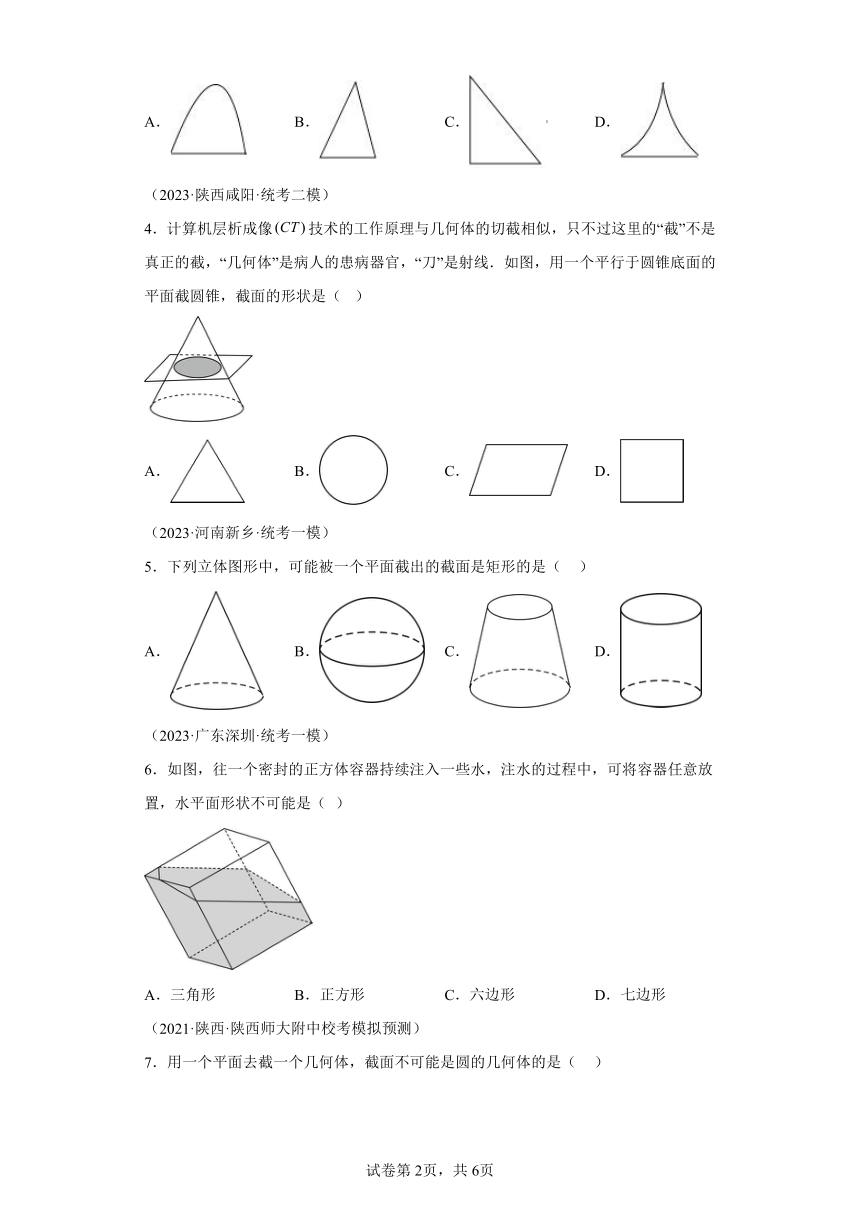
|
|
| 格式 | docx | ||
| 文件大小 | 292.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览


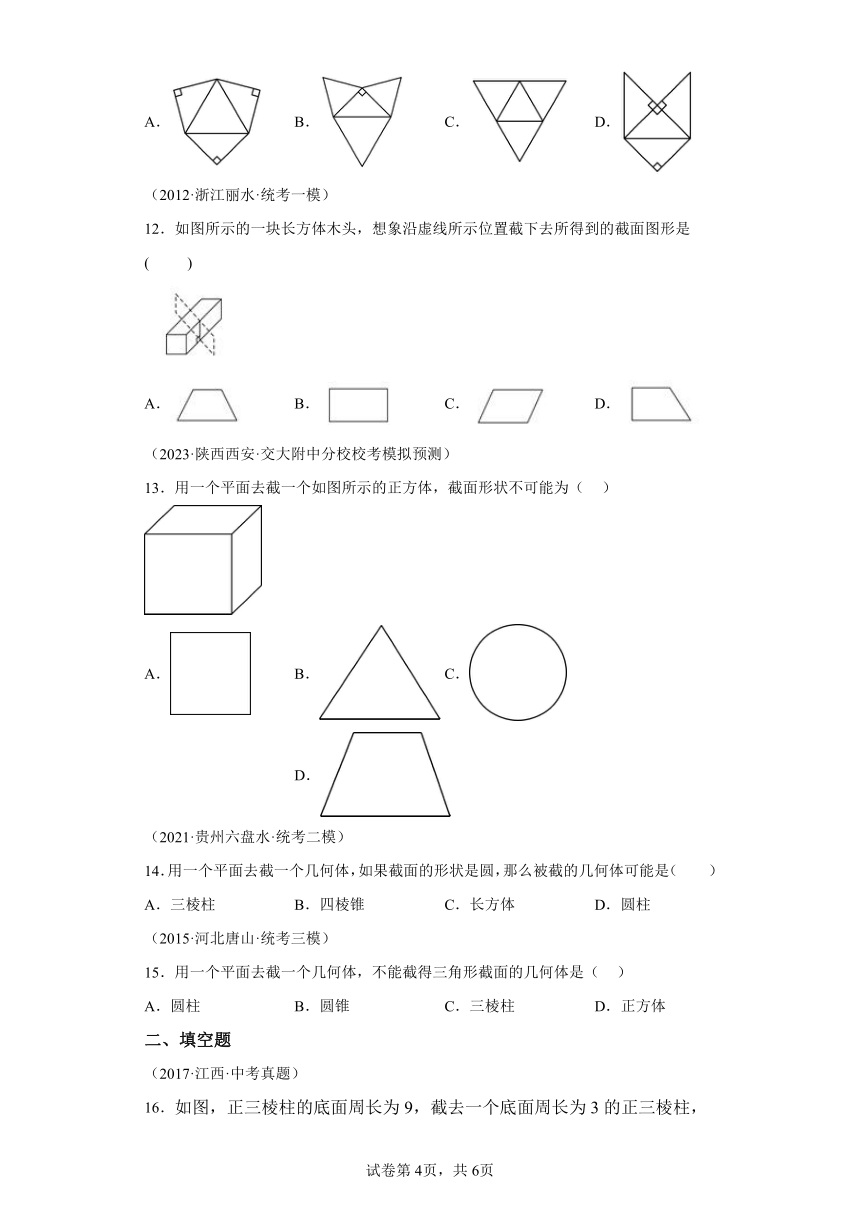

文档简介
专题1.9 截一个几何体(直通中考)
【要点回顾】
1.常见几何体的截面;根据截面判断几何体;
2.决定截面形状的因素:(1)原几何体的形状;(2)截面方向和角度.
3.对于同一个几何体,截面方向不同,所得的截面形状一般也不同,同一几何体可能有多种不同的形状截面.
一、单选题
(2022·贵州贵阳·统考中考真题)
1.如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是( )
A. B. C. D.
(2018·江苏南京·统考中考真题)
2.用一个平面去截正方体(如图),下列关于截面(截出的面)的形状的结论:①可能是锐角三角形;②可能是直角三角形;③可能是钝角三角形;④可能是平行四边形.其中所有正确结论的序号是( )
A.①② B.①④ C.①②④ D.①②③④
(2017·江苏扬州·中考真题)
3.经过圆锥顶点的截面的形状可能是( )
A. B. C. D.
(2023·陕西咸阳·统考二模)
4.计算机层析成像技术的工作原理与几何体的切截相似,只不过这里的“截”不是真正的截,“几何体”是病人的患病器官,“刀”是射线.如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是( )
A. B. C. D.
(2023·河南新乡·统考一模)
5.下列立体图形中,可能被一个平面截出的截面是矩形的是( )
A. B. C. D.
(2023·广东深圳·统考一模)
6.如图,往一个密封的正方体容器持续注入一些水,注水的过程中,可将容器任意放置,水平面形状不可能是( )
A.三角形 B.正方形 C.六边形 D.七边形
(2021·陕西·陕西师大附中校考模拟预测)
7.用一个平面去截一个几何体,截面不可能是圆的几何体的是( )
A. B. C. D.
8.(2022·陕西西安·校考三模)正方体的截面形状不可能是( )
A.三角形 B.五边形 C.六边形 D.七边形
(2019·河北·模拟预测)
9.如图,在一密闭的圆柱形玻璃杯中装一半的水,水平放置时,水面的形状是( )
A.圆 B.平行四边形 C.椭圆 D.长方形
(2019·福建三明·校联考一模)
10.用一个平面去截下列四个几何体,可以得到三角形截面的几何体有( )
A.1个 B.2个 C.3个 D.4个
(2022·广东揭阳·统考一模)
11.如图,在正方体中,沿对角线BD和顶点A所在的平面截出几何体A﹣BCD,则这个几何体的展开图可能是( )
A. B. C. D.
(2012·浙江丽水·统考一模)
12.如图所示的一块长方体木头,想象沿虚线所示位置截下去所得到的截面图形是( )
A. B. C. D.
(2023·陕西西安·交大附中分校校考模拟预测)
13.用一个平面去截一个如图所示的正方体,截面形状不可能为( )
A. B. C. D.
(2021·贵州六盘水·统考二模)
14.用一个平面去截一个几何体,如果截面的形状是圆,那么被截的几何体可能是( )
A.三棱柱 B.四棱锥 C.长方体 D.圆柱
(2015·河北唐山·统考三模)
15.用一个平面去截一个几何体,不能截得三角形截面的几何体是( )
A.圆柱 B.圆锥 C.三棱柱 D.正方体
二、填空题
(2017·江西·中考真题)
16.如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是 .
(2015·黑龙江大庆·统考中考真题)
17.用一个平面去截一个几何体,截面形状为三角形,则这个几何体可能为:①正方体;②圆柱;③圆锥;④正三棱柱 (写出所有正确结果的序号).
(2004·浙江温州·中考真题)
18.把一个边长为2 cm的立方体截成八个边长为1 cm的小立方体,至少需要截 次.
(2020·广东·统考一模)
19.在正方体的截面中,最多可以截出 边形.
(2019·浙江台州·统考二模)
20.把一个长方体切去一个角后,剩下的几何体的顶点个数为 .
(2019·浙江台州·统考二模)
21.如图,一个5×5×5的正方体,先在它的前后方向正中央开凿一个“十字形”的孔(打通),再在它的上下方向正中央也开凿一个“十字形”的孔(打通),最后在它的左右方向正中央开凿一个“十字形”的孔(打通),这样得到一个被凿空了的几何体,则所得几何体的体积为 .
(2019·山东青岛·校考三模)
22.如图是棱长为2cm的正方体,过相邻三条棱的中点截取一个小正方体,则剩下部分的表面积为 cm2.
(2018·山东滨州·统考一模)
23.如图,正三棱柱的底面周长为15,截去一个底面周长为6的正三棱柱,所得几何体的俯视图的周长是 ,面积是 .
(2022·江苏南京·统考一模)
24.若用平面分别截下列几何体:①三棱柱;②三棱锥;③正方体;④圆锥;⑤球,截面可能是三角形的是 .(填序号)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据圆锥体的立体图形判断即可.
【详解】用平行底面的平面截圆锥体,截面是圆形,
故选:B.
【点睛】本题考查了截面图形的判断,具有一定的空间想象力是解答本题的关键.
2.B
【分析】利用正方体和正四面体的性质,分析4个选项,即可得出结论.
【详解】解::①正方体的截面是三角形时,为锐角三角形,正确;
②③正四面体的截面不可能是直角三角形或钝角三角形,不正确;
④若正四面体的截面是可以是平行四边形,正确.
故选B.
【点睛】此题主要考查了正方体的截面,考查学生分析解决问题的能力,属于中档题.
3.B
【详解】试题解析:经过圆锥顶点的截面的形状可能B中图形,
故选B.
4.B
【分析】根据用一个平行于圆锥底面的平面截圆锥,截面的形状是圆即可得出答案.
【详解】解:用一个平行于圆锥底面的平面截圆锥,截面的形状是圆,
故选:B.
【点睛】本题考查了截一个几何体,掌握用一个平行于圆锥底面的平面截圆锥,截面的形状是圆是解题的关键.
5.D
【分析】根据几何体截面的概念求解即可.
【详解】解:由题意可得,可能被一个平面截出的截面是矩形的是圆柱体,
故选:D.
【点睛】本题考查的是几何体截面的形状,截面的形状既与被截几何体有关,还与截面的角度和方向有关.认真观察图中的截面是解题的关键.
6.D
【分析】正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,因此截面的形状可能是:三角形、四边形、五边形、六边形,即可得到答案;
【详解】解:∵正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,
∴截面的形状可能是:三角形、四边形、五边形、六边形,
故选D.
【点睛】本题考查了正方体的截面,解题的关键是熟练掌握面面相交等到线.
7.C
【分析】根据一个几何体有几个面,则截面最多为几边形,由于棱柱没有曲边,所以用一个平面去截棱柱,截面不可能是圆.
【详解】解:用一个平面去截圆锥或圆柱,截面可能是圆,
用一个平面去截球,截面是圆,
但用一个平面去截棱柱,截面不可能是圆.
故选:C.
【点睛】本题考查了截一个几何体:用一个平面去截一个几何体,截出的面叫做截面.截面的形状随截法的不同而改变,一般为多边形或圆,也可能是不规则图形,一般的截面与几何体的几个面相交就得到几条交线,截面就是几边形,因此,若一个几何体有几个面,则截面最多为几边形.
8.D
【分析】正方体有六个面,截面与其六个面相交最多得六边形,不可能是七边形或多于七边的图形.
【详解】解:用平面去截正方体,得的截面可能为三角形、四边形、五边形、六边形,不可能为七边形.
故选:D.
【点睛】本题考查正方体的截面.熟记正方体截面的四种情况是解题的关键.
9.D
【分析】根据圆柱的横截面即可得出答案.
【详解】解:根据图形可得,水面的形状为:长方形,
故选:D.
【点睛】本题考查了认识立体图形,关键是要知道垂直于圆柱底面的截面是长方形,平行圆柱底面的截面是圆形.
10.B
【分析】根据各个几何体截面的形状逐个判断即可.
【详解】解:用一个平面去截圆锥、三棱柱可以得到三角形截面,
故选:B.
【点睛】本题考查认识立体图形和截几何体,掌握立体图形的特征和截面的形状是正确判断的关键.
11.A
【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.
【详解】解:观察图形可知,如图,在正方体中,沿对角线BD和顶点A所在的平面截出几何体A-BCD,则这个几何体的展开图可能是.
故选:A.
【点睛】本题考查了截一个几何体和几何体的展开图.解决此类问题,要充分考虑各个面的特点及位置.
12.B
【分析】首先根据两组对边平行,可确定为平行四边形;又有一角为直角,故截面图形是矩形.
【详解】解:长方体的截面,经过长方体四个侧面,长方体中,对边平行,故可确定为平行四边形,交点垂直于底边,故为矩形.
故选B.
【点睛】截面的形状既与被截的几何体有关,还与截面的角度和方向有关.对于这类题,最好是动手动脑相结合,亲自动手做一做,从中学会分析和归纳的思想方法.
13.C
【分析】正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,截面也不可能有弧度,因此截面形状不可能为圆.
【详解】解:用一个平面无论如何去截,截面也不可能有弧度,因此截面形状不可能为圆.
故选:C.
【点睛】本题考查正方体的截面.正方体有六个面,截面与其六个面相交最多得六边形,不可能是七边形或多于七边的图形或其它的弧形.
14.D
【分析】根据每一个几何体的截面形状判断即可.
【详解】解:用一个平面去截一个几何体,三棱柱,四棱锥,长方体的截面形状不可能是圆,只可能是多边形,
圆柱的截面形状可能是圆,
故选:D.
【点睛】本题考查了截一个几何体,熟练掌握每一个几何体的截面形状是解题的关键.
15.A
【分析】根据正方体、球体、棱柱、圆柱的形状特点判断即可.
【详解】A、圆柱的截面跟圆、四边形有关,截面不可能是三角形,符合题意;
B、过圆锥的顶点和下底圆心的面得到的截面是三角形,不符合题意;
C、过三棱柱的三个面得到的截面是三角形,不符合题意;
D、过正方体的三个面得到的截面是三角形,不符合题意.
故选A.
【点睛】本题主要考查了截面的形状,截面的形状既与被截的几何体有关,还与截面的角度和方向有关.对于这类题,最好是动手动脑相结合,从中学会分析和归纳的思想方法.
16.8
【详解】试题分析:根据从上边看得到的图形是俯视图,可知从上边看是一个梯形:上底是1,下底是3,两腰是2,
周长是1+2+2+3=8,
故答案为8.
考点:1、简单组合体的三视图;2、截一个几何体
17.①③④
【分析】当截面的角度和方向不同时,圆柱体的截面无论什么方向截取圆柱都不会截得三角形.
【详解】解:①正方体能截出三角形;
②圆柱不能截出三角形;
③圆锥沿着母线截几何体可以截出三角形;
④正三棱柱能截出三角形.
故截面可能是三角形的有3个.
故答案为:①③④.
【点睛】本题考查几何体的截面,截面的形状既与被截的几何体有关,还与截面的角度和方向有关.
18.3
【分析】要截成八个边长为1cm的小立方体,应该横着从中间截一次,然后竖着从中间截两次,并且这两次截得方向垂直.
【详解】解:如图
要截成八个边长为1cm的小立方体,应该横着从中间截一次,然后竖着从中间截两次,并且这两次截得方向垂直.
∴至少需要截3次
故答案为:3.
【点睛】本题考查了认识立体图形.解题的关键在于掌握立体图形截面的定义及所截的几何体的形状.
19.六
【分析】根据平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形即可得出答案.
【详解】用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,
因此最多可以截出六边形,
故答案为:六.
【点睛】本题考查了截几何体,正确运用空间想象能力是解题关键.
20.7,8,9,10.
【分析】结合长方体,动手操作,得出结果即可.
【详解】把一个长方体切去一个角后,剩下的几何体的顶点个数为7,8,9,10,
故答案为:7,8,9,10
【点睛】本题考查截一个几何体,解题的关键是知道截面的形状既与被截的几何体有关,还与截面的角度和方向有关.
21.76
【分析】从5×5×5的正方体的8个顶点进行分割,可得8个2×2×2的正方体,再加上12条棱中间的12个小正方体,依此求得小正方体的个数,再乘以1个小正方体的体积即可求解.
【详解】如图所示:该正方体可按如图方式分割,
则体积为(1×1×1)×(8×8+12)
=1×76
=76,
故所得几何体的体积为76.
故答案为:76.
【点睛】本题考查了截一个几何体,正方体的体积,关键是得到小正方体的个数.
22.24
【详解】由于是在正方体的顶点上截取一个小正方体,去掉小正方形的三个面的面积,同时又多出小正方形的三个面的面积,表面积没变,可得:
过相邻三条棱的中点截取一个小正方体,则剩下部分的表面积为2×2×6=24cm2.
故答案是:24.
23. 13
【详解】∵此几何体的俯视图是等腰梯形,
且上底是,下底是,
∴腰长为5-2=3,
∴这个等腰梯形的周长为:2+5+3+3=13;
∵这个等腰梯形的高是:,
∴这个等腰梯形的面积为:.
故答案为13,.
24.①②③④
【分析】当截面的角度和方向不同时,球的截面无论什么方向截取圆柱都不会截得三角形.
【详解】解:①用平面截三棱柱时,可以得到三角形截面.
②当平面平行于三棱锥的任意面时,得到的截面都是三角形.
③当平面经过正方体的三个顶点时,所得到的截面为三角形.
④当平面沿着母线截圆锥时,可以得到三角形截面.
⑤用平面球时,无论什么方向截取圆柱都不会截得三角形.
故答案为∶①②③④.
【点睛】本题主要考查的是截面的相关知识,解题的关键是明确截面的形状既与被截的几何体有关系,又与截面的角度和方向有关.
答案第1页,共2页
答案第1页,共2页
【要点回顾】
1.常见几何体的截面;根据截面判断几何体;
2.决定截面形状的因素:(1)原几何体的形状;(2)截面方向和角度.
3.对于同一个几何体,截面方向不同,所得的截面形状一般也不同,同一几何体可能有多种不同的形状截面.
一、单选题
(2022·贵州贵阳·统考中考真题)
1.如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是( )
A. B. C. D.
(2018·江苏南京·统考中考真题)
2.用一个平面去截正方体(如图),下列关于截面(截出的面)的形状的结论:①可能是锐角三角形;②可能是直角三角形;③可能是钝角三角形;④可能是平行四边形.其中所有正确结论的序号是( )
A.①② B.①④ C.①②④ D.①②③④
(2017·江苏扬州·中考真题)
3.经过圆锥顶点的截面的形状可能是( )
A. B. C. D.
(2023·陕西咸阳·统考二模)
4.计算机层析成像技术的工作原理与几何体的切截相似,只不过这里的“截”不是真正的截,“几何体”是病人的患病器官,“刀”是射线.如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是( )
A. B. C. D.
(2023·河南新乡·统考一模)
5.下列立体图形中,可能被一个平面截出的截面是矩形的是( )
A. B. C. D.
(2023·广东深圳·统考一模)
6.如图,往一个密封的正方体容器持续注入一些水,注水的过程中,可将容器任意放置,水平面形状不可能是( )
A.三角形 B.正方形 C.六边形 D.七边形
(2021·陕西·陕西师大附中校考模拟预测)
7.用一个平面去截一个几何体,截面不可能是圆的几何体的是( )
A. B. C. D.
8.(2022·陕西西安·校考三模)正方体的截面形状不可能是( )
A.三角形 B.五边形 C.六边形 D.七边形
(2019·河北·模拟预测)
9.如图,在一密闭的圆柱形玻璃杯中装一半的水,水平放置时,水面的形状是( )
A.圆 B.平行四边形 C.椭圆 D.长方形
(2019·福建三明·校联考一模)
10.用一个平面去截下列四个几何体,可以得到三角形截面的几何体有( )
A.1个 B.2个 C.3个 D.4个
(2022·广东揭阳·统考一模)
11.如图,在正方体中,沿对角线BD和顶点A所在的平面截出几何体A﹣BCD,则这个几何体的展开图可能是( )
A. B. C. D.
(2012·浙江丽水·统考一模)
12.如图所示的一块长方体木头,想象沿虚线所示位置截下去所得到的截面图形是( )
A. B. C. D.
(2023·陕西西安·交大附中分校校考模拟预测)
13.用一个平面去截一个如图所示的正方体,截面形状不可能为( )
A. B. C. D.
(2021·贵州六盘水·统考二模)
14.用一个平面去截一个几何体,如果截面的形状是圆,那么被截的几何体可能是( )
A.三棱柱 B.四棱锥 C.长方体 D.圆柱
(2015·河北唐山·统考三模)
15.用一个平面去截一个几何体,不能截得三角形截面的几何体是( )
A.圆柱 B.圆锥 C.三棱柱 D.正方体
二、填空题
(2017·江西·中考真题)
16.如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是 .
(2015·黑龙江大庆·统考中考真题)
17.用一个平面去截一个几何体,截面形状为三角形,则这个几何体可能为:①正方体;②圆柱;③圆锥;④正三棱柱 (写出所有正确结果的序号).
(2004·浙江温州·中考真题)
18.把一个边长为2 cm的立方体截成八个边长为1 cm的小立方体,至少需要截 次.
(2020·广东·统考一模)
19.在正方体的截面中,最多可以截出 边形.
(2019·浙江台州·统考二模)
20.把一个长方体切去一个角后,剩下的几何体的顶点个数为 .
(2019·浙江台州·统考二模)
21.如图,一个5×5×5的正方体,先在它的前后方向正中央开凿一个“十字形”的孔(打通),再在它的上下方向正中央也开凿一个“十字形”的孔(打通),最后在它的左右方向正中央开凿一个“十字形”的孔(打通),这样得到一个被凿空了的几何体,则所得几何体的体积为 .
(2019·山东青岛·校考三模)
22.如图是棱长为2cm的正方体,过相邻三条棱的中点截取一个小正方体,则剩下部分的表面积为 cm2.
(2018·山东滨州·统考一模)
23.如图,正三棱柱的底面周长为15,截去一个底面周长为6的正三棱柱,所得几何体的俯视图的周长是 ,面积是 .
(2022·江苏南京·统考一模)
24.若用平面分别截下列几何体:①三棱柱;②三棱锥;③正方体;④圆锥;⑤球,截面可能是三角形的是 .(填序号)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据圆锥体的立体图形判断即可.
【详解】用平行底面的平面截圆锥体,截面是圆形,
故选:B.
【点睛】本题考查了截面图形的判断,具有一定的空间想象力是解答本题的关键.
2.B
【分析】利用正方体和正四面体的性质,分析4个选项,即可得出结论.
【详解】解::①正方体的截面是三角形时,为锐角三角形,正确;
②③正四面体的截面不可能是直角三角形或钝角三角形,不正确;
④若正四面体的截面是可以是平行四边形,正确.
故选B.
【点睛】此题主要考查了正方体的截面,考查学生分析解决问题的能力,属于中档题.
3.B
【详解】试题解析:经过圆锥顶点的截面的形状可能B中图形,
故选B.
4.B
【分析】根据用一个平行于圆锥底面的平面截圆锥,截面的形状是圆即可得出答案.
【详解】解:用一个平行于圆锥底面的平面截圆锥,截面的形状是圆,
故选:B.
【点睛】本题考查了截一个几何体,掌握用一个平行于圆锥底面的平面截圆锥,截面的形状是圆是解题的关键.
5.D
【分析】根据几何体截面的概念求解即可.
【详解】解:由题意可得,可能被一个平面截出的截面是矩形的是圆柱体,
故选:D.
【点睛】本题考查的是几何体截面的形状,截面的形状既与被截几何体有关,还与截面的角度和方向有关.认真观察图中的截面是解题的关键.
6.D
【分析】正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,因此截面的形状可能是:三角形、四边形、五边形、六边形,即可得到答案;
【详解】解:∵正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,
∴截面的形状可能是:三角形、四边形、五边形、六边形,
故选D.
【点睛】本题考查了正方体的截面,解题的关键是熟练掌握面面相交等到线.
7.C
【分析】根据一个几何体有几个面,则截面最多为几边形,由于棱柱没有曲边,所以用一个平面去截棱柱,截面不可能是圆.
【详解】解:用一个平面去截圆锥或圆柱,截面可能是圆,
用一个平面去截球,截面是圆,
但用一个平面去截棱柱,截面不可能是圆.
故选:C.
【点睛】本题考查了截一个几何体:用一个平面去截一个几何体,截出的面叫做截面.截面的形状随截法的不同而改变,一般为多边形或圆,也可能是不规则图形,一般的截面与几何体的几个面相交就得到几条交线,截面就是几边形,因此,若一个几何体有几个面,则截面最多为几边形.
8.D
【分析】正方体有六个面,截面与其六个面相交最多得六边形,不可能是七边形或多于七边的图形.
【详解】解:用平面去截正方体,得的截面可能为三角形、四边形、五边形、六边形,不可能为七边形.
故选:D.
【点睛】本题考查正方体的截面.熟记正方体截面的四种情况是解题的关键.
9.D
【分析】根据圆柱的横截面即可得出答案.
【详解】解:根据图形可得,水面的形状为:长方形,
故选:D.
【点睛】本题考查了认识立体图形,关键是要知道垂直于圆柱底面的截面是长方形,平行圆柱底面的截面是圆形.
10.B
【分析】根据各个几何体截面的形状逐个判断即可.
【详解】解:用一个平面去截圆锥、三棱柱可以得到三角形截面,
故选:B.
【点睛】本题考查认识立体图形和截几何体,掌握立体图形的特征和截面的形状是正确判断的关键.
11.A
【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.
【详解】解:观察图形可知,如图,在正方体中,沿对角线BD和顶点A所在的平面截出几何体A-BCD,则这个几何体的展开图可能是.
故选:A.
【点睛】本题考查了截一个几何体和几何体的展开图.解决此类问题,要充分考虑各个面的特点及位置.
12.B
【分析】首先根据两组对边平行,可确定为平行四边形;又有一角为直角,故截面图形是矩形.
【详解】解:长方体的截面,经过长方体四个侧面,长方体中,对边平行,故可确定为平行四边形,交点垂直于底边,故为矩形.
故选B.
【点睛】截面的形状既与被截的几何体有关,还与截面的角度和方向有关.对于这类题,最好是动手动脑相结合,亲自动手做一做,从中学会分析和归纳的思想方法.
13.C
【分析】正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,截面也不可能有弧度,因此截面形状不可能为圆.
【详解】解:用一个平面无论如何去截,截面也不可能有弧度,因此截面形状不可能为圆.
故选:C.
【点睛】本题考查正方体的截面.正方体有六个面,截面与其六个面相交最多得六边形,不可能是七边形或多于七边的图形或其它的弧形.
14.D
【分析】根据每一个几何体的截面形状判断即可.
【详解】解:用一个平面去截一个几何体,三棱柱,四棱锥,长方体的截面形状不可能是圆,只可能是多边形,
圆柱的截面形状可能是圆,
故选:D.
【点睛】本题考查了截一个几何体,熟练掌握每一个几何体的截面形状是解题的关键.
15.A
【分析】根据正方体、球体、棱柱、圆柱的形状特点判断即可.
【详解】A、圆柱的截面跟圆、四边形有关,截面不可能是三角形,符合题意;
B、过圆锥的顶点和下底圆心的面得到的截面是三角形,不符合题意;
C、过三棱柱的三个面得到的截面是三角形,不符合题意;
D、过正方体的三个面得到的截面是三角形,不符合题意.
故选A.
【点睛】本题主要考查了截面的形状,截面的形状既与被截的几何体有关,还与截面的角度和方向有关.对于这类题,最好是动手动脑相结合,从中学会分析和归纳的思想方法.
16.8
【详解】试题分析:根据从上边看得到的图形是俯视图,可知从上边看是一个梯形:上底是1,下底是3,两腰是2,
周长是1+2+2+3=8,
故答案为8.
考点:1、简单组合体的三视图;2、截一个几何体
17.①③④
【分析】当截面的角度和方向不同时,圆柱体的截面无论什么方向截取圆柱都不会截得三角形.
【详解】解:①正方体能截出三角形;
②圆柱不能截出三角形;
③圆锥沿着母线截几何体可以截出三角形;
④正三棱柱能截出三角形.
故截面可能是三角形的有3个.
故答案为:①③④.
【点睛】本题考查几何体的截面,截面的形状既与被截的几何体有关,还与截面的角度和方向有关.
18.3
【分析】要截成八个边长为1cm的小立方体,应该横着从中间截一次,然后竖着从中间截两次,并且这两次截得方向垂直.
【详解】解:如图
要截成八个边长为1cm的小立方体,应该横着从中间截一次,然后竖着从中间截两次,并且这两次截得方向垂直.
∴至少需要截3次
故答案为:3.
【点睛】本题考查了认识立体图形.解题的关键在于掌握立体图形截面的定义及所截的几何体的形状.
19.六
【分析】根据平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形即可得出答案.
【详解】用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,
因此最多可以截出六边形,
故答案为:六.
【点睛】本题考查了截几何体,正确运用空间想象能力是解题关键.
20.7,8,9,10.
【分析】结合长方体,动手操作,得出结果即可.
【详解】把一个长方体切去一个角后,剩下的几何体的顶点个数为7,8,9,10,
故答案为:7,8,9,10
【点睛】本题考查截一个几何体,解题的关键是知道截面的形状既与被截的几何体有关,还与截面的角度和方向有关.
21.76
【分析】从5×5×5的正方体的8个顶点进行分割,可得8个2×2×2的正方体,再加上12条棱中间的12个小正方体,依此求得小正方体的个数,再乘以1个小正方体的体积即可求解.
【详解】如图所示:该正方体可按如图方式分割,
则体积为(1×1×1)×(8×8+12)
=1×76
=76,
故所得几何体的体积为76.
故答案为:76.
【点睛】本题考查了截一个几何体,正方体的体积,关键是得到小正方体的个数.
22.24
【详解】由于是在正方体的顶点上截取一个小正方体,去掉小正方形的三个面的面积,同时又多出小正方形的三个面的面积,表面积没变,可得:
过相邻三条棱的中点截取一个小正方体,则剩下部分的表面积为2×2×6=24cm2.
故答案是:24.
23. 13
【详解】∵此几何体的俯视图是等腰梯形,
且上底是,下底是,
∴腰长为5-2=3,
∴这个等腰梯形的周长为:2+5+3+3=13;
∵这个等腰梯形的高是:,
∴这个等腰梯形的面积为:.
故答案为13,.
24.①②③④
【分析】当截面的角度和方向不同时,球的截面无论什么方向截取圆柱都不会截得三角形.
【详解】解:①用平面截三棱柱时,可以得到三角形截面.
②当平面平行于三棱锥的任意面时,得到的截面都是三角形.
③当平面经过正方体的三个顶点时,所得到的截面为三角形.
④当平面沿着母线截圆锥时,可以得到三角形截面.
⑤用平面球时,无论什么方向截取圆柱都不会截得三角形.
故答案为∶①②③④.
【点睛】本题主要考查的是截面的相关知识,解题的关键是明确截面的形状既与被截的几何体有关系,又与截面的角度和方向有关.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
