江苏省苏州市高新区实验初级中学2023?2024学年八年级上学期10月份月考数学试卷(无答案)
文档属性
| 名称 | 江苏省苏州市高新区实验初级中学2023?2024学年八年级上学期10月份月考数学试卷(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 286.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览

文档简介
(
2023
2024
学年新实初二年级
10
月份月考数学试卷
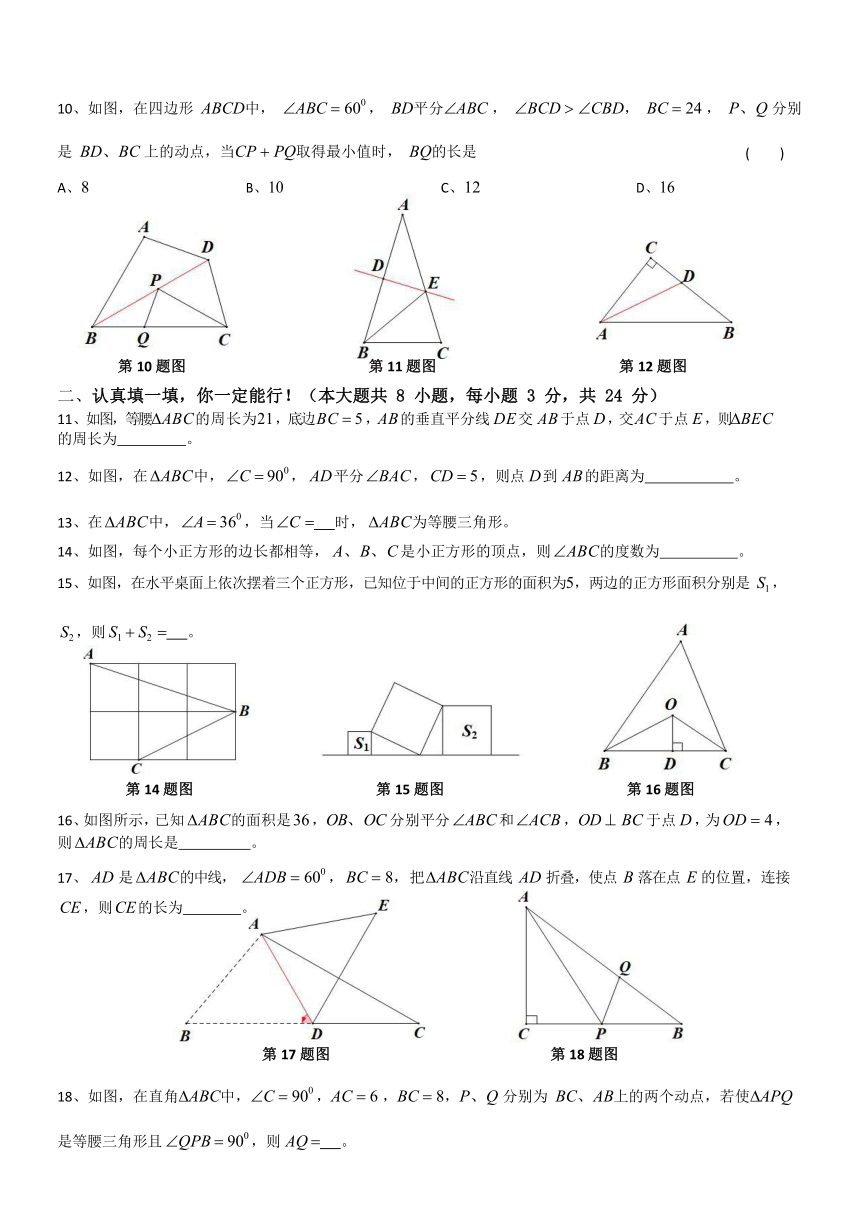
一、
细心选一选,慧眼识金!(本大题共 10 小题,每小题 2 分,共 20 分)
) (
1
、下列汽车标志中,不是轴对称图形的是
) (
(
) (
)
) (
A
、
) (
B
、
) (
C
、
) (
D
、
) (
2
、到三角形三个顶点的距离相等的点是
A
、三条角平分线的交点
C
、三边上高所在直线的交点
) (
(
) (
)
) (
B
、三边中线的交点
D
、三边的垂直平分线的交点
) (
3
、若一个直角三角形的两边长分别是
12
和
5
,则第三边长的平方是
) (
(
) (
)
) (
A
、
169
) (
B
、
169
或
119
) (
C
、
13
或
15
) (
D
、
15
) (
4
、等腰三角形的一个外角是
100
0
,则它的顶角是
) (
(
) (
)
) (
A
、
20
0
) (
B
、
80
0
) (
C
、
20
0
或
80
0
) (
D
、
40
0
或
80
0
) (
5
、把一个正方形三次对折后沿虚线剪下,如图所示,则所得的图形的是
) (
(
) (
)
) (
A
、
) (
B
、
) (
C
、
) (
D
、
) (
6
、如图,
MAN
63
0
,进行如下操作:以射线
AM
上一点
B
为圆心,以线段
BA
长为半径作弧,交射线
AN
于
) (
点
C
,连接
BC
,则
BCN
的度数是
) (
(
) (
)
) (
A
、
54
0
) (
B
、
63
0
) (
C
、
117
0
) (
D
、
126
0
) (
7
、如图,直线
a
、
b
分别经过等边
ABC
的顶点,且
a
//
b
,
1
42
0
,则
2
的度数为
) (
(
) (
)
) (
A
、
18
0
) (
B
、
42
0
) (
C
、
60
0
) (
D
、
102
0
) (
第
6
题图
8
、下列语句中,正确的是
) (
第
7
题图
) (
第
9
题图
) (
(
)
B
、等腰三角形的对称轴是底边上的高
D
、等腰三角形的对称轴就是顶角平分线
) (
A
、等腰三角形底边上的中线就是底边上的垂直平分线
C
、一条线段可看作是以它的垂直平分线为对称轴的轴对称图形
9
、如图,
AD
是
ABC
的平分线,则
AB
:
AC
等于
) (
(
) (
)
) (
A
、
BD
:
CD
) (
B
、
AD
:
CD
) (
C
、
BC
:
AD
) (
D
、
BC
:
AC
)
(
10
、如图,在四边形
ABCD
中,
ABC
60
0
,
BD
平分
ABC
,
BCD
CBD
,
BC
24
,
P
、
Q
分别
) (
是
BD
、
BC
上的动点,当
CP
PQ
取得最小值时,
BQ
的长是
) (
(
) (
)
) (
A
、
8
) (
B
、
10
) (
C
、
12
) (
D
、
16
) (
第
10
题图
) (
第
11
题图
) (
第
12
题图
) (
二、
认真填一填,你一定能行!(本大题共 8 小题,每小题 3 分,共 24 分)
1
1
、如图,等腰
AB
C
的周长为
2
1
,底边
B
C
5
,
A
B
的垂直平分线
D
E
交
A
B
于点
D
,交
A
C
于点
E
,则
BE
C
的
周
长为
。
12
、
如
图,
在
ABC
中,
C
90
0
,
AD
平
分
BAC
,
CD
5
,
则
点
D
到
AB
的
距
离为
。
) (
13
、
在
ABC
中,
A
36
0
,
当
C
时,
ABC
为
等
腰三角
形
。
14
、
如
图,每
个
小正方
形
的边长
都
相等,
A
、
B
、
C
是
小
正方形
的
顶点,
则
ABC
的
度
数为
。
15
、如图,在水平桌面上依次摆着三个正方形,已知位于中间的正方形的面积为
5
,两边的正方形面积分别是
S
1
,
) (
S
2
,则
S
1
S
2
。
) (
第
14
题图
) (
第
15
题图
) (
第
16
题图
) (
16
、
如图
所
示
,
已
知
ABC
的面
积
是
36
,
OB
、
OC
分别
平
分
ABC
和
ACB
,
OD
BC
于点
D
,
为
OD
4
,
则
ABC
的
周
长是
。
17
、
AD
是
ABC
的中线,
ADB
60
0
,
BC
8
,把
ABC
沿直线
AD
折叠,使点
B
落在点
E
的位置,连接
CE
,
则
CE
的
长
为
。
) (
第
17
题图
) (
第
18
题图
) (
18
、如图,在直角
ABC
中,
C
90
0
,
AC
6
,
BC
8
,
P
、
Q
分别为
BC
、
AB
上的两个动点,若使
APQ
) (
是
等
腰三角
形
且
QPB
90
0
,则
AQ
。
)
(
三、
耐心解一解,你一定是学习的强者!(
本大题共
9
小题,共
56
分
)
19
、(
3
分)如图,
ABC
的顶点
A
、
B
、
C
都在小正方形的顶点上,
(
1
)画
A
1
B
1
C
1
,使它与
ABC
关于直线
l
对称;
(
2
)在直线
l
找一点
P
,使点
P
到点
A
、
B
的距离之和最短。
(
3
)在直线
l
找一点
Q
,使点
Q
到
AC
、
BC
的距离线段。
) (
20
、
(
4
分)
如图所示,在
3
3
的正方形网格中,已有两个正方形被涂上颜色,请再将图中剩余的
7
个小正方形
涂黑一个,使整个图案成为一个轴对称图形。
(
请用
4
种不同的方法涂
)
) (
21
、(
4
分)已知,如图在
ABC
中,
AB
AC
,点
M
、
N
在
BC
上,且
AM
AN
,求证:
BM
CN
.
) (
22
、
(
5
分
)
如图,在
ABC
中,
ACB
90
0
,
AD
平分
BAC
,
DE
AB
于点
E
。
求证:直线
AD
是线段
CE
的垂直平分线。
) (
23
、(
6
分)如图,在四边形
ABCD
中,
AD
//
BC
,
AC
平分
BCD
。
(
1
)求证:
AD
CD
;
(
2
)若
AC
BC
,
D
120
0
,求
B
的度数。
)
(
24
、
(
6
分
)
如图是硬纸板做成的四个全等的直角三角形,两直角边长分别是
a
,
b
,斜边长为
c
,还有一个边长
为
c
的正方形,请你将它们拼成一个能证明勾股定理的图形。
(
1
)画出拼成的这个图形的示意图;
(
2
)证明勾股定理。
) (
25
、
(
8
分
)
如图,已知
ABC
中,
BD
AC
于点
D
,
CE
AB
于点
E
,
M
,
N
分别是
BC
,
DE
的中点。
(
1
)求证:
MN
DE
;
(
2
)若
BC
10
,
DE
6
,求
MDE
的面积。
) (
26
、
(
10
分
)
点
P
、
Q
分别是边长为
4
cm
的等边
ABC
的边
AB
、
BC
上的动点,点
P
从顶点
A
,点
Q
从顶点
B
同时出发,且它们的速度都是
1
cm
/
s
,设运动时间为
ts
.
(
1
)
连接
AQ
、
CP
交于点
M
,则在
P
、
Q
运动过程中,
CMQ
变化吗?若变化,则说明理由;若不变,则求
出它的度数;
(
2
)连接
PQ
,①当运动时间为多少时,
BPQ
是等边三角形,并说明理由;
) (
②
当
BPQ
为
直
角三角
形
时,
则
t
s
.
(
直
接写出
结
果)
)
(
27
、
(
10
分)
如图
1
,在
ABC
中,
AB
AC
,点
D
为射线
BC
上(
不与
B
、
C
重合
)
一动点,在
AD
的右侧射
线
BC
上方作
ADE
,使得
AD
AE
,
DAE
BAC
,连接
CE
。
(
1
)找出图中的一对全等三角形,并证明你的结论;
) (
(
2
)延长
EC
交
AB
的延长线于点
F
,若
F
45
0
,求出
DCE
的多少;
) (
(
3
)当
D
在
线
段
BC
上
时
,若线段
BC
3
,
ABC
的
面
积
为
3
,
则
四边形
ADCE
的
最
小值是
。
)
2023
2024
学年新实初二年级
10
月份月考数学试卷
一、
细心选一选,慧眼识金!(本大题共 10 小题,每小题 2 分,共 20 分)
) (
1
、下列汽车标志中,不是轴对称图形的是
) (
(
) (
)
) (
A
、
) (
B
、
) (
C
、
) (
D
、
) (
2
、到三角形三个顶点的距离相等的点是
A
、三条角平分线的交点
C
、三边上高所在直线的交点
) (
(
) (
)
) (
B
、三边中线的交点
D
、三边的垂直平分线的交点
) (
3
、若一个直角三角形的两边长分别是
12
和
5
,则第三边长的平方是
) (
(
) (
)
) (
A
、
169
) (
B
、
169
或
119
) (
C
、
13
或
15
) (
D
、
15
) (
4
、等腰三角形的一个外角是
100
0
,则它的顶角是
) (
(
) (
)
) (
A
、
20
0
) (
B
、
80
0
) (
C
、
20
0
或
80
0
) (
D
、
40
0
或
80
0
) (
5
、把一个正方形三次对折后沿虚线剪下,如图所示,则所得的图形的是
) (
(
) (
)
) (
A
、
) (
B
、
) (
C
、
) (
D
、
) (
6
、如图,
MAN
63
0
,进行如下操作:以射线
AM
上一点
B
为圆心,以线段
BA
长为半径作弧,交射线
AN
于
) (
点
C
,连接
BC
,则
BCN
的度数是
) (
(
) (
)
) (
A
、
54
0
) (
B
、
63
0
) (
C
、
117
0
) (
D
、
126
0
) (
7
、如图,直线
a
、
b
分别经过等边
ABC
的顶点,且
a
//
b
,
1
42
0
,则
2
的度数为
) (
(
) (
)
) (
A
、
18
0
) (
B
、
42
0
) (
C
、
60
0
) (
D
、
102
0
) (
第
6
题图
8
、下列语句中,正确的是
) (
第
7
题图
) (
第
9
题图
) (
(
)
B
、等腰三角形的对称轴是底边上的高
D
、等腰三角形的对称轴就是顶角平分线
) (
A
、等腰三角形底边上的中线就是底边上的垂直平分线
C
、一条线段可看作是以它的垂直平分线为对称轴的轴对称图形
9
、如图,
AD
是
ABC
的平分线,则
AB
:
AC
等于
) (
(
) (
)
) (
A
、
BD
:
CD
) (
B
、
AD
:
CD
) (
C
、
BC
:
AD
) (
D
、
BC
:
AC
)
(
10
、如图,在四边形
ABCD
中,
ABC
60
0
,
BD
平分
ABC
,
BCD
CBD
,
BC
24
,
P
、
Q
分别
) (
是
BD
、
BC
上的动点,当
CP
PQ
取得最小值时,
BQ
的长是
) (
(
) (
)
) (
A
、
8
) (
B
、
10
) (
C
、
12
) (
D
、
16
) (
第
10
题图
) (
第
11
题图
) (
第
12
题图
) (
二、
认真填一填,你一定能行!(本大题共 8 小题,每小题 3 分,共 24 分)
1
1
、如图,等腰
AB
C
的周长为
2
1
,底边
B
C
5
,
A
B
的垂直平分线
D
E
交
A
B
于点
D
,交
A
C
于点
E
,则
BE
C
的
周
长为
。
12
、
如
图,
在
ABC
中,
C
90
0
,
AD
平
分
BAC
,
CD
5
,
则
点
D
到
AB
的
距
离为
。
) (
13
、
在
ABC
中,
A
36
0
,
当
C
时,
ABC
为
等
腰三角
形
。
14
、
如
图,每
个
小正方
形
的边长
都
相等,
A
、
B
、
C
是
小
正方形
的
顶点,
则
ABC
的
度
数为
。
15
、如图,在水平桌面上依次摆着三个正方形,已知位于中间的正方形的面积为
5
,两边的正方形面积分别是
S
1
,
) (
S
2
,则
S
1
S
2
。
) (
第
14
题图
) (
第
15
题图
) (
第
16
题图
) (
16
、
如图
所
示
,
已
知
ABC
的面
积
是
36
,
OB
、
OC
分别
平
分
ABC
和
ACB
,
OD
BC
于点
D
,
为
OD
4
,
则
ABC
的
周
长是
。
17
、
AD
是
ABC
的中线,
ADB
60
0
,
BC
8
,把
ABC
沿直线
AD
折叠,使点
B
落在点
E
的位置,连接
CE
,
则
CE
的
长
为
。
) (
第
17
题图
) (
第
18
题图
) (
18
、如图,在直角
ABC
中,
C
90
0
,
AC
6
,
BC
8
,
P
、
Q
分别为
BC
、
AB
上的两个动点,若使
APQ
) (
是
等
腰三角
形
且
QPB
90
0
,则
AQ
。
)
(
三、
耐心解一解,你一定是学习的强者!(
本大题共
9
小题,共
56
分
)
19
、(
3
分)如图,
ABC
的顶点
A
、
B
、
C
都在小正方形的顶点上,
(
1
)画
A
1
B
1
C
1
,使它与
ABC
关于直线
l
对称;
(
2
)在直线
l
找一点
P
,使点
P
到点
A
、
B
的距离之和最短。
(
3
)在直线
l
找一点
Q
,使点
Q
到
AC
、
BC
的距离线段。
) (
20
、
(
4
分)
如图所示,在
3
3
的正方形网格中,已有两个正方形被涂上颜色,请再将图中剩余的
7
个小正方形
涂黑一个,使整个图案成为一个轴对称图形。
(
请用
4
种不同的方法涂
)
) (
21
、(
4
分)已知,如图在
ABC
中,
AB
AC
,点
M
、
N
在
BC
上,且
AM
AN
,求证:
BM
CN
.
) (
22
、
(
5
分
)
如图,在
ABC
中,
ACB
90
0
,
AD
平分
BAC
,
DE
AB
于点
E
。
求证:直线
AD
是线段
CE
的垂直平分线。
) (
23
、(
6
分)如图,在四边形
ABCD
中,
AD
//
BC
,
AC
平分
BCD
。
(
1
)求证:
AD
CD
;
(
2
)若
AC
BC
,
D
120
0
,求
B
的度数。
)
(
24
、
(
6
分
)
如图是硬纸板做成的四个全等的直角三角形,两直角边长分别是
a
,
b
,斜边长为
c
,还有一个边长
为
c
的正方形,请你将它们拼成一个能证明勾股定理的图形。
(
1
)画出拼成的这个图形的示意图;
(
2
)证明勾股定理。
) (
25
、
(
8
分
)
如图,已知
ABC
中,
BD
AC
于点
D
,
CE
AB
于点
E
,
M
,
N
分别是
BC
,
DE
的中点。
(
1
)求证:
MN
DE
;
(
2
)若
BC
10
,
DE
6
,求
MDE
的面积。
) (
26
、
(
10
分
)
点
P
、
Q
分别是边长为
4
cm
的等边
ABC
的边
AB
、
BC
上的动点,点
P
从顶点
A
,点
Q
从顶点
B
同时出发,且它们的速度都是
1
cm
/
s
,设运动时间为
ts
.
(
1
)
连接
AQ
、
CP
交于点
M
,则在
P
、
Q
运动过程中,
CMQ
变化吗?若变化,则说明理由;若不变,则求
出它的度数;
(
2
)连接
PQ
,①当运动时间为多少时,
BPQ
是等边三角形,并说明理由;
) (
②
当
BPQ
为
直
角三角
形
时,
则
t
s
.
(
直
接写出
结
果)
)
(
27
、
(
10
分)
如图
1
,在
ABC
中,
AB
AC
,点
D
为射线
BC
上(
不与
B
、
C
重合
)
一动点,在
AD
的右侧射
线
BC
上方作
ADE
,使得
AD
AE
,
DAE
BAC
,连接
CE
。
(
1
)找出图中的一对全等三角形,并证明你的结论;
) (
(
2
)延长
EC
交
AB
的延长线于点
F
,若
F
45
0
,求出
DCE
的多少;
) (
(
3
)当
D
在
线
段
BC
上
时
,若线段
BC
3
,
ABC
的
面
积
为
3
,
则
四边形
ADCE
的
最
小值是
。
)
同课章节目录
