2023~2024学年北京市西城区第44中初二上数学阶段性学情调研(无答案)
文档属性
| 名称 | 2023~2024学年北京市西城区第44中初二上数学阶段性学情调研(无答案) | 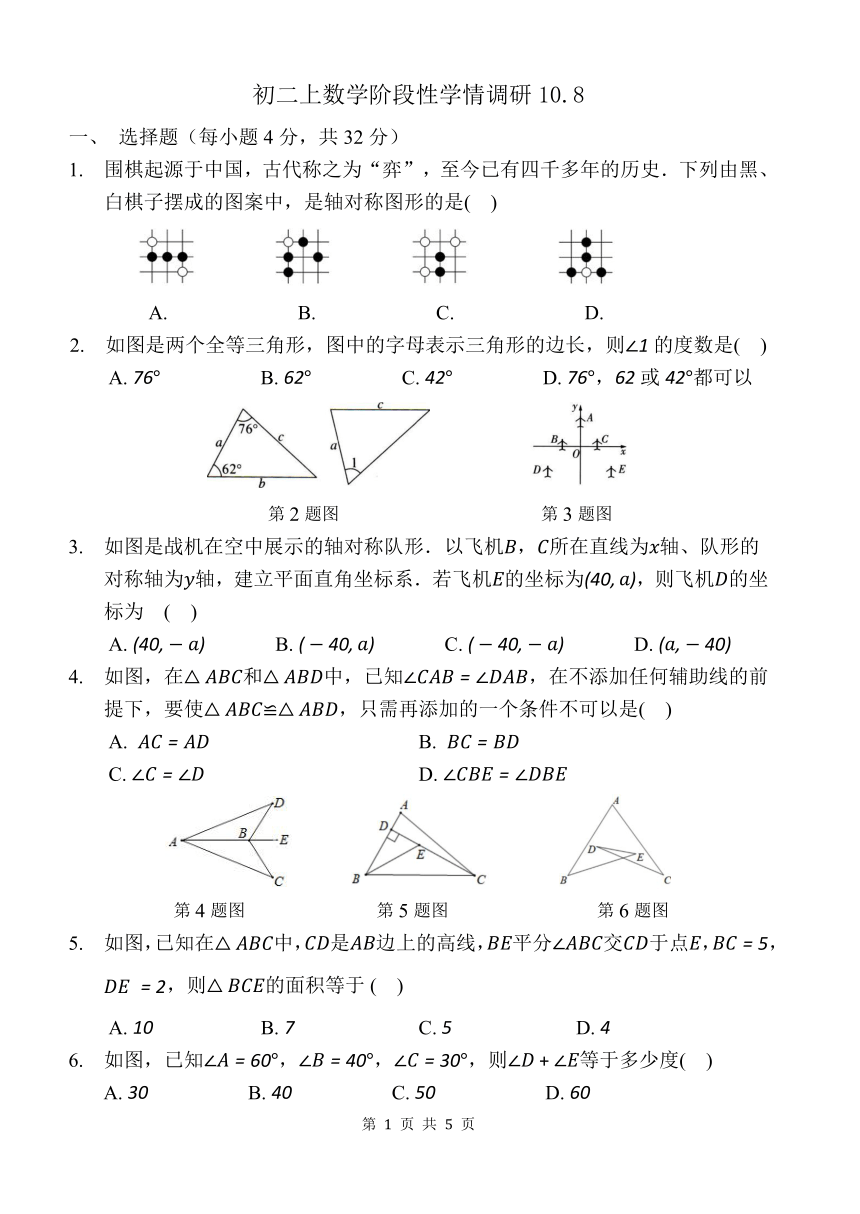 | |
| 格式 | |||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-12 18:00:16 | ||
图片预览


文档简介
初二上数学阶段性学情调研 10.8
一、 选择题(每小题 4分,共 32分)
1. 围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史.下列由黑、
白棋子摆成的图案中,是轴对称图形的是( )
A. B. C. D.
2. 如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
A. 76° B. 62° C. 42° D. 76°,62或 42°都可以
第 2 题图 第 3 题图
3. 如图是战机在空中展示的轴对称队形.以飞机 , 所在直线为 轴、队形的
对称轴为 轴,建立平面直角坐标系.若飞机 的坐标为(40, ),则飞机 的坐
标为 ( )
A. (40, ) B. ( 40, ) C. ( 40, ) D. ( , 40)
4. 如图,在△ 和△ 中,已知∠ = ∠ ,在不添加任何辅助线的前
提下,要使△ ≌△ ,只需再添加的一个条件不可以是( )
A. = B. =
C. ∠ = ∠ D. ∠ = ∠
第 4 题图 第 5 题图 第 6 题图
5. 如图,已知在△ 中, 是 边上的高线, 平分∠ 交 于点 , = 5,
= 2,则△ 的面积等于 ( )
A. 10 B. 7 C. 5 D. 4
6. 如图,已知∠ = 60°,∠ = 40°,∠ = 30°,则∠ + ∠ 等于多少度( )
A. 30 B. 40 C. 50 D. 60
第 1 页 共 5 页
7. 如图, 垂直平分 , 垂直平分 ,若 的长为 7,则 的长为( )
A. 5 B. 6 C. 7 D. 8
第 7 题图 第 8 题图
8. 如图,在 △ 中, = 6, = 8, = 10.点 从点 出发,以每秒 2
个单位长度的速度沿折线 向终点 运动,同时点 从点 出发,以每
秒 3个单位长度的速度沿折线 向终点 运动,点 , 都运动到各自
的终点时停止.设运动时间为 (秒),直线 经过点 ,且 // ,过点 , 分别
作直线 的垂线段,垂足为 , .
当△ 与△ 全等时, 的值不可能是( )
A. 2 B. 2.8 C. 3 D. 6
二、 填空题(每小题 3分,共 24分)
9. 如图,公园里有一座假山,要测量假山两端 、 的距离,先在平地上取一个
可以直接到达 、 的点 ,分别延长 、 ,到 、 ,使 = , = ,
连接 ,这样就可以利用三角形全等,通过测量 的长得到假山两端 、
的距离,则这两个三角形全等的依据是______.
第 9 题图 第 10 题图 第 11 题图
10. 在正方形网格中,∠AOB 的位置如图所示,到∠AOB 两边距离相等的点应是___.
11. 图(1)是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并
开始消融,形状无一定规则,代表一种自然和谐美,图(2)是从图(1)冰裂纹窗
格图案中提取的由五条线段组成的图形,则∠1 + ∠2 + ∠3 + ∠4 + ∠5 = °.
12. 如图,在△ 中,∠ = ∠ = 50 , = , = ,
则∠ 的度数是______.
第 2 页 共 5 页
13. 如图,在△ 中, = 6, = 8, = 11, 的垂直平分线分别交 ,
于点 、 , 的垂直平分线分别交 , 于点 、 ,则△ 的周长为
______.
第 13 题图 第 14 题图 第 15 题图
14. 如图,在△ 中,∠ = 40°,∠ = 30°, 为边 上一点,将△ 沿直线
翻折后,点 落到点 处.若 // ,则∠ 的度数为 .
15. 如图,在平面直角坐标系中,将直角三角形的直角顶点放在点 (4,4)处,两直
角边分别与坐标轴交于点 和点 ,则 + 的值为_________.
16. 程老师制作了如图1所示的学具,用来探究“边边角条件是否可确定三角形 的
形状”问题.操作学具时,点 Q在轨道槽 AM上运动,点 P既能在以 A为圆心,
以 8为半径的半圆轨道槽上运动,也能在轨道槽 QN上运动.图 2是操作学具
时,所对应某个位置的图形的示意图.
图 2
图 1
①当 PAQ = 30°,PQ=6 时,可得到形状唯一确定的△PAQ
②当 PAQ = 30°,PQ=9 时,可得到形状唯一确定的△PAQ
③当 PAQ = 90°,PQ=10 时,可得到形状唯一确定的△PAQ
④当 PAQ = 150°,PQ=12 时,可得到形状唯一确定的△PAQ
以上结论正确的是 .
三、 解答题(共 44分)
17. 下面是小东设计的尺规作图过程.
已知:如图,在 △ 中,∠ = 90°,
求作:点 ,使点 在 边上,且到 和 的距离相等.
作法:
第 3 页 共 5 页
①如图,以点 为圆心,任意长为半径画弧,分别交 , 于点 、 ;
1
②分别以点 , 为圆心,大于 的长为半径画弧,两弧交于点 ;
2
③画射线 ,交 于点 .
所以点 即为所求.
根据小东设计的尺规作图过程:
(1) 使用直尺和圆规,补全图形(保留作图痕迹);
(2) 完成下面的证明.
证明:过点 作 ⊥ 于点 ,连接 , .
在△ 与△ 中,
∵ = , = , = ,
∴△ ≌△ ( ).
∴ ∠______= ∠______.
∵ ∠ = 90°,
∴ ⊥ .
又∵ ⊥ ,
∴ = ( ).
18. 如图,在△ 中,
(1) 尺规作图:作边 的垂直平分线,交 于点 ,交 于点 ,连结 .
(2) 若△ 的周长等于 18, = 4,求△ 的周长.
19. 如图,在四边形 中, // , 为 的中点,连接 并延长交 的延
长线于点 .
(1) 求证 = .
(2) 若 = 2, = 8,当 的长为多少时,点 在线段 的垂直平分线上?
说明原因.
第 4 页 共 5 页
20. 如图,四边形 中, = , = ,我们把这种两组邻边分别相等
的四边形叫做“筝形”,
(1) 求证:△ ≌△ ;
(2) 测量 与 、∠ 与∠ ,你有何猜想?证明你的猜想.
21. 如图,在△ 中,∠ = 90 , 为 边上一点, 平分∠ ,且 = ,
若 = 2, = 3,求 的长.
22. 四边形ABCD 是正方形,△BEF 是等腰直角三角形,∠BEF=90°, BE=EF.
点 G 为DF 的中点,连接EG ,CG ,EC.
(1)如图 1,若点E 在 CB 边的延长线上,直接写出EG 与 GC 的数量关系和
位置关系;
(2)将图 1 中的△BEF 绕点B 顺时针方向旋转至图 2所示位置,(1)中所得的
结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;
第 5 页 共 5 页
一、 选择题(每小题 4分,共 32分)
1. 围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史.下列由黑、
白棋子摆成的图案中,是轴对称图形的是( )
A. B. C. D.
2. 如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
A. 76° B. 62° C. 42° D. 76°,62或 42°都可以
第 2 题图 第 3 题图
3. 如图是战机在空中展示的轴对称队形.以飞机 , 所在直线为 轴、队形的
对称轴为 轴,建立平面直角坐标系.若飞机 的坐标为(40, ),则飞机 的坐
标为 ( )
A. (40, ) B. ( 40, ) C. ( 40, ) D. ( , 40)
4. 如图,在△ 和△ 中,已知∠ = ∠ ,在不添加任何辅助线的前
提下,要使△ ≌△ ,只需再添加的一个条件不可以是( )
A. = B. =
C. ∠ = ∠ D. ∠ = ∠
第 4 题图 第 5 题图 第 6 题图
5. 如图,已知在△ 中, 是 边上的高线, 平分∠ 交 于点 , = 5,
= 2,则△ 的面积等于 ( )
A. 10 B. 7 C. 5 D. 4
6. 如图,已知∠ = 60°,∠ = 40°,∠ = 30°,则∠ + ∠ 等于多少度( )
A. 30 B. 40 C. 50 D. 60
第 1 页 共 5 页
7. 如图, 垂直平分 , 垂直平分 ,若 的长为 7,则 的长为( )
A. 5 B. 6 C. 7 D. 8
第 7 题图 第 8 题图
8. 如图,在 △ 中, = 6, = 8, = 10.点 从点 出发,以每秒 2
个单位长度的速度沿折线 向终点 运动,同时点 从点 出发,以每
秒 3个单位长度的速度沿折线 向终点 运动,点 , 都运动到各自
的终点时停止.设运动时间为 (秒),直线 经过点 ,且 // ,过点 , 分别
作直线 的垂线段,垂足为 , .
当△ 与△ 全等时, 的值不可能是( )
A. 2 B. 2.8 C. 3 D. 6
二、 填空题(每小题 3分,共 24分)
9. 如图,公园里有一座假山,要测量假山两端 、 的距离,先在平地上取一个
可以直接到达 、 的点 ,分别延长 、 ,到 、 ,使 = , = ,
连接 ,这样就可以利用三角形全等,通过测量 的长得到假山两端 、
的距离,则这两个三角形全等的依据是______.
第 9 题图 第 10 题图 第 11 题图
10. 在正方形网格中,∠AOB 的位置如图所示,到∠AOB 两边距离相等的点应是___.
11. 图(1)是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并
开始消融,形状无一定规则,代表一种自然和谐美,图(2)是从图(1)冰裂纹窗
格图案中提取的由五条线段组成的图形,则∠1 + ∠2 + ∠3 + ∠4 + ∠5 = °.
12. 如图,在△ 中,∠ = ∠ = 50 , = , = ,
则∠ 的度数是______.
第 2 页 共 5 页
13. 如图,在△ 中, = 6, = 8, = 11, 的垂直平分线分别交 ,
于点 、 , 的垂直平分线分别交 , 于点 、 ,则△ 的周长为
______.
第 13 题图 第 14 题图 第 15 题图
14. 如图,在△ 中,∠ = 40°,∠ = 30°, 为边 上一点,将△ 沿直线
翻折后,点 落到点 处.若 // ,则∠ 的度数为 .
15. 如图,在平面直角坐标系中,将直角三角形的直角顶点放在点 (4,4)处,两直
角边分别与坐标轴交于点 和点 ,则 + 的值为_________.
16. 程老师制作了如图1所示的学具,用来探究“边边角条件是否可确定三角形 的
形状”问题.操作学具时,点 Q在轨道槽 AM上运动,点 P既能在以 A为圆心,
以 8为半径的半圆轨道槽上运动,也能在轨道槽 QN上运动.图 2是操作学具
时,所对应某个位置的图形的示意图.
图 2
图 1
①当 PAQ = 30°,PQ=6 时,可得到形状唯一确定的△PAQ
②当 PAQ = 30°,PQ=9 时,可得到形状唯一确定的△PAQ
③当 PAQ = 90°,PQ=10 时,可得到形状唯一确定的△PAQ
④当 PAQ = 150°,PQ=12 时,可得到形状唯一确定的△PAQ
以上结论正确的是 .
三、 解答题(共 44分)
17. 下面是小东设计的尺规作图过程.
已知:如图,在 △ 中,∠ = 90°,
求作:点 ,使点 在 边上,且到 和 的距离相等.
作法:
第 3 页 共 5 页
①如图,以点 为圆心,任意长为半径画弧,分别交 , 于点 、 ;
1
②分别以点 , 为圆心,大于 的长为半径画弧,两弧交于点 ;
2
③画射线 ,交 于点 .
所以点 即为所求.
根据小东设计的尺规作图过程:
(1) 使用直尺和圆规,补全图形(保留作图痕迹);
(2) 完成下面的证明.
证明:过点 作 ⊥ 于点 ,连接 , .
在△ 与△ 中,
∵ = , = , = ,
∴△ ≌△ ( ).
∴ ∠______= ∠______.
∵ ∠ = 90°,
∴ ⊥ .
又∵ ⊥ ,
∴ = ( ).
18. 如图,在△ 中,
(1) 尺规作图:作边 的垂直平分线,交 于点 ,交 于点 ,连结 .
(2) 若△ 的周长等于 18, = 4,求△ 的周长.
19. 如图,在四边形 中, // , 为 的中点,连接 并延长交 的延
长线于点 .
(1) 求证 = .
(2) 若 = 2, = 8,当 的长为多少时,点 在线段 的垂直平分线上?
说明原因.
第 4 页 共 5 页
20. 如图,四边形 中, = , = ,我们把这种两组邻边分别相等
的四边形叫做“筝形”,
(1) 求证:△ ≌△ ;
(2) 测量 与 、∠ 与∠ ,你有何猜想?证明你的猜想.
21. 如图,在△ 中,∠ = 90 , 为 边上一点, 平分∠ ,且 = ,
若 = 2, = 3,求 的长.
22. 四边形ABCD 是正方形,△BEF 是等腰直角三角形,∠BEF=90°, BE=EF.
点 G 为DF 的中点,连接EG ,CG ,EC.
(1)如图 1,若点E 在 CB 边的延长线上,直接写出EG 与 GC 的数量关系和
位置关系;
(2)将图 1 中的△BEF 绕点B 顺时针方向旋转至图 2所示位置,(1)中所得的
结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;
第 5 页 共 5 页
同课章节目录
