第二十二章 二次函数 单元练习(含答案) 2023—2024学年人教版数学九年级上册
文档属性
| 名称 | 第二十二章 二次函数 单元练习(含答案) 2023—2024学年人教版数学九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 70.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-13 00:00:00 | ||
图片预览


文档简介
第二十二章 二次函数
一、选择题
1.下列函数中,是二次函数的是( )
A.y=3x﹣2 B.y=
C.y=x2+1 D.y=(x﹣1)2﹣x2
2.抛物线的顶点坐标是( )
A. B. C. D.
3.将抛物线先向右平移3个单位长度,再向上平移2个单位长度,平移后抛物线的顶点坐标是( )
A. B. C. D.
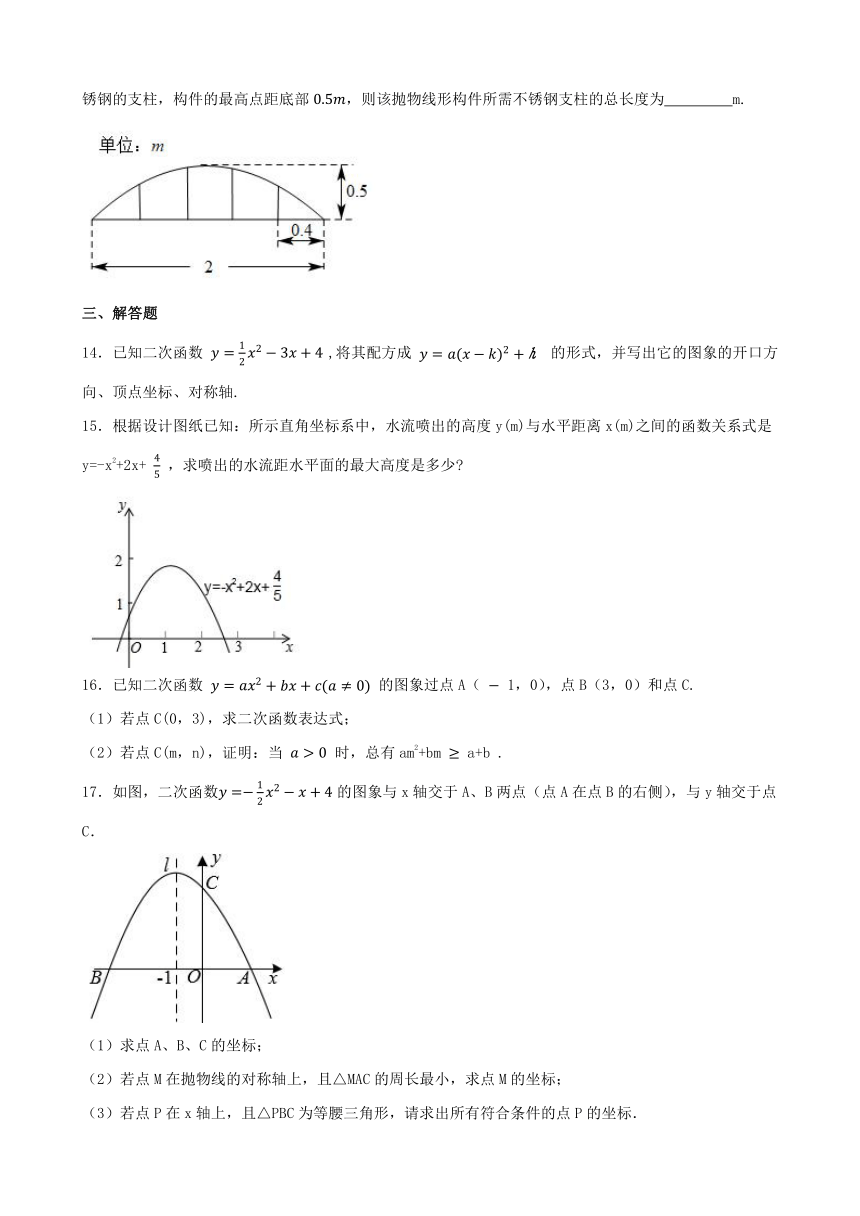
4. 如图,在同一平面直角坐标系中,二次函数与一次函数的图象可能是( )
A. B.
C. D.
5.已知二次函数的图象(0≤x≤3)如图所示,下列关于该函数在所给自变量取值范围内的说法正确的是( )
A.有最小值0,最大值3 B.有最小值﹣1,最大值3
C.有最小值﹣1,最大值0 D.有最小值﹣1,无最大值
6.如图,以直线 为对称轴的二次函数 的图象与x轴负半轴交于A点,则一元二次方程 的正数解的范围是( )
A. B. C. D.
7.某商品的进价为每件20元,现在的售价为每件40元,每星期可卖出200件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出5件.则每星期售出商品的利润y(单位:元)与每件涨价x(单位:元)之间的函数关系式是( )
A.y=(200﹣5x)(40﹣20+x) B.y=(200+5x)(40﹣20﹣x)
C.y=200(40﹣20﹣x) D.y=200﹣5x
8.已知二次函数 的图象如图所示,则下列结论:① ;② ;③当 时, :④方程 有两个大于-1的实数根.其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①③④
二、填空题
9.已知函数,当x 时,y随x的增大而增大.
10.已知函数的图象与x轴有且仅有一个交点,则k的值为 .
11.已知二次函数y=﹣x2+2mx+1,当﹣2≤x≤1时最大值为4,则m的值为 .
12.已知二次函数 的部分图象如图所示,则关于x的一元二次方程 的解为 .
13.如图所示的抛物线形构件为某工业园区的新厂房骨架,为了牢固起见,构件需要每隔加设一根不锈钢的支柱,构件的最高点距底部,则该抛物线形构件所需不锈钢支柱的总长度为 m.
三、解答题
14.已知二次函数 ,将其配方成 的形式,并写出它的图象的开口方向、顶点坐标、对称轴.
15.根据设计图纸已知:所示直角坐标系中,水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是y=-x2+2x+ ,求喷出的水流距水平面的最大高度是多少
16.已知二次函数 的图象过点A( 1,0),点B(3,0)和点C.
(1)若点C(0,3),求二次函数表达式;
(2)若点C(m,n),证明:当 时,总有am2+bm a+b .
17.如图,二次函数的图象与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C.
(1)求点A、B、C的坐标;
(2)若点M在抛物线的对称轴上,且△MAC的周长最小,求点M的坐标;
(3)若点P在x轴上,且△PBC为等腰三角形,请求出所有符合条件的点P的坐标.
18.“互联网+”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条60元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售10条.设每条裤子的售价为x元(x为正整数),每月的销售量为y条.
(1)直接写出y与x的函数关系式;
(2)设该网店每月获得的利润为w元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少
(3)该网店店主热心公益事业,决定每月从利润中捐出500元资助贫困学生.为了保证捐款后每月利润不低于1590元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价
参考答案
1.C
2.D
3.C
4.B
5.B
6.C
7.A
8.B
9.
10.2或3
11.﹣或2
12. , .
13.1.6
14.解:
开口方向向上
顶点坐标是
对称轴是直线
15.解: 当 时,
有最大值=
喷出的水流距水平面的最大高度时 。
当 时, 有最大值
答:喷出的水流距水平面的最大高度时 。
16.(1)解:设y=a(x+1)(x-3),代入点C (0,3)
解得a=-1
∴y=-(x+1)(x-3)
(2)解:方法一:∵图像过A(-1,0),点B(3,0),∴对称轴为直线x=1
a>0,当x=1时,图像有最小值,此时最小值为y=a+b+c
∴当x=m时,存在am2+bm+c≥a+b+c.
∴am2+bm≥a+b
方法二:∵图像过A(-1,0),点B(3,0),∴ ,则b=-2a.
am2+bm- a-b= am2-2am-a+2a= am2-2am+a=a(m2-2m+1)=a(m-1)2≥0
∴am2+bm≥a+b.
17.(1)解:令
解得,
∴A , B
令,得,
∴C
∴点A的坐标为,点B的坐标为,点C的坐标为
(2)解:如图,过点C作对称轴l,与抛物线交于点E,连接AE交l于点M
∵点C与点E关于直线l对称,点M在对称轴l上
∴,
∴△MAC的周长
∴当且仅当E、M、A三点共线时,△MAC的周长最小
设直线AE的解析式为,
将坐标代入得
解得
∴直线AE的解析式为
令,得
∴点M坐标为.
(3)解:设P点的坐标为
∵,
∴,,
当△PBC是等腰三角形时,分三种情况求解:
①当时,由题意可得
解得
∴P的坐标为;
②当时,由题意可得
解得或
∴P的坐标为或;
③当时,由题意可得
解得或(不合题意,舍去)
∴P的坐标为;
综上所述,P点的坐标为 或 或 或.
18.(1)解:
(2)解:
∵抛物线开口向下∴当时,元
答:当销售价格为75元时,每月获得利润最大为2250元
(3)解:由题意得:
解得:为了让消费者得到最大的实惠,故
一、选择题
1.下列函数中,是二次函数的是( )
A.y=3x﹣2 B.y=
C.y=x2+1 D.y=(x﹣1)2﹣x2
2.抛物线的顶点坐标是( )
A. B. C. D.
3.将抛物线先向右平移3个单位长度,再向上平移2个单位长度,平移后抛物线的顶点坐标是( )
A. B. C. D.
4. 如图,在同一平面直角坐标系中,二次函数与一次函数的图象可能是( )
A. B.
C. D.
5.已知二次函数的图象(0≤x≤3)如图所示,下列关于该函数在所给自变量取值范围内的说法正确的是( )
A.有最小值0,最大值3 B.有最小值﹣1,最大值3
C.有最小值﹣1,最大值0 D.有最小值﹣1,无最大值
6.如图,以直线 为对称轴的二次函数 的图象与x轴负半轴交于A点,则一元二次方程 的正数解的范围是( )
A. B. C. D.
7.某商品的进价为每件20元,现在的售价为每件40元,每星期可卖出200件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出5件.则每星期售出商品的利润y(单位:元)与每件涨价x(单位:元)之间的函数关系式是( )
A.y=(200﹣5x)(40﹣20+x) B.y=(200+5x)(40﹣20﹣x)
C.y=200(40﹣20﹣x) D.y=200﹣5x
8.已知二次函数 的图象如图所示,则下列结论:① ;② ;③当 时, :④方程 有两个大于-1的实数根.其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①③④
二、填空题
9.已知函数,当x 时,y随x的增大而增大.
10.已知函数的图象与x轴有且仅有一个交点,则k的值为 .
11.已知二次函数y=﹣x2+2mx+1,当﹣2≤x≤1时最大值为4,则m的值为 .
12.已知二次函数 的部分图象如图所示,则关于x的一元二次方程 的解为 .
13.如图所示的抛物线形构件为某工业园区的新厂房骨架,为了牢固起见,构件需要每隔加设一根不锈钢的支柱,构件的最高点距底部,则该抛物线形构件所需不锈钢支柱的总长度为 m.
三、解答题
14.已知二次函数 ,将其配方成 的形式,并写出它的图象的开口方向、顶点坐标、对称轴.
15.根据设计图纸已知:所示直角坐标系中,水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是y=-x2+2x+ ,求喷出的水流距水平面的最大高度是多少
16.已知二次函数 的图象过点A( 1,0),点B(3,0)和点C.
(1)若点C(0,3),求二次函数表达式;
(2)若点C(m,n),证明:当 时,总有am2+bm a+b .
17.如图,二次函数的图象与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C.
(1)求点A、B、C的坐标;
(2)若点M在抛物线的对称轴上,且△MAC的周长最小,求点M的坐标;
(3)若点P在x轴上,且△PBC为等腰三角形,请求出所有符合条件的点P的坐标.
18.“互联网+”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条60元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售10条.设每条裤子的售价为x元(x为正整数),每月的销售量为y条.
(1)直接写出y与x的函数关系式;
(2)设该网店每月获得的利润为w元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少
(3)该网店店主热心公益事业,决定每月从利润中捐出500元资助贫困学生.为了保证捐款后每月利润不低于1590元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价
参考答案
1.C
2.D
3.C
4.B
5.B
6.C
7.A
8.B
9.
10.2或3
11.﹣或2
12. , .
13.1.6
14.解:
开口方向向上
顶点坐标是
对称轴是直线
15.解: 当 时,
有最大值=
喷出的水流距水平面的最大高度时 。
当 时, 有最大值
答:喷出的水流距水平面的最大高度时 。
16.(1)解:设y=a(x+1)(x-3),代入点C (0,3)
解得a=-1
∴y=-(x+1)(x-3)
(2)解:方法一:∵图像过A(-1,0),点B(3,0),∴对称轴为直线x=1
a>0,当x=1时,图像有最小值,此时最小值为y=a+b+c
∴当x=m时,存在am2+bm+c≥a+b+c.
∴am2+bm≥a+b
方法二:∵图像过A(-1,0),点B(3,0),∴ ,则b=-2a.
am2+bm- a-b= am2-2am-a+2a= am2-2am+a=a(m2-2m+1)=a(m-1)2≥0
∴am2+bm≥a+b.
17.(1)解:令
解得,
∴A , B
令,得,
∴C
∴点A的坐标为,点B的坐标为,点C的坐标为
(2)解:如图,过点C作对称轴l,与抛物线交于点E,连接AE交l于点M
∵点C与点E关于直线l对称,点M在对称轴l上
∴,
∴△MAC的周长
∴当且仅当E、M、A三点共线时,△MAC的周长最小
设直线AE的解析式为,
将坐标代入得
解得
∴直线AE的解析式为
令,得
∴点M坐标为.
(3)解:设P点的坐标为
∵,
∴,,
当△PBC是等腰三角形时,分三种情况求解:
①当时,由题意可得
解得
∴P的坐标为;
②当时,由题意可得
解得或
∴P的坐标为或;
③当时,由题意可得
解得或(不合题意,舍去)
∴P的坐标为;
综上所述,P点的坐标为 或 或 或.
18.(1)解:
(2)解:
∵抛物线开口向下∴当时,元
答:当销售价格为75元时,每月获得利润最大为2250元
(3)解:由题意得:
解得:为了让消费者得到最大的实惠,故
同课章节目录
