第22章 二次函数 单元综合训练(无答案)2023—2024学年人教版数学九年级上册
文档属性
| 名称 | 第22章 二次函数 单元综合训练(无答案)2023—2024学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 332.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-13 00:00:00 | ||
图片预览

文档简介
第22章 二次函数 单元综合训练
一、单选题
1.下列函数是二次函数的是( )
A.y=2x+1 B.y=﹣2x+1 C.y=x2+2 D.y=x﹣2
2.二次函数的图象的顶点坐标是( )
A.(1,3) B.(,3) C.(1,) D.(,)
3.若将抛物线向右平移3个单位,再向上平移5个单位,则得到的抛物线是 ( )
A. B.
C. D.
4.已知,点 ,,都在函数的图象上,则( )
A. B. C. D.
5.如图,在同一平面直角坐标系中,函数与的图象可能是( )
A.B.C.D.
6.已知二次函数y=ax2+bx+c的x与y的部分对应值如下表:
x -1 0 1 2 3
y 5 1 -1 -1 1
则该二次函数图象的对称轴为( )
A.y轴 B.直线x= C.直线x=2 D.直线x=
7.老师出示了小黑板上的题后(如图),小华说:过点(3,0);小彬说:过点(4,3);小明说:a=1;小颖说:抛物线被x轴截得的线段长为2.你认为四人的说法中,正确的有( )
A.1个 B.2个 C.3个 D.4个
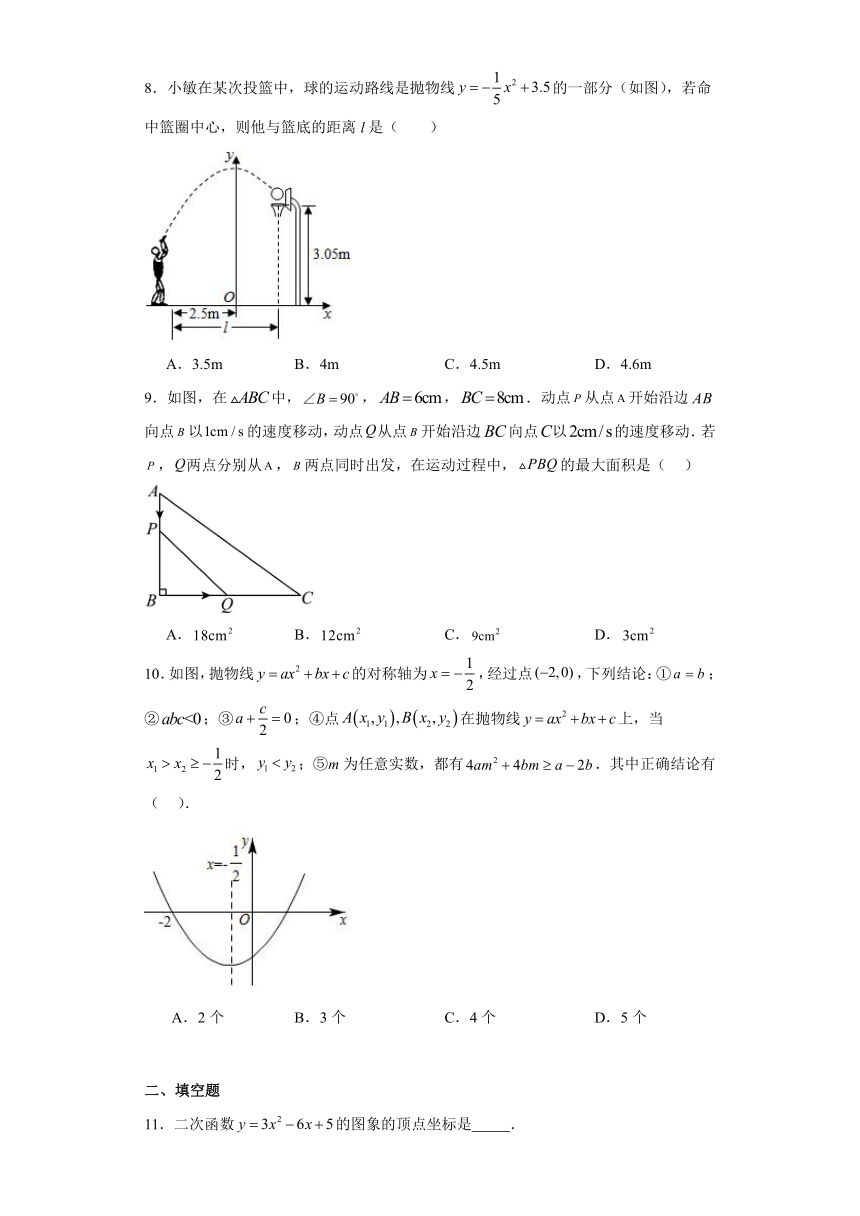
8.小敏在某次投篮中,球的运动路线是抛物线的一部分(如图),若命中篮圈中心,则他与篮底的距离l是( )
A.3.5m B.4m C.4.5m D.4.6m
9.如图,在中,,,.动点从点开始沿边向点以的速度移动,动点从点开始沿边向点以的速度移动.若,两点分别从,两点同时出发,在运动过程中,的最大面积是( )
A. B. C. D.
10.如图,抛物线的对称轴为,经过点,下列结论:①;②;③;④点在抛物线上,当时,;⑤m为任意实数,都有.其中正确结论有( ).
A.2个 B.3个 C.4个 D.5个
二、填空题
11.二次函数的图象的顶点坐标是 .
12.关于x的函数是二次函数,则m= .
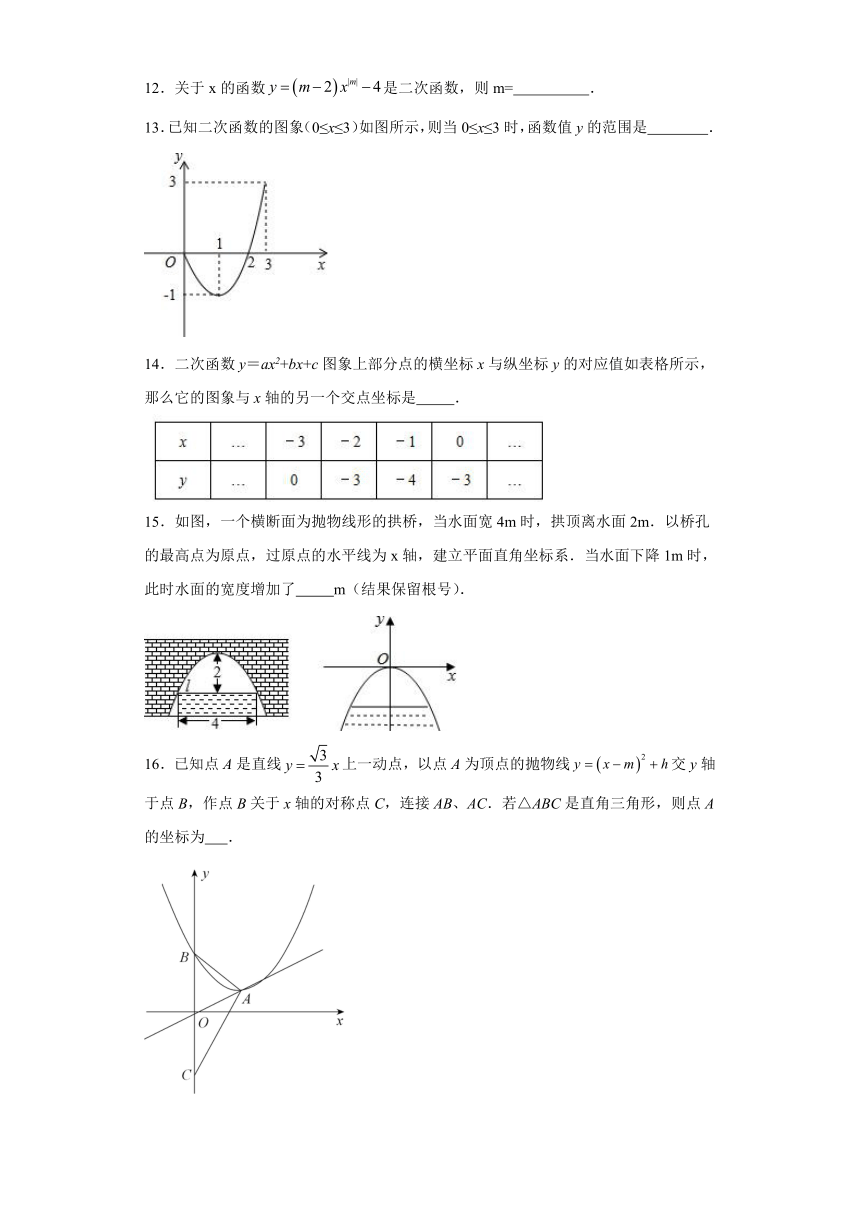
13.已知二次函数的图象(0≤x≤3)如图所示,则当0≤x≤3时,函数值y的范围是 .
14.二次函数y=ax2+bx+c图象上部分点的横坐标x与纵坐标y的对应值如表格所示,那么它的图象与x轴的另一个交点坐标是 .
15.如图,一个横断面为抛物线形的拱桥,当水面宽4m时,拱顶离水面2m.以桥孔的最高点为原点,过原点的水平线为x轴,建立平面直角坐标系.当水面下降1m时,此时水面的宽度增加了 m(结果保留根号).
16.已知点A是直线上一动点,以点A为顶点的抛物线交y轴于点B,作点B关于x轴的对称点C,连接AB、AC.若△ABC是直角三角形,则点A的坐标为 .
三、解答题
17.根据下列条件,分别求出二次函数的解析式.
(1)已知图象的顶点坐标为(﹣1,﹣8),且过点(0,﹣6);
(2)已知图象经过点A(﹣1,0)、B(0,3),且对称轴为直线x=1.
18.已知抛物线.
(1)写出它的开口方向、对称轴和顶点坐标;
(2)当为何值时,函数取得最大值,请求出这个最大值.
19.如图,利用一面墙(墙长10米)用20米的篱笆国成一个矩形场地.设垂直于墙的一边为x米.矩形场地的面积为s平方米.
(1)求s与x的函数关系式,并求出x的取值范围;
(2)若矩形场地的面积最大,应该如何设计长与宽.
20.如图,二次函数的图象与y交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数的图象经过该二次函数图象上的点及点B.
(1)求二次函数与一次函数的表达式.
(2)根据图象,写出满足的x的取值范围.
21.果园有果树60棵,现准备多种一些果树提高果园产量.如果多种树,那么树之间的距离和每棵果树所受光照就会减少,每棵果树的平均产量随之降低.根据经验,增种10棵果树时,果园内的每棵果树平均产量为75kg.在确保每棵果树平均产量不低于40kg的前提下,设增种果树(且为整数)棵,该果园每棵果树平均产量为kg,它们之间的函数关系满足如图所示的图像.
(1)每增种1棵果树时,每棵果树平均产量减少______kg;
(2)求与之间的函数关系式,并直接写出自变量的取值范围;
(3)当增种果树多少棵时,果园的总产量(kg)最大?最大产量是多少?
22.如图,已知抛物线经过A(-1,0),B(3,0)两点.
(1)求抛物线的解析式;
(2)当0(3)点P为抛物线上一点,若,求出此时点P的坐标.
23.如图1是一座抛物线型拱桥侧面示意图.水面宽AB与桥长CD均为24m,在距离D点6米的E处,测得桥面到桥拱的距离EF为1.5m,以桥拱顶点O为原点,桥面为x轴建立平面直角坐标系.
(1)求桥拱项部O离水面的距离.
(2)如图2,桥面上方有3根高度均为4m的支柱CG,OH,DI,过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面距离为1m.
①求出其中一条钢缆抛物线的函数表达式.
②为庆祝节日,在钢缆和桥拱之间竖直装饰若干条彩带,求彩带长度的最小值.
24.如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,﹣1),且与y轴交于点C(0,3),与x轴交于A、B两点(点A在点B的右侧),点P是抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点 D.
(1)求该抛物线的函数关系式及A、B两点的坐标;
(2)求点P在运动的过程中,线段PD的最大值;
(3)若点P与点Q重合,点E在x轴上,点F在抛物线上,问是否存在以A,P,E,F为顶点的平行四边形?若存在,直接写出点F的坐标;若不存在,请说明理由.
一、单选题
1.下列函数是二次函数的是( )
A.y=2x+1 B.y=﹣2x+1 C.y=x2+2 D.y=x﹣2
2.二次函数的图象的顶点坐标是( )
A.(1,3) B.(,3) C.(1,) D.(,)
3.若将抛物线向右平移3个单位,再向上平移5个单位,则得到的抛物线是 ( )
A. B.
C. D.
4.已知,点 ,,都在函数的图象上,则( )
A. B. C. D.
5.如图,在同一平面直角坐标系中,函数与的图象可能是( )
A.B.C.D.
6.已知二次函数y=ax2+bx+c的x与y的部分对应值如下表:
x -1 0 1 2 3
y 5 1 -1 -1 1
则该二次函数图象的对称轴为( )
A.y轴 B.直线x= C.直线x=2 D.直线x=
7.老师出示了小黑板上的题后(如图),小华说:过点(3,0);小彬说:过点(4,3);小明说:a=1;小颖说:抛物线被x轴截得的线段长为2.你认为四人的说法中,正确的有( )
A.1个 B.2个 C.3个 D.4个
8.小敏在某次投篮中,球的运动路线是抛物线的一部分(如图),若命中篮圈中心,则他与篮底的距离l是( )
A.3.5m B.4m C.4.5m D.4.6m
9.如图,在中,,,.动点从点开始沿边向点以的速度移动,动点从点开始沿边向点以的速度移动.若,两点分别从,两点同时出发,在运动过程中,的最大面积是( )
A. B. C. D.
10.如图,抛物线的对称轴为,经过点,下列结论:①;②;③;④点在抛物线上,当时,;⑤m为任意实数,都有.其中正确结论有( ).
A.2个 B.3个 C.4个 D.5个
二、填空题
11.二次函数的图象的顶点坐标是 .
12.关于x的函数是二次函数,则m= .
13.已知二次函数的图象(0≤x≤3)如图所示,则当0≤x≤3时,函数值y的范围是 .
14.二次函数y=ax2+bx+c图象上部分点的横坐标x与纵坐标y的对应值如表格所示,那么它的图象与x轴的另一个交点坐标是 .
15.如图,一个横断面为抛物线形的拱桥,当水面宽4m时,拱顶离水面2m.以桥孔的最高点为原点,过原点的水平线为x轴,建立平面直角坐标系.当水面下降1m时,此时水面的宽度增加了 m(结果保留根号).
16.已知点A是直线上一动点,以点A为顶点的抛物线交y轴于点B,作点B关于x轴的对称点C,连接AB、AC.若△ABC是直角三角形,则点A的坐标为 .
三、解答题
17.根据下列条件,分别求出二次函数的解析式.
(1)已知图象的顶点坐标为(﹣1,﹣8),且过点(0,﹣6);
(2)已知图象经过点A(﹣1,0)、B(0,3),且对称轴为直线x=1.
18.已知抛物线.
(1)写出它的开口方向、对称轴和顶点坐标;
(2)当为何值时,函数取得最大值,请求出这个最大值.
19.如图,利用一面墙(墙长10米)用20米的篱笆国成一个矩形场地.设垂直于墙的一边为x米.矩形场地的面积为s平方米.
(1)求s与x的函数关系式,并求出x的取值范围;
(2)若矩形场地的面积最大,应该如何设计长与宽.
20.如图,二次函数的图象与y交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数的图象经过该二次函数图象上的点及点B.
(1)求二次函数与一次函数的表达式.
(2)根据图象,写出满足的x的取值范围.
21.果园有果树60棵,现准备多种一些果树提高果园产量.如果多种树,那么树之间的距离和每棵果树所受光照就会减少,每棵果树的平均产量随之降低.根据经验,增种10棵果树时,果园内的每棵果树平均产量为75kg.在确保每棵果树平均产量不低于40kg的前提下,设增种果树(且为整数)棵,该果园每棵果树平均产量为kg,它们之间的函数关系满足如图所示的图像.
(1)每增种1棵果树时,每棵果树平均产量减少______kg;
(2)求与之间的函数关系式,并直接写出自变量的取值范围;
(3)当增种果树多少棵时,果园的总产量(kg)最大?最大产量是多少?
22.如图,已知抛物线经过A(-1,0),B(3,0)两点.
(1)求抛物线的解析式;
(2)当0
23.如图1是一座抛物线型拱桥侧面示意图.水面宽AB与桥长CD均为24m,在距离D点6米的E处,测得桥面到桥拱的距离EF为1.5m,以桥拱顶点O为原点,桥面为x轴建立平面直角坐标系.
(1)求桥拱项部O离水面的距离.
(2)如图2,桥面上方有3根高度均为4m的支柱CG,OH,DI,过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面距离为1m.
①求出其中一条钢缆抛物线的函数表达式.
②为庆祝节日,在钢缆和桥拱之间竖直装饰若干条彩带,求彩带长度的最小值.
24.如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,﹣1),且与y轴交于点C(0,3),与x轴交于A、B两点(点A在点B的右侧),点P是抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点 D.
(1)求该抛物线的函数关系式及A、B两点的坐标;
(2)求点P在运动的过程中,线段PD的最大值;
(3)若点P与点Q重合,点E在x轴上,点F在抛物线上,问是否存在以A,P,E,F为顶点的平行四边形?若存在,直接写出点F的坐标;若不存在,请说明理由.
同课章节目录
