2.3二次函数与一元二次方程、不等式(第2课时) 课件(共15张PPT)
文档属性
| 名称 | 2.3二次函数与一元二次方程、不等式(第2课时) 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 754.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-12 11:26:21 | ||
图片预览





文档简介
(共15张PPT)
2.3 二次函数与一元二次方程、不等式
(第二课时)
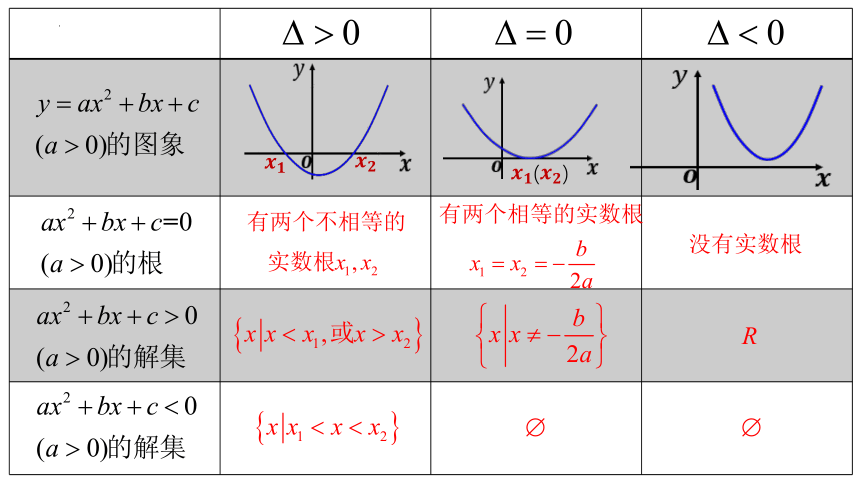
解一元二次不等式的步骤:
①化正:化为ax2+bx+c>0(a>0)
③求根:求方程ax2+bx+c=0的根
④画图:画函数y=ax2+bx+c(a>0)
的图象
因式分解or求根公式
大于取两边,小于取中间.
②判别:判别△确定有无实数根
⑤写解:由图象写出不等式的解集
()
分式不等式:分母中含有未知数的不等式叫分式不等式。
各种分式不等式经过同解变形,可以化为标准形式:
题型一:解分式不等式
例题:解不等式
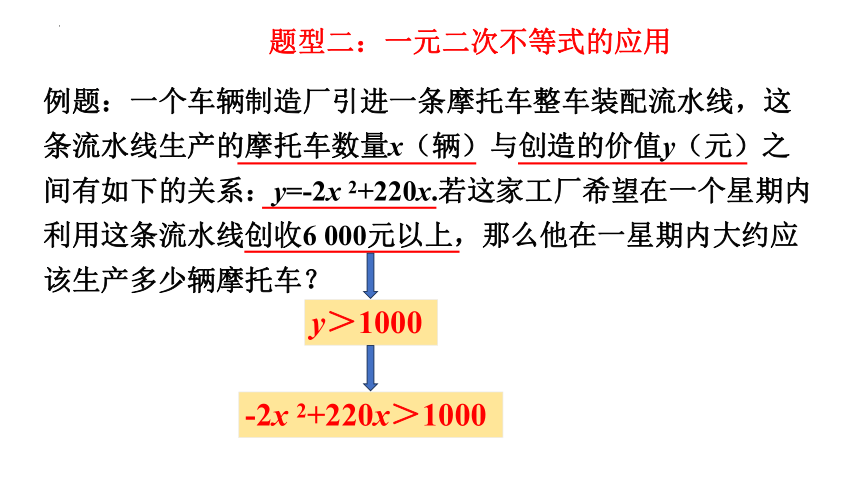
例题:一个车辆制造厂引进一条摩托车整车装配流水线,这条流水线生产的摩托车数量x(辆)与创造的价值y(元)之间有如下的关系:y=-2x 2+220x.若这家工厂希望在一个星期内利用这条流水线创收6 000元以上,那么他在一星期内大约应该生产多少辆摩托车?
题型二:一元二次不等式的应用
y>1000
-2x 2+220x>1000
解:设在一星期内大约应该生产x辆摩托车.
根据题意,得-2x2+220x>6 000.
整理得x2-110x+3 000<0.
对于方程x2-110x+3 000=0,Δ=100>0,
所以有两个实数根x1=50,x2=60,
画出二次函数y=x2-110x+3 000,
由图象得不等式的解集为{x|50<x<60}.
因为x只能取整数值,所以当这条摩托车整车装配流水线在一周内生产的摩托车数量在51到59辆之间时,这家工厂能够获得6 000元以上的收益.
变式:某种汽车在水泥路面上的刹车距离s(m)和汽车刹车前的车速v(km/h)之间有如下的关系: .在一次交通事故中,测得这种车的刹车距离大于39.5m,那么这辆汽车刹车前的速度至少是多少(精确到1km/h) ?
s >39.5
> 39.5
解:根据题意,得:
移项整理,得:
对于方程,,
方程有两个实数根,.
画出二次函数的图象,
结合图象得不等式的解集为或,
从而不等式的解集为或.
因为车速所以.
而所以这辆汽车刹车前的车速至少为
题型三:解简单的高次不等式
奇过偶不过
穿针引线法解高次不等式的具体步骤:
1.将不等式化为标准形式:一端为0,另一端为若干个一次因式(因式中的x的系数为正)或二次不可约因式的积.
2.求出各因式的实数根,并在数轴上依次标出.
3.自最右端上方起,用曲线自右向左依次由各根穿过数轴,遇奇次方根一次穿过,遇偶次方根穿而不过(奇过偶不过).
4.记数轴上方为正、下方为负,根据不等式的符号写出解集.
练习:
例.已知关于x的不等式kx2-6kx+k+8≥0对任意x∈R恒成立,求k的取值范围.
解:①当k=0时,不等式为8≥0恒成立,符合题意;
②当k>0时,不等式kx2-6kx+k+8≥0对任意x∈R恒成立,
则△=36k2-4k(k+8)≤0,解得0<k≤1;
③当k<0时,不等式kx2-6kx+k+8≥0不能对任意x∈R恒成立.
综上所述,k的取值范围是{k|0≤k≤1}.
题型四:含参数不等式
变式:对任意实数x,不等式(a-3)x2-2(a-3)x-6<0恒成立,求实数a的取值范围.
解:①当a-3=0,即a=3时,不等式为:-6<0,恒成立,则a=3满足题意.
②当a-3≠0,即a≠3时,不等式恒成立则需:,
解得:.
综上所述:.
2.3 二次函数与一元二次方程、不等式
(第二课时)
解一元二次不等式的步骤:
①化正:化为ax2+bx+c>0(a>0)
③求根:求方程ax2+bx+c=0的根
④画图:画函数y=ax2+bx+c(a>0)
的图象
因式分解or求根公式
大于取两边,小于取中间.
②判别:判别△确定有无实数根
⑤写解:由图象写出不等式的解集
()
分式不等式:分母中含有未知数的不等式叫分式不等式。
各种分式不等式经过同解变形,可以化为标准形式:
题型一:解分式不等式
例题:解不等式
例题:一个车辆制造厂引进一条摩托车整车装配流水线,这条流水线生产的摩托车数量x(辆)与创造的价值y(元)之间有如下的关系:y=-2x 2+220x.若这家工厂希望在一个星期内利用这条流水线创收6 000元以上,那么他在一星期内大约应该生产多少辆摩托车?
题型二:一元二次不等式的应用
y>1000
-2x 2+220x>1000
解:设在一星期内大约应该生产x辆摩托车.
根据题意,得-2x2+220x>6 000.
整理得x2-110x+3 000<0.
对于方程x2-110x+3 000=0,Δ=100>0,
所以有两个实数根x1=50,x2=60,
画出二次函数y=x2-110x+3 000,
由图象得不等式的解集为{x|50<x<60}.
因为x只能取整数值,所以当这条摩托车整车装配流水线在一周内生产的摩托车数量在51到59辆之间时,这家工厂能够获得6 000元以上的收益.
变式:某种汽车在水泥路面上的刹车距离s(m)和汽车刹车前的车速v(km/h)之间有如下的关系: .在一次交通事故中,测得这种车的刹车距离大于39.5m,那么这辆汽车刹车前的速度至少是多少(精确到1km/h) ?
s >39.5
> 39.5
解:根据题意,得:
移项整理,得:
对于方程,,
方程有两个实数根,.
画出二次函数的图象,
结合图象得不等式的解集为或,
从而不等式的解集为或.
因为车速所以.
而所以这辆汽车刹车前的车速至少为
题型三:解简单的高次不等式
奇过偶不过
穿针引线法解高次不等式的具体步骤:
1.将不等式化为标准形式:一端为0,另一端为若干个一次因式(因式中的x的系数为正)或二次不可约因式的积.
2.求出各因式的实数根,并在数轴上依次标出.
3.自最右端上方起,用曲线自右向左依次由各根穿过数轴,遇奇次方根一次穿过,遇偶次方根穿而不过(奇过偶不过).
4.记数轴上方为正、下方为负,根据不等式的符号写出解集.
练习:
例.已知关于x的不等式kx2-6kx+k+8≥0对任意x∈R恒成立,求k的取值范围.
解:①当k=0时,不等式为8≥0恒成立,符合题意;
②当k>0时,不等式kx2-6kx+k+8≥0对任意x∈R恒成立,
则△=36k2-4k(k+8)≤0,解得0<k≤1;
③当k<0时,不等式kx2-6kx+k+8≥0不能对任意x∈R恒成立.
综上所述,k的取值范围是{k|0≤k≤1}.
题型四:含参数不等式
变式:对任意实数x,不等式(a-3)x2-2(a-3)x-6<0恒成立,求实数a的取值范围.
解:①当a-3=0,即a=3时,不等式为:-6<0,恒成立,则a=3满足题意.
②当a-3≠0,即a≠3时,不等式恒成立则需:,
解得:.
综上所述:.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
