2.4.2圆的一般方程说课 课件(共35张PPT)
文档属性
| 名称 | 2.4.2圆的一般方程说课 课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-12 00:00:00 | ||
图片预览










文档简介
(共35张PPT)
第二章 直线和圆的方程
2.4.2 圆的一般方程
02
教学问题诊断分析
03
教学目标及其解析
04
教学活动过程设计
教学内容及其解析
01
目录
CONTENT
The analysis of teaching material
The analysis of learning condition
Teaching objectives
Teaching procedures
PART 01
教学内容及其解析
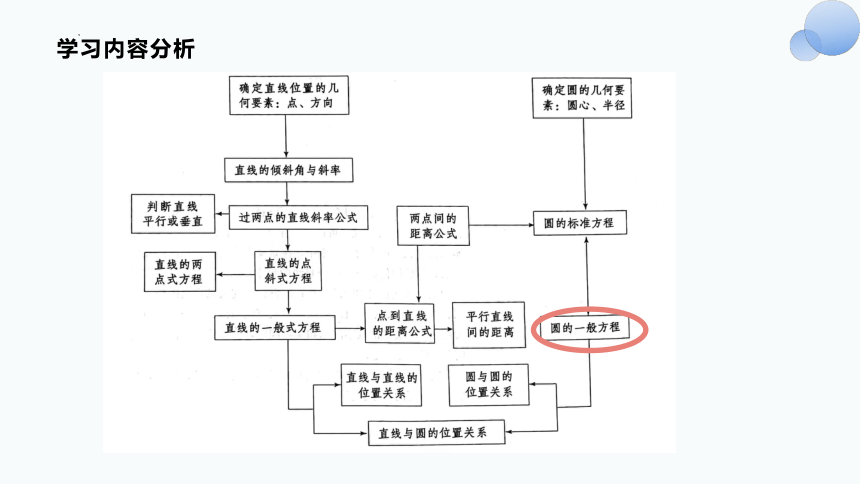
学习内容分析
课标分析:
《圆的一般方程》主要内容是圆的一般方程的定义、代数特征、求圆的一般方程以及与圆有关的简单的轨迹方程问题。
几何问题
代数问题
代数语言
学习内容分析
课程标准:
①回顾确定圆的几何要素,在平面直角坐标系中,探索并掌握圆的一般方程。
②能用直线和圆的方程解决一些简单的数学问题与实际问题。
学业要求:
能够根据几何问题和图形的特点,用代数语言把几何问题转化成为代数问题;根据对几何问题(图形) 的分析,探索解决问题的思路;运用代数方法得到结论;给出代数结论合理的几何解释,解决几何问题。
重点提升学生的数学运算、逻辑推理和数学抽象素养。
学习内容分析
学习内容分析
本节课内容分析:
本节课选自《2019人教A版高中数学选择性必修第一册》第二章《直线和圆的方程》,本节课主要学习圆的一般方程。本节内容是在学生学习了圆的标准方程基础上,进一步研究圆的一般方程,发现圆的方程特点,即为特殊的二元二次方程.以“圆”为载体,再次实践和感悟运用解析几何思想研究问题的一般思路.
同时,由于圆也是特殊的圆锥曲线,因此,学习了圆的方程,就为后面学习其它圆锥曲线的方程奠定了基础。也就是说,本节内容在教材体系中起到承上启下的作用,具有重要的地位。
同时,坐标法不仅是研究几何问题的重要方法,而且是一种广泛应用于其他领域的重要数学方法.通过坐标系,把点和坐标、曲线和方程联系起来,实现了形和数的统一.
PART 02
教学目标及其解析
学习目标解析
目标一:
理解圆的一般方程的概念.
达成目标的标志:
通过将圆的标准方程变形成一般方程,理解圆的一般方程与一般形式的二元二次方程之间的联系,能将圆的标准方程化为一般方程,培养数学抽象的核心素养.
学习目标解析
目标二:
掌握圆的一般方程的概念,能与标准方程互化,体会一般方程与标准方程的特点.
达成目标的标志:
通过对圆的一般方程和标准方程的互化,能正确理解圆的一般方程中系数所满足的条件,能判断任意一个二元二次方程是否是圆的一般方程,会由圆的一般方程求圆心和半径,发展数学运算的核心素养.
学习目标解析
目标三:
掌握圆的一般方程求解方法和与圆有关的简单的轨迹方程问题求解方法.
达成目标的标志:
通过具体例题的讲解,会用待定系数法求圆的一般方程以及用相关点法解决与圆有关的简单的轨迹方程问题,提升逻辑推理和直观想象的核心素养.
PART 03
教学问题诊断分析
教学问题诊断分析
难点1:
探究是否任意一个二元二次方程都可以表示圆.
认知基础:
圆的一般方程的探究过程与直线的一般式方程探究过程相似,学生已经经历过直线的一般式方程的探究过程,所以能进行圆的一般方程的探究.
学生初中已经学过配方法解一元二次方程,对利用配方法解决问题有一定的基础.
与将要达到水平的差异:
在圆的一般方程转化为标准方程的过程会遇到困难,即配方法的使用.
解决办法:
通过尝试配方例子中的几个二元二次方程,从特殊到一般,归纳方法.
教学问题诊断分析
难点2:
坐标法解决轨迹问题
认知基础:
在直线部分的学习和圆的标准方程的学习过程都是将几何元素与代数表示对应起来,将图形上的点与方程的解与平面直角坐标系中的坐标对应起来.
与将要达到水平的差异:
将已知的几何信息转化成代数语言,并找到其中蕴含的相等关系是比较困难的.
解决办法:
借助几何画板作图,直观形象地观察轨迹问题,体会利用几何的眼光看问题,找到问题的本质,用代数的方法解决问题.通过例题,让学生感悟几何元素与代数表示的对应关系.
PART 04
教学活动过程设计
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
课后作业
课前小测:请利用圆的标准方程回答下列问题:
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
课后作业
圆的方程有什么特点?
观察上面两个圆的方程,它们有什么特点?
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
课后作业
都是二元二次方程
圆的方程有什么特点?
任何一个圆的方程都是二元二次方程
x2+y2+Dx+Ey+F=0
可以写成
表示的图形都是圆吗?
①x2和 y2的系数是1;②没有xy项.
追问:任意一个二元二次方程表示的图形都是圆吗?
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
课后作业
尝试判断
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
课后作业
当 满足什么条件时,方程表示圆呢?
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
课后作业
当D2+E2-4F > 0时,方程表示圆.
当D2+E2-4F = 0时,方程表示点.
当D2+E2-4F< 0时,方程不表示任何图形.
当 满足什么条件时,方程表示圆呢?
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
课后作业
圆的一般方程
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
课后作业
做一做
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
课后作业
例1
例题讲解
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
课后作业
设一般方程
设标准方程
例2 已知线段AB的端点B
的坐标是(4,3),端点A在
圆x2+y2+2x-3=0上运动,
求线段AB的中点M的轨迹方
程,并说明是什么图形.
例题讲解
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
相关点法
①若动点P(x,y)随着点Q(x1,y1)运动而运动,且知道点Q所在的曲线
②用x,y表示x1,y1
③将Q点的坐标代入已知的曲线方程,即得动点P的轨迹方程
例题讲解
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
做一做
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
做一做
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
圆的两种方程
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
应用圆的方程解决简单的数学问题
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
课后作业
A组
课后作业
A组
课后作业
B组
请大家批评指正
第二章 直线和圆的方程
2.4.2 圆的一般方程
02
教学问题诊断分析
03
教学目标及其解析
04
教学活动过程设计
教学内容及其解析
01
目录
CONTENT
The analysis of teaching material
The analysis of learning condition
Teaching objectives
Teaching procedures
PART 01
教学内容及其解析
学习内容分析
课标分析:
《圆的一般方程》主要内容是圆的一般方程的定义、代数特征、求圆的一般方程以及与圆有关的简单的轨迹方程问题。
几何问题
代数问题
代数语言
学习内容分析
课程标准:
①回顾确定圆的几何要素,在平面直角坐标系中,探索并掌握圆的一般方程。
②能用直线和圆的方程解决一些简单的数学问题与实际问题。
学业要求:
能够根据几何问题和图形的特点,用代数语言把几何问题转化成为代数问题;根据对几何问题(图形) 的分析,探索解决问题的思路;运用代数方法得到结论;给出代数结论合理的几何解释,解决几何问题。
重点提升学生的数学运算、逻辑推理和数学抽象素养。
学习内容分析
学习内容分析
本节课内容分析:
本节课选自《2019人教A版高中数学选择性必修第一册》第二章《直线和圆的方程》,本节课主要学习圆的一般方程。本节内容是在学生学习了圆的标准方程基础上,进一步研究圆的一般方程,发现圆的方程特点,即为特殊的二元二次方程.以“圆”为载体,再次实践和感悟运用解析几何思想研究问题的一般思路.
同时,由于圆也是特殊的圆锥曲线,因此,学习了圆的方程,就为后面学习其它圆锥曲线的方程奠定了基础。也就是说,本节内容在教材体系中起到承上启下的作用,具有重要的地位。
同时,坐标法不仅是研究几何问题的重要方法,而且是一种广泛应用于其他领域的重要数学方法.通过坐标系,把点和坐标、曲线和方程联系起来,实现了形和数的统一.
PART 02
教学目标及其解析
学习目标解析
目标一:
理解圆的一般方程的概念.
达成目标的标志:
通过将圆的标准方程变形成一般方程,理解圆的一般方程与一般形式的二元二次方程之间的联系,能将圆的标准方程化为一般方程,培养数学抽象的核心素养.
学习目标解析
目标二:
掌握圆的一般方程的概念,能与标准方程互化,体会一般方程与标准方程的特点.
达成目标的标志:
通过对圆的一般方程和标准方程的互化,能正确理解圆的一般方程中系数所满足的条件,能判断任意一个二元二次方程是否是圆的一般方程,会由圆的一般方程求圆心和半径,发展数学运算的核心素养.
学习目标解析
目标三:
掌握圆的一般方程求解方法和与圆有关的简单的轨迹方程问题求解方法.
达成目标的标志:
通过具体例题的讲解,会用待定系数法求圆的一般方程以及用相关点法解决与圆有关的简单的轨迹方程问题,提升逻辑推理和直观想象的核心素养.
PART 03
教学问题诊断分析
教学问题诊断分析
难点1:
探究是否任意一个二元二次方程都可以表示圆.
认知基础:
圆的一般方程的探究过程与直线的一般式方程探究过程相似,学生已经经历过直线的一般式方程的探究过程,所以能进行圆的一般方程的探究.
学生初中已经学过配方法解一元二次方程,对利用配方法解决问题有一定的基础.
与将要达到水平的差异:
在圆的一般方程转化为标准方程的过程会遇到困难,即配方法的使用.
解决办法:
通过尝试配方例子中的几个二元二次方程,从特殊到一般,归纳方法.
教学问题诊断分析
难点2:
坐标法解决轨迹问题
认知基础:
在直线部分的学习和圆的标准方程的学习过程都是将几何元素与代数表示对应起来,将图形上的点与方程的解与平面直角坐标系中的坐标对应起来.
与将要达到水平的差异:
将已知的几何信息转化成代数语言,并找到其中蕴含的相等关系是比较困难的.
解决办法:
借助几何画板作图,直观形象地观察轨迹问题,体会利用几何的眼光看问题,找到问题的本质,用代数的方法解决问题.通过例题,让学生感悟几何元素与代数表示的对应关系.
PART 04
教学活动过程设计
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
课后作业
课前小测:请利用圆的标准方程回答下列问题:
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
课后作业
圆的方程有什么特点?
观察上面两个圆的方程,它们有什么特点?
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
课后作业
都是二元二次方程
圆的方程有什么特点?
任何一个圆的方程都是二元二次方程
x2+y2+Dx+Ey+F=0
可以写成
表示的图形都是圆吗?
①x2和 y2的系数是1;②没有xy项.
追问:任意一个二元二次方程表示的图形都是圆吗?
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
课后作业
尝试判断
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
课后作业
当 满足什么条件时,方程表示圆呢?
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
课后作业
当D2+E2-4F > 0时,方程表示圆.
当D2+E2-4F = 0时,方程表示点.
当D2+E2-4F< 0时,方程不表示任何图形.
当 满足什么条件时,方程表示圆呢?
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
课后作业
圆的一般方程
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
课后作业
做一做
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
课后作业
例1
例题讲解
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
课后作业
设一般方程
设标准方程
例2 已知线段AB的端点B
的坐标是(4,3),端点A在
圆x2+y2+2x-3=0上运动,
求线段AB的中点M的轨迹方
程,并说明是什么图形.
例题讲解
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
相关点法
①若动点P(x,y)随着点Q(x1,y1)运动而运动,且知道点Q所在的曲线
②用x,y表示x1,y1
③将Q点的坐标代入已知的曲线方程,即得动点P的轨迹方程
例题讲解
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
做一做
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
做一做
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
圆的两种方程
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
应用圆的方程解决简单的数学问题
知识准备
概念的形成
概念的理解
概念的应用
课堂练习
反思与小结
课后作业
A组
课后作业
A组
课后作业
B组
请大家批评指正
