第二章 直线与圆的方程 课说课 课件(共24张PPT)
文档属性
| 名称 | 第二章 直线与圆的方程 课说课 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-12 11:29:44 | ||
图片预览








文档简介
(共24张PPT)
第二章 平面解析几何
【学习内容分析】
本节课是直线与圆部分的习题课,学生已经学习了直线与圆的方程、点到直线的距离公式、直线与圆的位置关系等内容,因此本节课是对已学内容的巩固深化和拓展延伸;通过求动点的轨迹,使学生进一步体会坐标法在解析几何中的应用,后面学习圆锥曲线等内容奠定基础.
蕴含的数学思想和方法:
直线与圆是解析几何的起始内容,解析几何是以数形结合思想贯穿始终,以坐标法统领全局.通过这一部分内容的学习,学生初步体会解析几何的基本思想方法,用代数方法解决几何问题.
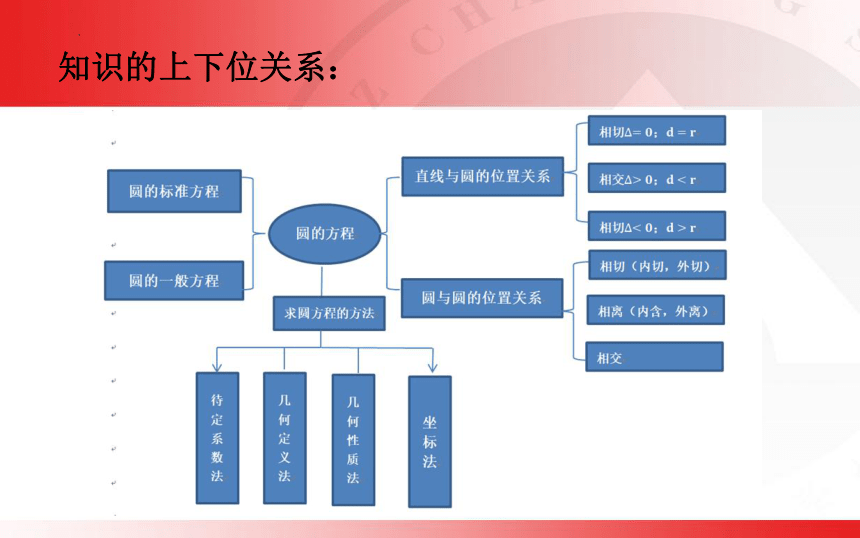
知识的上下位关系:
1. 知识技能储备:学生前面学习了直线和圆的方程,并学习了判断直线与圆的位置关系的两种方法,学生初步掌握了如何将几何问题转化为代数问题,并利用代数运算研究几何性质,对解析几何解决问题的基本思想方法有了一定的认识.
2.学习中困难:对于与圆相关的动点轨迹问题一直是个难点,尤其是学生对坐标法的应用还存在一定困难,几何条件怎样合理的代数化以及代数化后的化简和分类讨论,还需要老师给与相应的指导.
【学情分析】
【教学目标】
1.通过引入问题,引导学生思考圆上的点所满足的几何条件.培养学生的直观想象素养.
2.通过求动点轨迹方程,使学生经历坐标法的完整过程,培养学生数学运算和逻辑推理等核心素养.
3.通过对含参数方程的分类讨论,使学生经历由特殊到一般的过程,培养分类讨论的思想.
(一)提出问题,引发思考
(一)提出问题,引发思考
(二)深究问题,典例分析
(二)深究问题,典例分析
(二)深究问题,典例分析
设计意图:例2的第1问是阿波罗尼斯圆的一种特殊情况,目的让学生经历坐标法求轨迹方程的过程,体会坐标法的作用和步骤,同时也为后面证明一般情况做铺垫.
(二)问题深入,典例分析
(三)特殊到一般,推广延伸
设计意图:体会研究数学问题的一般过程,
由特殊到一般,先大胆猜想再严谨证明。
【用ggb软件操作确认】
(四)梳理问题,形成策略
1.坐标法:建系设点——列方程(几何条件用坐标表示)——化简——检验完备性.
2.求轨迹圆:
(五)反思与小结
第二章 平面解析几何
【学习内容分析】
本节课是直线与圆部分的习题课,学生已经学习了直线与圆的方程、点到直线的距离公式、直线与圆的位置关系等内容,因此本节课是对已学内容的巩固深化和拓展延伸;通过求动点的轨迹,使学生进一步体会坐标法在解析几何中的应用,后面学习圆锥曲线等内容奠定基础.
蕴含的数学思想和方法:
直线与圆是解析几何的起始内容,解析几何是以数形结合思想贯穿始终,以坐标法统领全局.通过这一部分内容的学习,学生初步体会解析几何的基本思想方法,用代数方法解决几何问题.
知识的上下位关系:
1. 知识技能储备:学生前面学习了直线和圆的方程,并学习了判断直线与圆的位置关系的两种方法,学生初步掌握了如何将几何问题转化为代数问题,并利用代数运算研究几何性质,对解析几何解决问题的基本思想方法有了一定的认识.
2.学习中困难:对于与圆相关的动点轨迹问题一直是个难点,尤其是学生对坐标法的应用还存在一定困难,几何条件怎样合理的代数化以及代数化后的化简和分类讨论,还需要老师给与相应的指导.
【学情分析】
【教学目标】
1.通过引入问题,引导学生思考圆上的点所满足的几何条件.培养学生的直观想象素养.
2.通过求动点轨迹方程,使学生经历坐标法的完整过程,培养学生数学运算和逻辑推理等核心素养.
3.通过对含参数方程的分类讨论,使学生经历由特殊到一般的过程,培养分类讨论的思想.
(一)提出问题,引发思考
(一)提出问题,引发思考
(二)深究问题,典例分析
(二)深究问题,典例分析
(二)深究问题,典例分析
设计意图:例2的第1问是阿波罗尼斯圆的一种特殊情况,目的让学生经历坐标法求轨迹方程的过程,体会坐标法的作用和步骤,同时也为后面证明一般情况做铺垫.
(二)问题深入,典例分析
(三)特殊到一般,推广延伸
设计意图:体会研究数学问题的一般过程,
由特殊到一般,先大胆猜想再严谨证明。
【用ggb软件操作确认】
(四)梳理问题,形成策略
1.坐标法:建系设点——列方程(几何条件用坐标表示)——化简——检验完备性.
2.求轨迹圆:
(五)反思与小结
