2.1直线的倾斜角与斜率 说课课件(共33张PPT)
文档属性
| 名称 | 2.1直线的倾斜角与斜率 说课课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-12 11:33:12 | ||
图片预览







文档简介
(共33张PPT)
2.1 直线的倾斜角与斜率
01
02
03
04
05
说课过程
平面解析几何
教学内容
教学目标
学生学情
教学策略
教学过程
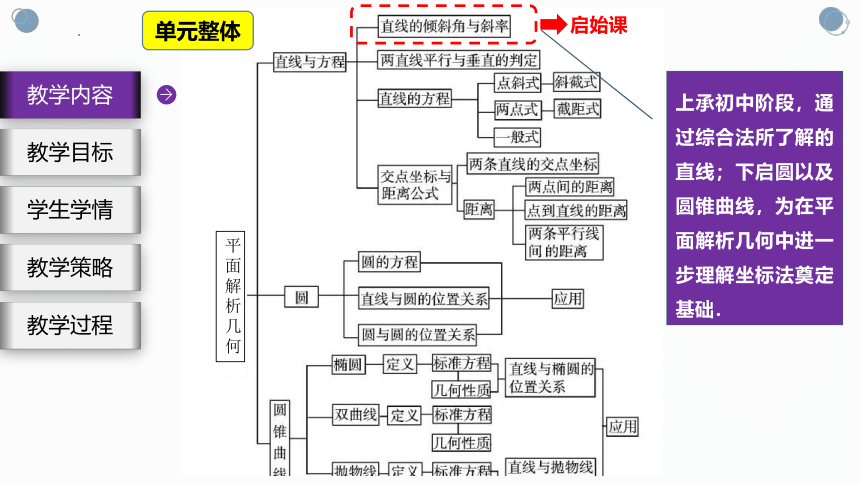
上承初中阶段,通过综合法所了解的直线;下启圆以及圆锥曲线,为在平面解析几何中进一步理解坐标法奠定基础.
启始课
单元整体
教学内容
教学目标
学生学情
教学策略
教学过程
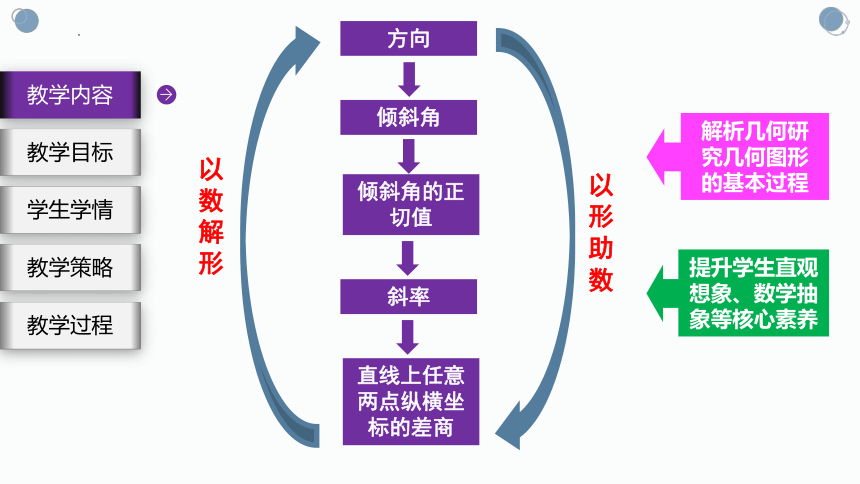
以形助数
方向
倾斜角
倾斜角的正切值
斜率
直线上任意两点纵横坐标的差商
以数解形
解析几何研
究几何图形
的基本过程
提升学生直观想象、数学抽象等核心素养
教学目标
教学内容
学生学情
教学策略
教学过程
一
通过微课,了解解析几何的发展史和坐标法的思想,把握整章的研究内容和方法.
二
通过课件动态演示,理解直线倾斜角、斜率概念定义的合理性,发展直观想象素养.
三
经历从特殊到一般刻画直线斜率的过程,掌握过两点的直线的斜率公式,发展数学抽象素养
学生学情
教学内容
教学目标
教学策略
教学过程
已有的知识经验
学生在初中阶段学面直角坐标系的相关概念,知道了直角坐标系中点与有序实数对之间的一一对应关系,并且掌握了两点确定一条直线等直线有关知识。高中阶段借助平面直角坐标系和单位圆研究了三角函数,掌握了正切函数的图像和性质,具备了一定的的知识基础以及数形结合的思想。在平面向量和空间向量的学习中,学生也掌握了沟通几何和代数的工具——向量,获得平面直角坐标系是沟通代数和几何的桥梁的经验,会用向量法解决几何问题。
学生学情
教学内容
教学目标
教学策略
教学过程
可能存在的障碍点 1.虽然学生对直角坐标系非常熟悉,但如何利用直角坐标系刻画直线的方向这个要素,是与平面几何有质的不同的地方,也是学生所不习惯的。
2.斜率概念的引入是以一个点和一个方向、两个点都能唯一确定一条直线,那么它们一定有内在联系为指导思想,在已知两个点的坐标时,探究如何用坐标表示倾斜角,这一过程虽然十分简洁,但对学生的抽象思维要求很高。
3.在推导过两点的直线斜率公式时,需要联系向量、三角函数等相关知识还要进行分类讨论,需要充分调动以往的知识经验,对于学生来说难度较大。而且斜率与方向向量的坐标表示具有内在一致性学生也不容易想到。
学生学情
教学内容
教学目标
教学策略
教学过程
重点:直线的倾斜角与斜率的概念、过两点的斜率公式
难点:直线倾斜角的抽象、斜率公式的推导
教学内容
教学目标
教学策略
教学过程
学生学情
教学过程
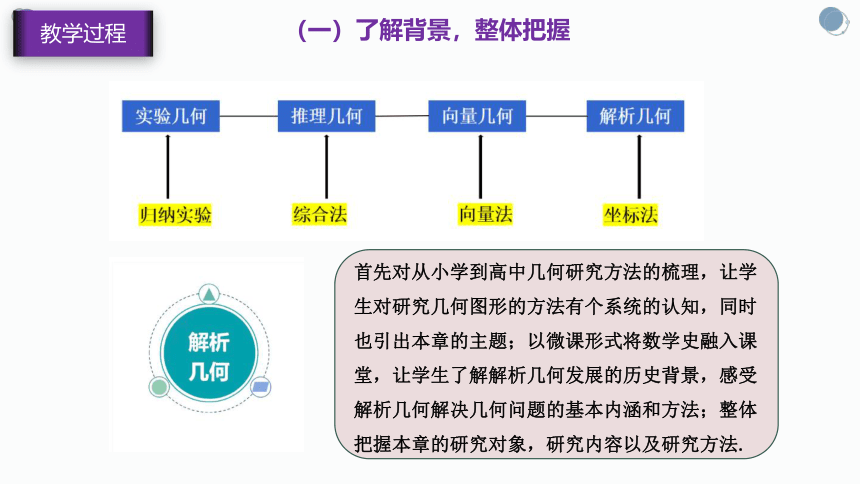
(一)了解背景,整体把握
首先对从小学到高中几何研究方法的梳理,让学生对研究几何图形的方法有个系统的认知,同时也引出本章的主题;以微课形式将数学史融入课堂,让学生了解解析几何发展的历史背景,感受解析几何解决几何问题的基本内涵和方法;整体把握本章的研究对象,研究内容以及研究方法.
教学过程
(二)复习回顾,引入新知
【问题1】确定一条直线的几何要素有哪些?
①两个点
②一个点和一个方向
教学过程
(二)复习回顾,引入新知
【问题1】确定一条直线的几何要素有哪些?
①两个点
②一个点和一个方向
教学过程
【问题1】确定一条直线的几何要素有哪些?
【问题2】如何刻画这些直线的方向?
(三)合作交流,探究新知
教学过程
【问题1】确定一条直线的几何要素有哪些?
【问题2】如何刻画这些直线的方向?
【追问2】观察直线绕点 P 变化的过程,思考可以用
哪个量刻画直线的方向?
【追问1】在平面直角坐标系中,过定点P可作出无数
条直线,对比这些直线它们的区别是什么?
(三)合作交流,探究新知
教学过程
【问题1】
【问题2】
【追问2】
【追问1】
追问2借助信息技术演示直线绕点P变化的过程,使学生能更加清晰地感受随着倾斜程度的不同直线向上的方向与x轴正方向的夹角也随之不同.
通过追问1强调以直角坐标系为参照系,探究区分不同位置直线的方法,引导学生感受直角坐标系中利用倾斜角刻画直线方向的合理性.
(三)合作交流,探究新知
教学过程
【问题1】
【问题2】
【追问2】
【追问1】
追问2借助信息技术演示直线绕点P变化的过程,使学生能更加清晰地感受随着倾斜程度的不同直线向上的方向与x轴正方向的夹角也随之不同. 最后,借助追问3,引导学生自主归纳,教师补充,从而抽象出倾斜角的概念.
通过强调以直角坐标系为参照系,探究区分不同位置直线的方法,引导学生感受直角坐标系中利用倾斜角刻画直线方向的合理性.
【追问3】在直角坐标系中可以以哪个轴为基准,定义一个角刻画直线的方向呢?
(三)合作交流,探究新知
教学过程
(三)合作交流,探究新知
【倾斜角的定义】当直线 与 轴相交时,我们以 轴为基准,轴正向与直线 向上的方向之间所成的角α叫做直线 的倾斜角.
教学过程
(三)合作交流,探究新知
【倾斜角的定义】当直线 与 轴相交时,我们以 轴为基准,轴正向与直线 向上的方向之间所成的角α叫做直线 的倾斜角.
【追问1】倾斜角的定义是否适用于所有直线?
【追问2】依据定义,倾斜角的取值范围是什么
研究数学对象时,往往要通过探索特例或进行推广,从而对问题有更深入的认识。给出倾斜角定义后,通过追问1,一方面给出特殊直线倾斜角的规定,另一方面为追问2中倾斜角的范围研究做铺垫,提升思维的严谨性。
教学过程
(三)合作交流,探究新知
【倾斜角的定义】当直线 与 轴相交时,我们以 轴为基准,轴正向与直线 向上的方向之间所成的角α叫做直线 的倾斜角.
在平面直角坐标系中,每一条直线都有一个确定的倾斜角,而且方向相同的直线,其倾斜程度相同,倾斜角相等;方向不同的直线,其倾斜程度不同,倾斜角也不相等.因此,我们可以用倾斜角表示平面直角坐标系中一条直线的倾斜程度,也就表示了直线的方向.
教学过程
(四)代数量化,探寻结论
【问题3】设P1(x1,y1),P2(x2,y2) (其中 ) 是直线 l 上的两点,由两点确定一条直线可知,直线 l 由点P1、P2唯一确定.所以,可以推断直线的倾斜角与P1、P2的坐标有内在联系.具有怎样的联系呢
教学过程
(四)代数量化,探寻结论
【问题3】设P1(x1,y1),P2(x2,y2) (其中 ) 是直线 l 上的两点,由两点确定一条直线可知,直线 l 由点P1、P2唯一确定.所以,可以推断直线的倾斜角与P1、P2的坐标有内在联系.具有怎样的联系呢
【探究】在平面直角坐标系中,设直线 l 的倾斜角为 .
教学过程
(四)代数量化,探寻结论
【探究】在平面直角坐标系中,设直线 l 的倾斜角为 .
师生活动:探究1由学生自主做答,教师引导学生回顾正切函数的定义,可以不刻意引导采用向量法;探究2采用学生展示交流的方式,鼓励用不同方法解决但以向量方法为重点,这个过程中教师可根据学情适当引导,如类比问题1想用正切函数的定义需要怎么做,从而启发学生想到平移,再结合向量在平移前后大小和方向保持不变的性质,引导学生借助向量去解决等;
教学过程
(四)代数量化,探寻结论
【探究】在平面直角坐标系中,设直线 l 的倾斜角为 .
师生活动:在前两个问题的基础上,问题3采用小组合作的方式,得出一般结论,在这个过程中,根据学情教师可以提示“一般情况如何画出图形?需要怎样分类?”并追问“当直线与 x 轴平行或重合时,上述式子还成立吗?为什么?”得出结论:画图不必考虑点P所在的坐标位置,只需要考虑两点的相对位置。
教学过程
(四)代数量化,探寻结论
【问题3】
【探究】
小组合作
特殊到一般
通过小组合作、交流、质疑补充,在思维碰撞的过程中逐步完善倾斜角正切值与两点坐标的关系,感受和总结出公式的适应范围以及与两点的顺序无关等结论。这一过程中,体现了数学从特殊到一般的研究方法,逐步将几何问题代数化,培养学生直观想象、逻辑推理核心素养。
教学过程
(四)代数量化,探寻结论
【问题3】
【探究】
【问题4】从上面的探究可以得出什么结论?
教学过程
(四)代数量化,探寻结论
【问题3】
【探究】
【问题4】
教学过程
(四)代数量化,探寻结论
【问题3】
【探究】
【问题4】
【追问1】可以用斜率表示直线的倾斜程度吗?
【追问2】倾斜角和斜率都是描述直线倾斜程度,
它们的差异和联系是什么?
【追问3】生活中有类似斜率的量吗?
【追问4】当直线的倾斜角由逐渐增大到时,
其斜率取值范围是什么?是如何变化的?
通过上述思考加深学生对直线斜率的理解,体会倾斜角与斜率的对应关系,理解斜率可以用来刻画倾斜角的合理性,增强思维的严谨性.
教学过程
(四)代数量化,探寻结论
【问题5】已知直线 经过两点,且直线斜率为 ,你能
发现直线的方向向量(1,k)与斜率之间的关系吗
问题5的设计是为了探究斜率与方向向量的关系,是直线方向的表示要素间关系的进一步总结,体现数学内部的知识联系,使得知识的呈现更具有逻辑性和整体性。考虑到本节的重点是倾斜角与斜率的探究,因此这里的探究以具体问题的形式呈现,一方面是为了给学生的探究提供方向性,另一方面是作为斜率的简单应用。
教学过程
(五)初步应用,巩固新知
【例1】如图,已知求直线的斜率,并判断这些
直线的倾斜角是锐角还是钝角.
【例2】如图为斜拉的钢丝锁抽象出来的部分直线,比较它们的倾斜角以及斜率的大小 .
教学过程
(五)初步应用,巩固新知
【例1】如图,已知求直线的斜率,并判断这些
直线的倾斜角是锐角还是钝角.
【例2】如图为斜拉的钢丝锁抽象出来的部分直线,比较它们的倾斜角以及斜率的大小 .
例1一方面考察了斜率公式的掌握,另一方面考察了斜率与倾斜角的联系,也是一个从形到数再到形的过程,让学生知道不仅要会用代数语言表示几何特征,还要会把代数运算得出的结果翻译成几何结论,体现了坐标法中把几何问题代数化,再通过代数运算研究几何性质的思想。
教学过程
(五)初步应用,巩固新知
【例1】如图,已知求直线的斜率,并判断这些
直线的倾斜角是锐角还是钝角.
【例2】如图为斜拉的钢丝锁抽象出来的部分直线,比较它们的倾斜角以及斜率的大小 .
例1一方面考察了斜率公式的掌握,另一方面考察了斜率与倾斜角的联系,也是一个从形到数再到形的过程,让学生知道不仅要会用代数语言表示几何特征,还要会把代数运算得出的结果翻译成几何结论,体现了坐标法中把几何问题代数化,再通过代数运算研究几何性质的思想。
通过对斜拉索所在直线倾斜角和斜率的大小比较,一方面加深倾斜角概念的理解,另一方面考察随着倾斜角的变化斜率变化的趋势。
教学过程
(六)学有所思,形成结构
【问题6】我们的研究思路是什么?用到了什么数学思想方法?
问题6是对本节课的研究框架进行的梳理,在这个梳理的过程中,一方面让学生重现研究过程,初步体会坐标法的研究思路,另一方面结合具体研究内容渗透相关的数学思想方法,如数形结合、从特殊到一般、转化化归等等。
感谢观看
2.1 直线的倾斜角与斜率
01
02
03
04
05
说课过程
平面解析几何
教学内容
教学目标
学生学情
教学策略
教学过程
上承初中阶段,通过综合法所了解的直线;下启圆以及圆锥曲线,为在平面解析几何中进一步理解坐标法奠定基础.
启始课
单元整体
教学内容
教学目标
学生学情
教学策略
教学过程
以形助数
方向
倾斜角
倾斜角的正切值
斜率
直线上任意两点纵横坐标的差商
以数解形
解析几何研
究几何图形
的基本过程
提升学生直观想象、数学抽象等核心素养
教学目标
教学内容
学生学情
教学策略
教学过程
一
通过微课,了解解析几何的发展史和坐标法的思想,把握整章的研究内容和方法.
二
通过课件动态演示,理解直线倾斜角、斜率概念定义的合理性,发展直观想象素养.
三
经历从特殊到一般刻画直线斜率的过程,掌握过两点的直线的斜率公式,发展数学抽象素养
学生学情
教学内容
教学目标
教学策略
教学过程
已有的知识经验
学生在初中阶段学面直角坐标系的相关概念,知道了直角坐标系中点与有序实数对之间的一一对应关系,并且掌握了两点确定一条直线等直线有关知识。高中阶段借助平面直角坐标系和单位圆研究了三角函数,掌握了正切函数的图像和性质,具备了一定的的知识基础以及数形结合的思想。在平面向量和空间向量的学习中,学生也掌握了沟通几何和代数的工具——向量,获得平面直角坐标系是沟通代数和几何的桥梁的经验,会用向量法解决几何问题。
学生学情
教学内容
教学目标
教学策略
教学过程
可能存在的障碍点 1.虽然学生对直角坐标系非常熟悉,但如何利用直角坐标系刻画直线的方向这个要素,是与平面几何有质的不同的地方,也是学生所不习惯的。
2.斜率概念的引入是以一个点和一个方向、两个点都能唯一确定一条直线,那么它们一定有内在联系为指导思想,在已知两个点的坐标时,探究如何用坐标表示倾斜角,这一过程虽然十分简洁,但对学生的抽象思维要求很高。
3.在推导过两点的直线斜率公式时,需要联系向量、三角函数等相关知识还要进行分类讨论,需要充分调动以往的知识经验,对于学生来说难度较大。而且斜率与方向向量的坐标表示具有内在一致性学生也不容易想到。
学生学情
教学内容
教学目标
教学策略
教学过程
重点:直线的倾斜角与斜率的概念、过两点的斜率公式
难点:直线倾斜角的抽象、斜率公式的推导
教学内容
教学目标
教学策略
教学过程
学生学情
教学过程
(一)了解背景,整体把握
首先对从小学到高中几何研究方法的梳理,让学生对研究几何图形的方法有个系统的认知,同时也引出本章的主题;以微课形式将数学史融入课堂,让学生了解解析几何发展的历史背景,感受解析几何解决几何问题的基本内涵和方法;整体把握本章的研究对象,研究内容以及研究方法.
教学过程
(二)复习回顾,引入新知
【问题1】确定一条直线的几何要素有哪些?
①两个点
②一个点和一个方向
教学过程
(二)复习回顾,引入新知
【问题1】确定一条直线的几何要素有哪些?
①两个点
②一个点和一个方向
教学过程
【问题1】确定一条直线的几何要素有哪些?
【问题2】如何刻画这些直线的方向?
(三)合作交流,探究新知
教学过程
【问题1】确定一条直线的几何要素有哪些?
【问题2】如何刻画这些直线的方向?
【追问2】观察直线绕点 P 变化的过程,思考可以用
哪个量刻画直线的方向?
【追问1】在平面直角坐标系中,过定点P可作出无数
条直线,对比这些直线它们的区别是什么?
(三)合作交流,探究新知
教学过程
【问题1】
【问题2】
【追问2】
【追问1】
追问2借助信息技术演示直线绕点P变化的过程,使学生能更加清晰地感受随着倾斜程度的不同直线向上的方向与x轴正方向的夹角也随之不同.
通过追问1强调以直角坐标系为参照系,探究区分不同位置直线的方法,引导学生感受直角坐标系中利用倾斜角刻画直线方向的合理性.
(三)合作交流,探究新知
教学过程
【问题1】
【问题2】
【追问2】
【追问1】
追问2借助信息技术演示直线绕点P变化的过程,使学生能更加清晰地感受随着倾斜程度的不同直线向上的方向与x轴正方向的夹角也随之不同. 最后,借助追问3,引导学生自主归纳,教师补充,从而抽象出倾斜角的概念.
通过强调以直角坐标系为参照系,探究区分不同位置直线的方法,引导学生感受直角坐标系中利用倾斜角刻画直线方向的合理性.
【追问3】在直角坐标系中可以以哪个轴为基准,定义一个角刻画直线的方向呢?
(三)合作交流,探究新知
教学过程
(三)合作交流,探究新知
【倾斜角的定义】当直线 与 轴相交时,我们以 轴为基准,轴正向与直线 向上的方向之间所成的角α叫做直线 的倾斜角.
教学过程
(三)合作交流,探究新知
【倾斜角的定义】当直线 与 轴相交时,我们以 轴为基准,轴正向与直线 向上的方向之间所成的角α叫做直线 的倾斜角.
【追问1】倾斜角的定义是否适用于所有直线?
【追问2】依据定义,倾斜角的取值范围是什么
研究数学对象时,往往要通过探索特例或进行推广,从而对问题有更深入的认识。给出倾斜角定义后,通过追问1,一方面给出特殊直线倾斜角的规定,另一方面为追问2中倾斜角的范围研究做铺垫,提升思维的严谨性。
教学过程
(三)合作交流,探究新知
【倾斜角的定义】当直线 与 轴相交时,我们以 轴为基准,轴正向与直线 向上的方向之间所成的角α叫做直线 的倾斜角.
在平面直角坐标系中,每一条直线都有一个确定的倾斜角,而且方向相同的直线,其倾斜程度相同,倾斜角相等;方向不同的直线,其倾斜程度不同,倾斜角也不相等.因此,我们可以用倾斜角表示平面直角坐标系中一条直线的倾斜程度,也就表示了直线的方向.
教学过程
(四)代数量化,探寻结论
【问题3】设P1(x1,y1),P2(x2,y2) (其中 ) 是直线 l 上的两点,由两点确定一条直线可知,直线 l 由点P1、P2唯一确定.所以,可以推断直线的倾斜角与P1、P2的坐标有内在联系.具有怎样的联系呢
教学过程
(四)代数量化,探寻结论
【问题3】设P1(x1,y1),P2(x2,y2) (其中 ) 是直线 l 上的两点,由两点确定一条直线可知,直线 l 由点P1、P2唯一确定.所以,可以推断直线的倾斜角与P1、P2的坐标有内在联系.具有怎样的联系呢
【探究】在平面直角坐标系中,设直线 l 的倾斜角为 .
教学过程
(四)代数量化,探寻结论
【探究】在平面直角坐标系中,设直线 l 的倾斜角为 .
师生活动:探究1由学生自主做答,教师引导学生回顾正切函数的定义,可以不刻意引导采用向量法;探究2采用学生展示交流的方式,鼓励用不同方法解决但以向量方法为重点,这个过程中教师可根据学情适当引导,如类比问题1想用正切函数的定义需要怎么做,从而启发学生想到平移,再结合向量在平移前后大小和方向保持不变的性质,引导学生借助向量去解决等;
教学过程
(四)代数量化,探寻结论
【探究】在平面直角坐标系中,设直线 l 的倾斜角为 .
师生活动:在前两个问题的基础上,问题3采用小组合作的方式,得出一般结论,在这个过程中,根据学情教师可以提示“一般情况如何画出图形?需要怎样分类?”并追问“当直线与 x 轴平行或重合时,上述式子还成立吗?为什么?”得出结论:画图不必考虑点P所在的坐标位置,只需要考虑两点的相对位置。
教学过程
(四)代数量化,探寻结论
【问题3】
【探究】
小组合作
特殊到一般
通过小组合作、交流、质疑补充,在思维碰撞的过程中逐步完善倾斜角正切值与两点坐标的关系,感受和总结出公式的适应范围以及与两点的顺序无关等结论。这一过程中,体现了数学从特殊到一般的研究方法,逐步将几何问题代数化,培养学生直观想象、逻辑推理核心素养。
教学过程
(四)代数量化,探寻结论
【问题3】
【探究】
【问题4】从上面的探究可以得出什么结论?
教学过程
(四)代数量化,探寻结论
【问题3】
【探究】
【问题4】
教学过程
(四)代数量化,探寻结论
【问题3】
【探究】
【问题4】
【追问1】可以用斜率表示直线的倾斜程度吗?
【追问2】倾斜角和斜率都是描述直线倾斜程度,
它们的差异和联系是什么?
【追问3】生活中有类似斜率的量吗?
【追问4】当直线的倾斜角由逐渐增大到时,
其斜率取值范围是什么?是如何变化的?
通过上述思考加深学生对直线斜率的理解,体会倾斜角与斜率的对应关系,理解斜率可以用来刻画倾斜角的合理性,增强思维的严谨性.
教学过程
(四)代数量化,探寻结论
【问题5】已知直线 经过两点,且直线斜率为 ,你能
发现直线的方向向量(1,k)与斜率之间的关系吗
问题5的设计是为了探究斜率与方向向量的关系,是直线方向的表示要素间关系的进一步总结,体现数学内部的知识联系,使得知识的呈现更具有逻辑性和整体性。考虑到本节的重点是倾斜角与斜率的探究,因此这里的探究以具体问题的形式呈现,一方面是为了给学生的探究提供方向性,另一方面是作为斜率的简单应用。
教学过程
(五)初步应用,巩固新知
【例1】如图,已知求直线的斜率,并判断这些
直线的倾斜角是锐角还是钝角.
【例2】如图为斜拉的钢丝锁抽象出来的部分直线,比较它们的倾斜角以及斜率的大小 .
教学过程
(五)初步应用,巩固新知
【例1】如图,已知求直线的斜率,并判断这些
直线的倾斜角是锐角还是钝角.
【例2】如图为斜拉的钢丝锁抽象出来的部分直线,比较它们的倾斜角以及斜率的大小 .
例1一方面考察了斜率公式的掌握,另一方面考察了斜率与倾斜角的联系,也是一个从形到数再到形的过程,让学生知道不仅要会用代数语言表示几何特征,还要会把代数运算得出的结果翻译成几何结论,体现了坐标法中把几何问题代数化,再通过代数运算研究几何性质的思想。
教学过程
(五)初步应用,巩固新知
【例1】如图,已知求直线的斜率,并判断这些
直线的倾斜角是锐角还是钝角.
【例2】如图为斜拉的钢丝锁抽象出来的部分直线,比较它们的倾斜角以及斜率的大小 .
例1一方面考察了斜率公式的掌握,另一方面考察了斜率与倾斜角的联系,也是一个从形到数再到形的过程,让学生知道不仅要会用代数语言表示几何特征,还要会把代数运算得出的结果翻译成几何结论,体现了坐标法中把几何问题代数化,再通过代数运算研究几何性质的思想。
通过对斜拉索所在直线倾斜角和斜率的大小比较,一方面加深倾斜角概念的理解,另一方面考察随着倾斜角的变化斜率变化的趋势。
教学过程
(六)学有所思,形成结构
【问题6】我们的研究思路是什么?用到了什么数学思想方法?
问题6是对本节课的研究框架进行的梳理,在这个梳理的过程中,一方面让学生重现研究过程,初步体会坐标法的研究思路,另一方面结合具体研究内容渗透相关的数学思想方法,如数形结合、从特殊到一般、转化化归等等。
感谢观看
