浙江省湖州市2023年初中学业水平考试数学真题(含答案)
文档属性
| 名称 | 浙江省湖州市2023年初中学业水平考试数学真题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 820.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-13 16:47:39 | ||
图片预览




文档简介
浙江省2023年初中学业水平考试(湖州市)
数学试题卷
友情提示:
1.全卷分卷Ⅰ与卷Ⅱ两部分,考试时间为120分钟,试卷满分为120分.
2.试题卷中所有试题的答案填涂或书写在答题卷的相应位置,写在试题卷上无效.
3.请仔细审题,细心答题,相信你一定会有出色的表现!
4.参考公式:抛物线的顶点坐标是.
卷 Ⅰ
一、选择题(本题有10小题,每小题3分,共30分)
下面每小题给出的四个选项中,只有一个是正确的.请选出各题中一个最符合题意的选项,并在答题卷上将相应题次中对应字母的方框涂黑,不选、多选、错选均不给分.
1.下列各数中,最小的数是
A. B. C. D.
2.计算的结果是
A. B. C. D.
3.国家互联网信息办公室2023年5月23日发布的《数字中国发展报告(2022年)》显示,2022年我国数字经济规模达502000亿元.用科学记数法表示502000,正确的是
A. B. C. D.
(
(第
4
题)
主视图
俯视图
左视图
)4.已知某几何体的三视图如图所示,则该几何体可能是
A. B.
C. D.
5.若分式的值为,则的值是
A. B. C. D.
(
(第
6
题)
)6.如图,点,,在⊙上,连结,,,.若,则的度数是
A. B.
C. D.
(
某住宅小区6月1日~6月5日每天用水量统计图
(第7题)
)7.某住宅小区6月1日~6月5日每天用水量情况如图所示,那么这 5天平均每天的用水量是
A. 25立方米 B. 30立方米
C. 32立方米 D. 35立方米
8.某品牌新能源汽车2020年的销售量为20万辆,随着消费人群的不断增多,该品牌新能源汽车的销售量逐年递增,2022年的销售量比2020年增加了31.2万辆.如果设从2020年到2022年该品牌新能源汽车销售量的平均年增长率为x,那么可列出方程是
A. B.
C. D.
(
(第9题)
)9.如图,已知,以点为圆心,适当长为半径作圆弧,与角的两边分别交于,两点,分别以点,为圆心,大于长为半径作圆弧,两条圆弧交于内一点,连结,过点作直线∥,交于点,过点作直线∥,交于点.若,cm,则四边形的面积是
A. B.
C. D.
10.已知在平面直角坐标系中,正比例函数()的图象与反比例函数()的图象的两个交点中,有一个交点的横坐标为1,点(,)和点(,)在函数的图象上(且),点(,)和点(,)在函数的图象上.当与的积为负数时,的取值范围是
A. 或 B. 或
C. 或 D. 或
卷 Ⅱ
二、填空题(本题有6小题,每小题4分,共24分)
(
(第13题)
)11.计算:= ▲ .
12.在一个不透明的箱子里放有7个红球和3个黑球,它们除颜色外其余都相同.从这个箱子里随机摸出一个球,摸出的球是红球的概率是 ▲ .
13.如图,是⊙的半径,弦于点,连结.若⊙的半径为5cm,的长为8cm,则的长是 ▲ cm.
14.已知,是两个连续整数,,则的值是 ▲ .
(
(第15题)
)15.某数学兴趣小组测量校园内一棵树的高度,采用以下方法:如图,把支架()放在离树()适当距离的水平地面上的点处,再把镜子水平放在支架()上的点处,然后沿着直线后退至点处,这时恰好在镜子里看到树的顶端,再用皮尺分别测量,,,观测者目高()的长,利用测得的数据可以求出这棵树的高度.已知于点,于点,于点,米,米,米,米,则这棵树的高度(的长)是 ▲ 米.
(
(第16题)
)16.如图,标号为①,②,③,④的四个直角三角形和标号为⑤的正方形恰好拼成对角互补的四边形,相邻图形之间互不重叠也无缝隙,①和②分别是等腰Rt△和等腰Rt△,③和④分别是Rt△和Rt△,⑤是正方形,直角顶点,,,分别在边,,,上.
(1)若cm,cm,则的长是 ▲ cm.
(2)若,则的值是 ▲ .
(
P
2
)三、解答题(本题有8小题,共66分)
17.(本小题6分)
计算:.
18.(本小题6分)
(
(第19题)
)解一元一次不等式组
19.(本小题6分)
如图,在△中,,于点,点为的中点,连结.已知,,求,的长.
20.(本小题8分)
4月23日是世界读书日.为了解学生的阅读喜好,丰富学校图书资源,某校将课外书籍设置了四类:文学类、科技类、艺术类、其他类,随机抽查了部分学生,要求每名学生从中选择自己最喜欢的一类,将抽查结果绘制成如下统计图(不完整).
(
(第20题)
被抽查学生最喜欢的书籍种类的
条形统计图
被抽查学生最喜欢的书籍种类的
扇形统计图
)
请根据图中信息解答下列问题:
(1)求被抽查的学生人数,并求出扇形统计图中的值.
(2)请将条形统计图补充完整.(温馨提示:请画在答题卷相对应的图上)
(3)若该校共有1200名学生,根据抽查结果,试估计全校最喜欢“文学类”书籍的学生人数.
(
(第21题)
)21.(本小题8分)
如图,在Rt△中,,点在边上,以点为圆心,为半径的半圆与斜边相切于点,交于点,连结.
(1)求证:.
(2)已知,,求的长.
22.(本小题10分)
某水产经销商以每千克30元的价格购进一批某品种淡水鱼,由销售经验可知,这种淡水鱼的日销售量(千克)与销售价格(元/千克)()存在一次函数关系,部分数据如下表所示:
销售价格(元/千克) 50 40
日销售量(千克) 100 200
(1)试求出关于的函数表达式.
(2)设该经销商销售这种淡水鱼的日销售利润为元,如果不考虑其他因素,求当销售价格为多少时,日销售利润最大?最大的日销售利润是多少元?
23.(本小题10分)
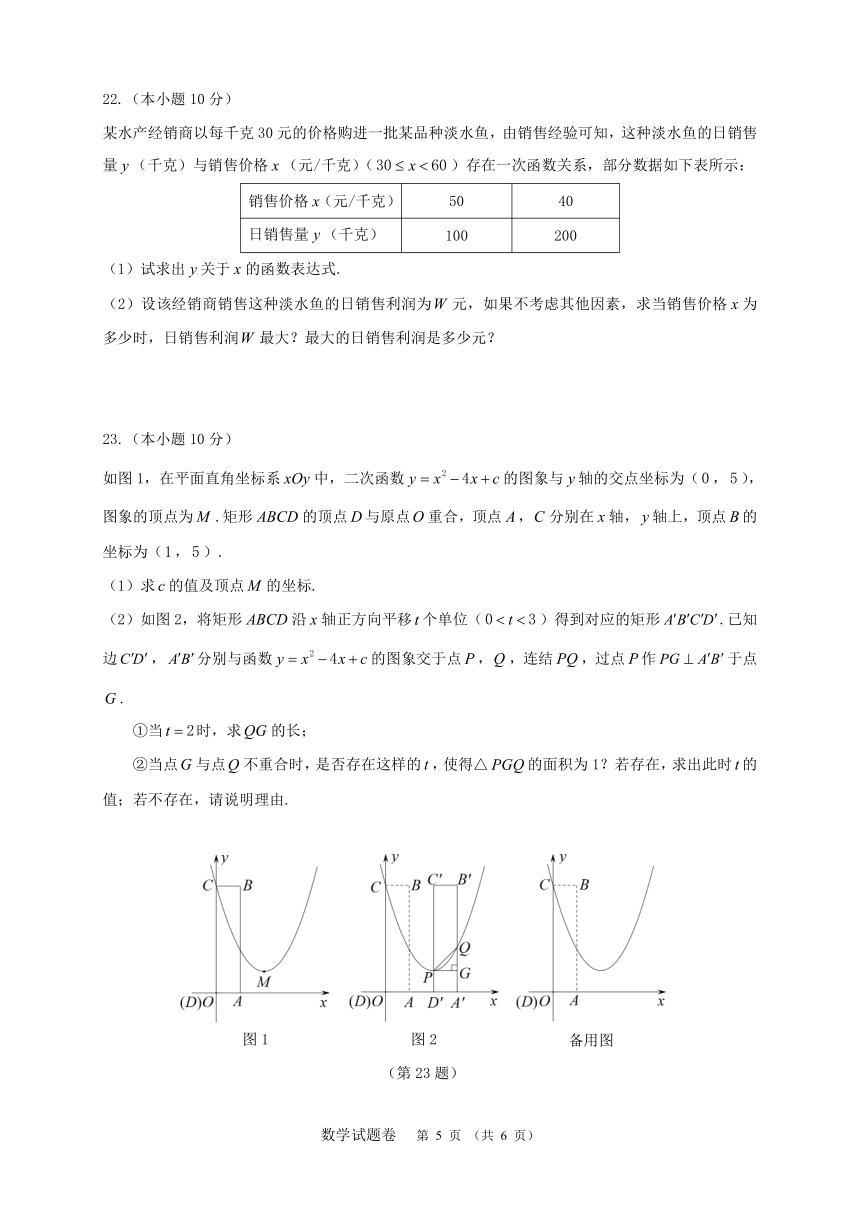
如图1,在平面直角坐标系中,二次函数的图象与轴的交点坐标为(,),图象的顶点为.矩形的顶点与原点重合,顶点,分别在轴,轴上,顶点的坐标为(,).
(1)求的值及顶点的坐标.
(2)如图2,将矩形沿轴正方向平移个单位()得到对应的矩形.已知边,分别与函数的图象交于点,,连结,过点作于点.
①当时,求的长;
②当点与点不重合时,是否存在这样的,使得△的面积为1?若存在,求出此时的值;若不存在,请说明理由.
(
(第23题)
图1
图2
备用图
)
24.(本小题12分)
【特例感知】
(1)如图1,在正方形中,点在边的延长线上,连结,过点作,交的延长线于点.求证:△≌△.
【变式求异】
(2)如图2,在Rt△中,,点在边上,过点作,交于点,点在边的延长线上,连结,过点作,交射线于点.已知,,,求的值.
【拓展应用】
(3)如图3,在Rt△中,,点在边的延长线上,点在边上(不与点,重合),连结,以为顶点作,的边交射线于点.若,(,是常数),求的值(用含,的代数式表示).
(
图2
(第24题)
图1
图3
)
浙江省2023年初中学业水平考试(湖州市)
数学参考答案及评分标准
一、选择题(每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C D A C B D B D
二、填空题(每小题4分,共24分)
11. 12. 13.
14. 15. 16.(1) (2) (每空2分)
三、解答题(共66分)
17.(本小题6分)
解 原式= ……2分
= ……2分
=. ……2分
18.(本小题6分)
解 解不等式①,得, ……2分
解不等式②,得, ……2分
所以原不等式组的解是. ……2分
19.(本小题6分)
解 ∵,于点,
∴. ……2分
∵,
∴. ……1分
∵于点,
∴,
∴在Rt△中,. ……1分
∵,
∴, ……1分
∵为的中点,
∴. ……1分(其他方法酌情给分)
20.(本小题8分)
解(1)被抽查的学生人数是 (人).……2分
(
(第
20
题)
) ∵, ……1分
∴扇形统计图中的值是40. ……1分
(2)∵ (人),
∴ 补全的条形统计图如图所示. ……2分
(3)∵(人), ……2分
∴ 估计全校最喜欢“文学类”书籍的学生人数共有360人.
21.(本小题8分)
(
(第
21
题)
)(1) 证明 如图,连结,
∵半圆与相切于点,
∴. ……2分
∵,
∴,
∵,,
∴Rt△≌Rt△(). ……1分
∴. ……1分
(2) 解 如图,∵,,
∴,
∵Rt△≌Rt△,
∴. ……1分
∵,
∴, ……1分
∴. ……2分(其他方法酌情给分)
22.(本小题10分)
解 (1)因为是的一次函数,所以设所求表达式为().
将,和,分别代入上式,
得 ……2分
解得 ……2分
所以关于的函数表达式是. ……1分
(2). ……1分
当时,在的范围内, ……2分
取到最大值,最大值是. ……2分
答:销售价格为每千克元时,日销售利润最大,最大日销售利润是2250元.
23.(本小题10分)
解 (1) ∵二次函数的图象与轴的交点坐标为(,),
∴, ……1分
∴,
∴顶点的坐标是(,). ……2分
(2)① ∵在轴上,的坐标为(,),
∴点的坐标是(,).
当时,,的坐标分别是(,),(,).
当时,,即点的纵坐标是. ……1分
当时,,即点的纵坐标是.
∵,
∴点的纵坐标是, ……1分
∴ . ……1分
(
(第23题图1)
)② 存在.理由如下:
∵△的面积为1,,
∴.
根据题意,得,的坐标分别是
(,),(,).
如图1,当点在点的上方时,
,
(
(第23题图2)
)此时(在的范围内). ……2分
如图2,当点在点的下方时,
,
此时(在的范围内). ……2分
∴或. (其他方法酌情给分)
24.(本小题12分)
(1)证明 在正方形中,
,, ……1分
所以, ……1分
∵,
∴,
∴, ……1分
∴△≌△(). ……1分
(
(第24题图1)
) (2)如图1,作于点,
∵,,
∴四边形是矩形,
∴,,
∵,
∴,
∴,
∵,
∴△∽△, ……2分
∴.
∵,,,
∴,
∵,
∴. ……1分
∵,
∴∥,
∴△∽△,
∴,
∴, ……1分
∴. ……1分
(3)∵,,
∴,
∴.
∵,
(
(第24题图2)
)∴.
如图2,作于点,
∵,
∴,
∴.
∵,
∴,
∴,
∵,
∴△∽△, ……1分
∴.
∵,,
∴△∽△,
∴,
∴,
∴. ……2分(其他方法酌情给分)
数学试题卷 第 1 页 (共 6 页)
数学试题卷
友情提示:
1.全卷分卷Ⅰ与卷Ⅱ两部分,考试时间为120分钟,试卷满分为120分.
2.试题卷中所有试题的答案填涂或书写在答题卷的相应位置,写在试题卷上无效.
3.请仔细审题,细心答题,相信你一定会有出色的表现!
4.参考公式:抛物线的顶点坐标是.
卷 Ⅰ
一、选择题(本题有10小题,每小题3分,共30分)
下面每小题给出的四个选项中,只有一个是正确的.请选出各题中一个最符合题意的选项,并在答题卷上将相应题次中对应字母的方框涂黑,不选、多选、错选均不给分.
1.下列各数中,最小的数是
A. B. C. D.
2.计算的结果是
A. B. C. D.
3.国家互联网信息办公室2023年5月23日发布的《数字中国发展报告(2022年)》显示,2022年我国数字经济规模达502000亿元.用科学记数法表示502000,正确的是
A. B. C. D.
(
(第
4
题)
主视图
俯视图
左视图
)4.已知某几何体的三视图如图所示,则该几何体可能是
A. B.
C. D.
5.若分式的值为,则的值是
A. B. C. D.
(
(第
6
题)
)6.如图,点,,在⊙上,连结,,,.若,则的度数是
A. B.
C. D.
(
某住宅小区6月1日~6月5日每天用水量统计图
(第7题)
)7.某住宅小区6月1日~6月5日每天用水量情况如图所示,那么这 5天平均每天的用水量是
A. 25立方米 B. 30立方米
C. 32立方米 D. 35立方米
8.某品牌新能源汽车2020年的销售量为20万辆,随着消费人群的不断增多,该品牌新能源汽车的销售量逐年递增,2022年的销售量比2020年增加了31.2万辆.如果设从2020年到2022年该品牌新能源汽车销售量的平均年增长率为x,那么可列出方程是
A. B.
C. D.
(
(第9题)
)9.如图,已知,以点为圆心,适当长为半径作圆弧,与角的两边分别交于,两点,分别以点,为圆心,大于长为半径作圆弧,两条圆弧交于内一点,连结,过点作直线∥,交于点,过点作直线∥,交于点.若,cm,则四边形的面积是
A. B.
C. D.
10.已知在平面直角坐标系中,正比例函数()的图象与反比例函数()的图象的两个交点中,有一个交点的横坐标为1,点(,)和点(,)在函数的图象上(且),点(,)和点(,)在函数的图象上.当与的积为负数时,的取值范围是
A. 或 B. 或
C. 或 D. 或
卷 Ⅱ
二、填空题(本题有6小题,每小题4分,共24分)
(
(第13题)
)11.计算:= ▲ .
12.在一个不透明的箱子里放有7个红球和3个黑球,它们除颜色外其余都相同.从这个箱子里随机摸出一个球,摸出的球是红球的概率是 ▲ .
13.如图,是⊙的半径,弦于点,连结.若⊙的半径为5cm,的长为8cm,则的长是 ▲ cm.
14.已知,是两个连续整数,,则的值是 ▲ .
(
(第15题)
)15.某数学兴趣小组测量校园内一棵树的高度,采用以下方法:如图,把支架()放在离树()适当距离的水平地面上的点处,再把镜子水平放在支架()上的点处,然后沿着直线后退至点处,这时恰好在镜子里看到树的顶端,再用皮尺分别测量,,,观测者目高()的长,利用测得的数据可以求出这棵树的高度.已知于点,于点,于点,米,米,米,米,则这棵树的高度(的长)是 ▲ 米.
(
(第16题)
)16.如图,标号为①,②,③,④的四个直角三角形和标号为⑤的正方形恰好拼成对角互补的四边形,相邻图形之间互不重叠也无缝隙,①和②分别是等腰Rt△和等腰Rt△,③和④分别是Rt△和Rt△,⑤是正方形,直角顶点,,,分别在边,,,上.
(1)若cm,cm,则的长是 ▲ cm.
(2)若,则的值是 ▲ .
(
P
2
)三、解答题(本题有8小题,共66分)
17.(本小题6分)
计算:.
18.(本小题6分)
(
(第19题)
)解一元一次不等式组
19.(本小题6分)
如图,在△中,,于点,点为的中点,连结.已知,,求,的长.
20.(本小题8分)
4月23日是世界读书日.为了解学生的阅读喜好,丰富学校图书资源,某校将课外书籍设置了四类:文学类、科技类、艺术类、其他类,随机抽查了部分学生,要求每名学生从中选择自己最喜欢的一类,将抽查结果绘制成如下统计图(不完整).
(
(第20题)
被抽查学生最喜欢的书籍种类的
条形统计图
被抽查学生最喜欢的书籍种类的
扇形统计图
)
请根据图中信息解答下列问题:
(1)求被抽查的学生人数,并求出扇形统计图中的值.
(2)请将条形统计图补充完整.(温馨提示:请画在答题卷相对应的图上)
(3)若该校共有1200名学生,根据抽查结果,试估计全校最喜欢“文学类”书籍的学生人数.
(
(第21题)
)21.(本小题8分)
如图,在Rt△中,,点在边上,以点为圆心,为半径的半圆与斜边相切于点,交于点,连结.
(1)求证:.
(2)已知,,求的长.
22.(本小题10分)
某水产经销商以每千克30元的价格购进一批某品种淡水鱼,由销售经验可知,这种淡水鱼的日销售量(千克)与销售价格(元/千克)()存在一次函数关系,部分数据如下表所示:
销售价格(元/千克) 50 40
日销售量(千克) 100 200
(1)试求出关于的函数表达式.
(2)设该经销商销售这种淡水鱼的日销售利润为元,如果不考虑其他因素,求当销售价格为多少时,日销售利润最大?最大的日销售利润是多少元?
23.(本小题10分)
如图1,在平面直角坐标系中,二次函数的图象与轴的交点坐标为(,),图象的顶点为.矩形的顶点与原点重合,顶点,分别在轴,轴上,顶点的坐标为(,).
(1)求的值及顶点的坐标.
(2)如图2,将矩形沿轴正方向平移个单位()得到对应的矩形.已知边,分别与函数的图象交于点,,连结,过点作于点.
①当时,求的长;
②当点与点不重合时,是否存在这样的,使得△的面积为1?若存在,求出此时的值;若不存在,请说明理由.
(
(第23题)
图1
图2
备用图
)
24.(本小题12分)
【特例感知】
(1)如图1,在正方形中,点在边的延长线上,连结,过点作,交的延长线于点.求证:△≌△.
【变式求异】
(2)如图2,在Rt△中,,点在边上,过点作,交于点,点在边的延长线上,连结,过点作,交射线于点.已知,,,求的值.
【拓展应用】
(3)如图3,在Rt△中,,点在边的延长线上,点在边上(不与点,重合),连结,以为顶点作,的边交射线于点.若,(,是常数),求的值(用含,的代数式表示).
(
图2
(第24题)
图1
图3
)
浙江省2023年初中学业水平考试(湖州市)
数学参考答案及评分标准
一、选择题(每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C D A C B D B D
二、填空题(每小题4分,共24分)
11. 12. 13.
14. 15. 16.(1) (2) (每空2分)
三、解答题(共66分)
17.(本小题6分)
解 原式= ……2分
= ……2分
=. ……2分
18.(本小题6分)
解 解不等式①,得, ……2分
解不等式②,得, ……2分
所以原不等式组的解是. ……2分
19.(本小题6分)
解 ∵,于点,
∴. ……2分
∵,
∴. ……1分
∵于点,
∴,
∴在Rt△中,. ……1分
∵,
∴, ……1分
∵为的中点,
∴. ……1分(其他方法酌情给分)
20.(本小题8分)
解(1)被抽查的学生人数是 (人).……2分
(
(第
20
题)
) ∵, ……1分
∴扇形统计图中的值是40. ……1分
(2)∵ (人),
∴ 补全的条形统计图如图所示. ……2分
(3)∵(人), ……2分
∴ 估计全校最喜欢“文学类”书籍的学生人数共有360人.
21.(本小题8分)
(
(第
21
题)
)(1) 证明 如图,连结,
∵半圆与相切于点,
∴. ……2分
∵,
∴,
∵,,
∴Rt△≌Rt△(). ……1分
∴. ……1分
(2) 解 如图,∵,,
∴,
∵Rt△≌Rt△,
∴. ……1分
∵,
∴, ……1分
∴. ……2分(其他方法酌情给分)
22.(本小题10分)
解 (1)因为是的一次函数,所以设所求表达式为().
将,和,分别代入上式,
得 ……2分
解得 ……2分
所以关于的函数表达式是. ……1分
(2). ……1分
当时,在的范围内, ……2分
取到最大值,最大值是. ……2分
答:销售价格为每千克元时,日销售利润最大,最大日销售利润是2250元.
23.(本小题10分)
解 (1) ∵二次函数的图象与轴的交点坐标为(,),
∴, ……1分
∴,
∴顶点的坐标是(,). ……2分
(2)① ∵在轴上,的坐标为(,),
∴点的坐标是(,).
当时,,的坐标分别是(,),(,).
当时,,即点的纵坐标是. ……1分
当时,,即点的纵坐标是.
∵,
∴点的纵坐标是, ……1分
∴ . ……1分
(
(第23题图1)
)② 存在.理由如下:
∵△的面积为1,,
∴.
根据题意,得,的坐标分别是
(,),(,).
如图1,当点在点的上方时,
,
(
(第23题图2)
)此时(在的范围内). ……2分
如图2,当点在点的下方时,
,
此时(在的范围内). ……2分
∴或. (其他方法酌情给分)
24.(本小题12分)
(1)证明 在正方形中,
,, ……1分
所以, ……1分
∵,
∴,
∴, ……1分
∴△≌△(). ……1分
(
(第24题图1)
) (2)如图1,作于点,
∵,,
∴四边形是矩形,
∴,,
∵,
∴,
∴,
∵,
∴△∽△, ……2分
∴.
∵,,,
∴,
∵,
∴. ……1分
∵,
∴∥,
∴△∽△,
∴,
∴, ……1分
∴. ……1分
(3)∵,,
∴,
∴.
∵,
(
(第24题图2)
)∴.
如图2,作于点,
∵,
∴,
∴.
∵,
∴,
∴,
∵,
∴△∽△, ……1分
∴.
∵,,
∴△∽△,
∴,
∴,
∴. ……2分(其他方法酌情给分)
数学试题卷 第 1 页 (共 6 页)
同课章节目录
