苏科版九年级数学上册3.2 中位数与众数 课件(共30张PPT)
文档属性
| 名称 | 苏科版九年级数学上册3.2 中位数与众数 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 39.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-13 00:00:00 | ||
图片预览










文档简介
(共30张PPT)
3.2中位数与众数
第3章数据的集中趋势与离散程度
教学目标
01
理解中位数的概念,能准确识别出中位数
02
理解众数的概念,能准确识别出众数
03
能具体情况具体分析,从平均数、中位数、众数中选取合适的数刻画一组数据的集中趋势
中位数
01
二、定义
情境引入Part1
Q1:在“献爱心”捐款活动中,某校九年级(1)班第3小组11名同学的捐款数如下(单位:元):
4,4,2,3,3,5,7,6,8,10,91。
(1)这个小组平均每名同学捐款多少元?
(2)这个平均数能较好地反映该组同学捐款数的“集中趋势”吗
【分析】(1)=13(元);
01
二、定义
情境引入Part1
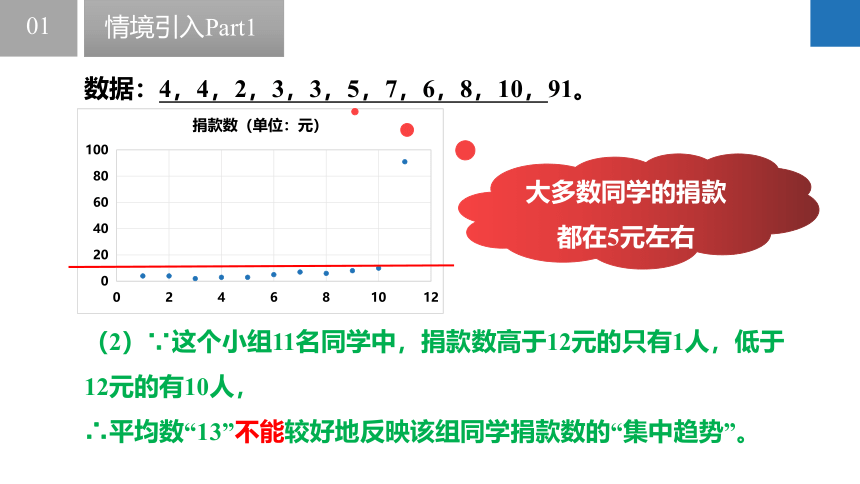
(2)∵这个小组11名同学中,捐款数高于12元的只有1人,低于12元的有10人,
∴平均数“13”不能较好地反映该组同学捐款数的“集中趋势”。
数据:4,4,2,3,3,5,7,6,8,10,91。
大多数同学的捐款都在5元左右
01
二、定义
情境引入Part2
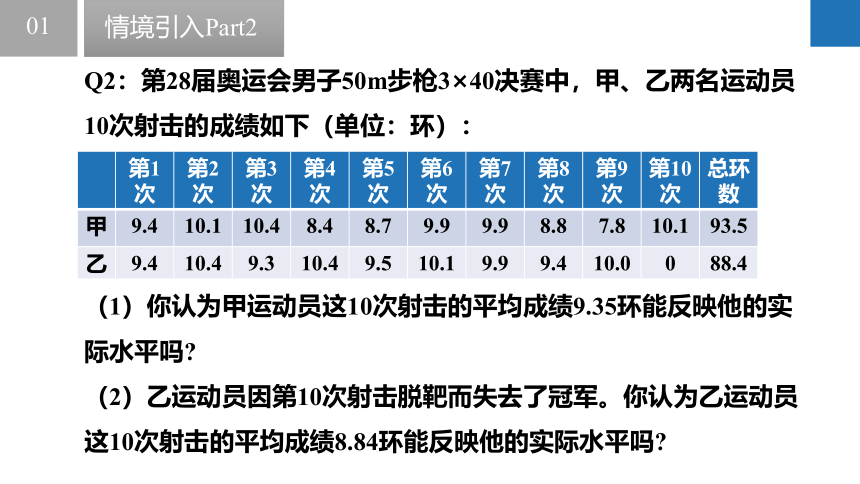
Q2:第28届奥运会男子50m步枪3×40决赛中,甲、乙两名运动员10次射击的成绩如下(单位:环):
(1)你认为甲运动员这10次射击的平均成绩9.35环能反映他的实际水平吗
(2)乙运动员因第10次射击脱靶而失去了冠军。你认为乙运动员这10次射击的平均成绩8.84环能反映他的实际水平吗
第1次 第2次 第3次 第4次 第5次 第6次 第7次 第8次 第9次 第10次 总环数
甲 9.4 10.1 10.4 8.4 8.7 9.9 9.9 8.8 7.8 10.1 93.5
乙 9.4 10.4 9.3 10.4 9.5 10.1 9.9 9.4 10.0 0 88.4
01
二、定义
情境引入Part2
第1次 第2次 第3次 第4次 第5次 第6次 第7次 第8次 第9次 第10次 总环数
甲 9.4 10.1 10.4 8.4 8.7 9.9 9.9 8.8 7.8 10.1 93.5
乙 9.4 10.4 9.3 10.4 9.5 10.1 9.9 9.4 10.0 0 88.4
【分析】(1)∵甲运动员10次射击的成绩中,高于9.35环的有6次,低于9.35环的有4次,
∴数据“9.35”能较好地反映这组数据的集中趋势;
(2)∵乙运动员10次射击的成绩中,高于8.84环的有9次,低于8.84环的只有1次,
∴数据“8.84”不能较好地反映这组数据的集中趋势。
二、定义
情境引入
02
知识精讲
平均数的大小与一组数据中的每个数据都有关系~
当一组数据中所有数据的大小差异不大,通常用平均数来描述这组数据的集中趋势;
当一组数据中个别数据与其他数据的大小差异很大,那么平均数就不能较好地反映这组数据的集中趋势。
eg:“Q1”中的“91”,“Q2”中乙的“0”。
二、定义
情境引入
02
知识精讲
“Q1”中11名同学的捐款数“4,4,2,3,3,5,7,6,8,10,91”的集中趋势怎样来描述呢
【分析】将11名同学的捐款数按从小到大的顺序排列:
2,3,3,4,4,5,6,7,8,10,91。
处于中间位置的数是5,我们用“5”来描述这组数据的集中趋势。
二、定义
情境引入
02
知识精讲
“Q2”中乙运动员的10次射击成绩“9.4,10.4,9.3,10.4,9.5,10.1,9.9,9.4,10.0,0”的集中趋势怎样来描述呢
【分析】将乙运动员的10次射击成绩按从小到大的顺序排列:
0,9.3,9.4,9.4,9.5,9.9,10.0,10.1,10.4,10.4。
处于中间位置的数是9.5和9.9,我们用这两个数的平均数“9.7”来描述这组数据的集中趋势。
二、定义
情境引入
02
知识精讲
中位数
一般地,将一组数据按大小顺序排列,
1.如果数据的个数是奇数,那么处于中间位置的数叫做这组数据的中位数;
eg:“Q1”中11名同学的捐款数的中位数是5;
“Q2”中乙运动员的10次射击成绩的中位数是9.7。
2.如果数据的个数是偶数,那么处于中间位置的两个数的平均数叫做这组数据的中位数。
二、定义
情境引入
02
知识精讲
中位数
当一组数据中个别数据与其他数据的大小差异很大时,通常用中位数来描述这组数据的集中趋势。
例1、已知一组数据12、4、8、m、10,它们的平均数是8,则这一组数据的中位数为( )
A.4 B.8 C.10 D.12
03
典例精析
【分析】由题意知:12+4+8+m+10=5×8,
解得:m=6,
则这组数据为4、6、8、10、12,
所以这组数据的中位数为8。
B
例2、在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如图所示,则这些运动员成绩的中位数为( )
A.160 B.165 C.170 D.175
03
典例精析
【分析】把这些数从小到大排列,中位数是第8个数,则这些运动员成绩的中位数为165cm。
B
众数
01
二、定义
情境引入
小明在校内抽样调查了30名男同学的衬衫尺码,数据如下(单位:cm):
你认为学校商店应多采购哪种尺码的男衬衫 说说你的理由。
领口大小 37 38 39 40 41 42
人数 3 6 14 5 1 1
【分析】穿领口大小为39cm的衬衫的人数最多,应多采购这种尺码的衬衫。
二、定义
情境引入
02
知识精讲
众数
一组数据中出现次数最多的数据叫做这组数据的众数。
eg:在“情境引入”中,数据“39”出现的次数最多,“39”是这组数据的众数。
当一组数据中有较多的重复数据时,常用众数来描述这组数据的集中趋势。
例1、小明在班上做节约用水意识的调查,收集了班上7位同学家里上个月的用水量(单位:吨)如下:4,4,6,7,8,9,10。他发现,若去掉其中两个数据后,这组数据的中位数,众数保持不变,则去掉的两个数可能是( )
A.4,10 B.4,9 C.7,8 D.6,8
03
典例精析
【分析】∵4,4,6,7,8,9,10的众数是4,中位数是7,
∴去掉的两个数可能是是6,8或6,9或6,10,不能去掉的数是4和7。
D
例2、某校积极鼓励学生参加志愿者活动,表列出了随机抽取的100名学生一周参与志愿者活动的时间情况:
根据表中数据,下列说法中不正确的是( )
A.表中x的值为32
B.这组数据的众数是2h
C.这组数据的中位数是2h
D.这组数据的平均数是1.7h
03
典例精析
【分析】由题意看得:x=100-20-38-8-2=32,正确;
这组数据中2出现的次数最多,故众数是2h,正确;
这组数据的中位数是=1.5(h),不正确;
这组数据的平均数是=1.7(h),正确。
C
参与志愿者活动的时间(h) 1 1.5 2 2.5 3
参与志愿者活动的时间(人) 20 x 38 8 2
二、定义
情境引入
02
知识精讲
某公司职工的月工资情况如下(单位:元):
(1)该公司职工月工资的平均数、中位数和众数分别为多少?
(2)如果你是该公司的一员,那么会更加关注其中的哪一个数据?
月工资 20000 12000 8000 6000 3000 2000 1800 1500 1200
人数 1 (总经理) 2 (副总经理) 5 (部门经理) 10 17 23 28 10 4
【分析】(1)平均数:=3112(元),
二、定义
情境引入
02
知识精讲
月工资 20000 12000 8000 6000 3000 2000 1800 1500 1200
人数 1 (总经理) 2 (副总经理) 5 (部门经理) 10 17 23 28 10 4
中位数:
一共100人,处于中间位置的数是2000和2000,两数的平均数是2000,即中位数为2000元,
众数:1800元;
二、定义
情境引入
02
知识精讲
(2)如果我是普通职工,我更关注自己的收入在职工群体中的位置,感兴趣的是职工月工资的中位数;
如果我是工会主席,我更关注多数职工利益,感兴趣的是职工月工资的众数;
如果我是总经理,我更关注职工月工资总额,感兴趣的是职工月工资的平均数。
平均数、中位数、众数都能刻画数据的集中趋势,在实际应用中,应根据需要恰当地进行选择。
二、定义
情境引入
02
知识精讲
当一组数据中所有数据的大小差异不大,通常用平均数来描述这组数据的集中趋势;
当一组数据中个别数据与其他数据的大小差异很大时,通常用中位数来描述这组数据的集中趋势;
当一组数据中有较多的重复数据时,常用众数来描述这组数据的集中趋势。
集中趋势
例3、为深入学习贯彻党的二十大精神,某校九年级的两个班(每班50人)开展了“学习二十大 奋进新征程”知识竞赛,德育处对其成绩进行了统计,绘制了如下统计图:
请根据以上信息,解答下列问题:
03
典例精析
(1)将表格补充完整:
03
典例精析
平均数(分) 中位数(分) 众数
(分)
一班 80.8 ______ 70
二班 ______ 80 ______
解:(1)一班的中位数:=70(分)。
二班的平均数:60×10%+70×20%+80×40%+90×20%+100×10%=80(分),
二班的众数:80分;
70
80
80
(2)请你对两个班的成绩作出评价(从“平均数”,“中位数”或“众数”中的一个方面评价即可)。
03
典例精析
平均数(分) 中位数(分) 众数
(分)
一班 80.8 ______ 70
二班 ______ 80 ______
70
80
80
(2)从平均数来看:一班,二班知识竞赛成绩的平均数分别为80.8分,80分,说明一班成绩的平均数大于二班的平均数。
(2)请你对两个班的成绩作出评价(从“平均数”,“中位数”或“众数”中的一个方面评价即可)。
03
典例精析
平均数(分) 中位数(分) 众数
(分)
一班 80.8 ______ 70
二班 ______ 80 ______
70
80
80
从中位数来看:一班,二班知识竞赛成绩的中位数分别为70分,80分,说明二班知识竞赛成绩的中位数大于一班知识竞赛成绩的中位数。
(2)请你对两个班的成绩作出评价(从“平均数”,“中位数”或“众数”中的一个方面评价即可)。
03
典例精析
平均数(分) 中位数(分) 众数
(分)
一班 80.8 ______ 70
二班 ______ 80 ______
70
80
80
从众数来看:一班,二班知识竞赛成绩的众数分别为70分,80分,说明一班知识竞赛成绩中70分最多,二班知识竞赛成绩中80分最多。
课后总结
一般地,将一组数据按大小顺序排列,
1.如果数据的个数是奇数,那么处于中间位置的数叫做这组数据的中位数;
2.如果数据的个数是偶数,那么处于中间位置的两个数的平均数叫做这组数据的中位数。
一组数据中出现次数最多的数据叫做这组数据的众数。
当一组数据中所有数据的大小差异不大,通常用平均数来描述这组数据的集中趋势;
当一组数据中个别数据与其他数据的大小差异很大时,通常用中位数来描述这组数据的集中趋势;
当一组数据中有较多的重复数据时,常用众数来描述这组数据的集中趋势。
3.2中位数与众数
3.2中位数与众数
第3章数据的集中趋势与离散程度
教学目标
01
理解中位数的概念,能准确识别出中位数
02
理解众数的概念,能准确识别出众数
03
能具体情况具体分析,从平均数、中位数、众数中选取合适的数刻画一组数据的集中趋势
中位数
01
二、定义
情境引入Part1
Q1:在“献爱心”捐款活动中,某校九年级(1)班第3小组11名同学的捐款数如下(单位:元):
4,4,2,3,3,5,7,6,8,10,91。
(1)这个小组平均每名同学捐款多少元?
(2)这个平均数能较好地反映该组同学捐款数的“集中趋势”吗
【分析】(1)=13(元);
01
二、定义
情境引入Part1
(2)∵这个小组11名同学中,捐款数高于12元的只有1人,低于12元的有10人,
∴平均数“13”不能较好地反映该组同学捐款数的“集中趋势”。
数据:4,4,2,3,3,5,7,6,8,10,91。
大多数同学的捐款都在5元左右
01
二、定义
情境引入Part2
Q2:第28届奥运会男子50m步枪3×40决赛中,甲、乙两名运动员10次射击的成绩如下(单位:环):
(1)你认为甲运动员这10次射击的平均成绩9.35环能反映他的实际水平吗
(2)乙运动员因第10次射击脱靶而失去了冠军。你认为乙运动员这10次射击的平均成绩8.84环能反映他的实际水平吗
第1次 第2次 第3次 第4次 第5次 第6次 第7次 第8次 第9次 第10次 总环数
甲 9.4 10.1 10.4 8.4 8.7 9.9 9.9 8.8 7.8 10.1 93.5
乙 9.4 10.4 9.3 10.4 9.5 10.1 9.9 9.4 10.0 0 88.4
01
二、定义
情境引入Part2
第1次 第2次 第3次 第4次 第5次 第6次 第7次 第8次 第9次 第10次 总环数
甲 9.4 10.1 10.4 8.4 8.7 9.9 9.9 8.8 7.8 10.1 93.5
乙 9.4 10.4 9.3 10.4 9.5 10.1 9.9 9.4 10.0 0 88.4
【分析】(1)∵甲运动员10次射击的成绩中,高于9.35环的有6次,低于9.35环的有4次,
∴数据“9.35”能较好地反映这组数据的集中趋势;
(2)∵乙运动员10次射击的成绩中,高于8.84环的有9次,低于8.84环的只有1次,
∴数据“8.84”不能较好地反映这组数据的集中趋势。
二、定义
情境引入
02
知识精讲
平均数的大小与一组数据中的每个数据都有关系~
当一组数据中所有数据的大小差异不大,通常用平均数来描述这组数据的集中趋势;
当一组数据中个别数据与其他数据的大小差异很大,那么平均数就不能较好地反映这组数据的集中趋势。
eg:“Q1”中的“91”,“Q2”中乙的“0”。
二、定义
情境引入
02
知识精讲
“Q1”中11名同学的捐款数“4,4,2,3,3,5,7,6,8,10,91”的集中趋势怎样来描述呢
【分析】将11名同学的捐款数按从小到大的顺序排列:
2,3,3,4,4,5,6,7,8,10,91。
处于中间位置的数是5,我们用“5”来描述这组数据的集中趋势。
二、定义
情境引入
02
知识精讲
“Q2”中乙运动员的10次射击成绩“9.4,10.4,9.3,10.4,9.5,10.1,9.9,9.4,10.0,0”的集中趋势怎样来描述呢
【分析】将乙运动员的10次射击成绩按从小到大的顺序排列:
0,9.3,9.4,9.4,9.5,9.9,10.0,10.1,10.4,10.4。
处于中间位置的数是9.5和9.9,我们用这两个数的平均数“9.7”来描述这组数据的集中趋势。
二、定义
情境引入
02
知识精讲
中位数
一般地,将一组数据按大小顺序排列,
1.如果数据的个数是奇数,那么处于中间位置的数叫做这组数据的中位数;
eg:“Q1”中11名同学的捐款数的中位数是5;
“Q2”中乙运动员的10次射击成绩的中位数是9.7。
2.如果数据的个数是偶数,那么处于中间位置的两个数的平均数叫做这组数据的中位数。
二、定义
情境引入
02
知识精讲
中位数
当一组数据中个别数据与其他数据的大小差异很大时,通常用中位数来描述这组数据的集中趋势。
例1、已知一组数据12、4、8、m、10,它们的平均数是8,则这一组数据的中位数为( )
A.4 B.8 C.10 D.12
03
典例精析
【分析】由题意知:12+4+8+m+10=5×8,
解得:m=6,
则这组数据为4、6、8、10、12,
所以这组数据的中位数为8。
B
例2、在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如图所示,则这些运动员成绩的中位数为( )
A.160 B.165 C.170 D.175
03
典例精析
【分析】把这些数从小到大排列,中位数是第8个数,则这些运动员成绩的中位数为165cm。
B
众数
01
二、定义
情境引入
小明在校内抽样调查了30名男同学的衬衫尺码,数据如下(单位:cm):
你认为学校商店应多采购哪种尺码的男衬衫 说说你的理由。
领口大小 37 38 39 40 41 42
人数 3 6 14 5 1 1
【分析】穿领口大小为39cm的衬衫的人数最多,应多采购这种尺码的衬衫。
二、定义
情境引入
02
知识精讲
众数
一组数据中出现次数最多的数据叫做这组数据的众数。
eg:在“情境引入”中,数据“39”出现的次数最多,“39”是这组数据的众数。
当一组数据中有较多的重复数据时,常用众数来描述这组数据的集中趋势。
例1、小明在班上做节约用水意识的调查,收集了班上7位同学家里上个月的用水量(单位:吨)如下:4,4,6,7,8,9,10。他发现,若去掉其中两个数据后,这组数据的中位数,众数保持不变,则去掉的两个数可能是( )
A.4,10 B.4,9 C.7,8 D.6,8
03
典例精析
【分析】∵4,4,6,7,8,9,10的众数是4,中位数是7,
∴去掉的两个数可能是是6,8或6,9或6,10,不能去掉的数是4和7。
D
例2、某校积极鼓励学生参加志愿者活动,表列出了随机抽取的100名学生一周参与志愿者活动的时间情况:
根据表中数据,下列说法中不正确的是( )
A.表中x的值为32
B.这组数据的众数是2h
C.这组数据的中位数是2h
D.这组数据的平均数是1.7h
03
典例精析
【分析】由题意看得:x=100-20-38-8-2=32,正确;
这组数据中2出现的次数最多,故众数是2h,正确;
这组数据的中位数是=1.5(h),不正确;
这组数据的平均数是=1.7(h),正确。
C
参与志愿者活动的时间(h) 1 1.5 2 2.5 3
参与志愿者活动的时间(人) 20 x 38 8 2
二、定义
情境引入
02
知识精讲
某公司职工的月工资情况如下(单位:元):
(1)该公司职工月工资的平均数、中位数和众数分别为多少?
(2)如果你是该公司的一员,那么会更加关注其中的哪一个数据?
月工资 20000 12000 8000 6000 3000 2000 1800 1500 1200
人数 1 (总经理) 2 (副总经理) 5 (部门经理) 10 17 23 28 10 4
【分析】(1)平均数:=3112(元),
二、定义
情境引入
02
知识精讲
月工资 20000 12000 8000 6000 3000 2000 1800 1500 1200
人数 1 (总经理) 2 (副总经理) 5 (部门经理) 10 17 23 28 10 4
中位数:
一共100人,处于中间位置的数是2000和2000,两数的平均数是2000,即中位数为2000元,
众数:1800元;
二、定义
情境引入
02
知识精讲
(2)如果我是普通职工,我更关注自己的收入在职工群体中的位置,感兴趣的是职工月工资的中位数;
如果我是工会主席,我更关注多数职工利益,感兴趣的是职工月工资的众数;
如果我是总经理,我更关注职工月工资总额,感兴趣的是职工月工资的平均数。
平均数、中位数、众数都能刻画数据的集中趋势,在实际应用中,应根据需要恰当地进行选择。
二、定义
情境引入
02
知识精讲
当一组数据中所有数据的大小差异不大,通常用平均数来描述这组数据的集中趋势;
当一组数据中个别数据与其他数据的大小差异很大时,通常用中位数来描述这组数据的集中趋势;
当一组数据中有较多的重复数据时,常用众数来描述这组数据的集中趋势。
集中趋势
例3、为深入学习贯彻党的二十大精神,某校九年级的两个班(每班50人)开展了“学习二十大 奋进新征程”知识竞赛,德育处对其成绩进行了统计,绘制了如下统计图:
请根据以上信息,解答下列问题:
03
典例精析
(1)将表格补充完整:
03
典例精析
平均数(分) 中位数(分) 众数
(分)
一班 80.8 ______ 70
二班 ______ 80 ______
解:(1)一班的中位数:=70(分)。
二班的平均数:60×10%+70×20%+80×40%+90×20%+100×10%=80(分),
二班的众数:80分;
70
80
80
(2)请你对两个班的成绩作出评价(从“平均数”,“中位数”或“众数”中的一个方面评价即可)。
03
典例精析
平均数(分) 中位数(分) 众数
(分)
一班 80.8 ______ 70
二班 ______ 80 ______
70
80
80
(2)从平均数来看:一班,二班知识竞赛成绩的平均数分别为80.8分,80分,说明一班成绩的平均数大于二班的平均数。
(2)请你对两个班的成绩作出评价(从“平均数”,“中位数”或“众数”中的一个方面评价即可)。
03
典例精析
平均数(分) 中位数(分) 众数
(分)
一班 80.8 ______ 70
二班 ______ 80 ______
70
80
80
从中位数来看:一班,二班知识竞赛成绩的中位数分别为70分,80分,说明二班知识竞赛成绩的中位数大于一班知识竞赛成绩的中位数。
(2)请你对两个班的成绩作出评价(从“平均数”,“中位数”或“众数”中的一个方面评价即可)。
03
典例精析
平均数(分) 中位数(分) 众数
(分)
一班 80.8 ______ 70
二班 ______ 80 ______
70
80
80
从众数来看:一班,二班知识竞赛成绩的众数分别为70分,80分,说明一班知识竞赛成绩中70分最多,二班知识竞赛成绩中80分最多。
课后总结
一般地,将一组数据按大小顺序排列,
1.如果数据的个数是奇数,那么处于中间位置的数叫做这组数据的中位数;
2.如果数据的个数是偶数,那么处于中间位置的两个数的平均数叫做这组数据的中位数。
一组数据中出现次数最多的数据叫做这组数据的众数。
当一组数据中所有数据的大小差异不大,通常用平均数来描述这组数据的集中趋势;
当一组数据中个别数据与其他数据的大小差异很大时,通常用中位数来描述这组数据的集中趋势;
当一组数据中有较多的重复数据时,常用众数来描述这组数据的集中趋势。
3.2中位数与众数
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
