2.1 静电力做功与电势能 课件 (共16张PPT) 高一物理鲁科版(2019)必修三
文档属性
| 名称 | 2.1 静电力做功与电势能 课件 (共16张PPT) 高一物理鲁科版(2019)必修三 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-10-12 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
第二章 电势能与电势差
2.1 静电力做功与电势能
我们知道,在攀岩运动中,若攀岩者上升,则重力做负功;若攀岩者下降,则重力做正功。重力做功的多少与攀岩者的始末位置有关,与攀岩路径无关。
那么,电荷在静电力作用下运动,若静电力对电荷做功,与重力做功有无相似之处?
重力做功
运动路径无关
匀强电场中,电场力与重力相似,
mg
qE
电场力做功是否有相似的特点?
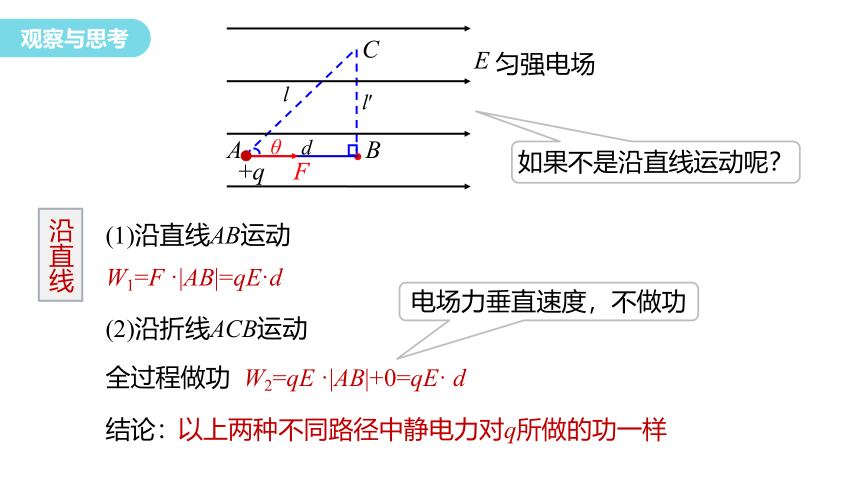
(1)如图丙所示,在电场强度为E的匀强电场中,若将一个带正电的电荷量为q的试探电荷沿电场方向从A点移动到B点,移动距离为d,则静电力做功为多少?
(2)如果将这个试探电荷从A点沿折线ACB移动到B点,则静电力做功为多少?
(3)如果试探电荷沿任一路径从A点移动到B点(如图丙中的曲线表示的路径),静电力做功又是多少?可得出什么结论。
C
A
B
如果不是沿直线运动呢?
(1)沿直线AB运动
(2)沿折线ACB运动
电场力垂直速度,不做功
结论:
以上两种不同路径中静电力对q所做的功一样
沿直线
W1=F ·|AB|=qE·d
全过程做功 W2=qE ·|AB|+0=qE· d
θ
匀强电场
E
+q
F
d
l
l′
匀强电场
E
A
B
(3)沿任一路径从A点移动到B点
+q
F
F
F
F
x1
x2
x3
x4
x1 + x2 + x3 + x4 …=
由以上的推导我们发现了什么
W1 = qE ·x1
W2 = qE ·x2
W3 = qE ·x3
|AB|
说明静电力做功与路径无关,只与初、末位置有关.
推广:非匀强电场也适用.
W4 = qE ·x4
沿曲线
(1)电荷从电场中的A点运动到了B点,路径不同,静电力做功的大小就可能不同。( )
(2)电荷从电场中的某点开始出发,运动一段时间后,又回到了该点,则静电力做功为零。( )
(3)正电荷沿着电场线方向运动,静电力对正电荷做正功;负电荷沿着电场线的反方向运动,静电力对负电荷做正功。( )
(4)电荷在电场中运动,静电力做功只与位置有关,与电荷正、负无关。
( )
×
√
√
×
1.如图所示的匀强电场中,有a、b、c三点,dab=5 cm,dbc=12 cm,其中ab沿电场方向,bc和电场方向成60°角。一个电荷量为q=4×10-8 C的正电荷从a移到b时电场力做的功为W1=1.2×10-7 J,求:
(1)匀强电场的电场强度E的大小;
答案 (1) 60 N/C (2) 2.64×10-7 J
(2)电荷从a移到c,电场力做的功W2。
一个正电荷在电场中只受到静电力F的作用,它在电场中由A点运动到B点时,静电力做了正功WAB。由动能定理可知,该电荷的动能增加了WAB。
从能量转化的角度思考,物体动能增加了,意味着另外一种形式的能量减少了。类比重力做功与重力势能的关系,这是一种什么形式的能量呢?
电荷只受静电力作用,只有静电力做功,故这种能量变化与静电力做功有关,静电力做功与重力做功特点相似:做功与路径无关,那么这种能就是势能的一种。
电势能Ep
1.概念:电荷在电场中具有的势能,这种势能称为电势能。用Ep表示。
2.大小:电荷在电场中某点的电势能,等于电荷从该点移动到零电势能点静电力所做的功。
3.电势能与静电力做功的关系:静电力做的功等于电势能的减小量,即WAB=EpA-EpB=-ΔEp。
4.电势能的相对性:选择不同的零电势能点,电荷在电场中同一点的电势能的值是不同(填“相同”或“不同”)的。
5.电势能为标量,正负值表示电势能的大小。
(1)分析正电荷只在静电力作用下从A→B运动(图甲)和从B→A运动时(图乙)静电力做功情况、动能和电势能的变化.
从A→B静电力做正功,动能增加,电势能减少
从B→A静电力做负功,动能减少,电势能增加
A
B
qE
WAB=EpA-EpB=EpA - 0
EpA=WAB
思考与讨论
mg
A
B
A
B
qE
(2)如果规定B点为零势能位置,若电荷从A移动至B静电力对电荷做功为WAB,则电荷在A点电势能是多少?
2.(多选)如图所示,在正点电荷产生的电场中的一条电场线上依次有A、B、C三点,分别把带电荷量为+q和-q的试探点电荷依次放在这三个点上,关于它们所具有的电势能,下列说法中正确的是
A.放上+q的试探点电荷时,试探点电荷在各点的电势能大小关系为EpA>EpB>EpC
B.放上+q的试探点电荷时,试探点电荷在各点的电势能大小关系为EpA<EpB<EpC
C.放上-q的试探点电荷时,试探点电荷在各点的电势能大小关系为EpA>EpB>EpC
D.放上-q的试探点电荷时,试探点电荷在各点的电势能大小关系为EpA<EpB<EpC
√
√
电势能大小的判断
1.做功判断法:无论正、负电荷,静电力做正功,电荷的电势能减小;静电力做负功,电荷的电势能增大。
2.能量守恒判断法:只有静电力做功时,电荷只有动能和电势能相互转化,总能量不变。因此,可由动能的变化确定电势能的变化。即只有静电力做功时,动能减少多少,电势能就增加多少;反之,动能增加多少,电势能就减少多少。
3.电场线法:(1)正电荷顺着电场线的方向移动时电势能逐渐减小,逆着电场线的方向移动时电势能逐渐增大;(2)负电荷顺着电场线的方向移动时电势能逐渐增大,逆着电场线的方向移动时电势能逐渐减小。
3.将带电荷量为6×10-6 C的负电荷从电场中的A点移到B点,克服静电力做了3×10-5 J的功,再从B移到C,静电力做了1.2×10-5 J的功,则:
(1)电荷从A移到C的整个过程中电势能改变了多少?
答案 (1)电势能增加了1.8×10-5 J。
(2) EpB=3×10-5 J,EpC=1.8×10-5 J。
(2)如果规定A点的电势能为零,则该电荷在B点和C点的电势能分别为多少?
(3)如果规定B点的电势能为零,则该电荷在A点和C点的电势能分别为多少?
静电力做功与电势能
静电力做功
电势能
特点:只与初末位置有关与路径无关
计算方法:W=qEdcos θ (θ为力与位移之间的夹角)
定义:电荷在电场中具有的势能
静电力做功与电势能变化的关系: WAB =EpA-EpB
电场力做正功,电势能减小
第二章 电势能与电势差
2.1 静电力做功与电势能
我们知道,在攀岩运动中,若攀岩者上升,则重力做负功;若攀岩者下降,则重力做正功。重力做功的多少与攀岩者的始末位置有关,与攀岩路径无关。
那么,电荷在静电力作用下运动,若静电力对电荷做功,与重力做功有无相似之处?
重力做功
运动路径无关
匀强电场中,电场力与重力相似,
mg
qE
电场力做功是否有相似的特点?
(1)如图丙所示,在电场强度为E的匀强电场中,若将一个带正电的电荷量为q的试探电荷沿电场方向从A点移动到B点,移动距离为d,则静电力做功为多少?
(2)如果将这个试探电荷从A点沿折线ACB移动到B点,则静电力做功为多少?
(3)如果试探电荷沿任一路径从A点移动到B点(如图丙中的曲线表示的路径),静电力做功又是多少?可得出什么结论。
C
A
B
如果不是沿直线运动呢?
(1)沿直线AB运动
(2)沿折线ACB运动
电场力垂直速度,不做功
结论:
以上两种不同路径中静电力对q所做的功一样
沿直线
W1=F ·|AB|=qE·d
全过程做功 W2=qE ·|AB|+0=qE· d
θ
匀强电场
E
+q
F
d
l
l′
匀强电场
E
A
B
(3)沿任一路径从A点移动到B点
+q
F
F
F
F
x1
x2
x3
x4
x1 + x2 + x3 + x4 …=
由以上的推导我们发现了什么
W1 = qE ·x1
W2 = qE ·x2
W3 = qE ·x3
|AB|
说明静电力做功与路径无关,只与初、末位置有关.
推广:非匀强电场也适用.
W4 = qE ·x4
沿曲线
(1)电荷从电场中的A点运动到了B点,路径不同,静电力做功的大小就可能不同。( )
(2)电荷从电场中的某点开始出发,运动一段时间后,又回到了该点,则静电力做功为零。( )
(3)正电荷沿着电场线方向运动,静电力对正电荷做正功;负电荷沿着电场线的反方向运动,静电力对负电荷做正功。( )
(4)电荷在电场中运动,静电力做功只与位置有关,与电荷正、负无关。
( )
×
√
√
×
1.如图所示的匀强电场中,有a、b、c三点,dab=5 cm,dbc=12 cm,其中ab沿电场方向,bc和电场方向成60°角。一个电荷量为q=4×10-8 C的正电荷从a移到b时电场力做的功为W1=1.2×10-7 J,求:
(1)匀强电场的电场强度E的大小;
答案 (1) 60 N/C (2) 2.64×10-7 J
(2)电荷从a移到c,电场力做的功W2。
一个正电荷在电场中只受到静电力F的作用,它在电场中由A点运动到B点时,静电力做了正功WAB。由动能定理可知,该电荷的动能增加了WAB。
从能量转化的角度思考,物体动能增加了,意味着另外一种形式的能量减少了。类比重力做功与重力势能的关系,这是一种什么形式的能量呢?
电荷只受静电力作用,只有静电力做功,故这种能量变化与静电力做功有关,静电力做功与重力做功特点相似:做功与路径无关,那么这种能就是势能的一种。
电势能Ep
1.概念:电荷在电场中具有的势能,这种势能称为电势能。用Ep表示。
2.大小:电荷在电场中某点的电势能,等于电荷从该点移动到零电势能点静电力所做的功。
3.电势能与静电力做功的关系:静电力做的功等于电势能的减小量,即WAB=EpA-EpB=-ΔEp。
4.电势能的相对性:选择不同的零电势能点,电荷在电场中同一点的电势能的值是不同(填“相同”或“不同”)的。
5.电势能为标量,正负值表示电势能的大小。
(1)分析正电荷只在静电力作用下从A→B运动(图甲)和从B→A运动时(图乙)静电力做功情况、动能和电势能的变化.
从A→B静电力做正功,动能增加,电势能减少
从B→A静电力做负功,动能减少,电势能增加
A
B
qE
WAB=EpA-EpB=EpA - 0
EpA=WAB
思考与讨论
mg
A
B
A
B
qE
(2)如果规定B点为零势能位置,若电荷从A移动至B静电力对电荷做功为WAB,则电荷在A点电势能是多少?
2.(多选)如图所示,在正点电荷产生的电场中的一条电场线上依次有A、B、C三点,分别把带电荷量为+q和-q的试探点电荷依次放在这三个点上,关于它们所具有的电势能,下列说法中正确的是
A.放上+q的试探点电荷时,试探点电荷在各点的电势能大小关系为EpA>EpB>EpC
B.放上+q的试探点电荷时,试探点电荷在各点的电势能大小关系为EpA<EpB<EpC
C.放上-q的试探点电荷时,试探点电荷在各点的电势能大小关系为EpA>EpB>EpC
D.放上-q的试探点电荷时,试探点电荷在各点的电势能大小关系为EpA<EpB<EpC
√
√
电势能大小的判断
1.做功判断法:无论正、负电荷,静电力做正功,电荷的电势能减小;静电力做负功,电荷的电势能增大。
2.能量守恒判断法:只有静电力做功时,电荷只有动能和电势能相互转化,总能量不变。因此,可由动能的变化确定电势能的变化。即只有静电力做功时,动能减少多少,电势能就增加多少;反之,动能增加多少,电势能就减少多少。
3.电场线法:(1)正电荷顺着电场线的方向移动时电势能逐渐减小,逆着电场线的方向移动时电势能逐渐增大;(2)负电荷顺着电场线的方向移动时电势能逐渐增大,逆着电场线的方向移动时电势能逐渐减小。
3.将带电荷量为6×10-6 C的负电荷从电场中的A点移到B点,克服静电力做了3×10-5 J的功,再从B移到C,静电力做了1.2×10-5 J的功,则:
(1)电荷从A移到C的整个过程中电势能改变了多少?
答案 (1)电势能增加了1.8×10-5 J。
(2) EpB=3×10-5 J,EpC=1.8×10-5 J。
(2)如果规定A点的电势能为零,则该电荷在B点和C点的电势能分别为多少?
(3)如果规定B点的电势能为零,则该电荷在A点和C点的电势能分别为多少?
静电力做功与电势能
静电力做功
电势能
特点:只与初末位置有关与路径无关
计算方法:W=qEdcos θ (θ为力与位移之间的夹角)
定义:电荷在电场中具有的势能
静电力做功与电势能变化的关系: WAB =EpA-EpB
电场力做正功,电势能减小
同课章节目录
- 第1章 静电力与电场强度
- 第1节 静电的产生及其微观解释
- 第2节 库仑定律
- 第3节 电场与电场强度
- 第4节 点电荷的电场 匀强电场
- 第5节 静电的利用与防护
- 第2章 电势能与电势差
- 第1节 静电力做功与电势能
- 第2节 电势与等势面
- 第3节 电势差与电场强度的关系
- 第4节 带电粒子在电场中的运动
- 第5节 科学探究:电容器
- 第3章 恒定电流
- 第1节 电流
- 第2节 电阻
- 第3节 电功与电热
- 第4节 串联电路和并联电路
- 第5节 科学测量:长度的测量及测量工具的选用
- 第6节 科学测量:金属丝的电阻率
- 第4章 闭合电路欧姆定律与科学用电
- 第1节 闭合电路欧姆定律
- 第2节 科学测量:电源的电动势和内阻
- 第3节 科学测量:用多用电表测量电学量
- 第4节 科学用电
- 第5章 初识电磁场与电磁波
- 第1节 磁场及其描述
- 第2节 电磁感应现象及其应用
- 第3节 初识电磁波及其应用
- 第4节 初识光量子与量子世界
- 第6章 能源与可持续发展
- 第1节 能量的多种形式
- 第2节 能量的转化与守恒
- 第3节 珍惜大自然
