江苏省苏州市星海实验中学2023-2024学年八年级上学期十月练习数学试卷(PDF版无答案)
文档属性
| 名称 | 江苏省苏州市星海实验中学2023-2024学年八年级上学期十月练习数学试卷(PDF版无答案) |
|
|
| 格式 | |||
| 文件大小 | 202.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-13 00:00:00 | ||
图片预览


文档简介
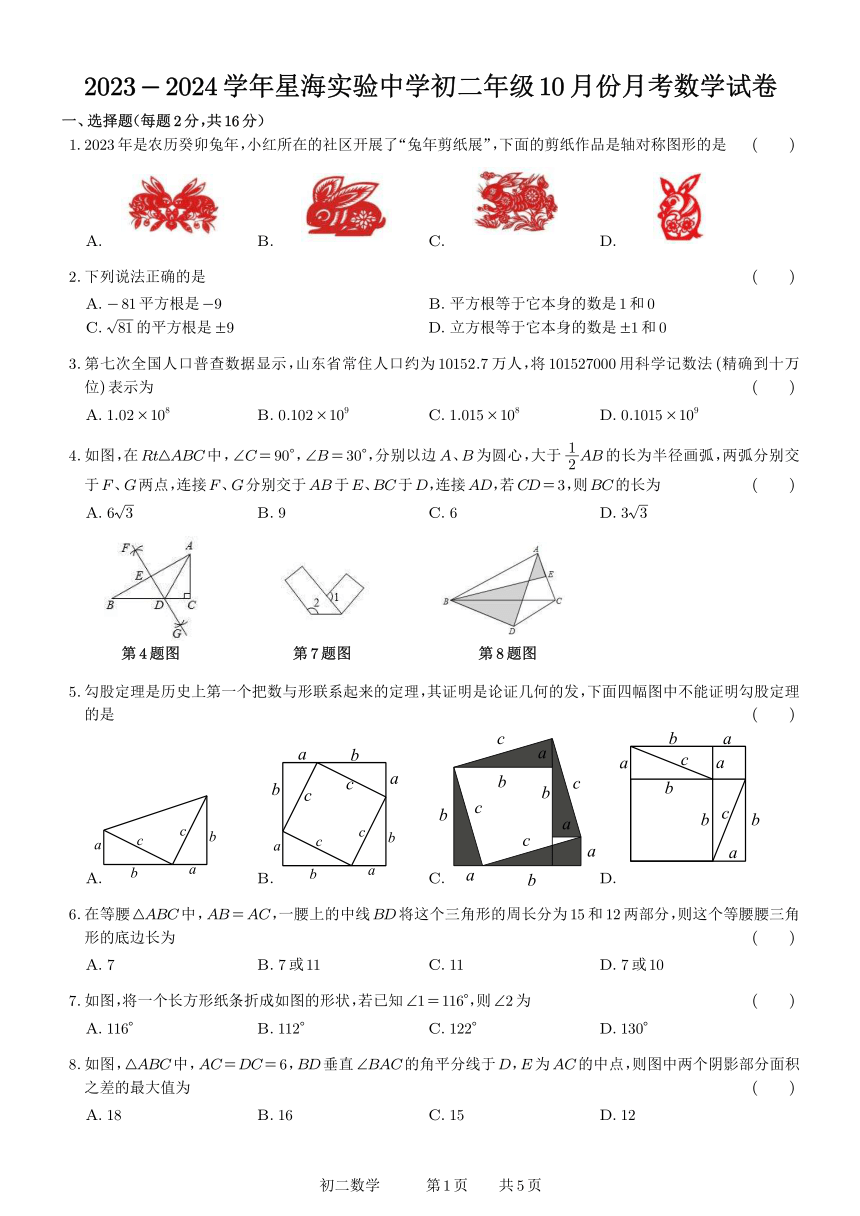
2023- 2024学年星海实验中学初二年级 10月份月考数学试卷
一、选择题(每题 2分,共 16分)
1. 2023年是农历癸卯兔年,小红所在的社区开展了“兔年剪纸展”,下面的剪纸作品是轴对称图形的是 ( )
A. B. C. D.
2.下列说法正确的是 ( )
A. - 81平方根是-9 B.平方根等于它本身的数是 1和 0
C. 81的平方根是±9 D.立方根等于它本身的数是±1和 0
3.第七次全国人口普查数据显示,山东省常住人口约为 10152.7万人,将 101527000用科学记数法 (精确到十万
位)表示为 ( )
A. 1.02× 108 B. 0.102× 109 C. 1.015× 108 D. 0.1015× 109
4.如图,在Rt△ABC中,∠C= 90° 1,∠B= 30°,分别以边A、B为圆心,大于 2 AB的长为半径画弧,两弧分别交
于F、G两点,连接F、G分别交于AB于E、BC于D,连接AD,若CD= 3,则BC的长为 ( )
A. 6 3 B. 9 C. 6 D. 3 3
第 4题图 第 7题图 第 8题图
5.勾股定理是历史上第一个把数与形联系起来的定理,其证明是论证几何的发,下面四幅图中不能证明勾股定理
的是 ( )
c b a
a b a a c a
b a b cc c b b
b c a b c b
c ca b a c
c b c a a
A. b a B. b a C. a b D.
6.在等腰△ABC中,AB=AC,一腰上的中线BD将这个三角形的周长分为 15和 12两部分,则这个等腰腰三角
形的底边长为 ( )
A. 7 B. 7或 11 C. 11 D. 7或 10
7.如图,将一个长方形纸条折成如图的形状,若已知∠1= 116°,则∠2为 ( )
A. 116° B. 112° C. 122° D. 130°
8.如图,△ABC中,AC=DC= 6,BD垂直∠BAC的角平分线于D,E为AC的中点,则图中两个阴影部分面积
之差的最大值为 ( )
A. 18 B. 16 C. 15 D. 12
初二数学 第 1页 共 5页
{#{QQABCQSAoggAQAJAAAgCQw2QCACQkAACCIoOhAAEMAIAgBNABAA=}#}
二、填空题 (每题 3分,共 24分)
9.一个正数 a的两个平方根是 2b- 1和 b+ 4,则 a为 .
10.如图所示的网格是正方形网格,各个顶点均为格点,则∠1+∠2= .
11.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个
全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为 a,较短直角边长为 b,
若 (a+ b)2= 21,小正方形的面积为 5,则大正方形的面积为 .
12.如图,数轴上点C、D分别表示 1、-1,BC垂直于数轴,且长为 1,以D为圆心、BD为半径作弧交数轴于点A,
则点A表示的实数是 .
13.如图 4× 5的方格纸中,在除阴影之外的方格中任意选择一个涂黑,与图中阴影部分构成轴对称图形的涂法有
种.
14.如图,把一张长方形纸片ABCD沿 EF折叠,点C与A重合,点D落在点G处.若长方形的长BC为 8,宽AB
为 4,则阴影部分的面积为 .
B
D
A
-2 -1 0 C1 2
10 (第 11题图) (第 12题图)
(第 13题图)
(第 题图)
15.如图,已知:四边形ABCD中,对角线BD平分∠ABC,∠DCB= 117°, ∠ABC= 50°,∠BAD+∠CAD= 180°,
那么∠DAC的度数为 度.
16.如图,等边△ABC中,AB= 2,点 E为高AD上的一动点,以 BE为边作等边△BEF ,连接DF ,CF ,则 FB+
FD的最小值为 .
第 14题图 第 15题图 第 16题图
三、解答题 (共 60分)
17. (6分)计算:
(1) (-1)2023- 36 ÷ 2 14 ÷ 3 27+ - 1
-2
2 (2) (- 6 )
2+ |2- 5 | + (-3)2
初二数学 第 2页 共 5页
{#{QQABCQSAoggAQAJAAAgCQw2QCACQkAACCIoOhAAEMAIAgBNABAA=}#}
18. (6分)求下面各式中的 x的值;
(1)5x2= 125; (2)2(x- 1)3+ 128= 0.
19. (4分)已知 5a+ 2的立方根是 3,4a+ b的算术平方根是 4,c是 51的整数部分.求 2a- 2b+ c的平方根.
20. (4分)如图,在边长为 1的小正方形方格纸中,有一个以格点为顶点的△ABC.
(1)利用网格线画△A′B′C ,使它与△ABC关于直线 l对称.
(2)在直线 l上作点P,使AP+CP的值最小,此时∠APC= .
(3)在直线 l上找一点Q,使点Q到AB、BC两边的距离相等.
A
B
C
21. (4分)如图,已知四边形ABCD.请用无刻度直尺和圆规,完成下列作图 (不要求写作法,保留作图痕迹):
(1)在线段AC上找一点M,使得BM=CM,请在图①中作出点M :
(2)若AB与CD不平行,且AB=CD,请在线段AC上找一点N,使得△ABN和△CDN的面积相等,请在图②
中作出点N .
D D
A A
B C B
图① 图②
初二数学 第 3页 共 5页
{#{QQABCQSAoggAQAJAAAgCQw2QCACQkAACCIoOhAAEMAIAgBNABAA=}#}
22. (4分)明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词,翻译为:如图秋千细索
OA悬挂于O点,静止时竖直下垂,A点为路板位置,踏板离地高度为一尺 (AC= 1尺).将它往前推进一些
(EB⊥OC于点 E,且 EB= 10尺),踏板升高到点 B位置,此时路板离地五尺 (BD= CE= 5尺),求秋千绳
(OA或OB)的长度.
O
E
A B
C D
23. (6分)如图,在△ABC中,AD是BC边上的高,CE是AB边上的中线,DG⊥CE于G,CD=AE.
(1)求证:CG=EG.
(2)已知BC= 13,CD= 5,连结ED,求△EDC的面积.
A
E
G
B D C
24. (6分)如图,点D是△ABC中,∠BAC的平分线和边BC的垂直平分线DE的交点,DG⊥AB于点G,DH⊥
AC交AC的延长线于点H.
(1)求证:BG=CH ;
(2)若AB= 12,AC= 8,求BG的长.
A
C
G E
H
B D
初二数学 第 4页 共 5页
{#{QQABCQSAoggAQAJAAAgCQw2QCACQkAACCIoOhAAEMAIAgBNABAA=}#}
25. (10分)定义:如果 1条线段将一个三角形分割成 2个等腰三角形,我们把这条线段叫做这个三角形的“双等腰
线”.如果 2条线段将一个三角形分成 3个等腰三角形,我们把这 2条线段叫做这个三角形的“三等腰线”“.
如图 1,DE是△ABD的”双等腰线“,AD、BE是△ABC的“三等腰线”.
(1)请在下图中,作出△ABC的“双等腰线”,并直接写出图中相等的线段。
①∠C= 90° ②∠B= 70°,∠A= 35° ③∠B= 81°,∠C= 27°
(2)如果一个等腰三角形有“双等腰线”,那么它的底角度数是 .
(3)如图,已知△ABC中,∠ACB= 90°,∠A= 30°,点O是AB的中点,过点C作∠BCD= 40°,交AB的延长线
于点D,CD边上的一点E恰好在OD的垂直平分线上,求证:线段CO、OE是△ACD的“三等腰线”:
26. (10分)如图,已知△ABC中,AC= 6cm,BC= 8cm,AB= 10cm,动点P从点C出发,沿着△ABC的三条边
逆时针走一圈回到C点,速度为 2cm/s,设运动时间为秒.
(1)t为何值时,AP平分∠CAB?
(2)求当 t为何值时,△ACP为等腰三角形?
(3)若P出发时,同时另有一点Q,从点C开始,按顺时针走方向运动,且速度为每秒 1cm.当P、Q中有一点到
达终点时,另一点也停止运动.是否存在某一时刻,直线PQ将△ABC的周长分成相等的两部分?若存在,求 t
的值,若不存在,说明理由.
初二数学 第 5页 共 5页
{#{QQABCQSAoggAQAJAAAgCQw2QCACQkAACCIoOhAAEMAIAgBNABAA=}#}
一、选择题(每题 2分,共 16分)
1. 2023年是农历癸卯兔年,小红所在的社区开展了“兔年剪纸展”,下面的剪纸作品是轴对称图形的是 ( )
A. B. C. D.
2.下列说法正确的是 ( )
A. - 81平方根是-9 B.平方根等于它本身的数是 1和 0
C. 81的平方根是±9 D.立方根等于它本身的数是±1和 0
3.第七次全国人口普查数据显示,山东省常住人口约为 10152.7万人,将 101527000用科学记数法 (精确到十万
位)表示为 ( )
A. 1.02× 108 B. 0.102× 109 C. 1.015× 108 D. 0.1015× 109
4.如图,在Rt△ABC中,∠C= 90° 1,∠B= 30°,分别以边A、B为圆心,大于 2 AB的长为半径画弧,两弧分别交
于F、G两点,连接F、G分别交于AB于E、BC于D,连接AD,若CD= 3,则BC的长为 ( )
A. 6 3 B. 9 C. 6 D. 3 3
第 4题图 第 7题图 第 8题图
5.勾股定理是历史上第一个把数与形联系起来的定理,其证明是论证几何的发,下面四幅图中不能证明勾股定理
的是 ( )
c b a
a b a a c a
b a b cc c b b
b c a b c b
c ca b a c
c b c a a
A. b a B. b a C. a b D.
6.在等腰△ABC中,AB=AC,一腰上的中线BD将这个三角形的周长分为 15和 12两部分,则这个等腰腰三角
形的底边长为 ( )
A. 7 B. 7或 11 C. 11 D. 7或 10
7.如图,将一个长方形纸条折成如图的形状,若已知∠1= 116°,则∠2为 ( )
A. 116° B. 112° C. 122° D. 130°
8.如图,△ABC中,AC=DC= 6,BD垂直∠BAC的角平分线于D,E为AC的中点,则图中两个阴影部分面积
之差的最大值为 ( )
A. 18 B. 16 C. 15 D. 12
初二数学 第 1页 共 5页
{#{QQABCQSAoggAQAJAAAgCQw2QCACQkAACCIoOhAAEMAIAgBNABAA=}#}
二、填空题 (每题 3分,共 24分)
9.一个正数 a的两个平方根是 2b- 1和 b+ 4,则 a为 .
10.如图所示的网格是正方形网格,各个顶点均为格点,则∠1+∠2= .
11.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个
全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为 a,较短直角边长为 b,
若 (a+ b)2= 21,小正方形的面积为 5,则大正方形的面积为 .
12.如图,数轴上点C、D分别表示 1、-1,BC垂直于数轴,且长为 1,以D为圆心、BD为半径作弧交数轴于点A,
则点A表示的实数是 .
13.如图 4× 5的方格纸中,在除阴影之外的方格中任意选择一个涂黑,与图中阴影部分构成轴对称图形的涂法有
种.
14.如图,把一张长方形纸片ABCD沿 EF折叠,点C与A重合,点D落在点G处.若长方形的长BC为 8,宽AB
为 4,则阴影部分的面积为 .
B
D
A
-2 -1 0 C1 2
10 (第 11题图) (第 12题图)
(第 13题图)
(第 题图)
15.如图,已知:四边形ABCD中,对角线BD平分∠ABC,∠DCB= 117°, ∠ABC= 50°,∠BAD+∠CAD= 180°,
那么∠DAC的度数为 度.
16.如图,等边△ABC中,AB= 2,点 E为高AD上的一动点,以 BE为边作等边△BEF ,连接DF ,CF ,则 FB+
FD的最小值为 .
第 14题图 第 15题图 第 16题图
三、解答题 (共 60分)
17. (6分)计算:
(1) (-1)2023- 36 ÷ 2 14 ÷ 3 27+ - 1
-2
2 (2) (- 6 )
2+ |2- 5 | + (-3)2
初二数学 第 2页 共 5页
{#{QQABCQSAoggAQAJAAAgCQw2QCACQkAACCIoOhAAEMAIAgBNABAA=}#}
18. (6分)求下面各式中的 x的值;
(1)5x2= 125; (2)2(x- 1)3+ 128= 0.
19. (4分)已知 5a+ 2的立方根是 3,4a+ b的算术平方根是 4,c是 51的整数部分.求 2a- 2b+ c的平方根.
20. (4分)如图,在边长为 1的小正方形方格纸中,有一个以格点为顶点的△ABC.
(1)利用网格线画△A′B′C ,使它与△ABC关于直线 l对称.
(2)在直线 l上作点P,使AP+CP的值最小,此时∠APC= .
(3)在直线 l上找一点Q,使点Q到AB、BC两边的距离相等.
A
B
C
21. (4分)如图,已知四边形ABCD.请用无刻度直尺和圆规,完成下列作图 (不要求写作法,保留作图痕迹):
(1)在线段AC上找一点M,使得BM=CM,请在图①中作出点M :
(2)若AB与CD不平行,且AB=CD,请在线段AC上找一点N,使得△ABN和△CDN的面积相等,请在图②
中作出点N .
D D
A A
B C B
图① 图②
初二数学 第 3页 共 5页
{#{QQABCQSAoggAQAJAAAgCQw2QCACQkAACCIoOhAAEMAIAgBNABAA=}#}
22. (4分)明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词,翻译为:如图秋千细索
OA悬挂于O点,静止时竖直下垂,A点为路板位置,踏板离地高度为一尺 (AC= 1尺).将它往前推进一些
(EB⊥OC于点 E,且 EB= 10尺),踏板升高到点 B位置,此时路板离地五尺 (BD= CE= 5尺),求秋千绳
(OA或OB)的长度.
O
E
A B
C D
23. (6分)如图,在△ABC中,AD是BC边上的高,CE是AB边上的中线,DG⊥CE于G,CD=AE.
(1)求证:CG=EG.
(2)已知BC= 13,CD= 5,连结ED,求△EDC的面积.
A
E
G
B D C
24. (6分)如图,点D是△ABC中,∠BAC的平分线和边BC的垂直平分线DE的交点,DG⊥AB于点G,DH⊥
AC交AC的延长线于点H.
(1)求证:BG=CH ;
(2)若AB= 12,AC= 8,求BG的长.
A
C
G E
H
B D
初二数学 第 4页 共 5页
{#{QQABCQSAoggAQAJAAAgCQw2QCACQkAACCIoOhAAEMAIAgBNABAA=}#}
25. (10分)定义:如果 1条线段将一个三角形分割成 2个等腰三角形,我们把这条线段叫做这个三角形的“双等腰
线”.如果 2条线段将一个三角形分成 3个等腰三角形,我们把这 2条线段叫做这个三角形的“三等腰线”“.
如图 1,DE是△ABD的”双等腰线“,AD、BE是△ABC的“三等腰线”.
(1)请在下图中,作出△ABC的“双等腰线”,并直接写出图中相等的线段。
①∠C= 90° ②∠B= 70°,∠A= 35° ③∠B= 81°,∠C= 27°
(2)如果一个等腰三角形有“双等腰线”,那么它的底角度数是 .
(3)如图,已知△ABC中,∠ACB= 90°,∠A= 30°,点O是AB的中点,过点C作∠BCD= 40°,交AB的延长线
于点D,CD边上的一点E恰好在OD的垂直平分线上,求证:线段CO、OE是△ACD的“三等腰线”:
26. (10分)如图,已知△ABC中,AC= 6cm,BC= 8cm,AB= 10cm,动点P从点C出发,沿着△ABC的三条边
逆时针走一圈回到C点,速度为 2cm/s,设运动时间为秒.
(1)t为何值时,AP平分∠CAB?
(2)求当 t为何值时,△ACP为等腰三角形?
(3)若P出发时,同时另有一点Q,从点C开始,按顺时针走方向运动,且速度为每秒 1cm.当P、Q中有一点到
达终点时,另一点也停止运动.是否存在某一时刻,直线PQ将△ABC的周长分成相等的两部分?若存在,求 t
的值,若不存在,说明理由.
初二数学 第 5页 共 5页
{#{QQABCQSAoggAQAJAAAgCQw2QCACQkAACCIoOhAAEMAIAgBNABAA=}#}
同课章节目录
