第24章 圆单元测试卷（含答案）

第24章圆单元测试卷
(满分100分)
一、选择题(本大题共10小题，每小题3分，共30分)
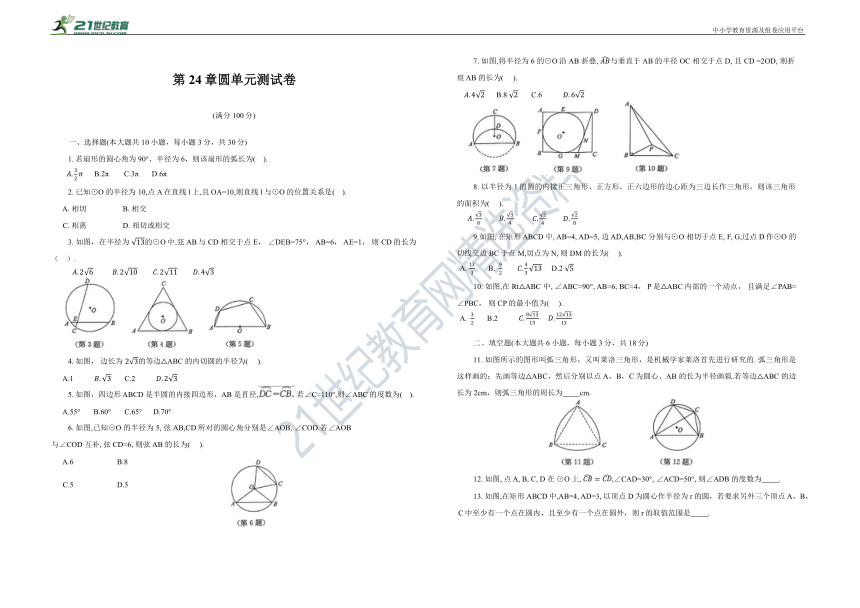
1. 若扇形的圆心角为 90°，半径为 6，则该扇形的弧长为( ).
B.2π C.3π D.6π
2. 已知⊙O 的半径为 10,点A 在直线l上,且OA=10,则直线l与⊙O 的位置关系是( ).
A. 相切 B. 相交
C. 相离 D. 相切或相交
3. 如图，在半径为 的⊙O中,弦 AB与CD 相交于点E， ∠DEB=75°， AB=6， AE=1， 则CD的长为（ ）.
4. 如图， 边长为 的等边△ABC 的内切圆的半径为( ).
A.1 C.2
5. 如图，四边形 ABCD 是半圆的内接四边形，AB 是直径, 若∠C=110°,则∠ABC的度数为( ).
A.55° B.60° C.65° D.70°
6. 如图,已知⊙O 的半径为 5, 弦AB,CD所对的圆心角分别是∠AOB, ∠COD.若∠AOB 与∠COD 互补, 弦 CD=6, 则弦AB 的长为( ).
A.6 B.8
C.5 D.5
7. 如图,将半径为6 的⊙O沿AB 折叠, 与垂直于AB的半径 OC 相交于点 D, 且 CD =2OD, 则折痕 AB 的长为( ).
B.8 C.6
8. 以半径为 1的圆的内接正三角形、正方形、正六边形的边心距为三边长作三角形，则该三角形的面积为( ).
9.如图, 在矩形 ABCD中, AB=4, AD=5, 边 AD,AB,BC 分别与⊙O 相切于点E, F, G,过点 D作⊙O 的切线交边 BC于点M,切点为 N, 则 DM的长为( ).
A. B. D.2
10. 如图,在Rt△ABC 中, ∠ABC=90°, AB=6, BC=4， P是△ABC内部的一个动点， 且满足∠PAB=∠PBC， 则CP 的最小值为( ).
A. B.2
二、填空题(本大题共6小题，每小题3分，共18分)
11. 如图所示的图形叫弧三角形，又叫莱洛三角形，是机械学家莱洛首先进行研究的. 弧三角形是这样画的：先画等边△ABC，然后分别以点A，B，C为圆心、AB 的长为半径画弧.若等边△ABC 的边长为2cm，则弧三角形的周长为 cm.
12. 如图, 点 A, B, C, D 在 ⊙O 上, ∠CAD=30°, ∠ACD=50°, 则∠ADB 的度数为 .
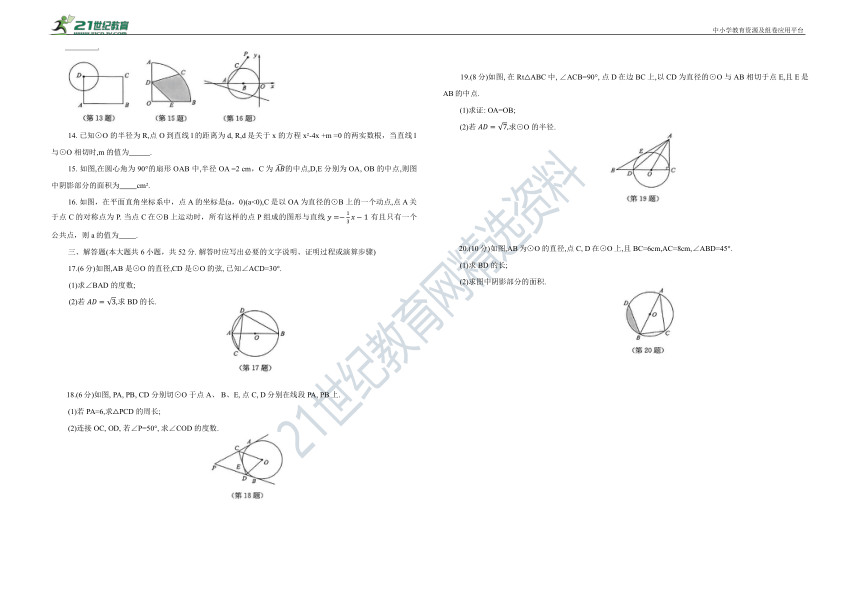
13. 如图,在矩形ABCD中,AB=4, AD=3, 以顶点D为圆心作半径为r的圆，若要求另外三个顶点A，B，C中至少有一个点在圆内，且至少有一个点在圆外，则r的取值范围是 .
14. 已知⊙O 的半径为R,点O到直线l的距离为d, R,d是关于x 的方程x -4x +m =0的两实数根，当直线l与⊙O 相切时,m 的值为 .
15. 如图,在圆心角为 90°的扇形 OAB 中,半径 OA =2 cm，C为 的中点,D,E分别为OA, OB 的中点,则图中阴影部分的面积为 cm .
16. 如图，在平面直角坐标系中，点A 的坐标是(a，0)(a<0),C是以OA 为直径的⊙B 上的一个动点,点 A 关于点C的对称点为 P. 当点C在⊙B上运动时，所有这样的点 P组成的图形与直线 有且只有一个公共点，则a的值为 .
三、解答题(本大题共6小题，共52分. 解答时应写出必要的文字说明、证明过程或演算步骤)
17.(6分)如图,AB 是⊙O 的直径,CD 是⊙O 的弦, 已知∠ACD=30°.
(1)求∠BAD 的度数;
(2)若 求BD 的长.
18.(6分)如图, PA, PB, CD 分别切⊙O 于点A、 B、E, 点C, D分别在线段 PA, PB上.
(1)若 PA=6,求△PCD 的周长;
(2)连接OC, OD, 若∠P=50°, 求∠COD 的度数.
19.(8分)如图, 在 Rt△ABC中, ∠ACB=90°, 点D在边BC上,以CD为直径的⊙O 与AB 相切于点E,且E是AB的中点.
(1)求证: OA=OB;
(2)若 求⊙O 的半径.
20.(10分)如图,AB为⊙O 的直径,点C, D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.
(1)求 BD 的长;
(2)求图中阴影部分的面积.
21.(10分)如图,四边形 ABCD 为菱形, 以边 AD为直径作⊙O交边AB 于点 F,连接 DB 交⊙O 于点 H, E 是边 BC上的一点， 且BE=BF.
(1)求证: DE 是⊙O 的切线;
(2)若 求⊙O 的半径.
22.(12分)如图, ⊙O 的半径为 l, 点A, P, B, C在⊙O上, 且∠APC=∠CPB=60°.
(1)判断△ABC 的形状;
(2)试探究 PA，PB，PC之间的数量关系，并证明你的结论；
(3)当点 P 位于 的什么位置时，四边形 APBC 的面积最大 求出最大面积.
中小学教育资源及组卷应用平台
单元点评四
1. C 2. D 3. C 4. A 5. A 6. B 7. B 8. D 9. A 10. B11.2π 12.70° 13.317.(1)∵AB 是⊙O 的直径,
∴∠ADB=90°.
∵∠B=∠ACD=30°,
∴∠BAD=90°-∠B=90°-30°=60°.
(2)在 Rt△ADB 中,AB=2AD,
18. (1)∵PA,PB切⊙O 于点A, B,CD切⊙O 于点E,
∴PA=PB=6, ED=BD, CE=AC,
∴△PCD的周长=PD+DE+PC+CE=2PA=12.
(2)连接OE,OA, OB,如图.
由切线的性质得OA⊥PA,OB⊥PB,OE⊥CD,
∴∠OAC=∠OEC=∠OED=∠OBD=90°,
∴∠AOB+∠P=180°,
∴∠AOB=180°-∠P=130°.
由切线长定理得∠AOC=∠EOC,∠EOD=∠BOD,
19.(1)连接OE, 如图.
∵以CD为直径的⊙O 与直线AB 相切于点E，
∴OE⊥AB.
∵E是AB的中点,
∴OE 垂直平分AB,
∴OA=OB.
(2)设⊙O的半径为r.
∵OE⊥AB,OC⊥AC, OE=OC,
∴AO平分∠BAC,
∴∠OAC=∠OAB.
∵OA=OB,
∴∠B=∠OAB,
∴∠OAC=∠B=∠OAB=30°.
在 Rt△OAC中,OC=r, AO=2r,
在 Rt△ACD 中,
解得r=±1(-1舍去),即⊙O 的半径为 1.
20.(1)连接OD,如图.
∵AB 为⊙O 的直径,
∴∠ACB=90°.
∵BC=6cm, AC=8cm,
∴AB=10 cm.
∴OB=5 cm.
∵OD=OB,
∴∠ODB=∠ABD=45°,
∴∠BOD=90°,
21. (1)如图①,连接 DF.
∵四边形 ABCD 为菱形,
∴AB=BC=CD=DA, AD∥BC,∠A=∠C.
∵BF=BE,
∴AB-BF=BC-BE, 即AF=CE,
∴△DAF≌△DCE(SAS),
∴∠DFA=∠DEC.
∵AD 是⊙O 的直径,
∴∠DFA =90°,
∴∠DEC=90°.
∵AD∥BC,
∴∠ADE=∠DEC=90°,
∴OD⊥DE.
∵OD 是⊙O 的半径,
∴DE 是⊙O 的切线.
(2)如图②,连接 AH.
∵AD 是⊙O 的直径,
∴∠AHD=∠DFA=90°,
∴∠DFB=90°.
∵AD=AB, DH= ,
∴DB=2DH=2 .
在 Rt△ADF 和 Rt△BDF 中,
∵DF =AD -AF , DF =BD -BF ,
∴AD -AF =DB -BF ,
∴AD -(AD-BF) =DB -BF ,
解得AD=5,
∴⊙O的半径为
22.(1)在⊙O 中, ∵∠BAC 与∠CPB 是 所对的圆周角，∠ABC与∠APC是 所对的圆周角，
∴∠BAC=∠CPB=60°, ∠ABC=∠APC=60°,
∴△ABC为等边三角形.
(2)CP=BP+AP.
证明: 在 PC上截取PD=AP,连接AD,如图①.
∵∠APC=60°,
∴△APD 是等边三角形,
∴AD=AP=PD, ∠ADP=60°,
∴∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB.
在△APB 和△ADC 中,
∴△APB≌△ADC(AAS),
∴BP=CD.
又∵PD=AP，
∴CP=BP+AP.
(3)当P为 的中点时， 四边形 APBC的面积最大.
如图②,过点 P 作PE⊥AB 于点E,过点C作CF⊥AB 于点F,连接AO.
当P为 的中点时， PE+CF=PC， PC为⊙O 的直径， 此时四边形 APBC 的面积最大.
∵△ABC为等边三角形,
∴CF 过点O, AF=BF, ∠BAO=30°.
在 Rt△AOF中，