专题1.11正方形的性质与判定 直通中考练习(含解析)2023-2024学年九年级数学上册北师大版专项讲练
文档属性
| 名称 | 专题1.11正方形的性质与判定 直通中考练习(含解析)2023-2024学年九年级数学上册北师大版专项讲练 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-12 00:00:00 | ||
图片预览



文档简介
专题1.11 正方形的性质与判定(直通中考)
【要点回顾】
一、正方形的性质
(1)四边都相等;(2)四个角都是直角;(3)对称线垂直平分且相等;(4)是轴对称图形,也是中心对称图形.
二、正方形的判定
(1)定义法:有一组邻边相等并且有一个内角是直角的平行四边形;
(2)判定定理1:对角线相等的菱形是正方形;
(3)判定定理2:对角线相互垂直的矩形是正方形;
(4)判定定理3:有一个内角是直角的菱形是正方形;
(5)判定定理4:有一组邻边相等的矩形是正方形.
一、单选题
(2023·四川自贡·统考中考真题)
1.如图,边长为的正方形两边与坐标轴正半轴重合,点的坐标是( )
A. B. C. D.
(2022·浙江嘉兴·统考中考真题)
2.“方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得到正方形,形成一个“方胜”图案,则点D,之间的距离为( )
A.1cm B.2cm C.(-1)cm D.(2-1)cm
(2023·四川广安·统考中考真题)
3.下列说法正确的是( )
A.三角形的一个外角等于两个内角的和
B.对角线相等且互相垂直的四边形是正方形
C.在一组数据11,9,7,8,6,8,12,8中,众数和中位数都是8
D.甲乙两组各10名同学参加“安全知识竞赛”,若两组同学的平均成绩相同,甲组的方差,乙组的方差,则甲组同学的成绩比乙组同学的成绩稳定
(2022·浙江绍兴·统考中考真题)
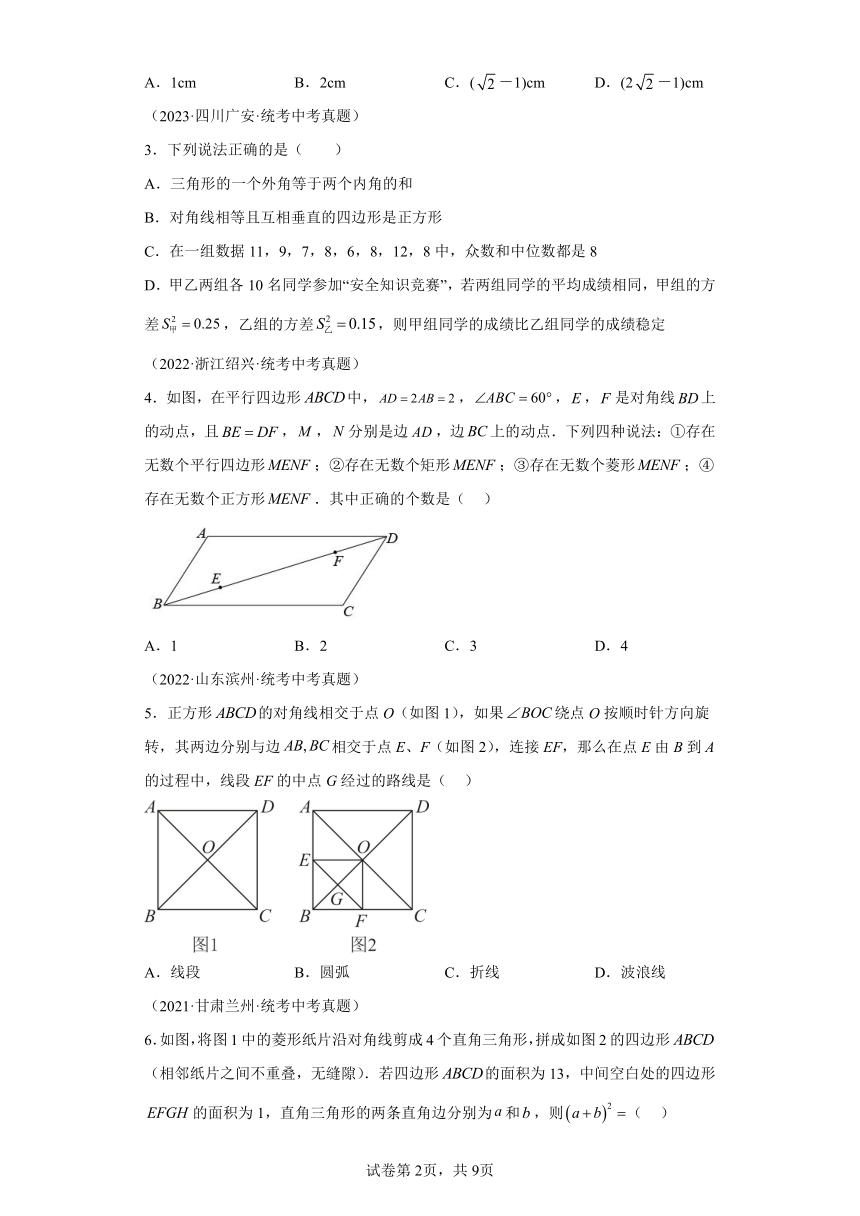
4.如图,在平行四边形中,,,,是对角线上的动点,且,,分别是边,边上的动点.下列四种说法:①存在无数个平行四边形;②存在无数个矩形;③存在无数个菱形;④存在无数个正方形.其中正确的个数是( )
A.1 B.2 C.3 D.4
(2022·山东滨州·统考中考真题)
5.正方形的对角线相交于点O(如图1),如果绕点O按顺时针方向旋转,其两边分别与边相交于点E、F(如图2),连接EF,那么在点E由B到A的过程中,线段EF的中点G经过的路线是( )
A.线段 B.圆弧 C.折线 D.波浪线
(2021·甘肃兰州·统考中考真题)
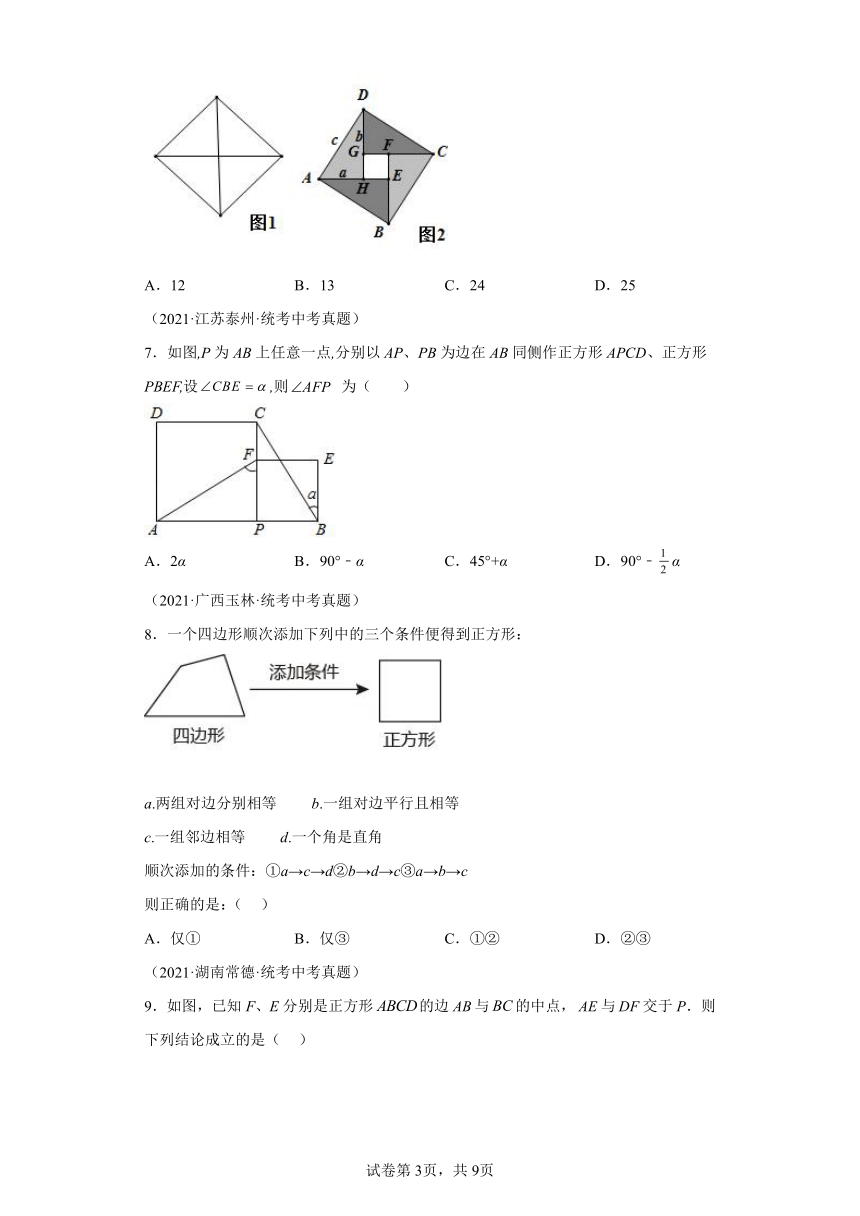
6.如图,将图1中的菱形纸片沿对角线剪成4个直角三角形,拼成如图2的四边形(相邻纸片之间不重叠,无缝隙).若四边形的面积为13,中间空白处的四边形的面积为1,直角三角形的两条直角边分别为和,则( )
A.12 B.13 C.24 D.25
(2021·江苏泰州·统考中考真题)
7.如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设,则 为( )
A.2α B.90°﹣α C.45°+α D.90°﹣α
(2021·广西玉林·统考中考真题)
8.一个四边形顺次添加下列中的三个条件便得到正方形:
a.两组对边分别相等 b.一组对边平行且相等
c.一组邻边相等 d.一个角是直角
顺次添加的条件:①a→c→d②b→d→c③a→b→c
则正确的是:( )
A.仅① B.仅③ C.①② D.②③
(2021·湖南常德·统考中考真题)
9.如图,已知F、E分别是正方形的边与的中点,与交于P.则下列结论成立的是( )
A. B. C. D.
(2021·重庆·统考中考真题)
10.如图,把含30°的直角三角板PMN放置在正方形ABCD中,,直角顶点P在正方形ABCD的对角线BD上,点M,N分别在AB和CD边上,MN与BD交于点O,且点O为MN的中点,则的度数为( )
A.60° B.65° C.75° D.80°
二、填空题
(2023·湖南·统考中考真题)
11.七巧板是我国民间广为流传的一种益智玩具,某同学用边长为的正方形纸板制作了一副七巧板(如图),由5个等腰直角三角形,1个正方形和1个平行四边形组成.则图中阴影部分的面积为 .
(2022·江苏常州·统考中考真题)
12.如图,将一个边长为的正方形活动框架(边框粗细忽略不计)扭动成四边形,对角线是两根橡皮筋,其拉伸长度达到时才会断裂.若,则橡皮筋 断裂(填“会”或“不会”,参考数据:).
(2022·江西·统考中考真题)
13.沐沐用七巧板拼了一个对角线长为2的正方形,再用这副七巧板拼成一个长方形(如图所示),则长方形的对角线长为 .
(2021·上海·统考中考真题)
14.定义:在平面内,一个点到图形的距离是这个点到这个图上所有点的最短距离,在平面内有一个正方形,边长为2,中心为O,在正方形外有一点,当正方形绕着点O旋转时,则点P到正方形的最短距离d的取值范围为 .
(2021·浙江金华·统考中考真题)
15.如图,在平面直角坐标系中,有一只用七巧板拼成的“猫”,三角形①的边BC及四边形②的边CD都在x轴上,“猫”耳尖E在y轴上.若“猫”尾巴尖A的横坐标是1,则“猫”爪尖F的坐标是 .
(2023·河南南阳·统考三模)
16.如图,在正方形中,,在等腰直角三角形中,,.边与在同一直线上..若正方形以的速度沿直线向右运动,经过 ,此三角形和正方形重叠部分的面积是.
(2023·贵州贵阳·校考一模)
17.如图,在正方形中,,点为上一动点,连接,以为边在上方作正方形.若点是的中点,且,则的长是 ;点从点到点的运动过程中,点所运动的路径长是 .
(2023·安徽宣城·校考三模)
18.在正方形中,将绕点B逆时针旋转得到,连接.
(1)当时, ;
(2)在上取点F,使,连接.若,当时,的最小值为 .
三、解答题
(2022·贵州遵义·统考中考真题)
19.将正方形和菱形按照如图所示摆放,顶点与顶点重合,菱形的对角线经过点,点,分别在,上.
(1)求证:;
(2)若,求的长.
(2023·湖北十堰·统考中考真题)
20.过正方形的顶点作直线,点关于直线的对称点为点,连接,直线交直线于点.
(1)如图1,若,则___________;
(2)如图1,请探究线段,,之间的数量关系,并证明你的结论;
(3)在绕点转动的过程中,设,请直接用含的式子表示的长.
(2022·新疆·统考中考真题)
21.如图,在巾,,点O为BC的中点,点D是线段OC上的动点(点D不与点O,C重合),将沿AD折叠得到,连接BE.
(1)当时,___________;
(2)探究与之间的数量关系,并给出证明;
(3)设,的面积为x,以AD为边长的正方形的面积为y,求y关于x的函数解析式.
(2022·江苏常州·统考中考真题)
22.在四边形中,是边上的一点.若,则点叫做该四边形的“等形点”.
(1)正方形_______“等形点”(填“存在”或“不存在”);
(2)如图,在四边形中,边上的点是四边形的“等形点”.已知,,,连接,求的长;
(3)在四边形中,EH//FG.若边上的点是四边形的“等形点”,求的值.
(2022·辽宁朝阳·统考中考真题)
23.【思维探究】如图1,在四边形ABCD中,∠BAD=60°,∠BCD=120°,AB=AD,连接AC.求证:BC+CD=AC.
(1)小明的思路是:延长CD到点E,使DE=BC,连接AE.根据∠BAD+∠BCD=180°,推得∠B+∠ADC=180°,从而得到∠B=∠ADE,然后证明ADE≌ABC,从而可证BC+CD=AC,请你帮助小明写出完整的证明过程.
(2)【思维延伸】如图2,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,连接AC,猜想BC,CD,AC之间的数量关系,并说明理由.
(3)【思维拓展】在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD=,AC与BD相交于点O.若四边形ABCD中有一个内角是75°,请直接写出线段OD的长.
(2023·湖南·统考中考真题)
24.问题情境:小红同学在学习了正方形的知识后,进一步进行以下探究活动:在正方形的边上任意取一点G,以为边长向外作正方形,将正方形绕点B顺时针旋转.
特例感知:
(1)当在上时,连接相交于点P,小红发现点P恰为的中点,如图①.针对小红发现的结论,请给出证明;
(2)小红继续连接,并延长与相交,发现交点恰好也是中点P,如图②,根据小红发现的结论,请判断的形状,并说明理由;
规律探究:
(3)如图③,将正方形绕点B顺时针旋转,连接,点P是中点,连接,,,的形状是否发生改变?请说明理由.
试卷第8页,共9页
试卷第1页,共9页
参考答案:
1.C
【分析】根据正方形的性质,结合坐标的意义即可求解.
【详解】解:∵边长为的正方形两边与坐标轴正半轴重合,
∴
∴,
故选:C.
【点睛】本题考查了坐标与图形,熟练掌握正方形的性质,数形结合是解题的关键.
2.D
【分析】先求出BD,再根据平移性质求得=1cm,然后由求解即可.
【详解】解:由题意,BD=cm,
由平移性质得=1cm,
∴点D,之间的距离为==()cm,
故选:D.
【点睛】本题考查平移性质、正方形的性质,熟练掌握平移性质是解答的关键.
3.C
【分析】根据三角形的外角定理,正方形的判定,众数和中位数的定义,方差的意义判断即可.
【详解】解:A.三角形的一个外角等于与它不相邻两个内角的和,故选项A错误;
B.要加上 “对角线互相平分”这个条件,故选项B错误;
C.这列数据从小到大排列为6,7,8,8,8,9,11,12,
8出现了3次,故众数是8,中位数是,
故选项C正确;
D.方差越小,数据越稳定,故选项D错误.
故选:C.
【点睛】本题考查了三角形的外角定理,正方形的判定,众数和中位数的定义,方差的意义等知识,本题的关键是熟练掌握这些知识点,并能灵活运用.
4.C
【分析】根据题意作出合适的辅助线,然后逐一分析即可.
【详解】
如图,连接AC、与BD交于点O,连接ME,MF,NF,EN,MN,
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
∵BE=DF
∴OE=OF
∵点E、F时BD上的点,
∴只要M,N过点O,
那么四边形MENF就是平行四边形
∴存在无数个平行四边形MENF,故①正确;
只要MN=EF,MN过点O,则四边形MENF是矩形,
∵点E、F是BD上的动点,
∴存在无数个矩形MENF,故②正确;
只要MN⊥EF,MN过点O,则四边形MENF是菱形;
∵点E、F是BD上的动点,
∴存在无数个菱形MENF,故③正确;
只要MN=EF,MN⊥EF,MN过点O,
则四边形MENF是正方形,
而符合要求的正方形只有一个,故④错误;
故选:C
【点睛】本题考查正方形的判定、菱形的判定、矩形的判定、平行四边形的判定、解答本题的关键时明确题意,作出合适的辅助线.
5.A
【分析】连接,根据题意可知则线段EF的中点G经过的路线是的线段垂直平分线的一段,即线段
【详解】连接,根据题意可知,
,
∴点G在线段OB的垂直平分线上.
则线段EF的中点G经过的路线是的线段垂直平分线的一段,即线段.
故选:A.
【点睛】本题考查了线段垂直平分线的判定,直角三角形斜边上的中线等于斜边的一半,正方形的性质,掌握以上知识是解题的关键.
6.D
【分析】根据菱形的性质可得对角线互相垂直平分,进而可得4个直角三角形全等,结合已知条件和勾股定理求得,进而根据面积差以及三角形面积公式求得,最后根据完全平方公式即可求得.
【详解】菱形的对角线互相垂直平分,
个直角三角形全等;
,,
,
四边形是正方形,又正方形的面积为13,
正方形的边长为,
根据勾股定理,则,
中间空白处的四边形的面积为1,
个直角三角形的面积为,
,
,
,
.
故选D.
【点睛】本题考查了正方形的性质与判定,菱形的性质,勾股定理,完全平方公式,求得是解题的关键.
7.B
【分析】根据题意可得 ,从而 即可.
【详解】∵四边形APCD和四边形PBEF是正方形,
∴AP=CP,PF=PB,,
∴,
∴∠AFP=∠CBP,
又∵ ,
∴,
故选:B.
【点睛】本题主要考查了正方形的性质,全等三角形的判定,熟练掌握正方形的性质,全等三角形的判定方法是解题的关键.
8.C
【分析】根据题意及正方形的判定定理可直接进行排除选项.
【详解】解:①由两组对边分别相等可得该四边形是平行四边形,添加一组邻边相等可得该四边形是菱形,再添加一个角是直角则可得该四边形是正方形;正确,故符合题意;
②由一组对边平行且相等可得该四边形是平行四边形,添加一个角是直角可得该四边形是矩形,再添加一组邻边相等则可得该四边形是正方形;正确,故符合题意;
③a、b都为平行四边形的判定定理,故不能判定该四边形是正方形,故错误,不符合题意;
∴正确的有①②;
故选C.
【点睛】本题主要考查正方形的判定,熟练掌握正方形的判定定理是解题的关键.
9.C
【分析】根据正方形的性质,全等三角形的判定和性质以及等腰三角形的性质逐一判断即可.
【详解】解:∵四边形ABCD是正方形,
∴AB=BC=CD=CA,∠ABC=∠BCD=∠CDA=∠DAB=90°,
∵已知F、E分别是正方形ABCD的边AB与BC的中点,
∴BE=BC=AB在△ABE和△DAF中,
,
∴△ABE≌△DAF(SAS),
∴∠BAE=∠ADF,
∵∠ADF+∠AFD=90°,
∴∠BAE+∠AFD =90°,
∴∠APF=90°,
∴∠EAF+∠AFD=90°,故C选项正确,符合题意;
连接FC,
同理可证得△CBF≌△DAF(SAS),
∴∠BCF=∠ADF,
∴∠BCD-∠BCF=∠ADC-∠ADF,即90°-∠BCF=90°-∠ADF,
∴∠PDC=∠FCD>∠PCD,
∴PC>PD,故B选项错误,不符合题意;
∵AD>PD,
∴CD>PD,
∴∠DPC>∠DCP,
∴90°-∠DPC<90°-∠DCP,
∴∠CPE<∠PCE,
∴PE> CE,故D选项错误,不符合题意;
故选:C.
【点睛】本题考查了正方形的性质,全等三角形的判定与性质,等腰三角形的性质等知识.此题综合性很强,解题的关键是注意数形结合思想的应用.
10.C
【分析】根据斜边中线等于斜边一半,求出∠MPO=30°,再求出∠MOB和∠OMB的度数,即可求出的度数.
【详解】解:∵四边形ABCD是正方形中,
∴∠MBO=∠NDO=45°,
∵点O为MN的中点
∴OM=ON,
∵∠MPN=90°,
∴OM=OP,
∴∠PMN=∠MPO=30°,
∴∠MOB=∠MPO+∠PMN =60°,
∴∠BMO=180°-60°-45°=75°,
,
故选:C.
【点睛】本题考查了正方形的性质和直角三角形的性质、等腰三角形的性质,解题关键是熟练运用相关性质,根据角的关系进行计算.
11.
【分析】根据正方形的性质,以及七巧板的特点,求得的长,即可求解.
【详解】解:如图所示,
依题意,,
∴图中阴影部分的面积为
故答案为:.
【点睛】本题考查了正方形的性质,勾股定理,七巧板,熟练掌握以上知识是解题的关键.
12.不会
【分析】设扭动后对角线的交点为,根据正方形的性质,得出扭动后的四边形为菱形,利用菱形的性质及条件,得出为等边三角形,利用勾股定理算出,从而得到,再比较即可判断.
【详解】解:设扭动后对角线的交点为,如下图:
,
根据正方形的性质得,
得出扭动后的四边形四边相等为菱形,
cm,
为等边三角形,
cm,
cm,
cm,
根据菱形的对角线的性质:(cm),
,
不会断裂,
故答案为:不会.
【点睛】本题考查了正方形的性质、菱形的判定及性质、等边三角形、勾股定理,解题的关键是要掌握菱形的判定及性质.
13.
【分析】根据图形可得长方形的长是正方形的对角线为2,长方形的宽是正方形对角线的一半为1,然后利用勾股定理即可解决问题.
【详解】解:根据图形可知:长方形的长是正方形的对角线为2,长方形的宽是正方形对角线的一半为1,
∴根据勾股定理可知,长方形的对角线长:.
故答案为:.
【点睛】本题主要考查了正方形的性质,七巧板,矩形的性质,勾股定理,解决本题的关键是所拼成的正方形的特点确定长方形的长与宽.
14.
【分析】先确定正方形的中心O与各边的所有点的连线中的最大值与最小值,然后结合旋转的条件即可求解.
【详解】解:如图1,设的中点为E,连接OA,OE,则AE=OE=1,∠AEO=90°,.
∴点O与正方形边上的所有点的连线中,
最小,等于1,最大,等于.
∵,
∴点P与正方形边上的所有点的连线中,
如图2所示,当点E落在上时,最大值PE=PO-EO=2-1=1;
如图3所示,当点A落在上时,最小值.
∴当正方形ABCD绕中心O旋转时,点P到正方形的距离d的取值范围是.
故答案为:
【点睛】本题考查了新定义、正方形的性质、勾股定理等知识点,准确理解新定义的含义和熟知正方形的性质是解题的关键.
15.
【分析】设大正方形的边长为2a,则大等腰直角三角形的腰长为,中等腰直角三角形的腰长为a,小等腰直角三角形的腰长为,小正方形的边长为,平行四边形的长边为a,短边为,用含有a的代数式表示点A的横坐标,表示点F的坐标,确定a值即可.
【详解】设大正方形的边长为2a,则大等腰直角三角形的腰长为,中等腰直角三角形的腰长为a,小等腰直角三角形的腰长为,小正方形的边长为,平行四边形的长边为a,短边为,如图,过点F作FG⊥x轴,垂足为G, 点F作FH⊥y轴,垂足为H, 过点A作AQ⊥x轴,垂足为Q,延长大等腰直角三角形的斜边交x轴于点N,交FH于点M,
根据题意,得OC==,CD=a,DQ=,
∵点A的横坐标为1,
∴+a+=1,
∴a=;
根据题意,得FM=PM=,MH=,
∴FH==;
∴MT=2a-,BT=2a-,
∴TN=-a,
∴MN=MT+TN=2a-+-a==,
∵点F在第二象限,
∴点F的坐标为(-,)
故答案为:(-,).
【点睛】本题考查了七巧板的意义,合理设出未知数,用未知数表示各个图形的边长,点AA的横坐标,点F的坐标是解题的关键.
16.或
【分析】分两种情况讨论,当交于点H和交于点H时,利用等腰直角三角形的性质以及三角形的面积公式即可求解.
【详解】解:∵在等腰直角三角形中,
∴,
当交于点H时,
∴,
∴设,
由题意得,
解得,即,
∴点C移动的距离为,
所用时间为;
当交于点H时,
∴,
同理,得,
∴,
∵在等腰直角三角形中,,,
∴,
∴点C移动的距离为,
所用时间为;
故答案为:或.
【点睛】本题主要考查了平移的性质,勾股定理以及等腰直角三角形的性质,解题的关键是掌握等腰直角三角形的性质.
17.
【分析】①连接,根据正方形的性质证出,再利用勾股定理求出正方形边长,再通过计算即可求出最后结果.②连接,过点作于点,根据题意证出,,得出当点与重合时,点与重合,当点与重合时,最大,通过计算即可求出.
【详解】如解图,连接,
∵四边形与四边形为正方形,∴,,,∴,即,∴,
∴,设,正方形的边长为1,
∴,,正方形边长为,
∵为中点,
∴,
∴,
∴,
∴,∵,
∴,解得,
∴;
②连接,过点作于点,
∴,∴,
∵,∴,∴点,,在同一直线上,
∴,∴,
∴,∴,,
∴,即,
∴,∴,
∴点的运动轨迹是一条线段,当点与重合时,点与重合,当点与重合时,最大,,
∴点的运动路径的长是.
【点睛】本题主要考查了正方形性质,全等三角形的证明和性质,勾股定理等知识,采用数形结合的方法,熟悉以上定理是解题的关键.
18. ##135度
【分析】(1)连接,证明是等边三角形,求得,利用等腰三角形的性质求得,据此即可求解;
(2)在上取点G,使,连接,利用边角边证明,推出,得到当D、E、G三点共线时,有最小值,最小值为的长,在中,利用勾股定理即可求解.
【详解】解:(1)连接,
∵四边形是正方形,
∴,,
∵,由旋转的性质知,,
∴是等边三角形,
∴,,
∴,
∴,
∴;
故答案为:;
(2)∵,
∴,
在上取点G,使,连接.
在和中,,
∴,
∴,
∴,当D、E、G三点共线时,有最小值,最小值为的长,在中,,,
∴,即的最小值为.
故答案为:.
【点睛】本题考查了旋转的性质,等边三角形的判定和性质,勾股定理,全等三角形的判定和性质,第2问作出合适的辅助线构造全等三角形是解题的关键.
19.(1)见解析
(2)
【分析】(1)根据正方形和菱形的性质可得,根据即可得证;
(2)连接交于点,勾股定理求得,,根据菱形的性质可得,进而求得正方形和菱形的对角线的长度,根据即可求解.
【详解】(1)证明:正方形和菱形,
,
在与中
()
(2)如图,连接交于点,
,即AB=4,
,
在中,
,
,
在中,,
,
在中,,
,
,
.
【点睛】本题考查了菱形的性质,正方形的性质,勾股定理,,掌握以上知识是解题的关键.
20.(1)
(2)
(3),或,或
【分析】(1)如图,连接,,由对称知,
由四边形是正方形得,所以,从而;
(2)如图,连接,,,,交于点H,由轴对称知,,,,可证得,由勾股定理得,中,,中,,从而;
(3)由勾股定理,,分情况讨论:当点F在D,H之间时,;当点D在F,H之间时,;当点H在F,D之间时,.
【详解】(1)解:如图,连接,,
∵点关于直线的对称点为点,
∴,关于对称,
∴,,
∵四边形是正方形,
∴,
∴ ,
∴.
故答案为:20.
(2)解:;理由如下:
如图,由轴对称知,,,
而
∴
∴
∴
∴中,
中,
∴即;
(3)∵,,
∴,
∵,
∴,
如图,当点F在D,H之间时,,
如图,当点D在F,H之间时,
如图,当点H在F,D之间时,
【点睛】本题考查轴对称的性质,正方形的性质,等腰三角形知识,勾股定理等,将运动状态的所有可能考虑完备,分类讨论是解题的关键.
21.(1)
(2)
(3)
【分析】(1)首先由折叠的性质可得,再由等腰三角形的性质可求解;
(2)首先由折叠的性质可得,,再由等腰三角形的性质可得,,最后根据角度关系即可求解;
(3)首先由等腰直角三角形的性质和直角三角形的性质可求的长,由勾股定理可求的长,最后根据面积和差关系可求解.
【详解】(1),,,
,
将沿折叠得到,
,
,
∴△ABE是等边三角形,
,
故答案为:60;
(2),理由如下:
将沿折叠得到,
,,
,,
,
,
,
;
(3)如图,连接,
,点是的中点,
,
,,
,,
,
,
,
,
.
【点睛】本题考查了等腰直角三角形的性质,直角三角形的性质,折叠的性质等知识,解题的关键是熟练掌握相关性质并能够灵活运用.
22.(1)不存在,理由见详解
(2)
(3)1
【分析】(1)根据“等形点”的概念,采用反证法即可判断;
(2)过A点作AM⊥BC于点M,根据“等形点”的性质可得AB=CD=,OA=OC=5,OB=7=OD,设MO=a,则BM=BO-MO=7-a,在Rt△ABM和Rt△AOM中,利用勾股定理即可求出AM,则在Rt△AMC中利用勾股定理即可求出AC;
(3)根据“等形点”的性质可得OF=OH,OE=OG,∠EOF=∠GOH,再根据,可得∠EOF=∠OEH,∠GOH=∠EHO,即有∠OEH=∠OHE,进而有OE=OH,可得OF=OG,则问题得解.
【详解】(1)不存在,
理由如下:
假设正方形ABCD存在“等形点”点O,即存在△OAB≌△OCD,
∵在正方形ABCD中,点O在边BC上,
∴∠ABO=90°,
∵△OAB≌△OCD,
∴∠ABO=∠CDO=90°,
∴CD⊥DO,
∵CD⊥BC,
∴,
∵O点在BC上,
∴DO与BC交于点O,
∴假设不成立,
故正方形不存在“等形点”;
(2)如图,过A点作AM⊥BC于点M,如图,
∵O点是四边形ABCD的“等形点”,
∴△OAB≌△OCD,
∴AB=CD,OA=OC,OB=OD,∠AOB=∠COD,
∵,OA=5,BC=12,
∴AB=CD=,OA=OC=5,
∴OB=BC-OC=12-5=7=OD,
∵AM⊥BC,
∴∠AMO=90°=∠AMB,
∴设MO=a,则BM=BO-MO=7-a,
∴在Rt△ABM和Rt△AOM中,,
∴,即,
解得:,即,
∴MC=MO+OC=,
∴在Rt△AMC中,,
即AC的长为;
(3)如图,
∵O点是四边形EFGH的“等形点”,
∴△OEF≌△OGH,
∴OF=OH,OE=OG,∠EOF=∠GOH,
∵,
∴∠EOF=∠OEH,∠GOH=∠EHO,
∴根据∠EOF=∠GOH有∠OEH=∠OHE,
∴OE=OH,
∵OF=OH,OE=OG,
∴OF=OG,
∴.
【点睛】本题考查了全等三角形的性质、勾股定理、正方形的性质、平行的性质等知识,充分利用全等三角形的性质是解答本题的关键.
23.(1)AC=BC+CD;理由见详解;
(2)CB+CD=AC;理由见详解;
(3)或
【分析】(1)如图1中,延长CD到点E,使DE=BC,连接AE.证明△ADE≌△ABC(SAS),推出∠DAE=∠BAC,AE=AC,推出△ACE的等边三角形,可得结论;
(2)结论:CB+CD=AC.如图2中,过点A作AM⊥CD于点M,AN⊥CB交CB的延长线于点N.证明△AMD≌△ANB(AAS),推出DM=BN,AM=AN,证明Rt△ACM≌Rt△ACN(HL),推出CM=CN,可得结论;
(3)分两种情形:如图3-1中,当∠CDA=75°时,过点O作OP⊥CB于点P,CQ⊥CD于点Q.如图3-2中,当∠CBD=75°时,分别求解即可.
【详解】(1)证明:如图1中,延长CD到点E,使DE=BC,连接AE.
∵∠BAD+∠BCD=180°,
∴∠B+∠ADC=180°,
∵∠ADE+∠ADC=180°
∴∠B=∠ADE,
在△ADE和△ABC中,
,
∴△ADE≌△ABC(SAS),
∴∠DAE=∠BAC,AE=AC,
∴∠CAE=∠BAD=60°,
∴△ACE的等边三角形,
∴CE=AC,
∵CE=DE+CD,
∴AC=BC+CD;
(2)解:结论:CB+CD=AC.
理由:如图2中,过点A作AM⊥CD于点M,AN⊥CB交CB的延长线于点N.
∵∠DAB=∠DCB=90°,
∴∠CDA+∠CBA=180°,
∵∠ABN+∠ABC=180°,
∴∠D=∠ABN,
∵∠AMD=∠N=90°,AD=AB,
∴△AMD≌△ANB(AAS),
∴DM=BN,AM=AN,
∵AM⊥CD,AN⊥CN,
∴∠ACD=∠ACB=45°,
∴AC=CM,
∵AC=AC.AM=AN,
∴Rt△ACM≌Rt△ACN(HL),
∴CM=CN,
∴CB+CD=CNBN+CM+DM=2CM=AC;
(3)解:如图3-1中,当∠CDA=75°时,过点O作OP⊥CB于点P,CQ⊥CD于点Q.
∵∠CDA=75°,∠ADB=45°,
∴∠CDB=30°,
∵∠DCB=90°,
∴CD=CB,
∵∠DCO=∠BCO=45°,OP⊥CB,OQ⊥CD,
∴OP=OQ,
∴,
∴,
∵AB=AD=,∠DAB=90°,
∴BD=AD=2,
∴OD=.
如图3-2中,当∠CBD=75°时,
同法可证,,
综上所述,满足条件的OD的长为或.
【点睛】本题属于四边形综合题,考查了全等三角形的判定和性质,解直角三角形,等边三角形的判定和性质,角平分线的性质定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.
24.(1)见解析;(2)是等腰直角三角形,理由见解析;(3)的形状不改变,见解析
【分析】(1)连接,,,根据正方形的性质求出,证明,推出,再利用余角的性质求出,推出即可;
(2)根据正方形的性质直接得到,推出,得到是等腰直角三角形;
(3)延长至点M,使,连接,证明,得到,推出,设交于点H,交于点N,得到,由得到,推出,进而得到,再证明,得到,,证得,再由,根据等腰三角形的三线合一的性质求出,即可证得是等腰直角三角形.
【详解】(1)证明:连接,,,如图,
∵四边形,都是正方形,
∴,
∴,
∵四边形是正方形,
∴,
又∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴,即点P恰为的中点;
(2)是等腰直角三角形,理由如下:
∵四边形,都是正方形,
∴
∴,
∴是等腰直角三角形;
(3)的形状不改变,
延长至点M,使,连接,
∵四边形、四边形都是正方形,
∴,,
∵点P为的中点,
∴,
∵,
∴,
∴,
∴,,
∴,
设交于点H,交于点N,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
又∵,
∴,
∴,,
∵,
∴,即,
∵,
∴,即,
∴,
∴,
∴,
∴是等腰直角三角形.
【点睛】此题考查了正方形的性质,全等三角形的判定和性质,等腰直角三角形的判定和性质,平行线的性质等,(3)中作辅助线利用中点构造全等三角形是解题的难点,熟练掌握各性质和判定定理是解题的关键.
答案第26页,共27页
答案第27页,共27页
【要点回顾】
一、正方形的性质
(1)四边都相等;(2)四个角都是直角;(3)对称线垂直平分且相等;(4)是轴对称图形,也是中心对称图形.
二、正方形的判定
(1)定义法:有一组邻边相等并且有一个内角是直角的平行四边形;
(2)判定定理1:对角线相等的菱形是正方形;
(3)判定定理2:对角线相互垂直的矩形是正方形;
(4)判定定理3:有一个内角是直角的菱形是正方形;
(5)判定定理4:有一组邻边相等的矩形是正方形.
一、单选题
(2023·四川自贡·统考中考真题)
1.如图,边长为的正方形两边与坐标轴正半轴重合,点的坐标是( )
A. B. C. D.
(2022·浙江嘉兴·统考中考真题)
2.“方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得到正方形,形成一个“方胜”图案,则点D,之间的距离为( )
A.1cm B.2cm C.(-1)cm D.(2-1)cm
(2023·四川广安·统考中考真题)
3.下列说法正确的是( )
A.三角形的一个外角等于两个内角的和
B.对角线相等且互相垂直的四边形是正方形
C.在一组数据11,9,7,8,6,8,12,8中,众数和中位数都是8
D.甲乙两组各10名同学参加“安全知识竞赛”,若两组同学的平均成绩相同,甲组的方差,乙组的方差,则甲组同学的成绩比乙组同学的成绩稳定
(2022·浙江绍兴·统考中考真题)
4.如图,在平行四边形中,,,,是对角线上的动点,且,,分别是边,边上的动点.下列四种说法:①存在无数个平行四边形;②存在无数个矩形;③存在无数个菱形;④存在无数个正方形.其中正确的个数是( )
A.1 B.2 C.3 D.4
(2022·山东滨州·统考中考真题)
5.正方形的对角线相交于点O(如图1),如果绕点O按顺时针方向旋转,其两边分别与边相交于点E、F(如图2),连接EF,那么在点E由B到A的过程中,线段EF的中点G经过的路线是( )
A.线段 B.圆弧 C.折线 D.波浪线
(2021·甘肃兰州·统考中考真题)
6.如图,将图1中的菱形纸片沿对角线剪成4个直角三角形,拼成如图2的四边形(相邻纸片之间不重叠,无缝隙).若四边形的面积为13,中间空白处的四边形的面积为1,直角三角形的两条直角边分别为和,则( )
A.12 B.13 C.24 D.25
(2021·江苏泰州·统考中考真题)
7.如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设,则 为( )
A.2α B.90°﹣α C.45°+α D.90°﹣α
(2021·广西玉林·统考中考真题)
8.一个四边形顺次添加下列中的三个条件便得到正方形:
a.两组对边分别相等 b.一组对边平行且相等
c.一组邻边相等 d.一个角是直角
顺次添加的条件:①a→c→d②b→d→c③a→b→c
则正确的是:( )
A.仅① B.仅③ C.①② D.②③
(2021·湖南常德·统考中考真题)
9.如图,已知F、E分别是正方形的边与的中点,与交于P.则下列结论成立的是( )
A. B. C. D.
(2021·重庆·统考中考真题)
10.如图,把含30°的直角三角板PMN放置在正方形ABCD中,,直角顶点P在正方形ABCD的对角线BD上,点M,N分别在AB和CD边上,MN与BD交于点O,且点O为MN的中点,则的度数为( )
A.60° B.65° C.75° D.80°
二、填空题
(2023·湖南·统考中考真题)
11.七巧板是我国民间广为流传的一种益智玩具,某同学用边长为的正方形纸板制作了一副七巧板(如图),由5个等腰直角三角形,1个正方形和1个平行四边形组成.则图中阴影部分的面积为 .
(2022·江苏常州·统考中考真题)
12.如图,将一个边长为的正方形活动框架(边框粗细忽略不计)扭动成四边形,对角线是两根橡皮筋,其拉伸长度达到时才会断裂.若,则橡皮筋 断裂(填“会”或“不会”,参考数据:).
(2022·江西·统考中考真题)
13.沐沐用七巧板拼了一个对角线长为2的正方形,再用这副七巧板拼成一个长方形(如图所示),则长方形的对角线长为 .
(2021·上海·统考中考真题)
14.定义:在平面内,一个点到图形的距离是这个点到这个图上所有点的最短距离,在平面内有一个正方形,边长为2,中心为O,在正方形外有一点,当正方形绕着点O旋转时,则点P到正方形的最短距离d的取值范围为 .
(2021·浙江金华·统考中考真题)
15.如图,在平面直角坐标系中,有一只用七巧板拼成的“猫”,三角形①的边BC及四边形②的边CD都在x轴上,“猫”耳尖E在y轴上.若“猫”尾巴尖A的横坐标是1,则“猫”爪尖F的坐标是 .
(2023·河南南阳·统考三模)
16.如图,在正方形中,,在等腰直角三角形中,,.边与在同一直线上..若正方形以的速度沿直线向右运动,经过 ,此三角形和正方形重叠部分的面积是.
(2023·贵州贵阳·校考一模)
17.如图,在正方形中,,点为上一动点,连接,以为边在上方作正方形.若点是的中点,且,则的长是 ;点从点到点的运动过程中,点所运动的路径长是 .
(2023·安徽宣城·校考三模)
18.在正方形中,将绕点B逆时针旋转得到,连接.
(1)当时, ;
(2)在上取点F,使,连接.若,当时,的最小值为 .
三、解答题
(2022·贵州遵义·统考中考真题)
19.将正方形和菱形按照如图所示摆放,顶点与顶点重合,菱形的对角线经过点,点,分别在,上.
(1)求证:;
(2)若,求的长.
(2023·湖北十堰·统考中考真题)
20.过正方形的顶点作直线,点关于直线的对称点为点,连接,直线交直线于点.
(1)如图1,若,则___________;
(2)如图1,请探究线段,,之间的数量关系,并证明你的结论;
(3)在绕点转动的过程中,设,请直接用含的式子表示的长.
(2022·新疆·统考中考真题)
21.如图,在巾,,点O为BC的中点,点D是线段OC上的动点(点D不与点O,C重合),将沿AD折叠得到,连接BE.
(1)当时,___________;
(2)探究与之间的数量关系,并给出证明;
(3)设,的面积为x,以AD为边长的正方形的面积为y,求y关于x的函数解析式.
(2022·江苏常州·统考中考真题)
22.在四边形中,是边上的一点.若,则点叫做该四边形的“等形点”.
(1)正方形_______“等形点”(填“存在”或“不存在”);
(2)如图,在四边形中,边上的点是四边形的“等形点”.已知,,,连接,求的长;
(3)在四边形中,EH//FG.若边上的点是四边形的“等形点”,求的值.
(2022·辽宁朝阳·统考中考真题)
23.【思维探究】如图1,在四边形ABCD中,∠BAD=60°,∠BCD=120°,AB=AD,连接AC.求证:BC+CD=AC.
(1)小明的思路是:延长CD到点E,使DE=BC,连接AE.根据∠BAD+∠BCD=180°,推得∠B+∠ADC=180°,从而得到∠B=∠ADE,然后证明ADE≌ABC,从而可证BC+CD=AC,请你帮助小明写出完整的证明过程.
(2)【思维延伸】如图2,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,连接AC,猜想BC,CD,AC之间的数量关系,并说明理由.
(3)【思维拓展】在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD=,AC与BD相交于点O.若四边形ABCD中有一个内角是75°,请直接写出线段OD的长.
(2023·湖南·统考中考真题)
24.问题情境:小红同学在学习了正方形的知识后,进一步进行以下探究活动:在正方形的边上任意取一点G,以为边长向外作正方形,将正方形绕点B顺时针旋转.
特例感知:
(1)当在上时,连接相交于点P,小红发现点P恰为的中点,如图①.针对小红发现的结论,请给出证明;
(2)小红继续连接,并延长与相交,发现交点恰好也是中点P,如图②,根据小红发现的结论,请判断的形状,并说明理由;
规律探究:
(3)如图③,将正方形绕点B顺时针旋转,连接,点P是中点,连接,,,的形状是否发生改变?请说明理由.
试卷第8页,共9页
试卷第1页,共9页
参考答案:
1.C
【分析】根据正方形的性质,结合坐标的意义即可求解.
【详解】解:∵边长为的正方形两边与坐标轴正半轴重合,
∴
∴,
故选:C.
【点睛】本题考查了坐标与图形,熟练掌握正方形的性质,数形结合是解题的关键.
2.D
【分析】先求出BD,再根据平移性质求得=1cm,然后由求解即可.
【详解】解:由题意,BD=cm,
由平移性质得=1cm,
∴点D,之间的距离为==()cm,
故选:D.
【点睛】本题考查平移性质、正方形的性质,熟练掌握平移性质是解答的关键.
3.C
【分析】根据三角形的外角定理,正方形的判定,众数和中位数的定义,方差的意义判断即可.
【详解】解:A.三角形的一个外角等于与它不相邻两个内角的和,故选项A错误;
B.要加上 “对角线互相平分”这个条件,故选项B错误;
C.这列数据从小到大排列为6,7,8,8,8,9,11,12,
8出现了3次,故众数是8,中位数是,
故选项C正确;
D.方差越小,数据越稳定,故选项D错误.
故选:C.
【点睛】本题考查了三角形的外角定理,正方形的判定,众数和中位数的定义,方差的意义等知识,本题的关键是熟练掌握这些知识点,并能灵活运用.
4.C
【分析】根据题意作出合适的辅助线,然后逐一分析即可.
【详解】
如图,连接AC、与BD交于点O,连接ME,MF,NF,EN,MN,
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
∵BE=DF
∴OE=OF
∵点E、F时BD上的点,
∴只要M,N过点O,
那么四边形MENF就是平行四边形
∴存在无数个平行四边形MENF,故①正确;
只要MN=EF,MN过点O,则四边形MENF是矩形,
∵点E、F是BD上的动点,
∴存在无数个矩形MENF,故②正确;
只要MN⊥EF,MN过点O,则四边形MENF是菱形;
∵点E、F是BD上的动点,
∴存在无数个菱形MENF,故③正确;
只要MN=EF,MN⊥EF,MN过点O,
则四边形MENF是正方形,
而符合要求的正方形只有一个,故④错误;
故选:C
【点睛】本题考查正方形的判定、菱形的判定、矩形的判定、平行四边形的判定、解答本题的关键时明确题意,作出合适的辅助线.
5.A
【分析】连接,根据题意可知则线段EF的中点G经过的路线是的线段垂直平分线的一段,即线段
【详解】连接,根据题意可知,
,
∴点G在线段OB的垂直平分线上.
则线段EF的中点G经过的路线是的线段垂直平分线的一段,即线段.
故选:A.
【点睛】本题考查了线段垂直平分线的判定,直角三角形斜边上的中线等于斜边的一半,正方形的性质,掌握以上知识是解题的关键.
6.D
【分析】根据菱形的性质可得对角线互相垂直平分,进而可得4个直角三角形全等,结合已知条件和勾股定理求得,进而根据面积差以及三角形面积公式求得,最后根据完全平方公式即可求得.
【详解】菱形的对角线互相垂直平分,
个直角三角形全等;
,,
,
四边形是正方形,又正方形的面积为13,
正方形的边长为,
根据勾股定理,则,
中间空白处的四边形的面积为1,
个直角三角形的面积为,
,
,
,
.
故选D.
【点睛】本题考查了正方形的性质与判定,菱形的性质,勾股定理,完全平方公式,求得是解题的关键.
7.B
【分析】根据题意可得 ,从而 即可.
【详解】∵四边形APCD和四边形PBEF是正方形,
∴AP=CP,PF=PB,,
∴,
∴∠AFP=∠CBP,
又∵ ,
∴,
故选:B.
【点睛】本题主要考查了正方形的性质,全等三角形的判定,熟练掌握正方形的性质,全等三角形的判定方法是解题的关键.
8.C
【分析】根据题意及正方形的判定定理可直接进行排除选项.
【详解】解:①由两组对边分别相等可得该四边形是平行四边形,添加一组邻边相等可得该四边形是菱形,再添加一个角是直角则可得该四边形是正方形;正确,故符合题意;
②由一组对边平行且相等可得该四边形是平行四边形,添加一个角是直角可得该四边形是矩形,再添加一组邻边相等则可得该四边形是正方形;正确,故符合题意;
③a、b都为平行四边形的判定定理,故不能判定该四边形是正方形,故错误,不符合题意;
∴正确的有①②;
故选C.
【点睛】本题主要考查正方形的判定,熟练掌握正方形的判定定理是解题的关键.
9.C
【分析】根据正方形的性质,全等三角形的判定和性质以及等腰三角形的性质逐一判断即可.
【详解】解:∵四边形ABCD是正方形,
∴AB=BC=CD=CA,∠ABC=∠BCD=∠CDA=∠DAB=90°,
∵已知F、E分别是正方形ABCD的边AB与BC的中点,
∴BE=BC=AB
,
∴△ABE≌△DAF(SAS),
∴∠BAE=∠ADF,
∵∠ADF+∠AFD=90°,
∴∠BAE+∠AFD =90°,
∴∠APF=90°,
∴∠EAF+∠AFD=90°,故C选项正确,符合题意;
连接FC,
同理可证得△CBF≌△DAF(SAS),
∴∠BCF=∠ADF,
∴∠BCD-∠BCF=∠ADC-∠ADF,即90°-∠BCF=90°-∠ADF,
∴∠PDC=∠FCD>∠PCD,
∴PC>PD,故B选项错误,不符合题意;
∵AD>PD,
∴CD>PD,
∴∠DPC>∠DCP,
∴90°-∠DPC<90°-∠DCP,
∴∠CPE<∠PCE,
∴PE> CE,故D选项错误,不符合题意;
故选:C.
【点睛】本题考查了正方形的性质,全等三角形的判定与性质,等腰三角形的性质等知识.此题综合性很强,解题的关键是注意数形结合思想的应用.
10.C
【分析】根据斜边中线等于斜边一半,求出∠MPO=30°,再求出∠MOB和∠OMB的度数,即可求出的度数.
【详解】解:∵四边形ABCD是正方形中,
∴∠MBO=∠NDO=45°,
∵点O为MN的中点
∴OM=ON,
∵∠MPN=90°,
∴OM=OP,
∴∠PMN=∠MPO=30°,
∴∠MOB=∠MPO+∠PMN =60°,
∴∠BMO=180°-60°-45°=75°,
,
故选:C.
【点睛】本题考查了正方形的性质和直角三角形的性质、等腰三角形的性质,解题关键是熟练运用相关性质,根据角的关系进行计算.
11.
【分析】根据正方形的性质,以及七巧板的特点,求得的长,即可求解.
【详解】解:如图所示,
依题意,,
∴图中阴影部分的面积为
故答案为:.
【点睛】本题考查了正方形的性质,勾股定理,七巧板,熟练掌握以上知识是解题的关键.
12.不会
【分析】设扭动后对角线的交点为,根据正方形的性质,得出扭动后的四边形为菱形,利用菱形的性质及条件,得出为等边三角形,利用勾股定理算出,从而得到,再比较即可判断.
【详解】解:设扭动后对角线的交点为,如下图:
,
根据正方形的性质得,
得出扭动后的四边形四边相等为菱形,
cm,
为等边三角形,
cm,
cm,
cm,
根据菱形的对角线的性质:(cm),
,
不会断裂,
故答案为:不会.
【点睛】本题考查了正方形的性质、菱形的判定及性质、等边三角形、勾股定理,解题的关键是要掌握菱形的判定及性质.
13.
【分析】根据图形可得长方形的长是正方形的对角线为2,长方形的宽是正方形对角线的一半为1,然后利用勾股定理即可解决问题.
【详解】解:根据图形可知:长方形的长是正方形的对角线为2,长方形的宽是正方形对角线的一半为1,
∴根据勾股定理可知,长方形的对角线长:.
故答案为:.
【点睛】本题主要考查了正方形的性质,七巧板,矩形的性质,勾股定理,解决本题的关键是所拼成的正方形的特点确定长方形的长与宽.
14.
【分析】先确定正方形的中心O与各边的所有点的连线中的最大值与最小值,然后结合旋转的条件即可求解.
【详解】解:如图1,设的中点为E,连接OA,OE,则AE=OE=1,∠AEO=90°,.
∴点O与正方形边上的所有点的连线中,
最小,等于1,最大,等于.
∵,
∴点P与正方形边上的所有点的连线中,
如图2所示,当点E落在上时,最大值PE=PO-EO=2-1=1;
如图3所示,当点A落在上时,最小值.
∴当正方形ABCD绕中心O旋转时,点P到正方形的距离d的取值范围是.
故答案为:
【点睛】本题考查了新定义、正方形的性质、勾股定理等知识点,准确理解新定义的含义和熟知正方形的性质是解题的关键.
15.
【分析】设大正方形的边长为2a,则大等腰直角三角形的腰长为,中等腰直角三角形的腰长为a,小等腰直角三角形的腰长为,小正方形的边长为,平行四边形的长边为a,短边为,用含有a的代数式表示点A的横坐标,表示点F的坐标,确定a值即可.
【详解】设大正方形的边长为2a,则大等腰直角三角形的腰长为,中等腰直角三角形的腰长为a,小等腰直角三角形的腰长为,小正方形的边长为,平行四边形的长边为a,短边为,如图,过点F作FG⊥x轴,垂足为G, 点F作FH⊥y轴,垂足为H, 过点A作AQ⊥x轴,垂足为Q,延长大等腰直角三角形的斜边交x轴于点N,交FH于点M,
根据题意,得OC==,CD=a,DQ=,
∵点A的横坐标为1,
∴+a+=1,
∴a=;
根据题意,得FM=PM=,MH=,
∴FH==;
∴MT=2a-,BT=2a-,
∴TN=-a,
∴MN=MT+TN=2a-+-a==,
∵点F在第二象限,
∴点F的坐标为(-,)
故答案为:(-,).
【点睛】本题考查了七巧板的意义,合理设出未知数,用未知数表示各个图形的边长,点AA的横坐标,点F的坐标是解题的关键.
16.或
【分析】分两种情况讨论,当交于点H和交于点H时,利用等腰直角三角形的性质以及三角形的面积公式即可求解.
【详解】解:∵在等腰直角三角形中,
∴,
当交于点H时,
∴,
∴设,
由题意得,
解得,即,
∴点C移动的距离为,
所用时间为;
当交于点H时,
∴,
同理,得,
∴,
∵在等腰直角三角形中,,,
∴,
∴点C移动的距离为,
所用时间为;
故答案为:或.
【点睛】本题主要考查了平移的性质,勾股定理以及等腰直角三角形的性质,解题的关键是掌握等腰直角三角形的性质.
17.
【分析】①连接,根据正方形的性质证出,再利用勾股定理求出正方形边长,再通过计算即可求出最后结果.②连接,过点作于点,根据题意证出,,得出当点与重合时,点与重合,当点与重合时,最大,通过计算即可求出.
【详解】如解图,连接,
∵四边形与四边形为正方形,∴,,,∴,即,∴,
∴,设,正方形的边长为1,
∴,,正方形边长为,
∵为中点,
∴,
∴,
∴,
∴,∵,
∴,解得,
∴;
②连接,过点作于点,
∴,∴,
∵,∴,∴点,,在同一直线上,
∴,∴,
∴,∴,,
∴,即,
∴,∴,
∴点的运动轨迹是一条线段,当点与重合时,点与重合,当点与重合时,最大,,
∴点的运动路径的长是.
【点睛】本题主要考查了正方形性质,全等三角形的证明和性质,勾股定理等知识,采用数形结合的方法,熟悉以上定理是解题的关键.
18. ##135度
【分析】(1)连接,证明是等边三角形,求得,利用等腰三角形的性质求得,据此即可求解;
(2)在上取点G,使,连接,利用边角边证明,推出,得到当D、E、G三点共线时,有最小值,最小值为的长,在中,利用勾股定理即可求解.
【详解】解:(1)连接,
∵四边形是正方形,
∴,,
∵,由旋转的性质知,,
∴是等边三角形,
∴,,
∴,
∴,
∴;
故答案为:;
(2)∵,
∴,
在上取点G,使,连接.
在和中,,
∴,
∴,
∴,当D、E、G三点共线时,有最小值,最小值为的长,在中,,,
∴,即的最小值为.
故答案为:.
【点睛】本题考查了旋转的性质,等边三角形的判定和性质,勾股定理,全等三角形的判定和性质,第2问作出合适的辅助线构造全等三角形是解题的关键.
19.(1)见解析
(2)
【分析】(1)根据正方形和菱形的性质可得,根据即可得证;
(2)连接交于点,勾股定理求得,,根据菱形的性质可得,进而求得正方形和菱形的对角线的长度,根据即可求解.
【详解】(1)证明:正方形和菱形,
,
在与中
()
(2)如图,连接交于点,
,即AB=4,
,
在中,
,
,
在中,,
,
在中,,
,
,
.
【点睛】本题考查了菱形的性质,正方形的性质,勾股定理,,掌握以上知识是解题的关键.
20.(1)
(2)
(3),或,或
【分析】(1)如图,连接,,由对称知,
由四边形是正方形得,所以,从而;
(2)如图,连接,,,,交于点H,由轴对称知,,,,可证得,由勾股定理得,中,,中,,从而;
(3)由勾股定理,,分情况讨论:当点F在D,H之间时,;当点D在F,H之间时,;当点H在F,D之间时,.
【详解】(1)解:如图,连接,,
∵点关于直线的对称点为点,
∴,关于对称,
∴,,
∵四边形是正方形,
∴,
∴ ,
∴.
故答案为:20.
(2)解:;理由如下:
如图,由轴对称知,,,
而
∴
∴
∴
∴中,
中,
∴即;
(3)∵,,
∴,
∵,
∴,
如图,当点F在D,H之间时,,
如图,当点D在F,H之间时,
如图,当点H在F,D之间时,
【点睛】本题考查轴对称的性质,正方形的性质,等腰三角形知识,勾股定理等,将运动状态的所有可能考虑完备,分类讨论是解题的关键.
21.(1)
(2)
(3)
【分析】(1)首先由折叠的性质可得,再由等腰三角形的性质可求解;
(2)首先由折叠的性质可得,,再由等腰三角形的性质可得,,最后根据角度关系即可求解;
(3)首先由等腰直角三角形的性质和直角三角形的性质可求的长,由勾股定理可求的长,最后根据面积和差关系可求解.
【详解】(1),,,
,
将沿折叠得到,
,
,
∴△ABE是等边三角形,
,
故答案为:60;
(2),理由如下:
将沿折叠得到,
,,
,,
,
,
,
;
(3)如图,连接,
,点是的中点,
,
,,
,,
,
,
,
,
.
【点睛】本题考查了等腰直角三角形的性质,直角三角形的性质,折叠的性质等知识,解题的关键是熟练掌握相关性质并能够灵活运用.
22.(1)不存在,理由见详解
(2)
(3)1
【分析】(1)根据“等形点”的概念,采用反证法即可判断;
(2)过A点作AM⊥BC于点M,根据“等形点”的性质可得AB=CD=,OA=OC=5,OB=7=OD,设MO=a,则BM=BO-MO=7-a,在Rt△ABM和Rt△AOM中,利用勾股定理即可求出AM,则在Rt△AMC中利用勾股定理即可求出AC;
(3)根据“等形点”的性质可得OF=OH,OE=OG,∠EOF=∠GOH,再根据,可得∠EOF=∠OEH,∠GOH=∠EHO,即有∠OEH=∠OHE,进而有OE=OH,可得OF=OG,则问题得解.
【详解】(1)不存在,
理由如下:
假设正方形ABCD存在“等形点”点O,即存在△OAB≌△OCD,
∵在正方形ABCD中,点O在边BC上,
∴∠ABO=90°,
∵△OAB≌△OCD,
∴∠ABO=∠CDO=90°,
∴CD⊥DO,
∵CD⊥BC,
∴,
∵O点在BC上,
∴DO与BC交于点O,
∴假设不成立,
故正方形不存在“等形点”;
(2)如图,过A点作AM⊥BC于点M,如图,
∵O点是四边形ABCD的“等形点”,
∴△OAB≌△OCD,
∴AB=CD,OA=OC,OB=OD,∠AOB=∠COD,
∵,OA=5,BC=12,
∴AB=CD=,OA=OC=5,
∴OB=BC-OC=12-5=7=OD,
∵AM⊥BC,
∴∠AMO=90°=∠AMB,
∴设MO=a,则BM=BO-MO=7-a,
∴在Rt△ABM和Rt△AOM中,,
∴,即,
解得:,即,
∴MC=MO+OC=,
∴在Rt△AMC中,,
即AC的长为;
(3)如图,
∵O点是四边形EFGH的“等形点”,
∴△OEF≌△OGH,
∴OF=OH,OE=OG,∠EOF=∠GOH,
∵,
∴∠EOF=∠OEH,∠GOH=∠EHO,
∴根据∠EOF=∠GOH有∠OEH=∠OHE,
∴OE=OH,
∵OF=OH,OE=OG,
∴OF=OG,
∴.
【点睛】本题考查了全等三角形的性质、勾股定理、正方形的性质、平行的性质等知识,充分利用全等三角形的性质是解答本题的关键.
23.(1)AC=BC+CD;理由见详解;
(2)CB+CD=AC;理由见详解;
(3)或
【分析】(1)如图1中,延长CD到点E,使DE=BC,连接AE.证明△ADE≌△ABC(SAS),推出∠DAE=∠BAC,AE=AC,推出△ACE的等边三角形,可得结论;
(2)结论:CB+CD=AC.如图2中,过点A作AM⊥CD于点M,AN⊥CB交CB的延长线于点N.证明△AMD≌△ANB(AAS),推出DM=BN,AM=AN,证明Rt△ACM≌Rt△ACN(HL),推出CM=CN,可得结论;
(3)分两种情形:如图3-1中,当∠CDA=75°时,过点O作OP⊥CB于点P,CQ⊥CD于点Q.如图3-2中,当∠CBD=75°时,分别求解即可.
【详解】(1)证明:如图1中,延长CD到点E,使DE=BC,连接AE.
∵∠BAD+∠BCD=180°,
∴∠B+∠ADC=180°,
∵∠ADE+∠ADC=180°
∴∠B=∠ADE,
在△ADE和△ABC中,
,
∴△ADE≌△ABC(SAS),
∴∠DAE=∠BAC,AE=AC,
∴∠CAE=∠BAD=60°,
∴△ACE的等边三角形,
∴CE=AC,
∵CE=DE+CD,
∴AC=BC+CD;
(2)解:结论:CB+CD=AC.
理由:如图2中,过点A作AM⊥CD于点M,AN⊥CB交CB的延长线于点N.
∵∠DAB=∠DCB=90°,
∴∠CDA+∠CBA=180°,
∵∠ABN+∠ABC=180°,
∴∠D=∠ABN,
∵∠AMD=∠N=90°,AD=AB,
∴△AMD≌△ANB(AAS),
∴DM=BN,AM=AN,
∵AM⊥CD,AN⊥CN,
∴∠ACD=∠ACB=45°,
∴AC=CM,
∵AC=AC.AM=AN,
∴Rt△ACM≌Rt△ACN(HL),
∴CM=CN,
∴CB+CD=CNBN+CM+DM=2CM=AC;
(3)解:如图3-1中,当∠CDA=75°时,过点O作OP⊥CB于点P,CQ⊥CD于点Q.
∵∠CDA=75°,∠ADB=45°,
∴∠CDB=30°,
∵∠DCB=90°,
∴CD=CB,
∵∠DCO=∠BCO=45°,OP⊥CB,OQ⊥CD,
∴OP=OQ,
∴,
∴,
∵AB=AD=,∠DAB=90°,
∴BD=AD=2,
∴OD=.
如图3-2中,当∠CBD=75°时,
同法可证,,
综上所述,满足条件的OD的长为或.
【点睛】本题属于四边形综合题,考查了全等三角形的判定和性质,解直角三角形,等边三角形的判定和性质,角平分线的性质定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.
24.(1)见解析;(2)是等腰直角三角形,理由见解析;(3)的形状不改变,见解析
【分析】(1)连接,,,根据正方形的性质求出,证明,推出,再利用余角的性质求出,推出即可;
(2)根据正方形的性质直接得到,推出,得到是等腰直角三角形;
(3)延长至点M,使,连接,证明,得到,推出,设交于点H,交于点N,得到,由得到,推出,进而得到,再证明,得到,,证得,再由,根据等腰三角形的三线合一的性质求出,即可证得是等腰直角三角形.
【详解】(1)证明:连接,,,如图,
∵四边形,都是正方形,
∴,
∴,
∵四边形是正方形,
∴,
又∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴,即点P恰为的中点;
(2)是等腰直角三角形,理由如下:
∵四边形,都是正方形,
∴
∴,
∴是等腰直角三角形;
(3)的形状不改变,
延长至点M,使,连接,
∵四边形、四边形都是正方形,
∴,,
∵点P为的中点,
∴,
∵,
∴,
∴,
∴,,
∴,
设交于点H,交于点N,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
又∵,
∴,
∴,,
∵,
∴,即,
∵,
∴,即,
∴,
∴,
∴,
∴是等腰直角三角形.
【点睛】此题考查了正方形的性质,全等三角形的判定和性质,等腰直角三角形的判定和性质,平行线的性质等,(3)中作辅助线利用中点构造全等三角形是解题的难点,熟练掌握各性质和判定定理是解题的关键.
答案第26页,共27页
答案第27页,共27页
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
