八年级数学上册试题 2.2 轴对称的性质 苏科版(含答案)
文档属性
| 名称 | 八年级数学上册试题 2.2 轴对称的性质 苏科版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 513.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 00:00:00 | ||
图片预览


文档简介
2.2 轴对称的性质
一、单选题
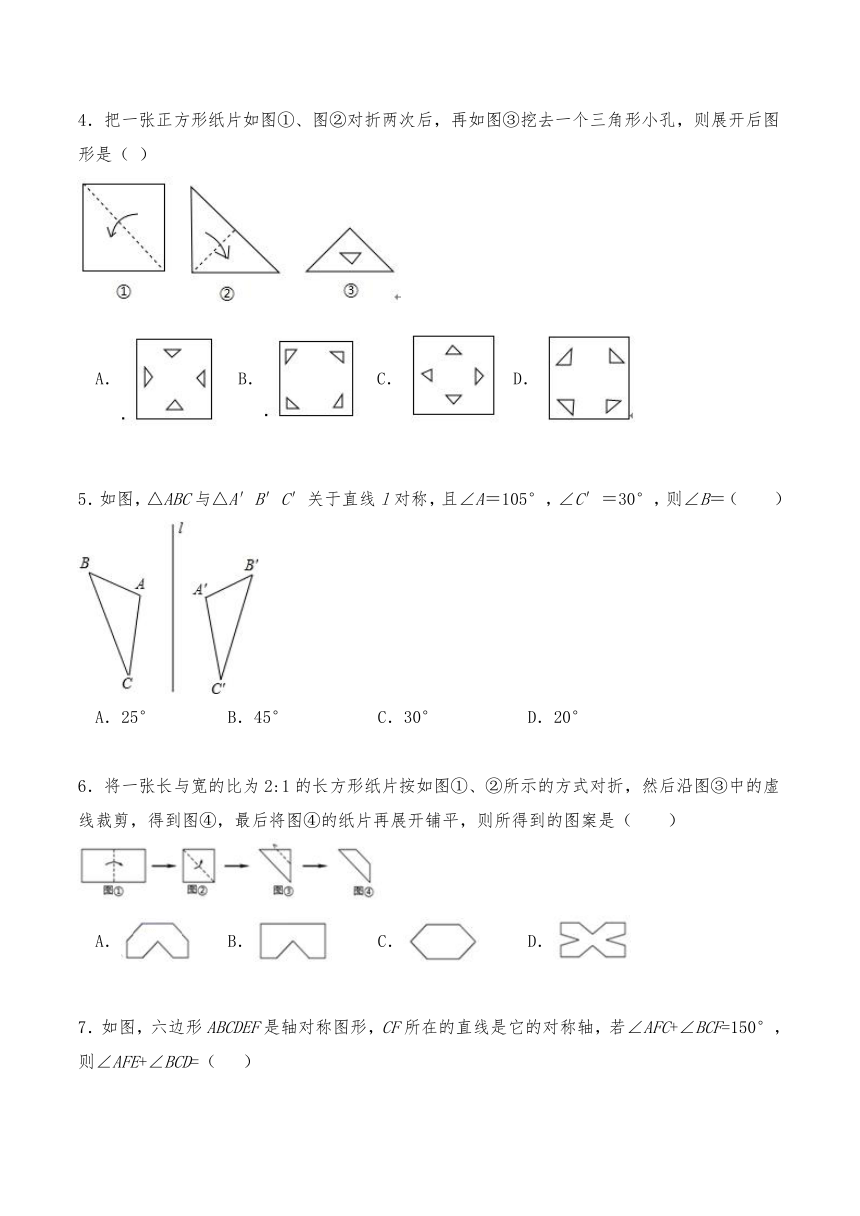
1.如图,若△ABC 与△A′B′C′关于直线 MN 对称,BB′交 MN 于点 O,则下列说法不一定正确的是( )
A.AC=A′C′ B.BO=B′O C.AA′⊥MN D.AB∥B′C′
2.如图,直线是四边形的对称轴,点是直线上的点,下列判断错误的是( )
A. B. C. D.
3.如图,△ABC与△A′B′C′关于直线l对称,且∠A=78°,∠C′=48°,则∠B的度数为( )
A.48° B.54° C.74° D.78°
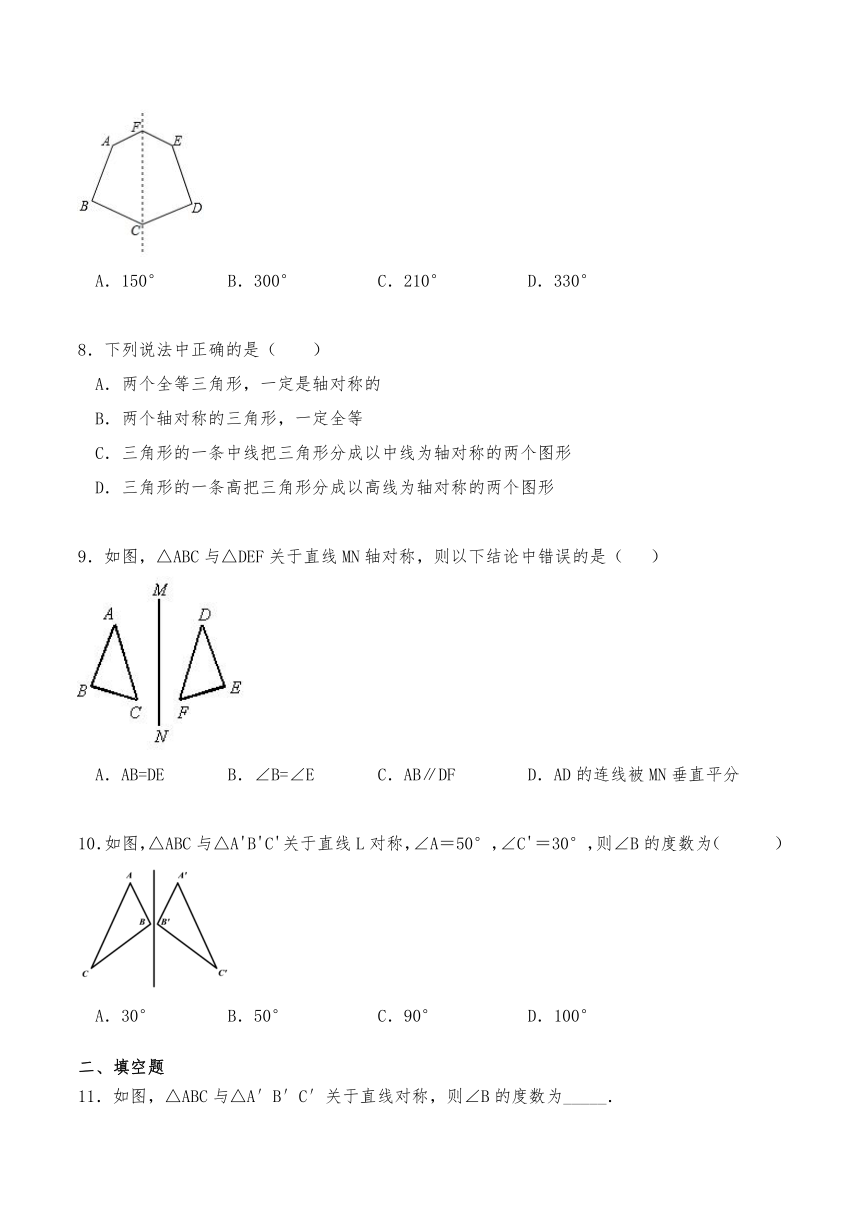
4.把一张正方形纸片如图①、图②对折两次后,再如图③挖去一个三角形小孔,则展开后图形是( )
A.B.C.D.
5.如图,△ABC与△A′B′C′关于直线l对称,且∠A=105°,∠C′=30°,则∠B=( )
A.25° B.45° C.30° D.20°
6.将一张长与宽的比为2:1的长方形纸片按如图①、②所示的方式对折,然后沿图③中的虚线裁剪,得到图④,最后将图④的纸片再展开铺平,则所得到的图案是( )
A. B. C. D.
7.如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠BCF=150°,则∠AFE+∠BCD=( )
A.150° B.300° C.210° D.330°
8.下列说法中正确的是( )
A.两个全等三角形,一定是轴对称的
B.两个轴对称的三角形,一定全等
C.三角形的一条中线把三角形分成以中线为轴对称的两个图形
D.三角形的一条高把三角形分成以高线为轴对称的两个图形
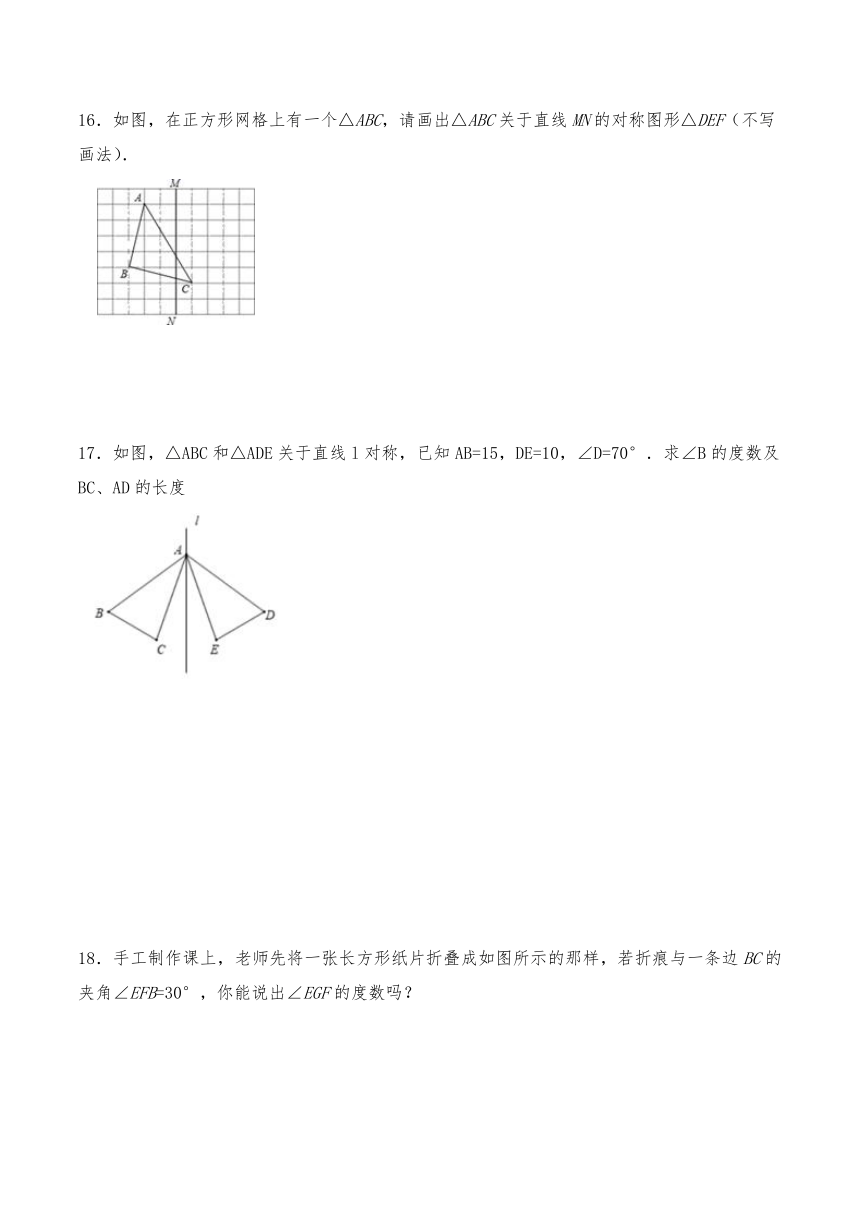
9.如图,△ABC与△DEF关于直线MN轴对称,则以下结论中错误的是( )
A.AB=DE B.∠B=∠E C.AB∥DF D.AD的连线被MN垂直平分
10.如图,△ABC与△A'B'C'关于直线L对称,∠A=50°,∠C'=30°,则∠B的度数为( )
A.30° B.50° C.90° D.100°
二、填空题
11.如图,△ABC与△A′B′C′关于直线对称,则∠B的度数为_____.
12.如图,四边形ABCD沿直线l对折后互相重合,如果AD∥BC,有下列结论:①AB∥CD ②AB=CD ③AB⊥BC ④AO=OC其中正确的结论是_______________. (把你认为正确的结论的序号都填上)
13.已知与关于直线对称,且度,,那么=______度.
14.一辆汽车的牌号在水中的倒影如图所示,则这辆汽车的牌号应为 .
三、解答题
15.如图,在所给的方格图中,完成下列各题(用直尺画图,保留作图痕迹)
(1)画出格点△ABC关于直线DE对称的△A1B1C1;
(2)求△ABC的面积;
(3)在DE上面出点P,使PA+PC最小.
16.如图,在正方形网格上有一个△ABC,请画出△ABC关于直线MN的对称图形△DEF(不写画法).
17.如图,△ABC和△ADE关于直线l对称,已知AB=15,DE=10,∠D=70°.求∠B的度数及BC、AD的长度
18.手工制作课上,老师先将一张长方形纸片折叠成如图所示的那样,若折痕与一条边BC的夹角∠EFB=30°,你能说出∠EGF的度数吗?
19.在公路上建筑一车站,使它到、两村庄的距离和最短.(保留画图痕迹)
20.如图1和图2,在三角形纸片中,点,分别在边,上,沿折叠,点落在点的位置.
(1)如图1,当点落在边上时,与之间的数量关系为______(只填序号),并说明理由;
① ② ③
(2)如图2,当点落在内部时,直接写出与,之间的数量关系.
21.如图1,三角形中,,,.点D是边上的定点,点E在边上运动,沿折叠三角形,点C落在点G处.
(1)如图2,若,求的度数.
(2)如图3,若,求的度数.
(3)当三角形的三边与三角形的三边有一组边平行时,直接写出其他所有情况下的度数.
答案
一、单选题
D.D.B.C.B.A.B.B.C.D.
二、填空题
11.105°
12.①②④
13.60.
14.W17906.
三、解答题
15.
(1)如图所示:△A1B1C1,即为所求;
(2)△ABC的面积为:2×3﹣×2×2﹣×1×1﹣×1×3=2;
(3)如图所示:点P即为所求.
16.
解:如图所示,△DEF即为所求.
17.
解:∵△ABC和△ADE关于直线l对称,
∴AB=AD,BC=DE,∠B=∠D
又∵AB=15,DE=10,∠D=70°
∴∠B=70°,BC=10,AD=15,
答:∠B=70°,BC=10、AD=15.
18.解:因为AD∥BC(已知),
所以∠DEF=∠EFG=30°(两直线平行,内错角相等),
因为∠GEF=∠DEF=30°(对折后重合部分相等),
所以∠DEG=2∠DEF=60°,
所以∠EGC=180°-∠DEG=180°-60°=120°(两直线平行,同旁内角互补).
19.①连接交于点,点就是所求的点;
②画出点关于直线的对称点,连接交于点,连接,
、关于直线对称,
,
,
由两点之间线段最短可知,线段的长即为的最小值,故点即为所求点.
20.解:(1)根据折叠的性质可得,
∵,
∴;
故答案为③;
(2),理由如下:
延长交AC于点F,如图所示:
由折叠的性质可得,
∴根据三角形外角的性质可得,
∴,
∵,
∴.
21.解:(1)由折叠可知:
∠C=∠DGE=26°,∠CDE=∠GDE,
∵DE∥AB,AB⊥BC,
∴DE⊥BC,则G在BC上,
∴∠CDE=∠A=∠GDE=64°,
∴∠ADG=180°-64°×2=52°;
(2)由折叠可知:∠C=∠DGE=26°,∠CDE=∠GDE,∠DEC=∠DEG,
∵GE∥AB,
∴∠B=∠CEG=∠BEG=90°,
∴∠EFG=90°-26°=64°,
∵∠A=64°,∠B=90°,
∴∠ADG=360°-64°-90°-64°=142°;
(3)如图,DG∥AB,
则∠ADG=180°-∠A=116°;
如图,DG∥BC,
∠ADG=∠C=26°;
如图,EG∥AC,
∠ADG=∠G=∠C=26°;
如图,EG∥AB,
∴∠A=∠CFE=64°,∠B=∠CEG=90°,
由折叠可知:∠DEG=∠DEC=45°,
∴∠CDE=180°-45°-26°=109°=∠EDG,
∴∠EDF=180°-109°=71°,
∴∠ADG=109°-71°=38°;
如图,DG∥AB,
∴∠ADG=∠A=64°;
综上:其他所有情况下∠ADG的度数为116°或26°或38°或64°.
一、单选题
1.如图,若△ABC 与△A′B′C′关于直线 MN 对称,BB′交 MN 于点 O,则下列说法不一定正确的是( )
A.AC=A′C′ B.BO=B′O C.AA′⊥MN D.AB∥B′C′
2.如图,直线是四边形的对称轴,点是直线上的点,下列判断错误的是( )
A. B. C. D.
3.如图,△ABC与△A′B′C′关于直线l对称,且∠A=78°,∠C′=48°,则∠B的度数为( )
A.48° B.54° C.74° D.78°
4.把一张正方形纸片如图①、图②对折两次后,再如图③挖去一个三角形小孔,则展开后图形是( )
A.B.C.D.
5.如图,△ABC与△A′B′C′关于直线l对称,且∠A=105°,∠C′=30°,则∠B=( )
A.25° B.45° C.30° D.20°
6.将一张长与宽的比为2:1的长方形纸片按如图①、②所示的方式对折,然后沿图③中的虚线裁剪,得到图④,最后将图④的纸片再展开铺平,则所得到的图案是( )
A. B. C. D.
7.如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠BCF=150°,则∠AFE+∠BCD=( )
A.150° B.300° C.210° D.330°
8.下列说法中正确的是( )
A.两个全等三角形,一定是轴对称的
B.两个轴对称的三角形,一定全等
C.三角形的一条中线把三角形分成以中线为轴对称的两个图形
D.三角形的一条高把三角形分成以高线为轴对称的两个图形
9.如图,△ABC与△DEF关于直线MN轴对称,则以下结论中错误的是( )
A.AB=DE B.∠B=∠E C.AB∥DF D.AD的连线被MN垂直平分
10.如图,△ABC与△A'B'C'关于直线L对称,∠A=50°,∠C'=30°,则∠B的度数为( )
A.30° B.50° C.90° D.100°
二、填空题
11.如图,△ABC与△A′B′C′关于直线对称,则∠B的度数为_____.
12.如图,四边形ABCD沿直线l对折后互相重合,如果AD∥BC,有下列结论:①AB∥CD ②AB=CD ③AB⊥BC ④AO=OC其中正确的结论是_______________. (把你认为正确的结论的序号都填上)
13.已知与关于直线对称,且度,,那么=______度.
14.一辆汽车的牌号在水中的倒影如图所示,则这辆汽车的牌号应为 .
三、解答题
15.如图,在所给的方格图中,完成下列各题(用直尺画图,保留作图痕迹)
(1)画出格点△ABC关于直线DE对称的△A1B1C1;
(2)求△ABC的面积;
(3)在DE上面出点P,使PA+PC最小.
16.如图,在正方形网格上有一个△ABC,请画出△ABC关于直线MN的对称图形△DEF(不写画法).
17.如图,△ABC和△ADE关于直线l对称,已知AB=15,DE=10,∠D=70°.求∠B的度数及BC、AD的长度
18.手工制作课上,老师先将一张长方形纸片折叠成如图所示的那样,若折痕与一条边BC的夹角∠EFB=30°,你能说出∠EGF的度数吗?
19.在公路上建筑一车站,使它到、两村庄的距离和最短.(保留画图痕迹)
20.如图1和图2,在三角形纸片中,点,分别在边,上,沿折叠,点落在点的位置.
(1)如图1,当点落在边上时,与之间的数量关系为______(只填序号),并说明理由;
① ② ③
(2)如图2,当点落在内部时,直接写出与,之间的数量关系.
21.如图1,三角形中,,,.点D是边上的定点,点E在边上运动,沿折叠三角形,点C落在点G处.
(1)如图2,若,求的度数.
(2)如图3,若,求的度数.
(3)当三角形的三边与三角形的三边有一组边平行时,直接写出其他所有情况下的度数.
答案
一、单选题
D.D.B.C.B.A.B.B.C.D.
二、填空题
11.105°
12.①②④
13.60.
14.W17906.
三、解答题
15.
(1)如图所示:△A1B1C1,即为所求;
(2)△ABC的面积为:2×3﹣×2×2﹣×1×1﹣×1×3=2;
(3)如图所示:点P即为所求.
16.
解:如图所示,△DEF即为所求.
17.
解:∵△ABC和△ADE关于直线l对称,
∴AB=AD,BC=DE,∠B=∠D
又∵AB=15,DE=10,∠D=70°
∴∠B=70°,BC=10,AD=15,
答:∠B=70°,BC=10、AD=15.
18.解:因为AD∥BC(已知),
所以∠DEF=∠EFG=30°(两直线平行,内错角相等),
因为∠GEF=∠DEF=30°(对折后重合部分相等),
所以∠DEG=2∠DEF=60°,
所以∠EGC=180°-∠DEG=180°-60°=120°(两直线平行,同旁内角互补).
19.①连接交于点,点就是所求的点;
②画出点关于直线的对称点,连接交于点,连接,
、关于直线对称,
,
,
由两点之间线段最短可知,线段的长即为的最小值,故点即为所求点.
20.解:(1)根据折叠的性质可得,
∵,
∴;
故答案为③;
(2),理由如下:
延长交AC于点F,如图所示:
由折叠的性质可得,
∴根据三角形外角的性质可得,
∴,
∵,
∴.
21.解:(1)由折叠可知:
∠C=∠DGE=26°,∠CDE=∠GDE,
∵DE∥AB,AB⊥BC,
∴DE⊥BC,则G在BC上,
∴∠CDE=∠A=∠GDE=64°,
∴∠ADG=180°-64°×2=52°;
(2)由折叠可知:∠C=∠DGE=26°,∠CDE=∠GDE,∠DEC=∠DEG,
∵GE∥AB,
∴∠B=∠CEG=∠BEG=90°,
∴∠EFG=90°-26°=64°,
∵∠A=64°,∠B=90°,
∴∠ADG=360°-64°-90°-64°=142°;
(3)如图,DG∥AB,
则∠ADG=180°-∠A=116°;
如图,DG∥BC,
∠ADG=∠C=26°;
如图,EG∥AC,
∠ADG=∠G=∠C=26°;
如图,EG∥AB,
∴∠A=∠CFE=64°,∠B=∠CEG=90°,
由折叠可知:∠DEG=∠DEC=45°,
∴∠CDE=180°-45°-26°=109°=∠EDG,
∴∠EDF=180°-109°=71°,
∴∠ADG=109°-71°=38°;
如图,DG∥AB,
∴∠ADG=∠A=64°;
综上:其他所有情况下∠ADG的度数为116°或26°或38°或64°.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
