24.2.2 圆的切线的性质和判定 专题训练五(含答案)
文档属性
| 名称 | 24.2.2 圆的切线的性质和判定 专题训练五(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-13 00:00:00 | ||
图片预览



文档简介
圆的切线的性质和判定专题训练五
一、选择题(本大题共10小题,每小题3分,共30分)
1. 若把路面看成直线,则行驶在水平路面上的汽车转动的车轮与地面的位置关系是( ).
A. 相交 B. 相切 C. 相离 D. 不确定
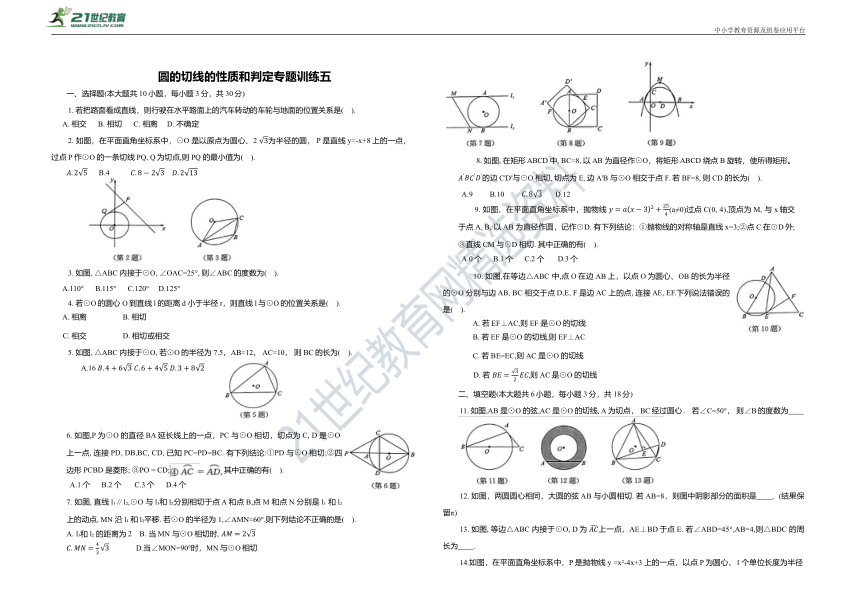
2. 如图,在平面直角坐标系中,⊙O 是以原点为圆心、2 为半径的圆, P是直线y=-x+8上的一点, 过点 P 作⊙O 的一条切线PQ, Q为切点,则 PQ 的最小值为( ).
B.4
3. 如图, △ABC 内接于⊙O, ∠OAC=25°, 则∠ABC的度数为( ).
A.110° B.115° C.120° D.125°
4. 若⊙O的圆心O到直线l的距离d 小于半径r,则直线l与⊙O的位置关系是( ).
A. 相离 B. 相切
C. 相交 D. 相切或相交
5. 如图, △ABC 内接于⊙O, 若⊙O的半径为 7.5,AB=12, AC=10, 则BC的长为( ).
A.16
6. 如图,P为⊙O 的直径BA 延长线上的一点,PC 与⊙O 相切,切点为C, D 是⊙O 上一点, 连接 PD, DB,BC, CD, 已知 PC=PD=BC. 有下列结论:①PD 与⊙O 相切;②四边形PCBD 是菱形; ③PO = CD; 其中正确的有( ).
A.1个 B.2个 C.3个 D.4个
7. 如图, 直线l ∥l ,⊙O 与l 和l 分别相切于点 A 和点B,点M 和点N 分别是l 和l 上的动点, MN 沿l 和l 平移. 若⊙O 的半径为 1,∠AMN=60°,则下列结论不正确的是( ).
A. l 和l 的距离为2 B. 当 MN 与⊙O 相切时,
D.当∠MON=90°时,MN与⊙O相切
8. 如图, 在矩形 ABCD中, BC=8, 以 AB 为直径作⊙O,将矩形 ABCD 绕点B 旋转,使所得矩形。 的边C'D'与⊙O 相切, 切点为E, 边 A'B 与⊙O 相交于点 F. 若BF=8, 则CD 的长为( ).
A.9 B.10 D.12
9. 如图,在平面直角坐标系中,抛物线 (a≠0)过点C(0, 4),顶点为 M, 与x轴交于点A, B, 以AB 为直径作圆,记作⊙D. 有下列结论:①抛物线的对称轴是直线x=3;②点C在⊙D外;③直线 CM 与⊙D 相切. 其中正确的有( ).
A.0个 B.1个 C.2个 D.3个
10. 如图,在等边△ABC 中,点O在边AB上,以点O为圆心、OB 的长为半径的⊙O 分别与边 AB, BC 相交于点D,E, F 是边 AC 上的点, 连接 AE, EF.下列说法错误的是( ).
A. 若 EF⊥AC,则 EF 是⊙O 的切线
B. 若EF 是⊙O 的切线,则 EF⊥AC
C. 若BE=EC,则AC 是⊙O 的切线
D. 若 则AC是⊙O 的切线
二、填空题(本大题共6小题,每小题3分,共18分)
11. 如图,AB 是⊙O 的弦,AC 是⊙O 的切线, A 为切点, BC经过圆心. 若∠C=50°, 则∠B的度数为
12. 如图,两圆圆心相同,大圆的弦AB 与小圆相切. 若AB=8,则图中阴影部分的面积是 . (结果保留π)
13. 如图, 等边△ABC 内接于⊙O, D为 上一点,AE⊥BD于点E. 若∠ABD=45°,AB=4,则△BDC 的周长为 .
14.如图,在平面直角坐标系中,P 是抛物线y =x -4x+3上的一点,以点P为圆心、1个单位长度为半径作⊙P,当⊙P与x轴相切时,点P的坐标为 .
15.如图,以△ABC的边AB为直径的⊙O 恰好过 BC的中点D,过点D作DE⊥AC于点E,连接OD, AD. 有下列结论: ①OD∥AC;②∠B=∠C;③2OA=AC;④DE是⊙O的切线;⑤∠EDA=∠B. 其中正确的是 . (填序号) 16. 如图, 在矩形 ABCD 中,AB=4 cm, AD=12cm,动点 P 以 1 cm/s 的速度从点 C 沿折线C-D-A匀速运动,到点A 运动停止. 以点 P 为圆心作半径为 的⊙P, 当⊙P 与对角线BD相切时,点 P的运动时间为 s.
三、解答题(本大题共6小题,共52分. 解答时应写出必要的文字说明、证明过程或演算步骤)
17.(6分)如图,在 Rt△ABC 中, ∠ACB=90°,O-为边BC上一点,以点O为圆心、OB 的长为半径的⊙O 与边AB相交于点D,连接 DC,且DC为⊙O 的切线.
(1)求证: DC=AC;
(2)若DC=DB,⊙O 的半径为 1,求DC 的长.
18.(6分)如图,AB 是⊙O 的直径,射线 BC 交⊙O 于点D,E 是AD上一点,且AE=DE,过点E作EF⊥BC 于点F,延长FE 交 BA 的延长线于点G,连接OE.
(1)求证: GF 是⊙O 的切线;
(2)若 求△GOE 的面积.
21.(10分)如图,AB 是⊙O 的直径,AM 和 BN 是⊙O的两条切线,D是AM上一点,连接OD,过点B作BE∥OD交⊙O 于点E,连接 DE 并延长交BN 于点C.
(1)求证: DE 是⊙O 的切线;
(2)若AD=1, BC=4,求直径 AB 的长.
22.(12分)如图,在△ABC 中,以边 BC 为直径的⊙O交边AB于点D,E为BD的中点, CE 与边 AB 相交于点F,且AF=AC.
(1)求证: AC 是⊙O 的切线;
中小学教育资源及组卷应用平台
(2)若 BC=8, BF=4,求 DF 的长.
专题训练五 圆的切线的性质和判定
1. B 2. A 3. B 4. C 5. C 6. C 7. B 8. B 9. C 10. C
11.20° 12.16π
14.(2+ , 1)或 或(2, -1)
15.①②③④⑤ 或
17.(1)如图, 连接OD.
∵CD 是⊙O 的切线,
∴CD⊥OD,
∴∠ODC=90°,
∴∠BDO+∠ADC=90°.
∵∠ACB=90°,
∴∠A+∠B=90°.
∵OB=OD,
∴∠B=∠ODB,
∴∠A=∠ADC,
∴CD=AC.
(2)∵DC=DB,
∴∠DCB=∠DBC,
∴∠DCB=∠BDO.
∵∠DCB+∠DBC+∠BDO+∠ODC=180°,
∴∠DCB=∠DBC=∠BDO=30°,
∵OC=2OD=2,
18. (1)如图,连接 BE.
∴∠1=∠2.
∵∠2=∠3,
∴∠1=∠3,
∴OE∥BF.
∵BF⊥GF,
∴OE⊥GF,
∴GF 是⊙O 的切线.
(2)设 OA=OE=r,
在 Rt△GOE 中,
解得r=3,
19.如图,延长 DO交CA 的延长线于点F,过点O作OE⊥CD于点E, 连接AO, BO.
∵AC, BD 是⊙O 的切线,
∴OA⊥AC, OB⊥BD.
∵AC∥BD,
∴A, O, B三点共线, ∠F=∠BDO.在△AFO与△BDO中,
∴△AFO≌△BDO(AAS),
∴OD=OF.
∵∠COD=90°,
∴∠COF=90°,
∴CF=CD,
∴∠OCA=∠OCE.
又∵OA⊥AC,OE⊥CD,
∴OE=OA,
∴CD 是⊙O 的切线.
20.(1)如图①,过点 D作DE⊥AB 于点E.
∵∠ACB=90°, BD是∠ABC的平分线,
∴CD=DE,
∴⊙D与AB 相切.
(2)四边形 CDEF 是菱形.
理由: 如图②,连接DE, EF, FC.
∵∠ACB=90°,CD 是⊙D 的半径,
∴BC 是⊙D 的切线.
∵AB 是⊙D 的切线,
∴BC=BE,
在△CBF 与△EBF中,
∴△CBF≌△EBF(SAS),
∴CF=EF, ∠CFB=∠EFB,
∴∠CFD=∠EFD.
∵CF ∥DE,
∴∠CFD=∠EDF,
∴∠EDF=∠EFD,
∴DE=EF,
∴DE=CF,
∴四边形 CDEF 是菱形.
21.(1)连接OE,如图①.
∵OA=OE=OB,
∴∠OBE=∠OEB.
∵OD∥BE,
∴∠AOD=∠OBE, ∠OEB=∠DOE.
∴∠AOD=∠EOD.
在△AOD 和△EOD中,
∴△AOD≌△EOD(SAS),
∴∠OAD=∠OED.
∵AM是⊙O 的切线,
∴∠OAD=90°,
∴∠OED=90°, 即OE⊥DE.
∵OE为⊙O 的半径,
∴DE 是⊙O 的切线.
(2)过点 D 作 DH⊥BC 于点 H, 如图②.
∵AM 和BN 是⊙O 的两条切线,
∴∠DAB=∠ABH=∠DHB=90°,
∴四边形 ABHD 是矩形,
∴AB=DH, AD=BH.
∵AD=1, BC=4,
∴BH=1, CH=4-1=3.
∵AM和BN是⊙O 的两条切线,DE切⊙O 于点E,
∴DE=AD=1, CE=BC=4,
∴DC=1+4=5.
在Rt△DHC中,由勾股定理得 =4, 即AB=4.
22.(1)连接BE, 如图①.
∵BC为⊙O 的直径,
∴∠BEC=90°,
∴∠EBF+∠EFB=90°.
∵E为lBD的中点,
∴∠EBF=∠BCE.
∵AC=AF,
∴∠ACF=∠AFC.
∵∠AFC=∠EFB,
∴∠EFB=∠ACF,
∴∠ACF+∠BCE=∠EFB+∠EBF=90°,
∴OC⊥AC.
∵BC为⊙O 的直径、
∴AC 是⊙O 的切线.
(2)连接CD,如图②.
设AC=AF=x,
在 Rt△ACB 中, ∵AC +BC =AB ,
∴x +8 =(x+4) ,解得x=6,
∴AC=6, AB=10.
∵BC 是⊙O 的直径,
∴∠CDB=90°, 即 CD⊥AB.
在Rt△CDB 中,∵CD +BD =BC ,
一、选择题(本大题共10小题,每小题3分,共30分)
1. 若把路面看成直线,则行驶在水平路面上的汽车转动的车轮与地面的位置关系是( ).
A. 相交 B. 相切 C. 相离 D. 不确定
2. 如图,在平面直角坐标系中,⊙O 是以原点为圆心、2 为半径的圆, P是直线y=-x+8上的一点, 过点 P 作⊙O 的一条切线PQ, Q为切点,则 PQ 的最小值为( ).
B.4
3. 如图, △ABC 内接于⊙O, ∠OAC=25°, 则∠ABC的度数为( ).
A.110° B.115° C.120° D.125°
4. 若⊙O的圆心O到直线l的距离d 小于半径r,则直线l与⊙O的位置关系是( ).
A. 相离 B. 相切
C. 相交 D. 相切或相交
5. 如图, △ABC 内接于⊙O, 若⊙O的半径为 7.5,AB=12, AC=10, 则BC的长为( ).
A.16
6. 如图,P为⊙O 的直径BA 延长线上的一点,PC 与⊙O 相切,切点为C, D 是⊙O 上一点, 连接 PD, DB,BC, CD, 已知 PC=PD=BC. 有下列结论:①PD 与⊙O 相切;②四边形PCBD 是菱形; ③PO = CD; 其中正确的有( ).
A.1个 B.2个 C.3个 D.4个
7. 如图, 直线l ∥l ,⊙O 与l 和l 分别相切于点 A 和点B,点M 和点N 分别是l 和l 上的动点, MN 沿l 和l 平移. 若⊙O 的半径为 1,∠AMN=60°,则下列结论不正确的是( ).
A. l 和l 的距离为2 B. 当 MN 与⊙O 相切时,
D.当∠MON=90°时,MN与⊙O相切
8. 如图, 在矩形 ABCD中, BC=8, 以 AB 为直径作⊙O,将矩形 ABCD 绕点B 旋转,使所得矩形。 的边C'D'与⊙O 相切, 切点为E, 边 A'B 与⊙O 相交于点 F. 若BF=8, 则CD 的长为( ).
A.9 B.10 D.12
9. 如图,在平面直角坐标系中,抛物线 (a≠0)过点C(0, 4),顶点为 M, 与x轴交于点A, B, 以AB 为直径作圆,记作⊙D. 有下列结论:①抛物线的对称轴是直线x=3;②点C在⊙D外;③直线 CM 与⊙D 相切. 其中正确的有( ).
A.0个 B.1个 C.2个 D.3个
10. 如图,在等边△ABC 中,点O在边AB上,以点O为圆心、OB 的长为半径的⊙O 分别与边 AB, BC 相交于点D,E, F 是边 AC 上的点, 连接 AE, EF.下列说法错误的是( ).
A. 若 EF⊥AC,则 EF 是⊙O 的切线
B. 若EF 是⊙O 的切线,则 EF⊥AC
C. 若BE=EC,则AC 是⊙O 的切线
D. 若 则AC是⊙O 的切线
二、填空题(本大题共6小题,每小题3分,共18分)
11. 如图,AB 是⊙O 的弦,AC 是⊙O 的切线, A 为切点, BC经过圆心. 若∠C=50°, 则∠B的度数为
12. 如图,两圆圆心相同,大圆的弦AB 与小圆相切. 若AB=8,则图中阴影部分的面积是 . (结果保留π)
13. 如图, 等边△ABC 内接于⊙O, D为 上一点,AE⊥BD于点E. 若∠ABD=45°,AB=4,则△BDC 的周长为 .
14.如图,在平面直角坐标系中,P 是抛物线y =x -4x+3上的一点,以点P为圆心、1个单位长度为半径作⊙P,当⊙P与x轴相切时,点P的坐标为 .
15.如图,以△ABC的边AB为直径的⊙O 恰好过 BC的中点D,过点D作DE⊥AC于点E,连接OD, AD. 有下列结论: ①OD∥AC;②∠B=∠C;③2OA=AC;④DE是⊙O的切线;⑤∠EDA=∠B. 其中正确的是 . (填序号) 16. 如图, 在矩形 ABCD 中,AB=4 cm, AD=12cm,动点 P 以 1 cm/s 的速度从点 C 沿折线C-D-A匀速运动,到点A 运动停止. 以点 P 为圆心作半径为 的⊙P, 当⊙P 与对角线BD相切时,点 P的运动时间为 s.
三、解答题(本大题共6小题,共52分. 解答时应写出必要的文字说明、证明过程或演算步骤)
17.(6分)如图,在 Rt△ABC 中, ∠ACB=90°,O-为边BC上一点,以点O为圆心、OB 的长为半径的⊙O 与边AB相交于点D,连接 DC,且DC为⊙O 的切线.
(1)求证: DC=AC;
(2)若DC=DB,⊙O 的半径为 1,求DC 的长.
18.(6分)如图,AB 是⊙O 的直径,射线 BC 交⊙O 于点D,E 是AD上一点,且AE=DE,过点E作EF⊥BC 于点F,延长FE 交 BA 的延长线于点G,连接OE.
(1)求证: GF 是⊙O 的切线;
(2)若 求△GOE 的面积.
21.(10分)如图,AB 是⊙O 的直径,AM 和 BN 是⊙O的两条切线,D是AM上一点,连接OD,过点B作BE∥OD交⊙O 于点E,连接 DE 并延长交BN 于点C.
(1)求证: DE 是⊙O 的切线;
(2)若AD=1, BC=4,求直径 AB 的长.
22.(12分)如图,在△ABC 中,以边 BC 为直径的⊙O交边AB于点D,E为BD的中点, CE 与边 AB 相交于点F,且AF=AC.
(1)求证: AC 是⊙O 的切线;
中小学教育资源及组卷应用平台
(2)若 BC=8, BF=4,求 DF 的长.
专题训练五 圆的切线的性质和判定
1. B 2. A 3. B 4. C 5. C 6. C 7. B 8. B 9. C 10. C
11.20° 12.16π
14.(2+ , 1)或 或(2, -1)
15.①②③④⑤ 或
17.(1)如图, 连接OD.
∵CD 是⊙O 的切线,
∴CD⊥OD,
∴∠ODC=90°,
∴∠BDO+∠ADC=90°.
∵∠ACB=90°,
∴∠A+∠B=90°.
∵OB=OD,
∴∠B=∠ODB,
∴∠A=∠ADC,
∴CD=AC.
(2)∵DC=DB,
∴∠DCB=∠DBC,
∴∠DCB=∠BDO.
∵∠DCB+∠DBC+∠BDO+∠ODC=180°,
∴∠DCB=∠DBC=∠BDO=30°,
∵OC=2OD=2,
18. (1)如图,连接 BE.
∴∠1=∠2.
∵∠2=∠3,
∴∠1=∠3,
∴OE∥BF.
∵BF⊥GF,
∴OE⊥GF,
∴GF 是⊙O 的切线.
(2)设 OA=OE=r,
在 Rt△GOE 中,
解得r=3,
19.如图,延长 DO交CA 的延长线于点F,过点O作OE⊥CD于点E, 连接AO, BO.
∵AC, BD 是⊙O 的切线,
∴OA⊥AC, OB⊥BD.
∵AC∥BD,
∴A, O, B三点共线, ∠F=∠BDO.在△AFO与△BDO中,
∴△AFO≌△BDO(AAS),
∴OD=OF.
∵∠COD=90°,
∴∠COF=90°,
∴CF=CD,
∴∠OCA=∠OCE.
又∵OA⊥AC,OE⊥CD,
∴OE=OA,
∴CD 是⊙O 的切线.
20.(1)如图①,过点 D作DE⊥AB 于点E.
∵∠ACB=90°, BD是∠ABC的平分线,
∴CD=DE,
∴⊙D与AB 相切.
(2)四边形 CDEF 是菱形.
理由: 如图②,连接DE, EF, FC.
∵∠ACB=90°,CD 是⊙D 的半径,
∴BC 是⊙D 的切线.
∵AB 是⊙D 的切线,
∴BC=BE,
在△CBF 与△EBF中,
∴△CBF≌△EBF(SAS),
∴CF=EF, ∠CFB=∠EFB,
∴∠CFD=∠EFD.
∵CF ∥DE,
∴∠CFD=∠EDF,
∴∠EDF=∠EFD,
∴DE=EF,
∴DE=CF,
∴四边形 CDEF 是菱形.
21.(1)连接OE,如图①.
∵OA=OE=OB,
∴∠OBE=∠OEB.
∵OD∥BE,
∴∠AOD=∠OBE, ∠OEB=∠DOE.
∴∠AOD=∠EOD.
在△AOD 和△EOD中,
∴△AOD≌△EOD(SAS),
∴∠OAD=∠OED.
∵AM是⊙O 的切线,
∴∠OAD=90°,
∴∠OED=90°, 即OE⊥DE.
∵OE为⊙O 的半径,
∴DE 是⊙O 的切线.
(2)过点 D 作 DH⊥BC 于点 H, 如图②.
∵AM 和BN 是⊙O 的两条切线,
∴∠DAB=∠ABH=∠DHB=90°,
∴四边形 ABHD 是矩形,
∴AB=DH, AD=BH.
∵AD=1, BC=4,
∴BH=1, CH=4-1=3.
∵AM和BN是⊙O 的两条切线,DE切⊙O 于点E,
∴DE=AD=1, CE=BC=4,
∴DC=1+4=5.
在Rt△DHC中,由勾股定理得 =4, 即AB=4.
22.(1)连接BE, 如图①.
∵BC为⊙O 的直径,
∴∠BEC=90°,
∴∠EBF+∠EFB=90°.
∵E为lBD的中点,
∴∠EBF=∠BCE.
∵AC=AF,
∴∠ACF=∠AFC.
∵∠AFC=∠EFB,
∴∠EFB=∠ACF,
∴∠ACF+∠BCE=∠EFB+∠EBF=90°,
∴OC⊥AC.
∵BC为⊙O 的直径、
∴AC 是⊙O 的切线.
(2)连接CD,如图②.
设AC=AF=x,
在 Rt△ACB 中, ∵AC +BC =AB ,
∴x +8 =(x+4) ,解得x=6,
∴AC=6, AB=10.
∵BC 是⊙O 的直径,
∴∠CDB=90°, 即 CD⊥AB.
在Rt△CDB 中,∵CD +BD =BC ,
同课章节目录
