二次函数 专题训练（含答案）

二次函数专题训练
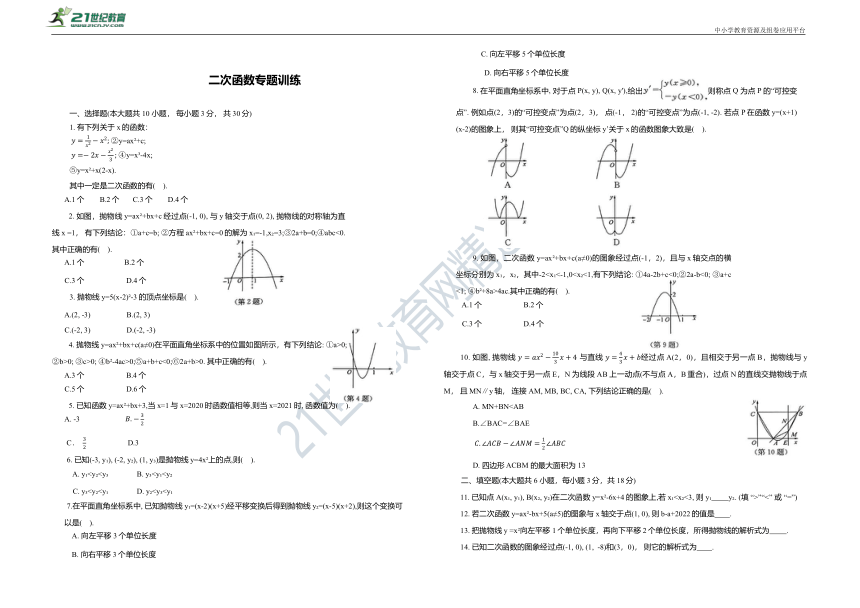
一、选择题(本大题共 10 小题， 每小题3分， 共30分)
1. 有下列关于x的函数：
②y=ax +c;
④y=x -4x;
⑤y=x +x(2-x).
其中一定是二次函数的有( ).
A.1个 B.2个 C.3个 D.4个
2. 如图，抛物线y=ax +bx+c经过点(-1, 0), 与 y轴交于点(0, 2), 抛物线的对称轴为直线 x =1， 有下列结论：①a+c=b; ②方程ax +bx+c=0的解为x =-1,x =3;③2a+b=0;④abc<0.其中正确的有( ).
A.1个 B.2个
C.3个 D.4个
3. 抛物线y=5(x-2) -3的顶点坐标是( ).
A.(2, -3) B.(2, 3)
C.(-2, 3) D.(-2, -3)
4. 抛物线y=ax +bx+c(a≠0)在平面直角坐标系中的位置如图所示，有下列结论: ①a>0; ②b>0; ③c>0; ④b -4ac>0;⑤a+b+c<0;⑥2a+b>0. 其中正确的有( ).
A.3个 B.4个
C.5个 D.6个
5. 已知函数y=ax +bx+3,当x=1与x=2020时函数值相等,则当x=2021时, 函数值为( ).
A. -3
C． D.3
6. 已知(-3, y ), (-2, y ), (1, y )是抛物线y=4x 上的点,则( ).
A. y C. y 7.在平面直角坐标系中, 已知抛物线y =(x-2)(x+5)经平移变换后得到抛物线y =(x-5)(x+2),则这个变换可以是( ).
A. 向左平移3个单位长度
B. 向右平移3个单位长度
C. 向左平移5个单位长度
D. 向右平移5个单位长度
8. 在平面直角坐标系中, 对于点 P(x, y), Q(x, y'),给出则称点 Q 为点 P 的“可控变点”. 例如点(2，3)的“可控变点”为点(2，3)， 点(-1， 2)的“可控变点”为点(-1, -2). 若点 P在函数y=(x+1)(x-2)的图象上， 则其“可控变点”Q的纵坐标y’关于x的函数图象大致是( ).
9. 如图，二次函数y=ax +bx+c(a≠0)的图象经过点(-1，2)，且与x轴交点的横坐标分别为x ，x ，其中-24ac.其中正确的有( ).
A.1个 B.2个
C.3个 D.4个
10. 如图, 抛物线 与直线 经过点A(2，0)，且相交于另一点B，抛物线与y轴交于点C，与x轴交于另一点E，N为线段AB上一动点(不与点A，B重合)，过点 N的直线交抛物线于点M， 且MN∥y轴， 连接AM, MB, BC, CA, 下列结论正确的是( ).
A. MN+BNB.∠BAC=∠BAE
D. 四边形 ACBM 的最大面积为 13
二、填空题(本大题共6 小题，每小题3分，共18分)
11. 已知点A(x , y ), B(x , y )在二次函数 y=x -6x+4的图象上,若x ”“<” 或 “=”)
12. 若二次函数y=ax -bx+5(a≠5)的图象与 x轴交于点(1, 0), 则b-a+2022的值是 .
13. 把抛物线y =x 向左平移 1个单位长度，再向下平移2个单位长度，所得抛物线的解析式为 .
14. 已知二次函数的图象经过点(-1, 0), (1, -8)和(3，0)， 则它的解析式为 .
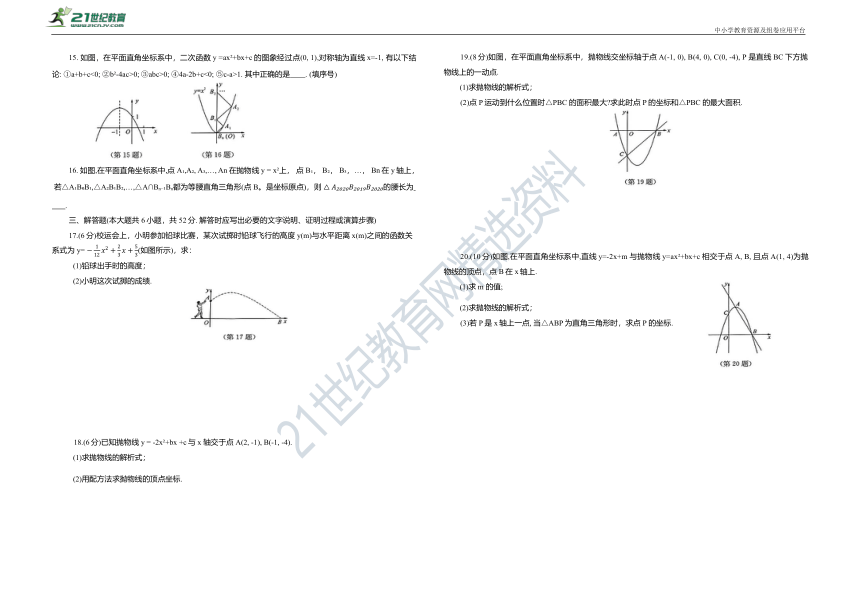
15. 如图，在平面直角坐标系中，二次函数y =ax +bx+c的图象经过点(0, 1),对称轴为直线x=-1, 有以下结论: ①a+b+c<0; ②b -4ac>0; ③abc>0; ④4a-2b+c<0; ⑤c-a>1. 其中正确的是 . (填序号)
16. 如图,在平面直角坐标系中,点A ,A , A ,…, An在抛物线y = x 上， 点 B ， B ， B ，…， Bn在y轴上， 若△A B B ,△A B B ,…,△A∩B B 都为等腰直角三角形(点B。是坐标原点)，则 的腰长为 .
三、解答题(本大题共6小题，共52分. 解答时应写出必要的文字说明、证明过程或演算步骤)
17.(6分)校运会上，小明参加铅球比赛，某次试掷时铅球飞行的高度y(m)与水平距离x(m)之间的函数关系式为 y= (如图所示)，求：
(1)铅球出手时的高度；
(2)小明这次试掷的成绩.
18.(6分)已知抛物线y = -2x +bx +c与 x 轴交于点A(2, -1), B(-1, -4).
(1)求抛物线的解析式；
(2)用配方法求抛物线的顶点坐标.
19.(8分)如图，在平面直角坐标系中，抛物线交坐标轴于点A(-1, 0), B(4, 0), C(0, -4), P 是直线BC下方抛物线上的一动点.
(1)求抛物线的解析式；
(2)点 P 运动到什么位置时△PBC 的面积最大 求此时点P 的坐标和△PBC 的最大面积.
20.(10分)如图,在平面直角坐标系中,直线y=-2x+m 与抛物线y=ax +bx+c相交于点A, B, 且点A(1, 4)为抛物线的顶点，点B在x轴上.
(1)求m 的值;
(2)求抛物线的解析式；
(3)若 P 是x轴上一点, 当△ABP为直角三角形时，求点 P 的坐标.
21.(10分)如图，在平面直角坐标系中，抛物线 +2)(x-m)(m>0)与x轴交于点B,C(点B在点 C 的左侧),与y轴交于点E, 且经过点P(2, 2).
(1)求抛物线的解析式；
(2)在(1)的条件下,求△BCE 的面积;
(3)在(1)的条件下，在抛物线的对称轴上找一点 H，使EH+BH 的值最小,并求出点 H 的坐标.
22.(12分)如图，在平面直角坐标系中，抛物线y=x +bx+c经过点A(-1, 0), B(0, -2), 并与x轴交于另一点C，M是抛物线对称轴l上任意一点(点M，B，C不在同一直线上).
(1)求抛物线的解析式；
(2)在抛物线上找一点 P，使得以M， C，B， P为顶点的四边形为平行四边形，并求出点 P的坐标.
中小学教育资源及组卷应用平台
专题训练二 二次函数(一)
1. A 2. D 3. A 4. B 5. D 6. C 7. B 8. A 9. D 10. C11.> 12.2027 13. y=(x+1) -2 14. y=2x -4x-615.①②③⑤16.2020
17.(1)当x=0时, ∴铅球出手时的高度为
(2)把y=0代入解析式,得
解得x =10, x =-2((舍去),
故小明这次试掷的成绩是 10m.
18. (1)把A(2, -1), B(-1, -4)代入y=-2x +bx+c,
得 解得
故该抛物线的解析式为y =-2x +3x+1.
∴抛物线的顶点坐标是
19.(1)设抛物线的解析式为y=ax +bx+c,把点A,B,C的坐标代入，
得 解得
∴抛物线的解析式为y= x -3x-4.
(2)过点 P 作 PE⊥x轴于点E,交直线 BC于点F, 如图.
∵点 P在抛物线上，
∴设P(t, t -3t-4).
∵B(4, 0), C(0, -4),
∴直线 BC 的解析式为y=x-4,
∴F(t, t-4),
∴PF=(t-4)-(t -3t-4)=-t +4t,
∴当t=2时, S△PBC的最大值为8,此时t -3t-4= -6,
∴当点P的坐标为(2, -6)时,△PBC 的面积最大,最大面积为8.
20.(1)将点 A 的坐标代入y=-2x+m, 得4=-2+m, 解得m =6.
(2)由(1)得 y=-2x+6, 令y=0, 得x=3, ∴点B(3, 0).∵点A(1,4)为抛物线的顶点,
∴设抛物线的解析式为y=a(x-1) +4,
将点B的坐标代入上式，得0=a(3-1) +4,解得a=-1,
∴抛物线的解析式为y=-(x-1) +4=-x +2x+3.
(3)①当∠BAP=90°时, 直线AB 的解析式为y=-2x+6,
∴直线PA的解析式中k的值为-
设直线 PA 的解析式为
将点A 的坐标代入上式，得 解得
∴直线 PA的解析式为
当y=0时, x=-7, 即点 P(-7, 0);
②当∠APB=90°时, 点 P(1, 0).
综上,点 P 的坐标为(-7, 0)或(1, 0).
21. (1)将点 P 的坐标代入抛物线的解析式，
得 解得 m=4,
∴抛物线的解析式为
(2)令y=0, 则 解得x=-2或x=4,
∴B(-2, 0), C(4, 0), ∴BC=4-(-2)=6.
令x=0, 则y=2, ∴OE=2,
(3)如图，作点 E 关于抛物线对称轴的对称点F，连接 BF 交抛物线的对称轴于点H, 连接 EH. 此时 EH +BH =FH+HB=FB, 值最小.
∴抛物线的对称轴为直线x=1.
∴点F(2, 2).
设直线 BF 的解析式为y=kx+b,将点B,F 的坐标代入,得 解得
∴直线 BF 的解析式为
当x=1时, ∴点
22.(1)把A(-1, 0), B(0, -2)代入抛物线y=x +bx+c,得 解得
∴抛物线的解析式为y =x -x -2.
∴对称轴是直线
①如图①，当四边形 PCBM是平行四边形时,MP∥BC,且MP=BC,
∵点B向右平移 个单位长度到点M横坐标位置，
∴点C向右平移 个单位长度到点 P横坐标位置，
∵点C(2, 0), ∴点P的横坐标为 当 时; ∴点
②如图②，当四边形 PMCB 是平行四边形时，
∵点C向左平移2个单位长度到点 B 横坐标位置，
∴点M向左平移2个单位长度到点 P 横坐标位置，
∴点P 的横坐标为
当 时,
∴点
③当BC为对角线时，
∵点M 的横坐标为 ,
∴点P的横坐标为 ,
当 时, ∴点
综上所述， 满足条件的点P 的坐标为 或 或