人教版六年级下册数学正比例和反比例课件(共33张PPT)
文档属性
| 名称 | 人教版六年级下册数学正比例和反比例课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-13 06:17:11 | ||
图片预览











文档简介
(共33张PPT)
正比例与反比例比较
正比例
两 种 ( 相关联 )的量, 一种
量 ( 变化 ),另 一种量也随着
( 变化 ),如果这两种量中相对应的两 个数的( 比值 )一定,这两种量就叫
做成正比例的量,它们的关系叫做 ( 正比例关系 )。
y x =k
( 一 定)
反比例
两 种 ( 相 关 联 ) 的 量 , 一 种
量 ( 变 化 ) , 另 一 种 量 也 随 着
( 变 化 ) , 如 果 这 两 种 量 中 相 对 应 的 两
个数的( 乘积) 一 定,这两种量就叫
做成反比例的量,它们的关系叫做
( 反比例关系 )。
x x y=R ( 一 定 )
正比例
反比例
相同点 都是两种相关联的量, 一种量随着另一种量变化。
不同点 1.变化的方向相同, 一种量扩大或缩小, 另一种量也扩大或缩 小 。
1.变化的方向相反,
一种量扩大( 缩小), 另一种量反而缩小
(扩大)。
2.相对应的每两个数 的比值(商)是一定的 。。
2.相对应的每两个数
的乘积是一定的 。
3 . 关系式: y/x=k(一定)
3 . 关系式:
x×y=k(一定)
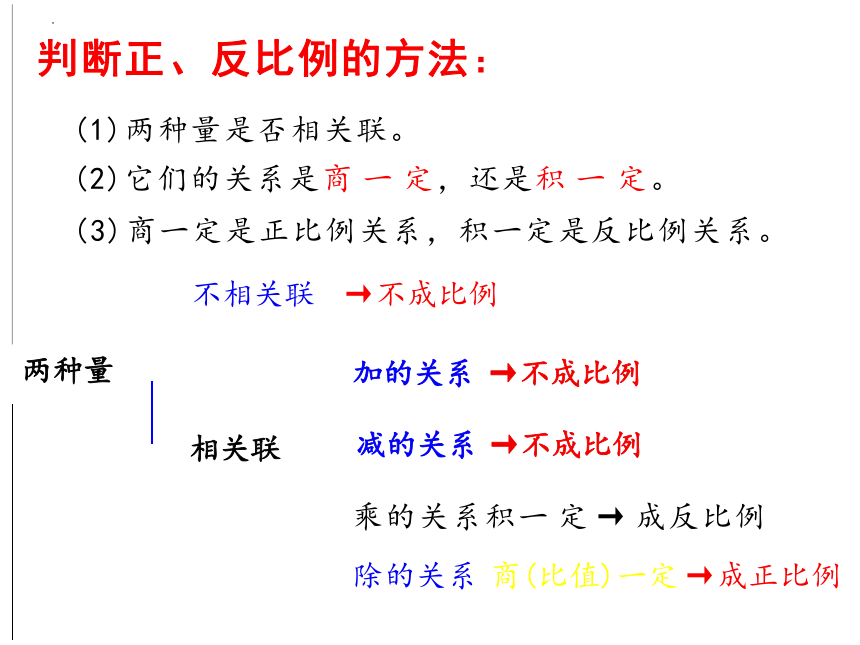
不相关联 →不成比例
加的关系 →不成比例
相关联 减的关系 →不成比例
乘的关系积一 定 → 成反比例
除的关系 商(比值)一定 →成正比例
判断正、反比例的方法:
(1)两种量是否相关联。
(2)它们的关系是商 一 定,还是积 一 定。
(3)商一定是正比例关系,积一定是反比例关系。
两种量
当路程一定时,速度和时间成(
当速度一定时,路程和时间成(
当时间一定时,路程和速度成(
路程、速度和时间这三个量中每两个量
之间有什么样的比例关系
反比例
关系
正比例 关系
正比例
关系
思考
).
).
判断单价、数量和总价中一种量一定,
另外两个量成什么比例关系。为什么
单价一定,数量和总价 正 比 例
总价一定,数量和单价 反 比 例
数量一定,总价和单价 正比例
做一做
易错易混题(一)
1 圆的周长和半径.( 正 比例 )
C=2πr 圆 长=2π ( 一 定 )
2 圆的周长和直径. (正比例)
C=dπ 圆的周长=π( 一 定)
3 圆的面积和半径. (不成比例)
S=πr 圆 积=πr (不一定)
半径
的面
半径
的周
直径
易错易混题(二)
1 正方形的周长和边长. ( 正 比 例 )
边长 =4 ( 一 定)
2 正方形的面积和边长.( 不 成 比 例) 正方形的面积=边长 (不一定)
3 正方体的体积和它的棱长.
正方 积 =棱长×6(不一定)(不成比例)
4 正方体一个面的面积和它的表面积.
长
的体
棱
体
=6 ( 一 定) ( 正 比 例 )
一个面的面积
正方体的表面积
正方形的周长
我能村、 辨一辨
(1)收入一定,支出和结余成正比例 (X )
(2)出米率一定,稻谷的重量和大米的重量成正
比例。( √
(3)圆柱的侧面积一定,它的底面周长和高
成正比例。( X )
(4)三角形的面积一定,它的底和高成反比例。
( √ )
(5)小明从家步行到学校,步行的速度和所
需的时间成反比例。( √ )
A. 正比例 B.反比例 C.不成比例
1. 小明的身高和体重。 ( C )
P .圆锥的体积一定,底面积和高 (B )
3. 正方体的表面积和其中一个面的面积 (A )
4.所行路程一定,车轮周长和车轮转数 (B ) 5. 甲数是乙数的4/5,那么甲数与乙数 ( A ) 6.长方形的周长一定,长与宽。(C)
我有一双火眼金睛
判断下面两个量是否成比例关系。若成,
成什么比例关系。
1、 一条绳子的长度一定,剪去的部分和剩下的部 分。 ( 不成比例 )
2 、同时同地,竹竿高和影长。 ( 成正比例 )
3 、如果ab=8,a 和b 。 ( 成反比例 )
4 、圆的直径和它的周长。 ( 成正比例 )
5 、圆的直径和它的面积。 ( 不成比例)
6 、长方体的体积一定,底面积和高。 (成反比例)
若x和y是两种相关联的量,判断 它们是否成比例,成什么比例
(1)若x = 4 y,(x,y均不为0)
则x和y成( 正 )比例
(2)若 X (, 八x; y 不为
0) 则x和y, 成( 正 )比例.
若x和y是两种相关联的量,判断
它们是否成比例,成什么比例
(3)若 则x和y成(反)比例。
(4)若x:4=5:y,则x和y成( 反) 比例。
( 5)若x=y+5, 则x和y (不成)比例。
根据下列等式判断x和y是否成比例,成什么比例 (1)2xy=8 ( 反比例 )
(3)x+y=5
( 正比例)
( 不成比例)
(4)3x=y ( 正比例)
(5) (6) x 3 二 4 y X 二 y 65 一
( 反比例 )
( 正比例 )
3、 车轮的周长、转数和行驶的路程三者之间有什么比
例关系
车轮的周长×转数=行驶的路程(一 定)反比例
= 转 数 ( 一 定 ) 正比例
= 车轮的周长( 一 定) 正比例
行驶的路程
车轮的周长
行驶的路程
转数
4、 圆的周长与直径成什么比例 圆的周长与半径成什
么比例 圆的面积与半径成什么比例
圆 的 周 长
= 圆 周 率 ( 一 定 ) 正 比 例
直 径
=圆周率×2(一 定) 正比例
圆 积 = 半径×圆周率(不 一 定) 不成比例
径
面
半
的
圆的周长
半径
5 、假设两个圆的半径分别是3cm 和 5cm。
两个圆半 径的比:
两个圆直 径的比:
两个圆周 长的比:
两个圆面 积的比:
结论:两个圆半径的比=两个圆直径的比=两个圆周长的比
两个圆面积的比=两个圆半径的平方的比
正、反比例应用题:
用比例解问题的过程可以归纳为以下几
个步骤 :
(1)设要求的问题为x;
(2) 判断题目中哪个量是一定的 另外两种
量成正比例关系( 除的关系)还是成反比例关系 ( 乘的关系)
(3)列比例式;
(4)解比例,验算,作答。
1、 王叔叔开车从甲地到乙地,前2小时行了
100km 。 照这样的速度,从甲地到乙地一共 要用3小时,甲乙两地相距多远
解:设甲乙两地相距X 千米。
x=150
答:甲乙两地相距150km。
2x=100×3
2 、 王叔叔开车从甲地到乙地一共用了3小时,每小时
行50km。 返回时每小时行60km, 返回时用了多长时
间
解:设返回时用了X 小时。
60×=50×3
x=2.5
答:返回时用了2.5小时。
3 、用一台打字机打字,6小时打36页, 照这样计算,
如果再打4小时, 一共可以打字多少页
解:设一共可以打字X 页。
x=60
答: 一共可以打字60页。
6x=10×36
4、 工人们安装一批电线杆,每天安装12根,30天可 以完成。如果每天多安装6根,几天能够完成
解:设X 天可以完成。
(12+6)x=12×30
18x=12×30
x=20
答:20天可以完成。
堂练
课习
(1 )写出李阿姨平时和节日期间
剪纸张数及相应工作时间的比。
平时:72:6 节日期间:96:8
(2)上面两个比能组成比例吗 为什么
(3)如果李阿姨要剪出120张剪纸,需要多少小时
4 李阿姨是剪纸艺人。平时李阿 姨每天工作6小时,剪出72张 纸;节日期间,李阿姨每天要 工作8小时,能剪出96张剪纸。
1. (1)把1g药放入100g水中,药和药水的比是1:101。
(2) :6的比值是 。如果前项乘3,要使比值不 变,后项应该(乘3)。
(3)化简比。
(4)如果a×3=b×5, 如果a:4=0.2:7,
0.12:56
那么a:b=(5):(3 那么
10
9
5
6
3. 下面各题中的两种量是不是成比例 如果成比例,成什么 比例关系
(1)全班人数一定,出勤人数和缺勤人数。
(2)分数的大小一定,它的分子和分母。
(3)三角形的面积一定,它的底和高。
(4)正方体一个面的面积和它的表面积。
两 种 植 益 的 的 珠 因 的 革 的 景
体
的 们 营 。 侧 为
一定T, 和一定;母所以出勤人 不
和 分 成 生 化 例 。 + T
正 从 数 面 热 薪 农 数 是
KR开N 定 天 样 书 ; 出 大
人数+缺勤数积全班人数
数覆缺勤效数而载 农 份 子
它的一个面的面积成正比例。
2. 写出两个比值都是3的比,并组成比例。
4. 水是由氢和氧按1:8的质量比化合而成的。5.4kg 的水
含氢和氧各多少
同样,设氧有y千克。
9y=8×5.4
答:氢有0.6kg, 氧有4.8kg。
解:设氢有X 千克。
9x=1×5.4
y =4.8
x=0.6
5. 学校会议室用方砖铺地。用8dm 的方砖铺,需要350块:
如果改用10dm 的方砖铺,需要多少块
解:设需要X 块。
10×=350×8
×=280
答:需要280块。
懒惰厌学难成器;
勤奋博学出状元。
正比例与反比例比较
正比例
两 种 ( 相关联 )的量, 一种
量 ( 变化 ),另 一种量也随着
( 变化 ),如果这两种量中相对应的两 个数的( 比值 )一定,这两种量就叫
做成正比例的量,它们的关系叫做 ( 正比例关系 )。
y x =k
( 一 定)
反比例
两 种 ( 相 关 联 ) 的 量 , 一 种
量 ( 变 化 ) , 另 一 种 量 也 随 着
( 变 化 ) , 如 果 这 两 种 量 中 相 对 应 的 两
个数的( 乘积) 一 定,这两种量就叫
做成反比例的量,它们的关系叫做
( 反比例关系 )。
x x y=R ( 一 定 )
正比例
反比例
相同点 都是两种相关联的量, 一种量随着另一种量变化。
不同点 1.变化的方向相同, 一种量扩大或缩小, 另一种量也扩大或缩 小 。
1.变化的方向相反,
一种量扩大( 缩小), 另一种量反而缩小
(扩大)。
2.相对应的每两个数 的比值(商)是一定的 。。
2.相对应的每两个数
的乘积是一定的 。
3 . 关系式: y/x=k(一定)
3 . 关系式:
x×y=k(一定)
不相关联 →不成比例
加的关系 →不成比例
相关联 减的关系 →不成比例
乘的关系积一 定 → 成反比例
除的关系 商(比值)一定 →成正比例
判断正、反比例的方法:
(1)两种量是否相关联。
(2)它们的关系是商 一 定,还是积 一 定。
(3)商一定是正比例关系,积一定是反比例关系。
两种量
当路程一定时,速度和时间成(
当速度一定时,路程和时间成(
当时间一定时,路程和速度成(
路程、速度和时间这三个量中每两个量
之间有什么样的比例关系
反比例
关系
正比例 关系
正比例
关系
思考
).
).
判断单价、数量和总价中一种量一定,
另外两个量成什么比例关系。为什么
单价一定,数量和总价 正 比 例
总价一定,数量和单价 反 比 例
数量一定,总价和单价 正比例
做一做
易错易混题(一)
1 圆的周长和半径.( 正 比例 )
C=2πr 圆 长=2π ( 一 定 )
2 圆的周长和直径. (正比例)
C=dπ 圆的周长=π( 一 定)
3 圆的面积和半径. (不成比例)
S=πr 圆 积=πr (不一定)
半径
的面
半径
的周
直径
易错易混题(二)
1 正方形的周长和边长. ( 正 比 例 )
边长 =4 ( 一 定)
2 正方形的面积和边长.( 不 成 比 例) 正方形的面积=边长 (不一定)
3 正方体的体积和它的棱长.
正方 积 =棱长×6(不一定)(不成比例)
4 正方体一个面的面积和它的表面积.
长
的体
棱
体
=6 ( 一 定) ( 正 比 例 )
一个面的面积
正方体的表面积
正方形的周长
我能村、 辨一辨
(1)收入一定,支出和结余成正比例 (X )
(2)出米率一定,稻谷的重量和大米的重量成正
比例。( √
(3)圆柱的侧面积一定,它的底面周长和高
成正比例。( X )
(4)三角形的面积一定,它的底和高成反比例。
( √ )
(5)小明从家步行到学校,步行的速度和所
需的时间成反比例。( √ )
A. 正比例 B.反比例 C.不成比例
1. 小明的身高和体重。 ( C )
P .圆锥的体积一定,底面积和高 (B )
3. 正方体的表面积和其中一个面的面积 (A )
4.所行路程一定,车轮周长和车轮转数 (B ) 5. 甲数是乙数的4/5,那么甲数与乙数 ( A ) 6.长方形的周长一定,长与宽。(C)
我有一双火眼金睛
判断下面两个量是否成比例关系。若成,
成什么比例关系。
1、 一条绳子的长度一定,剪去的部分和剩下的部 分。 ( 不成比例 )
2 、同时同地,竹竿高和影长。 ( 成正比例 )
3 、如果ab=8,a 和b 。 ( 成反比例 )
4 、圆的直径和它的周长。 ( 成正比例 )
5 、圆的直径和它的面积。 ( 不成比例)
6 、长方体的体积一定,底面积和高。 (成反比例)
若x和y是两种相关联的量,判断 它们是否成比例,成什么比例
(1)若x = 4 y,(x,y均不为0)
则x和y成( 正 )比例
(2)若 X (, 八x; y 不为
0) 则x和y, 成( 正 )比例.
若x和y是两种相关联的量,判断
它们是否成比例,成什么比例
(3)若 则x和y成(反)比例。
(4)若x:4=5:y,则x和y成( 反) 比例。
( 5)若x=y+5, 则x和y (不成)比例。
根据下列等式判断x和y是否成比例,成什么比例 (1)2xy=8 ( 反比例 )
(3)x+y=5
( 正比例)
( 不成比例)
(4)3x=y ( 正比例)
(5) (6) x 3 二 4 y X 二 y 65 一
( 反比例 )
( 正比例 )
3、 车轮的周长、转数和行驶的路程三者之间有什么比
例关系
车轮的周长×转数=行驶的路程(一 定)反比例
= 转 数 ( 一 定 ) 正比例
= 车轮的周长( 一 定) 正比例
行驶的路程
车轮的周长
行驶的路程
转数
4、 圆的周长与直径成什么比例 圆的周长与半径成什
么比例 圆的面积与半径成什么比例
圆 的 周 长
= 圆 周 率 ( 一 定 ) 正 比 例
直 径
=圆周率×2(一 定) 正比例
圆 积 = 半径×圆周率(不 一 定) 不成比例
径
面
半
的
圆的周长
半径
5 、假设两个圆的半径分别是3cm 和 5cm。
两个圆半 径的比:
两个圆直 径的比:
两个圆周 长的比:
两个圆面 积的比:
结论:两个圆半径的比=两个圆直径的比=两个圆周长的比
两个圆面积的比=两个圆半径的平方的比
正、反比例应用题:
用比例解问题的过程可以归纳为以下几
个步骤 :
(1)设要求的问题为x;
(2) 判断题目中哪个量是一定的 另外两种
量成正比例关系( 除的关系)还是成反比例关系 ( 乘的关系)
(3)列比例式;
(4)解比例,验算,作答。
1、 王叔叔开车从甲地到乙地,前2小时行了
100km 。 照这样的速度,从甲地到乙地一共 要用3小时,甲乙两地相距多远
解:设甲乙两地相距X 千米。
x=150
答:甲乙两地相距150km。
2x=100×3
2 、 王叔叔开车从甲地到乙地一共用了3小时,每小时
行50km。 返回时每小时行60km, 返回时用了多长时
间
解:设返回时用了X 小时。
60×=50×3
x=2.5
答:返回时用了2.5小时。
3 、用一台打字机打字,6小时打36页, 照这样计算,
如果再打4小时, 一共可以打字多少页
解:设一共可以打字X 页。
x=60
答: 一共可以打字60页。
6x=10×36
4、 工人们安装一批电线杆,每天安装12根,30天可 以完成。如果每天多安装6根,几天能够完成
解:设X 天可以完成。
(12+6)x=12×30
18x=12×30
x=20
答:20天可以完成。
堂练
课习
(1 )写出李阿姨平时和节日期间
剪纸张数及相应工作时间的比。
平时:72:6 节日期间:96:8
(2)上面两个比能组成比例吗 为什么
(3)如果李阿姨要剪出120张剪纸,需要多少小时
4 李阿姨是剪纸艺人。平时李阿 姨每天工作6小时,剪出72张 纸;节日期间,李阿姨每天要 工作8小时,能剪出96张剪纸。
1. (1)把1g药放入100g水中,药和药水的比是1:101。
(2) :6的比值是 。如果前项乘3,要使比值不 变,后项应该(乘3)。
(3)化简比。
(4)如果a×3=b×5, 如果a:4=0.2:7,
0.12:56
那么a:b=(5):(3 那么
10
9
5
6
3. 下面各题中的两种量是不是成比例 如果成比例,成什么 比例关系
(1)全班人数一定,出勤人数和缺勤人数。
(2)分数的大小一定,它的分子和分母。
(3)三角形的面积一定,它的底和高。
(4)正方体一个面的面积和它的表面积。
两 种 植 益 的 的 珠 因 的 革 的 景
体
的 们 营 。 侧 为
一定T, 和一定;母所以出勤人 不
和 分 成 生 化 例 。 + T
正 从 数 面 热 薪 农 数 是
KR开N 定 天 样 书 ; 出 大
人数+缺勤数积全班人数
数覆缺勤效数而载 农 份 子
它的一个面的面积成正比例。
2. 写出两个比值都是3的比,并组成比例。
4. 水是由氢和氧按1:8的质量比化合而成的。5.4kg 的水
含氢和氧各多少
同样,设氧有y千克。
9y=8×5.4
答:氢有0.6kg, 氧有4.8kg。
解:设氢有X 千克。
9x=1×5.4
y =4.8
x=0.6
5. 学校会议室用方砖铺地。用8dm 的方砖铺,需要350块:
如果改用10dm 的方砖铺,需要多少块
解:设需要X 块。
10×=350×8
×=280
答:需要280块。
懒惰厌学难成器;
勤奋博学出状元。
