初中数学人教版八上13.4课题学习 最短路径问题 习题(含解析)
文档属性
| 名称 | 初中数学人教版八上13.4课题学习 最短路径问题 习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 459.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-13 23:39:56 | ||
图片预览



文档简介
13.4课题学习 最短路径和
1.如图,△ABC中,AB=5,AC=9,BC=10,EF垂直平分BC,点P为直线EF上的任一点,则△ABP周长的最小值是( )
A.10 B.14 C.15 D.19
2. 如图,分别是线段MC,MD的垂直平分线,MC=7 cm,MD=5 cm,CD=10 cm,一只小蚂蚁从点M出发爬到边上任意一点E,再爬到边上任意一点F,然后爬回M点,则小蚂蚁爬行的最短路径为( )
A.12 cm B.10 cm C.7 cm D.5 cm
3. 如图,直线m表示一条河,M,N表示两个村庄,欲在m上的某处修建一个给水站,向两个村庄供水,现有如图所示的四种铺设管道的方案,图中实线表示铺设的管道,则所需管道最短的方案是( )
A. B.
C. D.
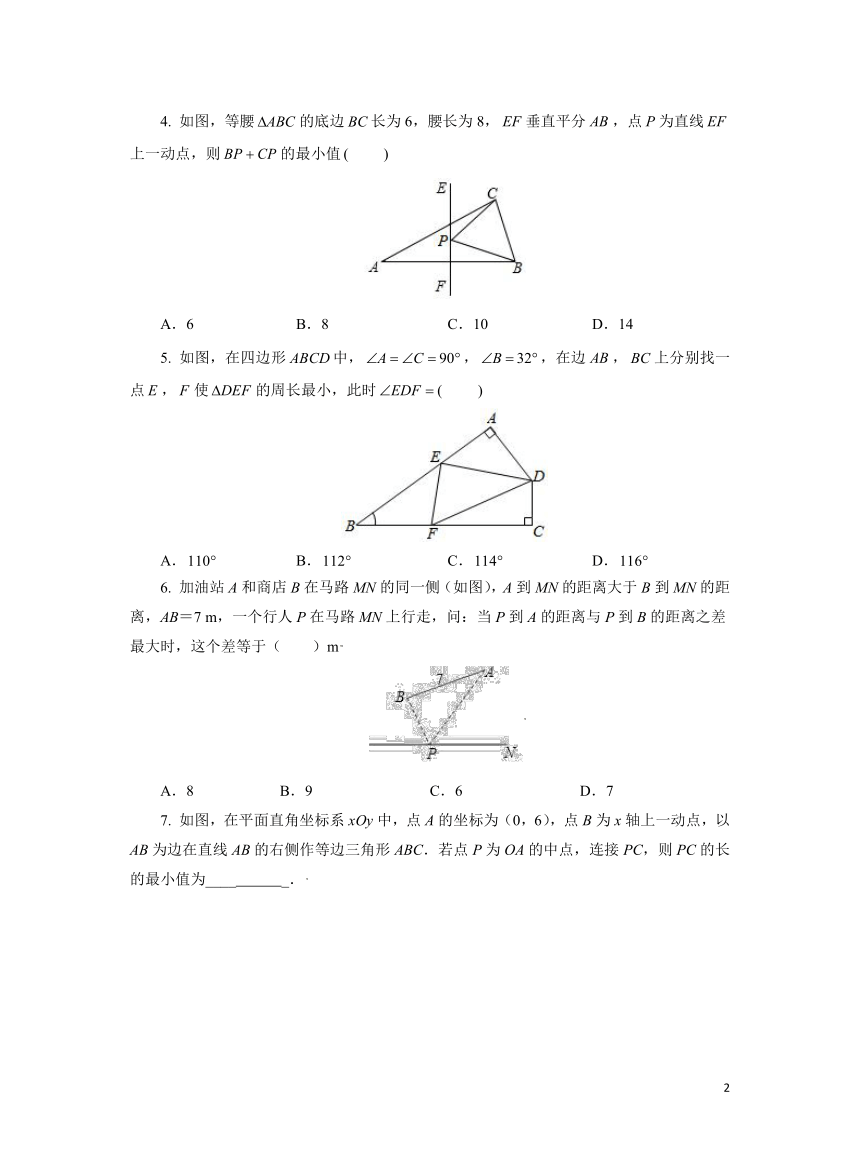
4. 如图,等腰的底边长为6,腰长为8,垂直平分,点为直线上一动点,则的最小值
A.6 B.8 C.10 D.14
5. 如图,在四边形中,,,在边,上分别找一点,使的周长最小,此时
A. B. C. D.
6. 加油站A和商店B在马路MN的同一侧(如图),A到MN的距离大于B到MN的距离,AB=7 m,一个行人P在马路MN上行走,问:当P到A的距离与P到B的距离之差最大时,这个差等于( )m
A.8 B.9 C.6 D.7
7. 如图,在平面直角坐标系xOy中,点A的坐标为(0,6),点B为x轴上一动点,以AB为边在直线AB的右侧作等边三角形ABC.若点P为OA的中点,连接PC,则PC的长的最小值为____ _.
8. 如图,在Rt△ABC中,,,,是△ABC的角平分线,点,点分别是,边上的动点,点在上,且BM=1,求的最小值.
9. 如图,在△ABC中,∠ACB=90°,以AC为底边在△ABC外作等腰△ACD,过点D作∠ADC的平分线分别交AB,AC于点E,F.若AC=12,BC=5,△ABC的周长为30,点P是直线DE上的一个动点,则△PBC周长的最小值是多少?.
10.如图是某风景区的旅游线示意图,其中B、C、D为风景点,E为两条路的交叉点,图中数据为相应两点间的路程(单位:km),一学生从A处出发,以2 km/h的速度步行游览,每个景点的逗留时间为0.5 h.
(1)当他沿着路线A→D→C→E→A游览回到A处时,共用了3 h,求CE的长;
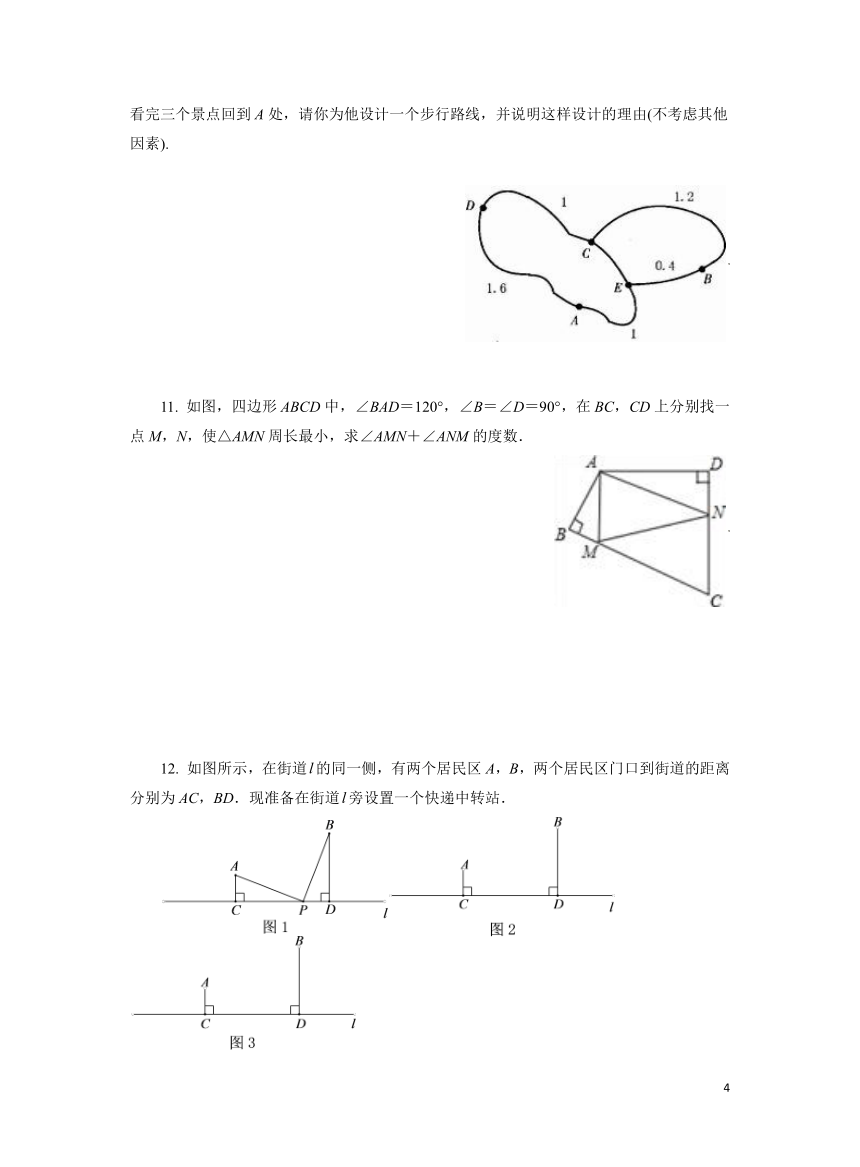
(2)若此学生打算从A处出发后,步行速度与在景点逗留的时间不变,且在最短时间内看完三个景点回到A处,请你为他设计一个步行路线,并说明这样设计的理由(不考虑其他因素).
11. 如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小,求∠AMN+∠ANM的度数.
12. 如图所示,在街道的同一侧,有两个居民区A,B,两个居民区门口到街道的距离分别为AC,BD.现准备在街道旁设置一个快递中转站.
(1)如果设置的快递中转站到A,B两个小区的距离相等,如图1,当∠A=∠BPD时,请说明AC+BD=CD的理由;
(2)如果设置的快递中转站到A,B两个小区的距离之和最短,请在图2中作出点P的位置,连接AP,BP,直接写出此时∠PAC与∠PBD的数量关系;
(3)为了能错峰进行取送快递,决定设置的快递中转站到A,B两个小区的距离之差最大,请在图3中作出点P的位置,连接AP,BP,直接写出此时∠PAC与∠PBD的数量关系.
参考答案
1.B
解析:连接PC,如图所示:
∵EF垂直平分BC,
∴,
∵,
∴的周长为,
若使周长为最小,则需满足为最小,即为最小,
∵,
∴当点A、P、C三点共线时,为最小,即为AC的长,
∴的周长最小值为.
2.B
解析:由题意可知CD与OA的交点为E,与OB的交点为F.
∵OA,OB分别是线段MC,MD的垂直平分线,
∴ME=CE,MF=DF,
∴小蚂蚁爬行的最短路径为ME+EF+FM=CE+EF+FD=CD=10 cm.
3.D
解析:作点M关于直线m的对称点,连接交直线m于P,则P处即为给水站位置.根据“两点之间,线段最短”可排除,B,C选项,可知D选项管道最短.
4.B
解析:连接,
垂直平分,
,
,
当时,值最小,
等腰腰长为8,
,
的最小值为8.
5.D
解析:如图,作点关于的对称点,点关于的对称点,连接,交于,交于,则点,即为所求.
四边形中,,,
,
由轴对称知,,,
在中,
,
,
.
6.D
解析:当A,B,P三点不在同一直线上时,此时三点构成三角形,因为两边AP与BP的差小于第三边AB,所以A,B,P在同一直线上,所以P到A的距离与P到B的距离之差最大,这个差就是AB的长.
7.
解析:如图,以AP为边作等边三角形APE,连接BE,过点E作EF⊥AP于F,
∵点A的坐标为(0,6),
∴OA=6,
∵点P为OA的中点,
∴AP=3,
∵△AEP是等边三角形,EF⊥AP,
∴AF=PF=,AE=AP,∠EAP=∠BAC=60°,
∴∠BAE=∠CAP,
在△ABE和△ACP中,
∴△ABE≌△ACP,
∴BE=PC,
∴当BE有最小值时,PC有最小值,即BE⊥x轴时,BE有最小值,
∴BE的最小值为OF=OP+PF=3+=,
∴PC的最小值为.
8.解:如图所示,作点关于的对称点,连接,则,,
,当,,在同一直线上,且时,的最小值等于垂线段的长,
此时,∵Rt△中,,
∴,
∴的最小值为.
9.解:∵△ACD是以为底边的等腰三角形,平分,
ED垂直平分AC,
∴点与点关于对称,
∴PC=PA,
如图所示,当点与点重合时,,
此时的周长最小,
,,的周长为30,
∴AB=13,
∴△PBC周长的最小值为.
10.解:(1)由题意得CE=2×(3-2×0. 5)-1.6-1-1=0.4(km);
(2)若步行路线为A→D→C→B→E→A(或A→E→B→C→D→A)
则所用时间为(1.6+1+1.2+0.4+1)÷2+3×0.5=4.1 h,
若步行路线为A→D→C→E→B→E→A(或A→E→B→E→C→D→A)
则所用时间为(1.6+1+0.4+0.4×2+1)÷2+3×0.5=3.9 h,
则最短步行路线为A→D→C→E→B→E→A(或A→E→B→E→C→D→A).
11.解:
作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,连接AM,AN,则A′A″即为△AMN的周长最小值.作DA延长线AH.
∵∠DAB=120°,
∴∠HAA′=60°.
∴∠A′+∠A″=∠HAA′=60°.
∵∠A′=∠MAA′,∠NAD=∠A″,且∠A′+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠A′+∠MAA′+∠NAD+∠A″=2(∠A′+∠A″)=2×60°=120°.
12.解:(1)∵ AC,BD分别是点A,B到直线的距离,
∴ ∠ACP=∠BDP=90°,
在△ACP和△PDB中,,
∴ △ACP≌△PDB(AAS),
∴ AC=PD,PC=BD,
∴CD=CP+PD=BD+AC.
(2)如图1所示,∠A=∠B,
理由:由作图知,
AC=,⊥l,
∴∠A=∠,
∵A∥BD,
∴∠=∠B,
∴∠A=∠B.
(3)如图2所示,
∵∠ACD=∠BDC=90°,
∴∠ACD+∠BDC=180°,
∴AC∥BD,
∴∠PAC=∠PBD.
1
1.如图,△ABC中,AB=5,AC=9,BC=10,EF垂直平分BC,点P为直线EF上的任一点,则△ABP周长的最小值是( )
A.10 B.14 C.15 D.19
2. 如图,分别是线段MC,MD的垂直平分线,MC=7 cm,MD=5 cm,CD=10 cm,一只小蚂蚁从点M出发爬到边上任意一点E,再爬到边上任意一点F,然后爬回M点,则小蚂蚁爬行的最短路径为( )
A.12 cm B.10 cm C.7 cm D.5 cm
3. 如图,直线m表示一条河,M,N表示两个村庄,欲在m上的某处修建一个给水站,向两个村庄供水,现有如图所示的四种铺设管道的方案,图中实线表示铺设的管道,则所需管道最短的方案是( )
A. B.
C. D.
4. 如图,等腰的底边长为6,腰长为8,垂直平分,点为直线上一动点,则的最小值
A.6 B.8 C.10 D.14
5. 如图,在四边形中,,,在边,上分别找一点,使的周长最小,此时
A. B. C. D.
6. 加油站A和商店B在马路MN的同一侧(如图),A到MN的距离大于B到MN的距离,AB=7 m,一个行人P在马路MN上行走,问:当P到A的距离与P到B的距离之差最大时,这个差等于( )m
A.8 B.9 C.6 D.7
7. 如图,在平面直角坐标系xOy中,点A的坐标为(0,6),点B为x轴上一动点,以AB为边在直线AB的右侧作等边三角形ABC.若点P为OA的中点,连接PC,则PC的长的最小值为____ _.
8. 如图,在Rt△ABC中,,,,是△ABC的角平分线,点,点分别是,边上的动点,点在上,且BM=1,求的最小值.
9. 如图,在△ABC中,∠ACB=90°,以AC为底边在△ABC外作等腰△ACD,过点D作∠ADC的平分线分别交AB,AC于点E,F.若AC=12,BC=5,△ABC的周长为30,点P是直线DE上的一个动点,则△PBC周长的最小值是多少?.
10.如图是某风景区的旅游线示意图,其中B、C、D为风景点,E为两条路的交叉点,图中数据为相应两点间的路程(单位:km),一学生从A处出发,以2 km/h的速度步行游览,每个景点的逗留时间为0.5 h.
(1)当他沿着路线A→D→C→E→A游览回到A处时,共用了3 h,求CE的长;
(2)若此学生打算从A处出发后,步行速度与在景点逗留的时间不变,且在最短时间内看完三个景点回到A处,请你为他设计一个步行路线,并说明这样设计的理由(不考虑其他因素).
11. 如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小,求∠AMN+∠ANM的度数.
12. 如图所示,在街道的同一侧,有两个居民区A,B,两个居民区门口到街道的距离分别为AC,BD.现准备在街道旁设置一个快递中转站.
(1)如果设置的快递中转站到A,B两个小区的距离相等,如图1,当∠A=∠BPD时,请说明AC+BD=CD的理由;
(2)如果设置的快递中转站到A,B两个小区的距离之和最短,请在图2中作出点P的位置,连接AP,BP,直接写出此时∠PAC与∠PBD的数量关系;
(3)为了能错峰进行取送快递,决定设置的快递中转站到A,B两个小区的距离之差最大,请在图3中作出点P的位置,连接AP,BP,直接写出此时∠PAC与∠PBD的数量关系.
参考答案
1.B
解析:连接PC,如图所示:
∵EF垂直平分BC,
∴,
∵,
∴的周长为,
若使周长为最小,则需满足为最小,即为最小,
∵,
∴当点A、P、C三点共线时,为最小,即为AC的长,
∴的周长最小值为.
2.B
解析:由题意可知CD与OA的交点为E,与OB的交点为F.
∵OA,OB分别是线段MC,MD的垂直平分线,
∴ME=CE,MF=DF,
∴小蚂蚁爬行的最短路径为ME+EF+FM=CE+EF+FD=CD=10 cm.
3.D
解析:作点M关于直线m的对称点,连接交直线m于P,则P处即为给水站位置.根据“两点之间,线段最短”可排除,B,C选项,可知D选项管道最短.
4.B
解析:连接,
垂直平分,
,
,
当时,值最小,
等腰腰长为8,
,
的最小值为8.
5.D
解析:如图,作点关于的对称点,点关于的对称点,连接,交于,交于,则点,即为所求.
四边形中,,,
,
由轴对称知,,,
在中,
,
,
.
6.D
解析:当A,B,P三点不在同一直线上时,此时三点构成三角形,因为两边AP与BP的差小于第三边AB,所以A,B,P在同一直线上,所以P到A的距离与P到B的距离之差最大,这个差就是AB的长.
7.
解析:如图,以AP为边作等边三角形APE,连接BE,过点E作EF⊥AP于F,
∵点A的坐标为(0,6),
∴OA=6,
∵点P为OA的中点,
∴AP=3,
∵△AEP是等边三角形,EF⊥AP,
∴AF=PF=,AE=AP,∠EAP=∠BAC=60°,
∴∠BAE=∠CAP,
在△ABE和△ACP中,
∴△ABE≌△ACP,
∴BE=PC,
∴当BE有最小值时,PC有最小值,即BE⊥x轴时,BE有最小值,
∴BE的最小值为OF=OP+PF=3+=,
∴PC的最小值为.
8.解:如图所示,作点关于的对称点,连接,则,,
,当,,在同一直线上,且时,的最小值等于垂线段的长,
此时,∵Rt△中,,
∴,
∴的最小值为.
9.解:∵△ACD是以为底边的等腰三角形,平分,
ED垂直平分AC,
∴点与点关于对称,
∴PC=PA,
如图所示,当点与点重合时,,
此时的周长最小,
,,的周长为30,
∴AB=13,
∴△PBC周长的最小值为.
10.解:(1)由题意得CE=2×(3-2×0. 5)-1.6-1-1=0.4(km);
(2)若步行路线为A→D→C→B→E→A(或A→E→B→C→D→A)
则所用时间为(1.6+1+1.2+0.4+1)÷2+3×0.5=4.1 h,
若步行路线为A→D→C→E→B→E→A(或A→E→B→E→C→D→A)
则所用时间为(1.6+1+0.4+0.4×2+1)÷2+3×0.5=3.9 h,
则最短步行路线为A→D→C→E→B→E→A(或A→E→B→E→C→D→A).
11.解:
作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,连接AM,AN,则A′A″即为△AMN的周长最小值.作DA延长线AH.
∵∠DAB=120°,
∴∠HAA′=60°.
∴∠A′+∠A″=∠HAA′=60°.
∵∠A′=∠MAA′,∠NAD=∠A″,且∠A′+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠A′+∠MAA′+∠NAD+∠A″=2(∠A′+∠A″)=2×60°=120°.
12.解:(1)∵ AC,BD分别是点A,B到直线的距离,
∴ ∠ACP=∠BDP=90°,
在△ACP和△PDB中,,
∴ △ACP≌△PDB(AAS),
∴ AC=PD,PC=BD,
∴CD=CP+PD=BD+AC.
(2)如图1所示,∠A=∠B,
理由:由作图知,
AC=,⊥l,
∴∠A=∠,
∵A∥BD,
∴∠=∠B,
∴∠A=∠B.
(3)如图2所示,
∵∠ACD=∠BDC=90°,
∴∠ACD+∠BDC=180°,
∴AC∥BD,
∴∠PAC=∠PBD.
1
