初中数学人教版八上14.2.1平方差公式 习题(含解析)
文档属性
| 名称 | 初中数学人教版八上14.2.1平方差公式 习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 99.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 12:22:39 | ||
图片预览



文档简介
14.2.1 平方差公式
1. 下列各式中,不能使用平方差公式计算的是( )
A. B.
C. D.
2.下列各式不能用平方差公式计算的是( )
A. B.
C. D.
3. ( )
A. B.
C. D.
4. 为了应用平方差公式计算,必须先适当变形,下列变形中,正确的是( )
A. B.
C. D.
5. 若三角形的一边长为,该边上的高为,则此三角形的面积是( )
A. B. C. D.
6. 了美化城市,经统一规划,将一正方形草坪的南北方向增加3 m,东西方向缩短3 m,则改造后的长方形草坪面积与原来正方形草坪面积相比( )
A.增加了6 m2 B.增加了9 m2
C.减少了9 m2 D.保持不变
7.填空:(1)(-2y-1)·( )=1-4y2;(2)(5a-b)·( )=25a2-b2.
8. 计算: .
9.方程的解是 .
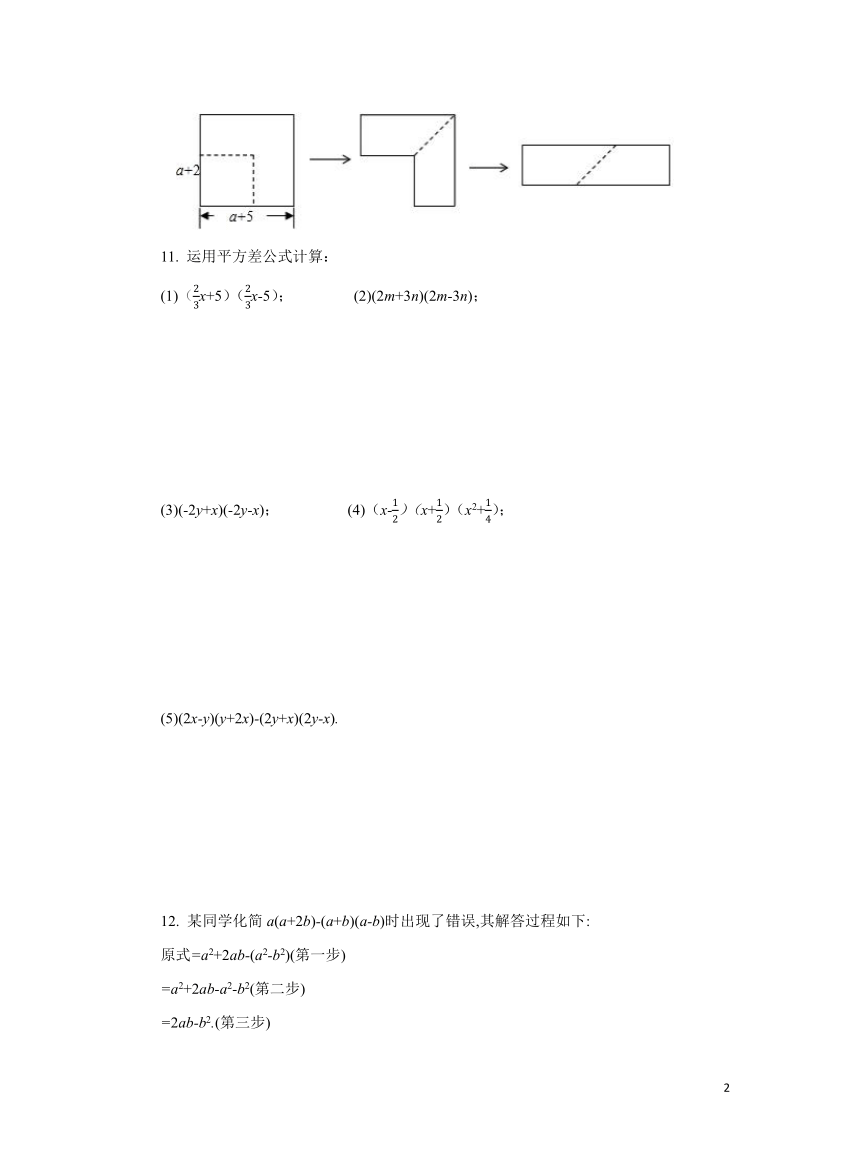
10.如图,从边长为的正方形纸片中剪去一个边长为的正方形(),剩余部分沿虚线又剪拼成一个长方形(不重叠无缝隙),则长方形的面积为________.
11. 运用平方差公式计算:
(1)(x+5)(x-5); (2)(2m+3n)(2m-3n);
(3)(-2y+x)(-2y-x); (4)(x-)(x+)(x2+);
(5)(2x-y)(y+2x)-(2y+x)(2y-x).
12. 某同学化简a(a+2b)-(a+b)(a-b)时出现了错误,其解答过程如下:
原式=a2+2ab-(a2-b2)(第一步)
=a2+2ab-a2-b2(第二步)
=2ab-b2.(第三步)
(1)该同学的解答过程从第 步开始出错,错误原因是 ;
(2)写出此题正确的解答过程.
13. 先化简,再求值:
(y+2)(y-2)+y(4-y),其中y=.
14. (探究)如图1,边长为a的大正方形中有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示),通过观察比较图2与图1中的阴影部分面积,可以得到乘法公式 .(用含a,b的等式表示)
(应用)请应用这个公式完成下列各题:
(1)已知4m2=12+n2,2m+n=4,则2m﹣n的值为 .
(2)计算:20192﹣2020×2018.
(拓展)计算:1002﹣992+982﹣972+…+42﹣32+22﹣12.
15.已知x≠1,观察下列各式:
(1-x)(1+x)=1-x2,(1-x)(1+x+x2)=1-x3,(1-x)(1+x+x2+x3)=1-x4.
(1)猜想:(1-x)(1+x+x2+…+xn)= (n为正整数).
(2)计算:
①(1-2)(1+2+22+23+24+25);
②2+22+23+…+2n(n为正整数);
③(x-1)(x199+x198+…+x+1).
(3)通过以上规律,请你进行下面的探索:
①(a-b)(a+b)= ;
②(a-b)(a2+ab+b2)= ;
③(a-b)(a3+a2b+ab2+b3)= .
参考答案
1.A
解析:A.(x+y)( x-y)=-(x+y)(x+y),不能用平方差公式计算,故本选项符合题意;
B.(x y)( x y)= -(x y)(x+y),能用平方差公式计算,故本选项不符合题意;
C.(x y)(y+x)= (x y)(x+y),能用平方差公式计算,故本选项不符合题意;
D.( y+x) (x+y) =( x y) (x+y),能用平方差公式计算.故本选项不符合题意.
2. C
解析:A. ,能用平方差公式进行计算,所以本选项错误;
B. ,能用平方差公式进行计算,所以本选项错误;
C. ,不能用平方差公式进行计算,所以本选项正确;
D. ,能用平方差公式进行计算,所以本选项错误.
3. D
解析:.
4. D
解析:
选项,,不符合平方差公式的结构特征,只有选项是正确的.
5. C
解析:由题意,三角形面积为:
.
6. C
解析:设原来正方形草坪的边长为a m,则其面积为a2 m2,则变化后的长方形草坪的面积为(a+3)(a-3)=(a2-9) m2.故减少了9 m2.
7. (1)2y-1 (2)5a+b
解析:这两小题都可从右边入手,右边都是平方差的形式,所以有:
(1)1-4y2=12-(2y)2=(1+2y)(1-2y)=(-2y-1)(-1+2y)=(-2y-1)(2y-1).
(2)25a2-b2=(5a)2-b2=(5a+b)(5a-b).
8. 1
解析:原式
.
9.
解析:,
,
,
.
10.
解析:根据题意,长方形的面积:
[(a+5)+(a+2)][(a+5)-(a+2)]
=3(2a+7)
=6a+21.
11. 解:(1)=-52=x2-25.
(2)原式=(2m)2-(3n)2=4m2-9n2.
(3)(-2y+x)(-2y-x)=(-2y)2-x2=4y2-x2.
(4)
=
=(x2)2-=x4-.
(5)原式=4x2-y2-(4y2-x2)
=4x2-y2-4y2+x2=5x2-5y2.
12.解:(1)二 去括号法则用错
(2)原式=a2+2ab-(a2-b2)=a2+2ab-a2+b2=2ab+b2.
13.解:原式=y2-4+4y-y2
=4y-4.
当y=时,
原式=4×-4=-3.所以答案为-3.
14.解:探究:图1中阴影部分面积a2﹣b2,图2中阴影部分面积(a+b)(a﹣b),
所以,得到乘法公式(a+b)(a﹣b)=a2﹣b2所以答案为(a+b)(a﹣b)=a2﹣b2.
应用:(1)由4m2=12+n2得,4m2﹣n2=12
∵(2m+n) (2m+n)=4m2﹣n2
∴2m﹣n=3所以答案为3.
(2)20192﹣2020×2018
=20192﹣(2019+1)×(2019﹣1)
=20192﹣(20192﹣1)
=20192﹣20192+1
=1
拓展:1002﹣992+982﹣972+…+42﹣32+22﹣12
=(100+99)×(100﹣99)+(98+97)×(98﹣97)+…+(4+3)×(4﹣3)+(2+1)×(2﹣1)
=100+99+98+97+…+4+3+2+1
=5050
15. 解:(1)1-xn+1
(2)①原式=1-26=1-64=-63.
②原式=2(1+2+22+…+2n-1)
=-2(1-2)(1+2+22+…+2n-1)
=-2(1-2n)=-2+2×2n=2n+1-2.
③原式=-(1-x)(1+x+…+x198+x199)=-(1-x200)=x200-1.
(3)①a2-b2 ②a3-b3 ③a4-b4
1
1. 下列各式中,不能使用平方差公式计算的是( )
A. B.
C. D.
2.下列各式不能用平方差公式计算的是( )
A. B.
C. D.
3. ( )
A. B.
C. D.
4. 为了应用平方差公式计算,必须先适当变形,下列变形中,正确的是( )
A. B.
C. D.
5. 若三角形的一边长为,该边上的高为,则此三角形的面积是( )
A. B. C. D.
6. 了美化城市,经统一规划,将一正方形草坪的南北方向增加3 m,东西方向缩短3 m,则改造后的长方形草坪面积与原来正方形草坪面积相比( )
A.增加了6 m2 B.增加了9 m2
C.减少了9 m2 D.保持不变
7.填空:(1)(-2y-1)·( )=1-4y2;(2)(5a-b)·( )=25a2-b2.
8. 计算: .
9.方程的解是 .
10.如图,从边长为的正方形纸片中剪去一个边长为的正方形(),剩余部分沿虚线又剪拼成一个长方形(不重叠无缝隙),则长方形的面积为________.
11. 运用平方差公式计算:
(1)(x+5)(x-5); (2)(2m+3n)(2m-3n);
(3)(-2y+x)(-2y-x); (4)(x-)(x+)(x2+);
(5)(2x-y)(y+2x)-(2y+x)(2y-x).
12. 某同学化简a(a+2b)-(a+b)(a-b)时出现了错误,其解答过程如下:
原式=a2+2ab-(a2-b2)(第一步)
=a2+2ab-a2-b2(第二步)
=2ab-b2.(第三步)
(1)该同学的解答过程从第 步开始出错,错误原因是 ;
(2)写出此题正确的解答过程.
13. 先化简,再求值:
(y+2)(y-2)+y(4-y),其中y=.
14. (探究)如图1,边长为a的大正方形中有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示),通过观察比较图2与图1中的阴影部分面积,可以得到乘法公式 .(用含a,b的等式表示)
(应用)请应用这个公式完成下列各题:
(1)已知4m2=12+n2,2m+n=4,则2m﹣n的值为 .
(2)计算:20192﹣2020×2018.
(拓展)计算:1002﹣992+982﹣972+…+42﹣32+22﹣12.
15.已知x≠1,观察下列各式:
(1-x)(1+x)=1-x2,(1-x)(1+x+x2)=1-x3,(1-x)(1+x+x2+x3)=1-x4.
(1)猜想:(1-x)(1+x+x2+…+xn)= (n为正整数).
(2)计算:
①(1-2)(1+2+22+23+24+25);
②2+22+23+…+2n(n为正整数);
③(x-1)(x199+x198+…+x+1).
(3)通过以上规律,请你进行下面的探索:
①(a-b)(a+b)= ;
②(a-b)(a2+ab+b2)= ;
③(a-b)(a3+a2b+ab2+b3)= .
参考答案
1.A
解析:A.(x+y)( x-y)=-(x+y)(x+y),不能用平方差公式计算,故本选项符合题意;
B.(x y)( x y)= -(x y)(x+y),能用平方差公式计算,故本选项不符合题意;
C.(x y)(y+x)= (x y)(x+y),能用平方差公式计算,故本选项不符合题意;
D.( y+x) (x+y) =( x y) (x+y),能用平方差公式计算.故本选项不符合题意.
2. C
解析:A. ,能用平方差公式进行计算,所以本选项错误;
B. ,能用平方差公式进行计算,所以本选项错误;
C. ,不能用平方差公式进行计算,所以本选项正确;
D. ,能用平方差公式进行计算,所以本选项错误.
3. D
解析:.
4. D
解析:
选项,,不符合平方差公式的结构特征,只有选项是正确的.
5. C
解析:由题意,三角形面积为:
.
6. C
解析:设原来正方形草坪的边长为a m,则其面积为a2 m2,则变化后的长方形草坪的面积为(a+3)(a-3)=(a2-9) m2.故减少了9 m2.
7. (1)2y-1 (2)5a+b
解析:这两小题都可从右边入手,右边都是平方差的形式,所以有:
(1)1-4y2=12-(2y)2=(1+2y)(1-2y)=(-2y-1)(-1+2y)=(-2y-1)(2y-1).
(2)25a2-b2=(5a)2-b2=(5a+b)(5a-b).
8. 1
解析:原式
.
9.
解析:,
,
,
.
10.
解析:根据题意,长方形的面积:
[(a+5)+(a+2)][(a+5)-(a+2)]
=3(2a+7)
=6a+21.
11. 解:(1)=-52=x2-25.
(2)原式=(2m)2-(3n)2=4m2-9n2.
(3)(-2y+x)(-2y-x)=(-2y)2-x2=4y2-x2.
(4)
=
=(x2)2-=x4-.
(5)原式=4x2-y2-(4y2-x2)
=4x2-y2-4y2+x2=5x2-5y2.
12.解:(1)二 去括号法则用错
(2)原式=a2+2ab-(a2-b2)=a2+2ab-a2+b2=2ab+b2.
13.解:原式=y2-4+4y-y2
=4y-4.
当y=时,
原式=4×-4=-3.所以答案为-3.
14.解:探究:图1中阴影部分面积a2﹣b2,图2中阴影部分面积(a+b)(a﹣b),
所以,得到乘法公式(a+b)(a﹣b)=a2﹣b2所以答案为(a+b)(a﹣b)=a2﹣b2.
应用:(1)由4m2=12+n2得,4m2﹣n2=12
∵(2m+n) (2m+n)=4m2﹣n2
∴2m﹣n=3所以答案为3.
(2)20192﹣2020×2018
=20192﹣(2019+1)×(2019﹣1)
=20192﹣(20192﹣1)
=20192﹣20192+1
=1
拓展:1002﹣992+982﹣972+…+42﹣32+22﹣12
=(100+99)×(100﹣99)+(98+97)×(98﹣97)+…+(4+3)×(4﹣3)+(2+1)×(2﹣1)
=100+99+98+97+…+4+3+2+1
=5050
15. 解:(1)1-xn+1
(2)①原式=1-26=1-64=-63.
②原式=2(1+2+22+…+2n-1)
=-2(1-2)(1+2+22+…+2n-1)
=-2(1-2n)=-2+2×2n=2n+1-2.
③原式=-(1-x)(1+x+…+x198+x199)=-(1-x200)=x200-1.
(3)①a2-b2 ②a3-b3 ③a4-b4
1
