初中数学人教版八上14.3.2公式法 第1课时 习题(含解析)
文档属性
| 名称 | 初中数学人教版八上14.3.2公式法 第1课时 习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 123.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 12:26:13 | ||
图片预览


文档简介
14.3.2公式法 第1课时
1.因式分解:m2﹣4y2=( )
A.(m+2y)(m﹣2y) B.(2m+y)(2m﹣y)
C.(m+2y)(2m﹣y) D.(2m+y)(m﹣2y)
2.下列各式中不能用平方差公式分解的是( )
A. B. C. D.
3.若=8×10×12,则k=( )
A.12 B.10 C.8 D.6
4.下列各式中,能用平方差公式分解因式的是( )
A.x2+4y2 B.﹣x2+4y2 C.x2﹣2y+1 D.﹣x2﹣4y2
5.利用因式分解能说明:257-512能被( )整除.
A.5 B.10 C.22 D.30
6.有一个因式是,则另一个因式为( )
A. B. C. D.
7.当为正整数时,代数式一定是下面哪个数的倍数( )
A.3 B.5 C.7 D.8
8.因式分解:______.
9.把分解因式得_______.
10.若实数a,b满足,则代数式的值为_______________.
11.因式分解:
(1);(2)n2(m-2)+4(2-m).
12. 在日常生活中,如取款、上网需要密码,有一种因式分解法产生密码,例如,当 x=9,y=9 时, x-y=0 ,x+y=18, x2+y2=162,则密码 018162.对于多项式,取 x=10,y=10,用上述方法产生密码是什么?
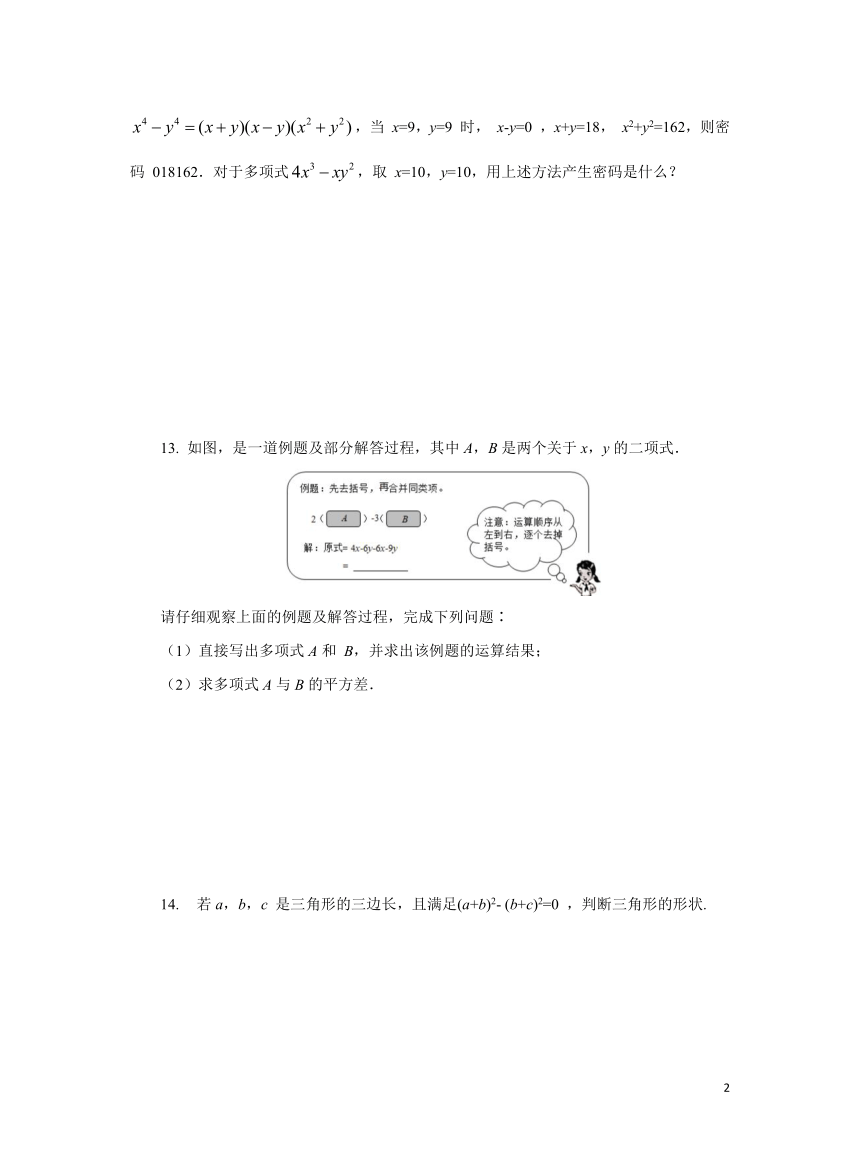
13. 如图,是一道例题及部分解答过程,其中A,B是两个关于x,y的二项式.
请仔细观察上面的例题及解答过程,完成下列问题∶
(1)直接写出多项式A和 B,并求出该例题的运算结果;
(2)求多项式A与B的平方差.
14. 若a,b,c 是三角形的三边长,且满足(a+b)2- (b+c)2=0 ,判断三角形的形状.
15. 已知A=x-y+1,B=x+y+1,C=(x+y)(x-y)+2x.两位同学对x,y分别取了不同的值,求出A,B,C的值各不相同,但A×B-C的值却总是一样的.由此这两位同学得出结论:无论x,y取何值,A×B-C的值不变.你认为这个结论正确吗?请说明理由.
参考答案
1. A
解析:m2-4y2=(m+2y)(m-2y).
2.C
解析:A.=(2+x)(2﹣x),可以用平方差公式分解因式,故此选项错误;
B.=(y+x)(y﹣x),可以用平方差公式分解因式,故此选项错误;
C.,不可以用平方差公式分解因式,故此选项正确;
D.=(1+2x)(1﹣2x),可以用平方差公式分解因式,故此选项错误.
3.B
解析:8×10×12,∴k=10.
4.B
解析:A.两项的符号相同,不能用平方差公式分解因式;
B.是与的平方的差,能用平方差公式分解因式;
C.是三项不能用平方差公式分解因式;
D.两项的符号相同,不能用平方差公式分解因式.
5.D
解:∵原式=(52)7-512
=514-512
=512×(52-1)
=24×512
=120×511
=30×4×511,
∴257-512能被30整除.
6.D
解析:,
∴另一个因式为D.
7.D
解析:==8n.
8.
解析:.
9.
解析:原式=.
10.6
解析:,
把代入得,
再把代入得.
11.解:(1)原式===.
(2)原式=(m-2)(n2-4)=(m-2)(n+2)(n-2).
12.解:原式=x(4x -y )=x(2x+y)(2x-y),
当x=10,y=10时,2x+y=30,2x-y=10,
所以密码为103010或101030或301010.
13.解:(1),
原式;
(2),
,
.
14.解:∵(a+b)2-(b+c)2=0,
∴(a+b+b+c) (a+b-b-c)=0,
(a+2b+c) (a-c)=0,
∵a+2b+c>0,
∴ a-c=0,即a=c.
所以这个三角形是等腰三角形.
15.解:正确.
A×B﹣C=(x﹣y+1)(x+y+1)﹣[(x+y)(x﹣y)+2x],
=(x+1﹣y)(x+1+y)﹣(x2﹣y2+2x),
=x2+2x+1﹣y2﹣x2+y2﹣2x,
=1;
∴x,y的取值与A×B﹣C的值无关.
1
1.因式分解:m2﹣4y2=( )
A.(m+2y)(m﹣2y) B.(2m+y)(2m﹣y)
C.(m+2y)(2m﹣y) D.(2m+y)(m﹣2y)
2.下列各式中不能用平方差公式分解的是( )
A. B. C. D.
3.若=8×10×12,则k=( )
A.12 B.10 C.8 D.6
4.下列各式中,能用平方差公式分解因式的是( )
A.x2+4y2 B.﹣x2+4y2 C.x2﹣2y+1 D.﹣x2﹣4y2
5.利用因式分解能说明:257-512能被( )整除.
A.5 B.10 C.22 D.30
6.有一个因式是,则另一个因式为( )
A. B. C. D.
7.当为正整数时,代数式一定是下面哪个数的倍数( )
A.3 B.5 C.7 D.8
8.因式分解:______.
9.把分解因式得_______.
10.若实数a,b满足,则代数式的值为_______________.
11.因式分解:
(1);(2)n2(m-2)+4(2-m).
12. 在日常生活中,如取款、上网需要密码,有一种因式分解法产生密码,例如,当 x=9,y=9 时, x-y=0 ,x+y=18, x2+y2=162,则密码 018162.对于多项式,取 x=10,y=10,用上述方法产生密码是什么?
13. 如图,是一道例题及部分解答过程,其中A,B是两个关于x,y的二项式.
请仔细观察上面的例题及解答过程,完成下列问题∶
(1)直接写出多项式A和 B,并求出该例题的运算结果;
(2)求多项式A与B的平方差.
14. 若a,b,c 是三角形的三边长,且满足(a+b)2- (b+c)2=0 ,判断三角形的形状.
15. 已知A=x-y+1,B=x+y+1,C=(x+y)(x-y)+2x.两位同学对x,y分别取了不同的值,求出A,B,C的值各不相同,但A×B-C的值却总是一样的.由此这两位同学得出结论:无论x,y取何值,A×B-C的值不变.你认为这个结论正确吗?请说明理由.
参考答案
1. A
解析:m2-4y2=(m+2y)(m-2y).
2.C
解析:A.=(2+x)(2﹣x),可以用平方差公式分解因式,故此选项错误;
B.=(y+x)(y﹣x),可以用平方差公式分解因式,故此选项错误;
C.,不可以用平方差公式分解因式,故此选项正确;
D.=(1+2x)(1﹣2x),可以用平方差公式分解因式,故此选项错误.
3.B
解析:8×10×12,∴k=10.
4.B
解析:A.两项的符号相同,不能用平方差公式分解因式;
B.是与的平方的差,能用平方差公式分解因式;
C.是三项不能用平方差公式分解因式;
D.两项的符号相同,不能用平方差公式分解因式.
5.D
解:∵原式=(52)7-512
=514-512
=512×(52-1)
=24×512
=120×511
=30×4×511,
∴257-512能被30整除.
6.D
解析:,
∴另一个因式为D.
7.D
解析:==8n.
8.
解析:.
9.
解析:原式=.
10.6
解析:,
把代入得,
再把代入得.
11.解:(1)原式===.
(2)原式=(m-2)(n2-4)=(m-2)(n+2)(n-2).
12.解:原式=x(4x -y )=x(2x+y)(2x-y),
当x=10,y=10时,2x+y=30,2x-y=10,
所以密码为103010或101030或301010.
13.解:(1),
原式;
(2),
,
.
14.解:∵(a+b)2-(b+c)2=0,
∴(a+b+b+c) (a+b-b-c)=0,
(a+2b+c) (a-c)=0,
∵a+2b+c>0,
∴ a-c=0,即a=c.
所以这个三角形是等腰三角形.
15.解:正确.
A×B﹣C=(x﹣y+1)(x+y+1)﹣[(x+y)(x﹣y)+2x],
=(x+1﹣y)(x+1+y)﹣(x2﹣y2+2x),
=x2+2x+1﹣y2﹣x2+y2﹣2x,
=1;
∴x,y的取值与A×B﹣C的值无关.
1
