初中数学人教版八下17.1.2勾股定理的应用教案
文档属性
| 名称 | 初中数学人教版八下17.1.2勾股定理的应用教案 |  | |
| 格式 | docx | ||
| 文件大小 | 207.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 13:01:18 | ||
图片预览


文档简介
17.1.2勾股定理的应用
教学内容分析
勾股定理是中学数学重要定理之一,它揭示了直角三角形三边之间的数量关系. 在利用勾股定理解决实际生活问题的过程中,能从实际问题中抽象出直角三角形这一几何模型,利用勾股定理建立已知边与未知边长度之间的联系,并进一步求出未知边长.强化转化思想,培养学生解决现实问题的意识和应用能力.
运用勾股定理证明直角三角形全等的HL判定定理,从中进一步确认,在直角三角形中,只要两边的大小确定,则这个三角形的形状大小就确定了.运用勾股定理,通过作直角三角形,画出了长度为无理数的线段,并学习在数轴上画出无理数表示的点的方法.通过本课的学习,体会勾股定理在数学中的地位和作用.教学时,应引导学生注意构造勾股定理的使用条件,在应用定理时关注数形结合和分类讨论的思想.
教学目标
1.能运用勾股定理及直角三角形的判定条件解决实际问题,感受数学的“转化”思想,体会数学的应用价值.
2.能用勾股定理证明直角三角形全等的“斜边、直角边”判定定理,能应用勾股定理在数轴上画出表示无理数的点.
教学重难点
【重点】勾股定理的实际应用问题.
【难点】用勾股定理作出长度为无理数的线段.
教学方法
启发法、探究法.
教学过程
(一)情境导入
数学来源于生活,勾股定理的应用在生活中无处不在.
如图,是一个边长为1的正方体硬纸盒,现在A处有一只蚂蚁,想沿着正方体的外表面到达B处吃食物,求蚂蚁爬行的最短距离是多少.
意图:让学生通过生活中的实际问题来引发思考,导入本节勾股定理的应用学习.
效果:学生知道了勾股定理的应用在生活中无处不在.
新课讲授
勾股定理的应用举例:
例1 一个门框的尺寸如图所示,一块长3m,宽2.2m的长方形薄木板能否从门框内通过?为什么?
问题1 木板进门框有几种方法?
问题2 你认为选择哪种方法比较好?你能说出你这种方法通过的最大长度是什么?
学生发现横着或竖着都进不去,应当想到试试斜着通过门框,把实际问题转化为一个直角三角形的问题,求出直角三角形的斜边长再作比较.
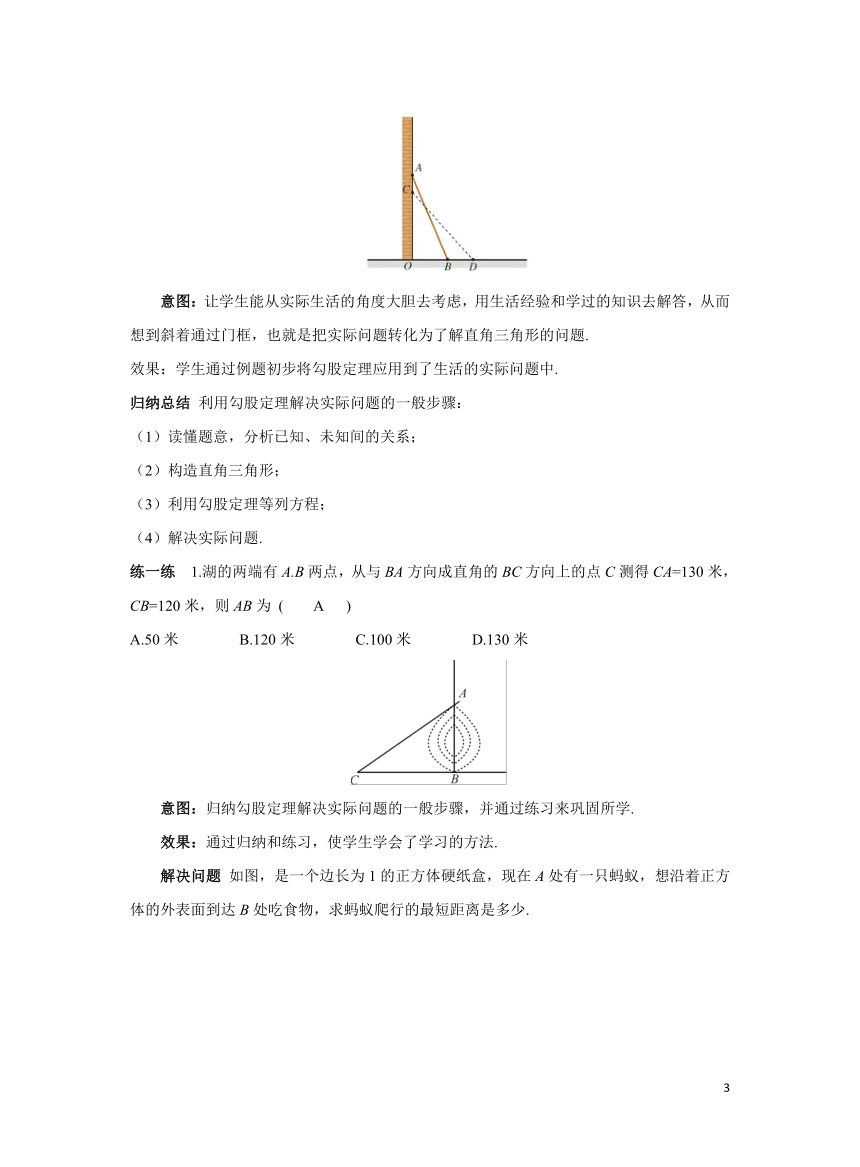
例2 如图所示,一架2.6m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4 m. 如果梯子的顶端A沿墙下滑0.5 m,那么梯子底端B也外移0.5 m吗?
问题1 下滑前梯子底端B离墙角O的距离是多少?
问题2 下滑前后梯子与墙面、地面构成的两个直角三角形,什么量没有发生变化?
问题3 下滑后梯子底端外移的距离是哪条线段的长度?如何计算?
意图:让学生能从实际生活的角度大胆去考虑,用生活经验和学过的知识去解答,从而想到斜着通过门框,也就是把实际问题转化为了解直角三角形的问题.
效果:学生通过例题初步将勾股定理应用到了生活的实际问题中.
归纳总结 利用勾股定理解决实际问题的一般步骤:
读懂题意,分析已知、未知间的关系;
构造直角三角形;
利用勾股定理等列方程;
解决实际问题.
练一练 1.湖的两端有A.B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为 ( A )
A.50米 B.120米 C.100米 D.130米
意图:归纳勾股定理解决实际问题的一般步骤,并通过练习来巩固所学.
效果:通过归纳和练习,使学生学会了学习的方法.
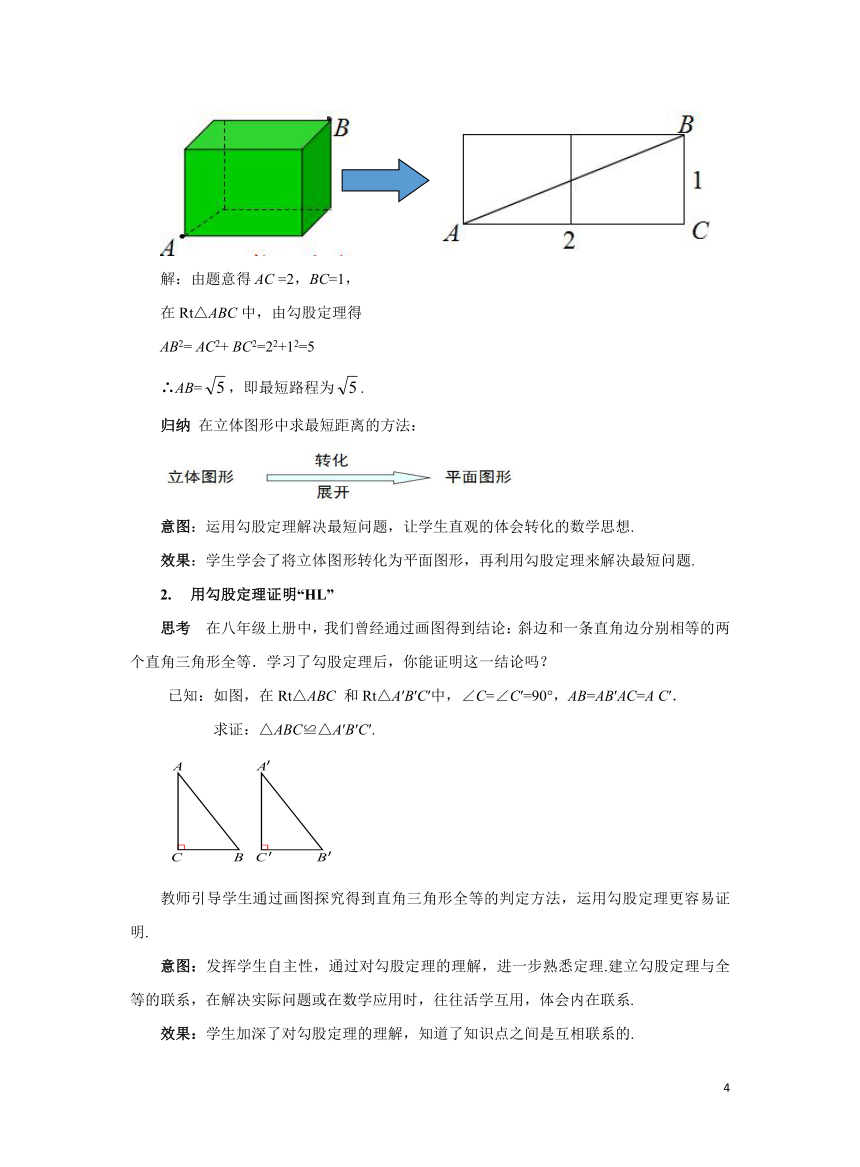
解决问题 如图,是一个边长为1的正方体硬纸盒,现在A处有一只蚂蚁,想沿着正方体的外表面到达B处吃食物,求蚂蚁爬行的最短距离是多少.
解:由题意得AC =2,BC=1,
在Rt△ABC中,由勾股定理得
AB2= AC2+ BC2=22+12=5
∴AB=,即最短路程为.
归纳 在立体图形中求最短距离的方法:
意图:运用勾股定理解决最短问题,让学生直观的体会转化的数学思想.
效果:学生学会了将立体图形转化为平面图形,再利用勾股定理来解决最短问题.
用勾股定理证明“HL”
思考 在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
已知:如图,在Rt△ABC 和Rt△A′B′C′中,∠C=∠C′=90°,AB=AB′AC=A C′.
求证:△ABC≌△A′B′C′.
教师引导学生通过画图探究得到直角三角形全等的判定方法,运用勾股定理更容易证明.
意图:发挥学生自主性,通过对勾股定理的理解,进一步熟悉定理.建立勾股定理与全等的联系,在解决实际问题或在数学应用时,往往活学互用,体会内在联系.
效果:学生加深了对勾股定理的理解,知道了知识点之间是互相联系的.
用勾股定理在数轴上表示无理数
探究 我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示的点吗?
问题1 我们知道数轴上的点与实数一一对应,有的表示有理数,有的表示无理数.你能在数轴上分别画出表示3,-2.5的点吗?
问题2 求下列三角形的各边长.
问题3 长为的线段能是直角边的长都为正整数的直角三角形的斜边吗?
思考 根据上面问题你能在数轴上画出表示的点吗?
步骤:
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示的点.
归纳总结 利用勾股定理表示无理数的方法:
利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.
以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
类比迁移 类似地,利用勾股定理可以作出长为...的线段.
教师指导学生寻找长为,,,...这样的包含在直角三角形中的线段.从而得到一个“数学海螺”.
意图:利用勾股定理和数轴上的点表示实数,将数和图形联系在一起,让学生领会了数形结合的思想,同时也加深了对勾股定理、数轴和实数的理解,规范学生的作图语言和作图方法.
效果:学生学会了如何在数轴上作图找到表示无理数的点.
例4 如图,数轴上点A所表示的数为a,求a的值.
易错点拨:求点表示的数时注意画弧的起点不从原点起,因而所表示的数不是斜边长.
意图:利用尺规作图和勾股定理画出数轴上的无理数点,进一步体会数轴上的点与实数一一对应的理论.
效果:学生加深了对数轴上无理数的作图的理解.
课堂练习
如图,有两棵树,一棵高8米,另一棵2米,两棵对相距8米.一只鸟从一棵树的树梢飞到另一棵的树梢,问小鸟至少飞行(B)
8米 B.10米 C.12米 D.14米
2.如图,在边长为1个单位长度的小正方形组成的网格中,点A.B都是格点,则线段AB的长度为(A )
A.5 B.6 C.7 D.25
3.如图,学校教学楼前有一块长方形长为4米,宽为3米的草坪,有极少数人为了避开拐角走“捷径”,在草坪内走出了一条“径路”,却踩伤了花草.
(1)求这条“径路”的长;
(2)他们仅仅少走了几步(假设2步为1米)?
解:(1)在Rt△ ABC中,
根据勾股定理得
∴这条“径路”的长为5米.
(2)他们仅仅少走了
(3+4-5)×2=4(步).
有一个圆柱形油罐,要以A点环绕油罐建梯子,正好建在A点的正上方点B处,问梯子最短需多少米(已知油罐的底面半径是2 m,高AB是5 m,π取3)?
解:油罐的展开图如图,则AB'为梯子的最短距离.
∵AA'=2×3×2=12, A'B'=5,
∴AB'=13. 即梯子最短需13米.
意图:应用勾股定理解决生活中的实际问题和几何中的最短问题.
效果:检测了学生对勾股定理应用的掌握情况.
课堂小结
先让学生自己总结反思,然后同学之间进行交流,再找学生谈谈自己的收获.
1.勾股定理的应用举例
方法:(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
2.利用勾股定理证明“HL”
3.利用勾股定理在数轴上表示无理数
方法:(1)利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
意图:总结反思是一节课必不可少的环节,有助于学生巩固所学知识和技能.
效果:学生对本节课所学知识有了系统的回顾.
作业布置
完成配套练习
板书设计
17.1.2勾股定理的应用
1.勾股定理的应用举例
方法:(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
2.利用勾股定理证明“HL”
3.利用勾股定理在数轴上表示无理数
方法:(1)利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
课后反思
本节课创设蚂蚁觅食的情境导入,抛出问题,激发学生学习本节课来解决问题的好奇心,让学生体会数学源于生活,数学服务于生活.授课过程中注重用一系列的问题来启发学生的思考,引导学生对知识运用的探究和方法的归纳总结,让学生学会学习.本节课将几何图形直观的展示给学生,有意培养学生几何直观的数学核心素养.
1
教学内容分析
勾股定理是中学数学重要定理之一,它揭示了直角三角形三边之间的数量关系. 在利用勾股定理解决实际生活问题的过程中,能从实际问题中抽象出直角三角形这一几何模型,利用勾股定理建立已知边与未知边长度之间的联系,并进一步求出未知边长.强化转化思想,培养学生解决现实问题的意识和应用能力.
运用勾股定理证明直角三角形全等的HL判定定理,从中进一步确认,在直角三角形中,只要两边的大小确定,则这个三角形的形状大小就确定了.运用勾股定理,通过作直角三角形,画出了长度为无理数的线段,并学习在数轴上画出无理数表示的点的方法.通过本课的学习,体会勾股定理在数学中的地位和作用.教学时,应引导学生注意构造勾股定理的使用条件,在应用定理时关注数形结合和分类讨论的思想.
教学目标
1.能运用勾股定理及直角三角形的判定条件解决实际问题,感受数学的“转化”思想,体会数学的应用价值.
2.能用勾股定理证明直角三角形全等的“斜边、直角边”判定定理,能应用勾股定理在数轴上画出表示无理数的点.
教学重难点
【重点】勾股定理的实际应用问题.
【难点】用勾股定理作出长度为无理数的线段.
教学方法
启发法、探究法.
教学过程
(一)情境导入
数学来源于生活,勾股定理的应用在生活中无处不在.
如图,是一个边长为1的正方体硬纸盒,现在A处有一只蚂蚁,想沿着正方体的外表面到达B处吃食物,求蚂蚁爬行的最短距离是多少.
意图:让学生通过生活中的实际问题来引发思考,导入本节勾股定理的应用学习.
效果:学生知道了勾股定理的应用在生活中无处不在.
新课讲授
勾股定理的应用举例:
例1 一个门框的尺寸如图所示,一块长3m,宽2.2m的长方形薄木板能否从门框内通过?为什么?
问题1 木板进门框有几种方法?
问题2 你认为选择哪种方法比较好?你能说出你这种方法通过的最大长度是什么?
学生发现横着或竖着都进不去,应当想到试试斜着通过门框,把实际问题转化为一个直角三角形的问题,求出直角三角形的斜边长再作比较.
例2 如图所示,一架2.6m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4 m. 如果梯子的顶端A沿墙下滑0.5 m,那么梯子底端B也外移0.5 m吗?
问题1 下滑前梯子底端B离墙角O的距离是多少?
问题2 下滑前后梯子与墙面、地面构成的两个直角三角形,什么量没有发生变化?
问题3 下滑后梯子底端外移的距离是哪条线段的长度?如何计算?
意图:让学生能从实际生活的角度大胆去考虑,用生活经验和学过的知识去解答,从而想到斜着通过门框,也就是把实际问题转化为了解直角三角形的问题.
效果:学生通过例题初步将勾股定理应用到了生活的实际问题中.
归纳总结 利用勾股定理解决实际问题的一般步骤:
读懂题意,分析已知、未知间的关系;
构造直角三角形;
利用勾股定理等列方程;
解决实际问题.
练一练 1.湖的两端有A.B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为 ( A )
A.50米 B.120米 C.100米 D.130米
意图:归纳勾股定理解决实际问题的一般步骤,并通过练习来巩固所学.
效果:通过归纳和练习,使学生学会了学习的方法.
解决问题 如图,是一个边长为1的正方体硬纸盒,现在A处有一只蚂蚁,想沿着正方体的外表面到达B处吃食物,求蚂蚁爬行的最短距离是多少.
解:由题意得AC =2,BC=1,
在Rt△ABC中,由勾股定理得
AB2= AC2+ BC2=22+12=5
∴AB=,即最短路程为.
归纳 在立体图形中求最短距离的方法:
意图:运用勾股定理解决最短问题,让学生直观的体会转化的数学思想.
效果:学生学会了将立体图形转化为平面图形,再利用勾股定理来解决最短问题.
用勾股定理证明“HL”
思考 在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
已知:如图,在Rt△ABC 和Rt△A′B′C′中,∠C=∠C′=90°,AB=AB′AC=A C′.
求证:△ABC≌△A′B′C′.
教师引导学生通过画图探究得到直角三角形全等的判定方法,运用勾股定理更容易证明.
意图:发挥学生自主性,通过对勾股定理的理解,进一步熟悉定理.建立勾股定理与全等的联系,在解决实际问题或在数学应用时,往往活学互用,体会内在联系.
效果:学生加深了对勾股定理的理解,知道了知识点之间是互相联系的.
用勾股定理在数轴上表示无理数
探究 我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示的点吗?
问题1 我们知道数轴上的点与实数一一对应,有的表示有理数,有的表示无理数.你能在数轴上分别画出表示3,-2.5的点吗?
问题2 求下列三角形的各边长.
问题3 长为的线段能是直角边的长都为正整数的直角三角形的斜边吗?
思考 根据上面问题你能在数轴上画出表示的点吗?
步骤:
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示的点.
归纳总结 利用勾股定理表示无理数的方法:
利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.
以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
类比迁移 类似地,利用勾股定理可以作出长为...的线段.
教师指导学生寻找长为,,,...这样的包含在直角三角形中的线段.从而得到一个“数学海螺”.
意图:利用勾股定理和数轴上的点表示实数,将数和图形联系在一起,让学生领会了数形结合的思想,同时也加深了对勾股定理、数轴和实数的理解,规范学生的作图语言和作图方法.
效果:学生学会了如何在数轴上作图找到表示无理数的点.
例4 如图,数轴上点A所表示的数为a,求a的值.
易错点拨:求点表示的数时注意画弧的起点不从原点起,因而所表示的数不是斜边长.
意图:利用尺规作图和勾股定理画出数轴上的无理数点,进一步体会数轴上的点与实数一一对应的理论.
效果:学生加深了对数轴上无理数的作图的理解.
课堂练习
如图,有两棵树,一棵高8米,另一棵2米,两棵对相距8米.一只鸟从一棵树的树梢飞到另一棵的树梢,问小鸟至少飞行(B)
8米 B.10米 C.12米 D.14米
2.如图,在边长为1个单位长度的小正方形组成的网格中,点A.B都是格点,则线段AB的长度为(A )
A.5 B.6 C.7 D.25
3.如图,学校教学楼前有一块长方形长为4米,宽为3米的草坪,有极少数人为了避开拐角走“捷径”,在草坪内走出了一条“径路”,却踩伤了花草.
(1)求这条“径路”的长;
(2)他们仅仅少走了几步(假设2步为1米)?
解:(1)在Rt△ ABC中,
根据勾股定理得
∴这条“径路”的长为5米.
(2)他们仅仅少走了
(3+4-5)×2=4(步).
有一个圆柱形油罐,要以A点环绕油罐建梯子,正好建在A点的正上方点B处,问梯子最短需多少米(已知油罐的底面半径是2 m,高AB是5 m,π取3)?
解:油罐的展开图如图,则AB'为梯子的最短距离.
∵AA'=2×3×2=12, A'B'=5,
∴AB'=13. 即梯子最短需13米.
意图:应用勾股定理解决生活中的实际问题和几何中的最短问题.
效果:检测了学生对勾股定理应用的掌握情况.
课堂小结
先让学生自己总结反思,然后同学之间进行交流,再找学生谈谈自己的收获.
1.勾股定理的应用举例
方法:(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
2.利用勾股定理证明“HL”
3.利用勾股定理在数轴上表示无理数
方法:(1)利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
意图:总结反思是一节课必不可少的环节,有助于学生巩固所学知识和技能.
效果:学生对本节课所学知识有了系统的回顾.
作业布置
完成配套练习
板书设计
17.1.2勾股定理的应用
1.勾股定理的应用举例
方法:(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
2.利用勾股定理证明“HL”
3.利用勾股定理在数轴上表示无理数
方法:(1)利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
课后反思
本节课创设蚂蚁觅食的情境导入,抛出问题,激发学生学习本节课来解决问题的好奇心,让学生体会数学源于生活,数学服务于生活.授课过程中注重用一系列的问题来启发学生的思考,引导学生对知识运用的探究和方法的归纳总结,让学生学会学习.本节课将几何图形直观的展示给学生,有意培养学生几何直观的数学核心素养.
1
