初中数学人教版八下18.2.3正方形 教案
文档属性
| 名称 | 初中数学人教版八下18.2.3正方形 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 809.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 13:11:51 | ||
图片预览

文档简介
18.2.3正方形
教学内容分析
正方形是最特殊的平行四边形,因此正方形具有菱形,矩形,平行四边形的所有性质,当然正方形的判定条件也最多,既是菱形,又是矩形,才能是正方形. 因此正方形的研究思路借鉴了其他特殊平行四边形的研究方法,从动态的角度演示几何图形的变化,这是一个从一般到特殊的动态演变过程,培养学生几何直观的数学素养,同时将学过的几种平行四边形进行对比,辨析各种图形的区别和联系.
二、教学目标
1.理解正方形的概念.
2.探索并证明正方形的性质和判定定理,并了解平行四边形、矩形、菱形之间的联系和区别.
3.会应用正方形的性质和判定定理解决相关证明及计算问题.
三、教学重难点
【重点】探索并证明正方形的性质和判定定理,并了解平行四边形、矩形、菱形之间的联系和区别.
【难点】会应用正方形的性质和判定定理解决相关证明及计算问题.
四、教学方法
问题启发法、观察归纳法、探究法.
五、教学过程
(一)图片导入
观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.
意图:从身边熟悉的图形出发,并从中抽象出正方形,使学生感受到数学学习是有趣、有用的,从而引入课题.
效果:激发了学生学习正方形的兴趣.
正方形的定义
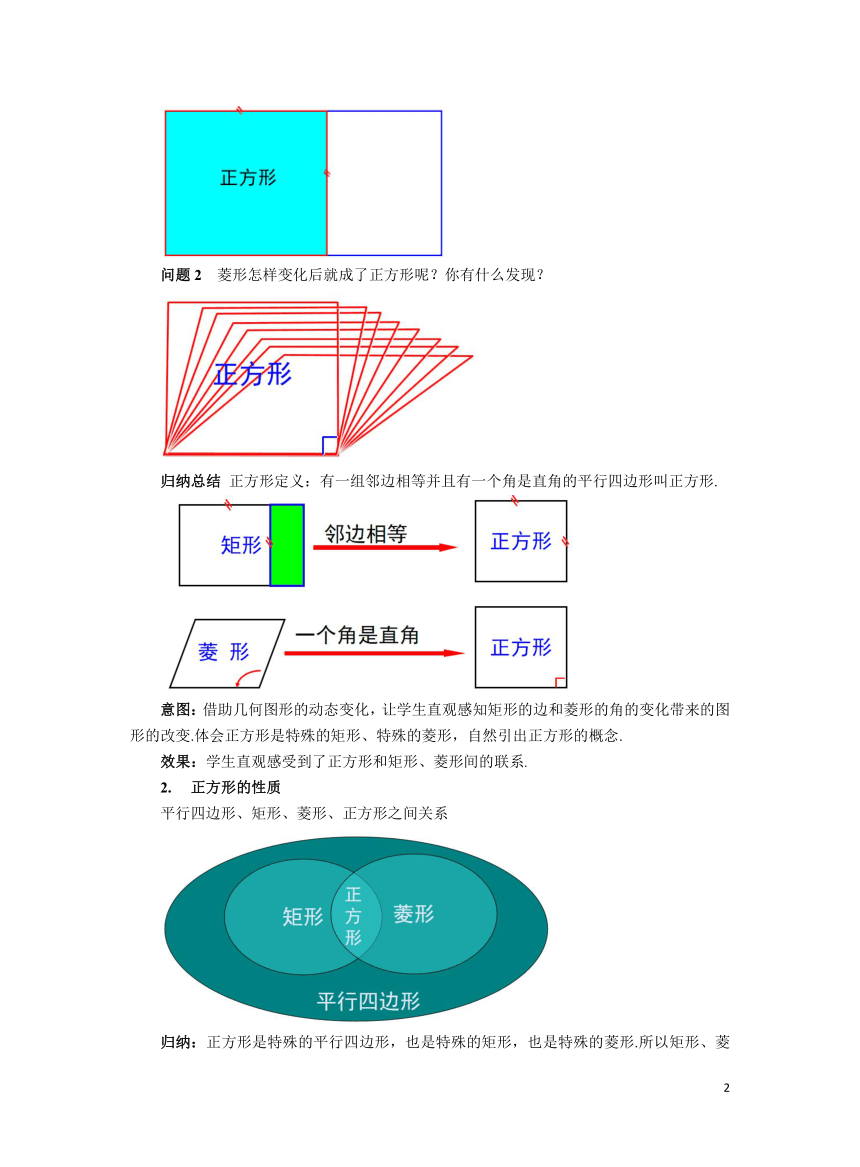
问题1 矩形怎样变化后就成了正方形呢?你有什么发现?
问题2 菱形怎样变化后就成了正方形呢?你有什么发现?
归纳总结 正方形定义:有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
意图:借助几何图形的动态变化,让学生直观感知矩形的边和菱形的角的变化带来的图形的改变.体会正方形是特殊的矩形、特殊的菱形,自然引出正方形的概念.
效果:学生直观感受到了正方形和矩形、菱形间的联系.
正方形的性质
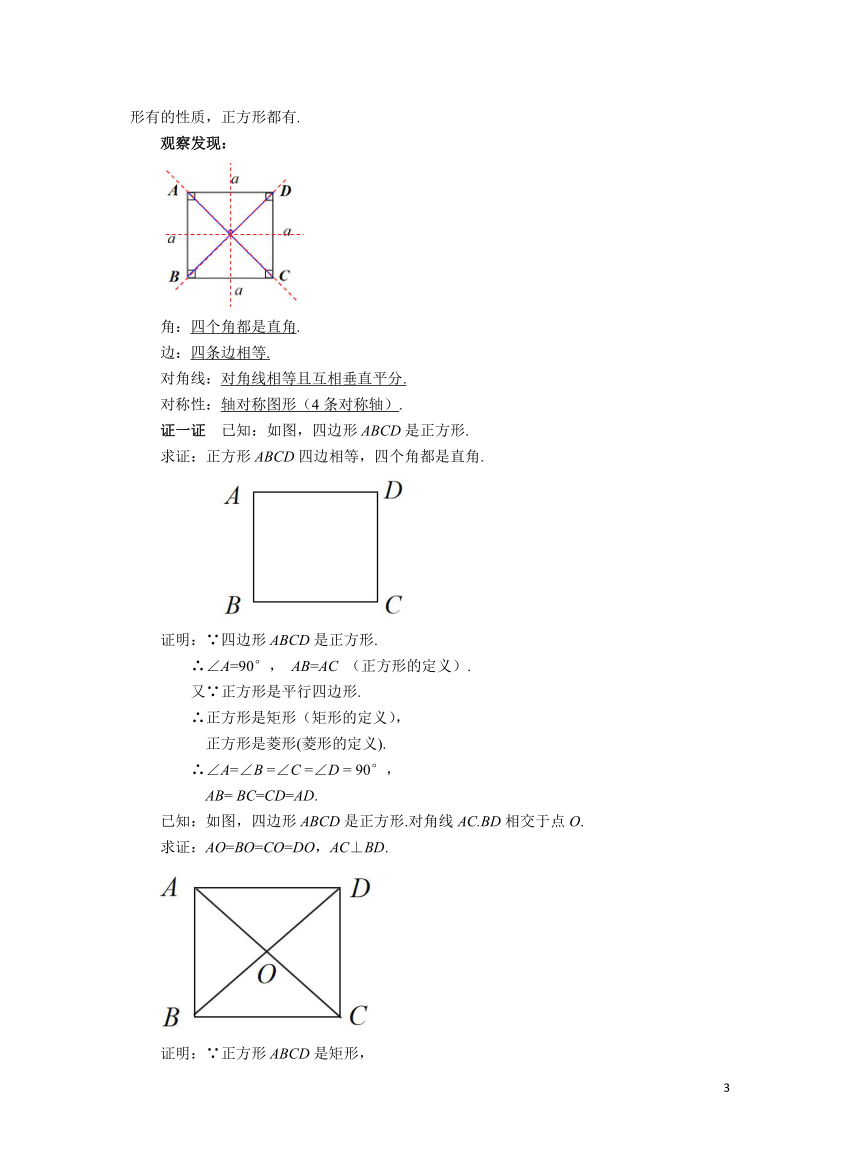
平行四边形、矩形、菱形、正方形之间关系
归纳:正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
观察发现:
角:四个角都是直角.
边:四条边相等.
对角线:对角线相等且互相垂直平分.
对称性:轴对称图形(4条对称轴).
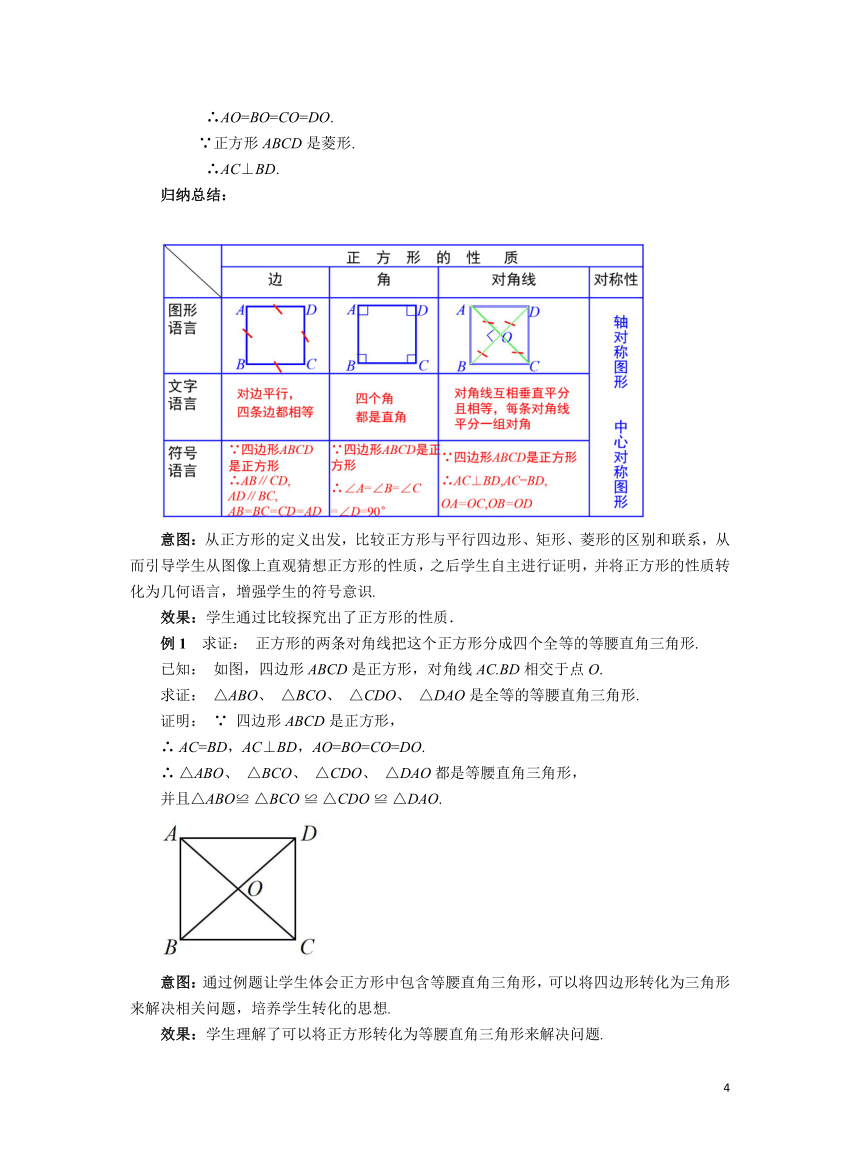
证一证 已知:如图,四边形ABCD是正方形.
求证:正方形ABCD四边相等,四个角都是直角.
证明:∵四边形ABCD是正方形.
∴∠A=90°, AB=AC (正方形的定义).
又∵正方形是平行四边形.
∴正方形是矩形(矩形的定义),
正方形是菱形(菱形的定义).
∴∠A=∠B =∠C =∠D = 90°,
AB= BC=CD=AD.
已知:如图,四边形ABCD是正方形.对角线AC.BD相交于点O.
求证:AO=BO=CO=DO,AC⊥BD.
证明:∵正方形ABCD是矩形,
∴AO=BO=CO=DO.
∵正方形ABCD是菱形.
∴AC⊥BD.
归纳总结:
意图:从正方形的定义出发,比较正方形与平行四边形、矩形、菱形的区别和联系,从而引导学生从图像上直观猜想正方形的性质,之后学生自主进行证明,并将正方形的性质转化为几何语言,增强学生的符号意识.
效果:学生通过比较探究出了正方形的性质.
例1 求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
已知: 如图,四边形ABCD是正方形,对角线AC.BD相交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,
并且△ABO≌ △BCO ≌ △CDO ≌ △DAO.
意图:通过例题让学生体会正方形中包含等腰直角三角形,可以将四边形转化为三角形来解决相关问题,培养学生转化的思想.
效果:学生理解了可以将正方形转化为等腰直角三角形来解决问题.
练一练 (1)正方形具有而矩形不一定具有的性质是 ( B )
A.四个角相等
B.对角线互相垂直平分
C.对角互补
D.对角线相等
(2)正方形具有而菱形不一定具有的性质( D )
A.四条边相等
B.对角线互相垂直平分
C.对角线平分一组对角
D.对角线相等
3.正方形的判定
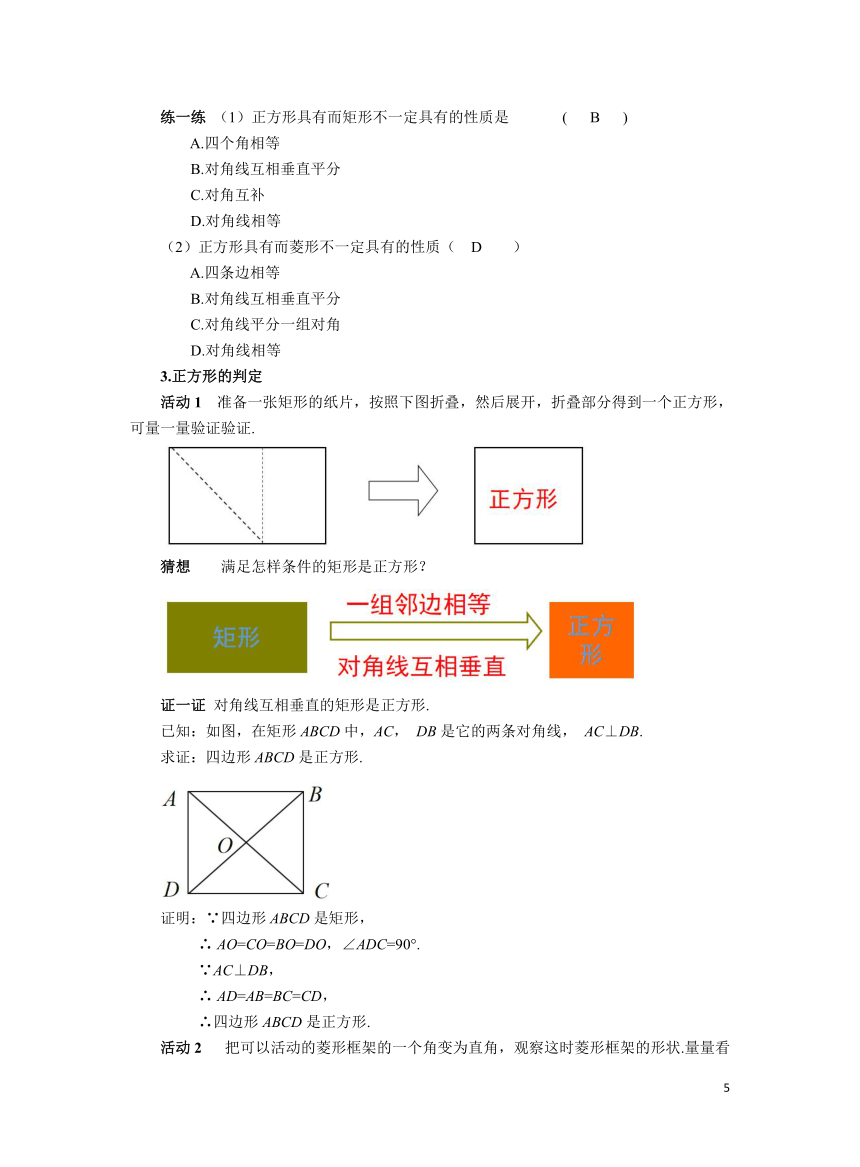
活动1 准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形,可量一量验证验证.
猜想 满足怎样条件的矩形是正方形?
证一证 对角线互相垂直的矩形是正方形.
已知:如图,在矩形ABCD中,AC, DB是它的两条对角线, AC⊥DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴ AO=CO=BO=DO,∠ADC=90°.
∵AC⊥DB,
∴ AD=AB=BC=CD,
∴四边形ABCD是正方形.
活动2 把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状.量量看是不是正方形.
猜想 满足怎样条件的菱形是正方形?
证一证 对角线相等的菱形是正方形.
已知:如图,在菱形ABCD中,AC.DB是它的两条对角线, AC=DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥DB.
∵AC=DB,
∴ AO=BO=CO=DO,
∴△AOD,△AOB,△COD,△BOC是等腰直角三角形,
∴∠DAB=∠ABC=∠BCD=∠ADC=90°,
∴四边形ABCD是正方形.
总结归纳 正方形判定的几条途径:
意图:通过学生熟悉的折纸引入正方形的判定,经历图形变化演绎的过程,初步得出正方形的判定,然后学生自己证明正方形的判定定理,归纳出判定正方形的几条途径,也更清楚的理解了正方形和其他特殊平行四边形的关系.
效果:学生通过观察探究得出正方形判定的几种方法,更清楚的理解了正方形和平行四边形、矩形、菱形间的关系.
练一练
在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是( C )
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
例2 在正方形ABCD中,点E.F、M、N分别在各边上,且AE=BF=CM=DN.四边形EFMN是正方形吗?为什么?
证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.
∵AE=BF=CM=DN,
∴AN=BE=CF=DM.
做一做:顺次连接任意四边形各边中点所得的四边形是平行四边形.顺次连接矩形、正方形各边中点能得到怎样的特殊平行四边形?
意图:学生结合中位线的知识来判断中点四边形的形状,巩固平行四边形、菱形、正方形等平行四边形的判定,培养学生将所学知识进行整合联系解决问题的能力.
效果:学生巩固了平行四边形、菱形、正方形的判定方法.
课堂练习
1.平行四边形、矩形、菱形、正方形都具有的是(A )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等
2.一个正方形的对角线长为2cm,则它的面积是 ( A )
A.2cm2 B.4cm2 C.6cm2 D.8cm2
如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( D )
A.当AB=BC时,四边形ABCD是菱形
B.当AC⊥BD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD时,四边形ABCD是正方形
4.如图,已知正方形ABCD ,以AB为边向正方形外作等边△ABE,连结DE 、 CE ,求∠DEC的度数.
解:∵△ABE是等边三角形.
∴AB =AE=BE,
∠ABE=∠BEA=∠EAB =60°.
又∵四边形ABCD是正方形.
∴AD=BC=AE=BE,∠DAB=∠ABC=90°.
∴∠DAE=∠CBE=150°.
∴∠AED=∠EDA=∠CEB=∠BCE=15°.
∴∠DEC=∠AEB-∠AED-∠CEB=30°.
5.如图,△ABC中,D是BC上任意一点,DE∥AC,DF∥AB.
(1)试说明四边形AEDF的形状,并说明理由.
(2)连接AD,当AD满足什么条件时,四边形AEDF为菱形,为什么?
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AEDF为正方形,不说明理由.
解:(1)∵DE∥AC,DF∥AB,
∴四边形AEDF为平行四边形.
(2)∵四边形AEDF为菱形,
∴AD平分∠BAC,
则AD平分∠BAC时,四边形AEDF为菱形.
(3)由四边形AEDF为正方形
∴∠BAC=90°,
∴△ABC是以BC为斜边的直角三角形即可.
意图:让学生初步使用学到的知识解决问题,并体会学习的乐趣.
效果:检测了学生对正方形性质和判定的理解和运用.
课堂小结
引导学生回顾本节课所学内容,谈谈自己的收获.
1. 正方形的定义:有一组邻边相等,并且有一个角是直角的平行四边形.
2. 正方形的性质:①四个角都是直角;
②四条边都相等;
③对角线相等且互相垂直平分.
3. 正方形的判定:对角线互相垂直的矩形是正方形.
对角线相等的菱形是正方形.
作业布置
完成配套练习
板书设计
18.2.3正方形
1. 正方形的定义:有一组邻边相等,并且有一个角是直角的平行四边形.
2. 正方形的性质:① 四个角都是直角;
② 四条边都相等;
③ 对角线相等且互相垂直平分.
3. 正方形的判定:对角线互相垂直的矩形是正方形.
对角线相等的菱形是正方形.
七、教学反思
正方形是学生都比较熟悉的图形,在本节课中没有设置过多的讨论环节,而是让学生从直观的图形演绎角度,让学生自己去比较辨析,去观察并证明正方形的性质,得出正方形是特殊的平行四边形,它集平行四边形、矩形、菱形的性质于一身.之后让学生利用图形直观观察正方形是怎样得到的,从而归纳正方形判定的几种方法.在整节课中注意将学生本章所学的知识点串联起来,重点培养学生的几何直观的核心素养.
1
教学内容分析
正方形是最特殊的平行四边形,因此正方形具有菱形,矩形,平行四边形的所有性质,当然正方形的判定条件也最多,既是菱形,又是矩形,才能是正方形. 因此正方形的研究思路借鉴了其他特殊平行四边形的研究方法,从动态的角度演示几何图形的变化,这是一个从一般到特殊的动态演变过程,培养学生几何直观的数学素养,同时将学过的几种平行四边形进行对比,辨析各种图形的区别和联系.
二、教学目标
1.理解正方形的概念.
2.探索并证明正方形的性质和判定定理,并了解平行四边形、矩形、菱形之间的联系和区别.
3.会应用正方形的性质和判定定理解决相关证明及计算问题.
三、教学重难点
【重点】探索并证明正方形的性质和判定定理,并了解平行四边形、矩形、菱形之间的联系和区别.
【难点】会应用正方形的性质和判定定理解决相关证明及计算问题.
四、教学方法
问题启发法、观察归纳法、探究法.
五、教学过程
(一)图片导入
观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.
意图:从身边熟悉的图形出发,并从中抽象出正方形,使学生感受到数学学习是有趣、有用的,从而引入课题.
效果:激发了学生学习正方形的兴趣.
正方形的定义
问题1 矩形怎样变化后就成了正方形呢?你有什么发现?
问题2 菱形怎样变化后就成了正方形呢?你有什么发现?
归纳总结 正方形定义:有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
意图:借助几何图形的动态变化,让学生直观感知矩形的边和菱形的角的变化带来的图形的改变.体会正方形是特殊的矩形、特殊的菱形,自然引出正方形的概念.
效果:学生直观感受到了正方形和矩形、菱形间的联系.
正方形的性质
平行四边形、矩形、菱形、正方形之间关系
归纳:正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
观察发现:
角:四个角都是直角.
边:四条边相等.
对角线:对角线相等且互相垂直平分.
对称性:轴对称图形(4条对称轴).
证一证 已知:如图,四边形ABCD是正方形.
求证:正方形ABCD四边相等,四个角都是直角.
证明:∵四边形ABCD是正方形.
∴∠A=90°, AB=AC (正方形的定义).
又∵正方形是平行四边形.
∴正方形是矩形(矩形的定义),
正方形是菱形(菱形的定义).
∴∠A=∠B =∠C =∠D = 90°,
AB= BC=CD=AD.
已知:如图,四边形ABCD是正方形.对角线AC.BD相交于点O.
求证:AO=BO=CO=DO,AC⊥BD.
证明:∵正方形ABCD是矩形,
∴AO=BO=CO=DO.
∵正方形ABCD是菱形.
∴AC⊥BD.
归纳总结:
意图:从正方形的定义出发,比较正方形与平行四边形、矩形、菱形的区别和联系,从而引导学生从图像上直观猜想正方形的性质,之后学生自主进行证明,并将正方形的性质转化为几何语言,增强学生的符号意识.
效果:学生通过比较探究出了正方形的性质.
例1 求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
已知: 如图,四边形ABCD是正方形,对角线AC.BD相交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,
并且△ABO≌ △BCO ≌ △CDO ≌ △DAO.
意图:通过例题让学生体会正方形中包含等腰直角三角形,可以将四边形转化为三角形来解决相关问题,培养学生转化的思想.
效果:学生理解了可以将正方形转化为等腰直角三角形来解决问题.
练一练 (1)正方形具有而矩形不一定具有的性质是 ( B )
A.四个角相等
B.对角线互相垂直平分
C.对角互补
D.对角线相等
(2)正方形具有而菱形不一定具有的性质( D )
A.四条边相等
B.对角线互相垂直平分
C.对角线平分一组对角
D.对角线相等
3.正方形的判定
活动1 准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形,可量一量验证验证.
猜想 满足怎样条件的矩形是正方形?
证一证 对角线互相垂直的矩形是正方形.
已知:如图,在矩形ABCD中,AC, DB是它的两条对角线, AC⊥DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴ AO=CO=BO=DO,∠ADC=90°.
∵AC⊥DB,
∴ AD=AB=BC=CD,
∴四边形ABCD是正方形.
活动2 把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状.量量看是不是正方形.
猜想 满足怎样条件的菱形是正方形?
证一证 对角线相等的菱形是正方形.
已知:如图,在菱形ABCD中,AC.DB是它的两条对角线, AC=DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥DB.
∵AC=DB,
∴ AO=BO=CO=DO,
∴△AOD,△AOB,△COD,△BOC是等腰直角三角形,
∴∠DAB=∠ABC=∠BCD=∠ADC=90°,
∴四边形ABCD是正方形.
总结归纳 正方形判定的几条途径:
意图:通过学生熟悉的折纸引入正方形的判定,经历图形变化演绎的过程,初步得出正方形的判定,然后学生自己证明正方形的判定定理,归纳出判定正方形的几条途径,也更清楚的理解了正方形和其他特殊平行四边形的关系.
效果:学生通过观察探究得出正方形判定的几种方法,更清楚的理解了正方形和平行四边形、矩形、菱形间的关系.
练一练
在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是( C )
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
例2 在正方形ABCD中,点E.F、M、N分别在各边上,且AE=BF=CM=DN.四边形EFMN是正方形吗?为什么?
证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.
∵AE=BF=CM=DN,
∴AN=BE=CF=DM.
做一做:顺次连接任意四边形各边中点所得的四边形是平行四边形.顺次连接矩形、正方形各边中点能得到怎样的特殊平行四边形?
意图:学生结合中位线的知识来判断中点四边形的形状,巩固平行四边形、菱形、正方形等平行四边形的判定,培养学生将所学知识进行整合联系解决问题的能力.
效果:学生巩固了平行四边形、菱形、正方形的判定方法.
课堂练习
1.平行四边形、矩形、菱形、正方形都具有的是(A )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等
2.一个正方形的对角线长为2cm,则它的面积是 ( A )
A.2cm2 B.4cm2 C.6cm2 D.8cm2
如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( D )
A.当AB=BC时,四边形ABCD是菱形
B.当AC⊥BD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD时,四边形ABCD是正方形
4.如图,已知正方形ABCD ,以AB为边向正方形外作等边△ABE,连结DE 、 CE ,求∠DEC的度数.
解:∵△ABE是等边三角形.
∴AB =AE=BE,
∠ABE=∠BEA=∠EAB =60°.
又∵四边形ABCD是正方形.
∴AD=BC=AE=BE,∠DAB=∠ABC=90°.
∴∠DAE=∠CBE=150°.
∴∠AED=∠EDA=∠CEB=∠BCE=15°.
∴∠DEC=∠AEB-∠AED-∠CEB=30°.
5.如图,△ABC中,D是BC上任意一点,DE∥AC,DF∥AB.
(1)试说明四边形AEDF的形状,并说明理由.
(2)连接AD,当AD满足什么条件时,四边形AEDF为菱形,为什么?
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AEDF为正方形,不说明理由.
解:(1)∵DE∥AC,DF∥AB,
∴四边形AEDF为平行四边形.
(2)∵四边形AEDF为菱形,
∴AD平分∠BAC,
则AD平分∠BAC时,四边形AEDF为菱形.
(3)由四边形AEDF为正方形
∴∠BAC=90°,
∴△ABC是以BC为斜边的直角三角形即可.
意图:让学生初步使用学到的知识解决问题,并体会学习的乐趣.
效果:检测了学生对正方形性质和判定的理解和运用.
课堂小结
引导学生回顾本节课所学内容,谈谈自己的收获.
1. 正方形的定义:有一组邻边相等,并且有一个角是直角的平行四边形.
2. 正方形的性质:①四个角都是直角;
②四条边都相等;
③对角线相等且互相垂直平分.
3. 正方形的判定:对角线互相垂直的矩形是正方形.
对角线相等的菱形是正方形.
作业布置
完成配套练习
板书设计
18.2.3正方形
1. 正方形的定义:有一组邻边相等,并且有一个角是直角的平行四边形.
2. 正方形的性质:① 四个角都是直角;
② 四条边都相等;
③ 对角线相等且互相垂直平分.
3. 正方形的判定:对角线互相垂直的矩形是正方形.
对角线相等的菱形是正方形.
七、教学反思
正方形是学生都比较熟悉的图形,在本节课中没有设置过多的讨论环节,而是让学生从直观的图形演绎角度,让学生自己去比较辨析,去观察并证明正方形的性质,得出正方形是特殊的平行四边形,它集平行四边形、矩形、菱形的性质于一身.之后让学生利用图形直观观察正方形是怎样得到的,从而归纳正方形判定的几种方法.在整节课中注意将学生本章所学的知识点串联起来,重点培养学生的几何直观的核心素养.
1
