初中数学华师大版七上4.6.3余角和补角 习题(含解析)
文档属性
| 名称 | 初中数学华师大版七上4.6.3余角和补角 习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 94.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 13:27:54 | ||
图片预览


文档简介
4.6.3 余角和补角 同步检测
选择题:
1.已知∠α=25°30',则它的补角为( )
A.25°30′ B.64° 30' C.164° 30' D.154°30′
2.一个角的余角是它的2倍,这个角的度数是()
A.30° B.45° C.60° D.75°
3.关于补角有下列四个叙述:①锐角的补角是钝角;②只有锐角才有补角;③互为补角的两个角不可能相等;④同角或等角的补角一定相等.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
4.如图,点O在直线AB上,∠COB=∠EOD=90°,下列说法错误的是( )
A.∠1=∠2相等 B.∠AOE与∠2互余
C.∠AOD与∠1互补 D.∠AOD与∠COD互补
5.下列说法正确的是()
A.一个角的补角一定大于它本身
B.一个角的余角一定小于它本身
C.一个钝角减去一个锐角的差一定是一个锐角
D.一个角的余角一定小于它的补角
6.若一个锐角和它的余角相等,则它的补角为( )
A.75° B.120° C.135° D.150°
7.有下列说法:
①若∠A+∠B+∠C=180°,则∠A,∠B,∠C互补;
②若∠1是∠2的余角,则∠2是∠1的余角;
③一个锐角的补角一定比它的余角大90°;
④互补的两个角中,一定是一个钝角与一个锐角.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8.互为补角的两个角的比是3:2,则较小角的余角等于( )
A.18° B.54° C.108° D.144°
填空题:
9.已知∠A=29°45',则∠A的余角的度数是 .
10.已知∠α=76°,∠β=41°31',求:
(1)∠β的余角的大小是 ;
(2)∠α的2倍与∠β的补角的差是 .
11.如图,AOB是直线,∠AOC=∠DOE=90°,则图中与∠BOD互余的角是
或 ,与∠DOE互补的角是 或 .
解答题:
12.已知一个角的余角比这个角补角的小12°,求这个角和它的余角的度数.
13.如图,已知∠BAC=90°,∠ADC=∠ADB=90°.①则图中有几对互余的角?②除直角以外,图中还有几对相等的角?说明理由.
14.①∠α的余角是 ,∠β的补角是 .
②已知∠α是∠β的2倍,∠α的余角的3倍等于∠β的补角,求∠α和∠β的度数.
15.如图,O是直线AB上的一点,∠BOD=∠COE=90°.
(1)写出图中与∠1互余的角;
(2)写出图中相等的角(直角除外);
(3)写出图中∠3的补角;
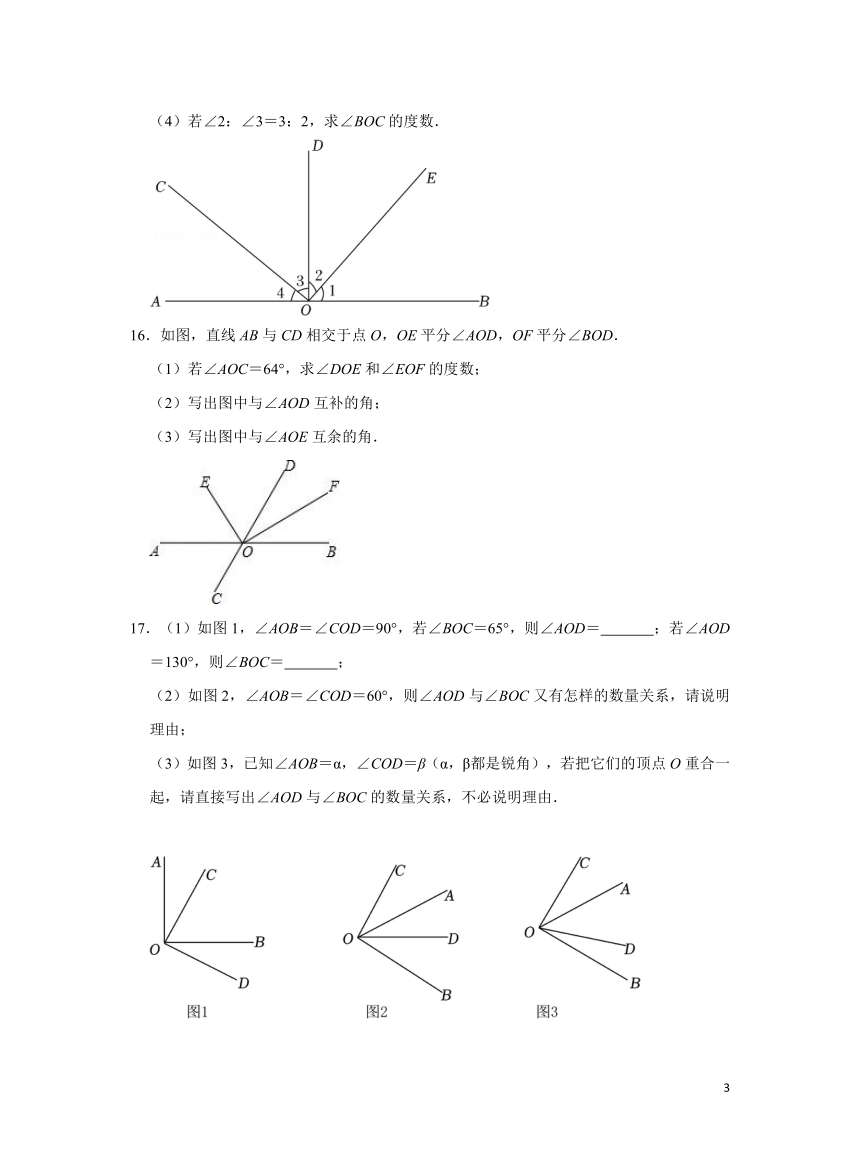
(4)若∠2:∠3=3:2,求∠BOC的度数.
16.如图,直线AB与CD相交于点O,OE平分∠AOD,OF平分∠BOD.
(1)若∠AOC=64°,求∠DOE和∠EOF的度数;
(2)写出图中与∠AOD互补的角;
(3)写出图中与∠AOE互余的角.
17.(1)如图1,∠AOB=∠COD=90°,若∠BOC=65°,则∠AOD= ;若∠AOD=130°,则∠BOC= ;
(2)如图2,∠AOB=∠COD=60°,则∠AOD与∠BOC又有怎样的数量关系,请说明理由;
(3)如图3,已知∠AOB=α,∠COD=β(α,β都是锐角),若把它们的顶点O重合一起,请直接写出∠AOD与∠BOC的数量关系,不必说明理由.
参考答案:
1.D解:180°﹣25°30′=154°30′.故选:D.
2.A解:设这个角为x度,根据 题意得:x+2x=90,解得:x=30,故这个角为30°.
3.B解:①若∠A是锐角,则180°﹣∠A>90°,即锐角的补角是钝角,那么①正确.
②任意角均有补角,那么②错误.
③直角的补角是直角,得互补的两个角也可能相等,那么③错误.
④同角或等角的补角相等,那么④正确.综上:正确的有①④,共2个.故选:B.
4.解:∵∠COB=∠EOD=90°,
∴∠1+∠COD=∠2+∠COD=90°,
∴∠1=∠2,故A选项正确;
∵∠AOE+∠1=90°,
∴∠AOE+∠2=90°,即∠AOE与∠2互余,故B选项正确;
∵∠COB=90°,
∵∠AOD+∠2=180°,
∵∠1=∠2,
∴∠AOD+∠1=180°,即∠AOD与∠1互补,故C选项正确;
无法判断∠AOD与∠COD是否互余,D选项错误;
故选:D.
5.D解:A不正确,钝角的补角是锐角小于它本身;B不正确,大于45°的角的余角就小于它本身,C不正确,例如130°减去10°的角差是120°还是钝角故正确答案是D.
6.C解:设这个角为α,它的余角也是α,则2α=90°解得:α=45°,180°-45°=135°故选C
7.B解:①补角一定指的是两个角之间的关系,错误.
②若∠1是∠2的补角,则∠2是∠1的补角,正确.
③同一个锐角的补角一定比它的余角大90°,正确,180﹣α﹣(90﹣α)=90.
④互补的两个角中,一定是一个钝角与一个锐角,错误,90°+90°=180°.
故选:B.
8.解:∵互为补角的两个角的比是3:2,
∴较大的角=180°×=108°,较小的角=180°×=72°,
∴较小角的余角=90°﹣72°=18°,
故选:A.
填空题
9.解:∠A=29°45',则∠A的余角的度数是90°﹣29°45′=60°15'.
故答案为:60°15'.
10.解:(1)∠β的余角的大小是90°﹣41°31′=48°29′,
故答案为:48°29′;
(2)2×76°﹣(180°﹣41°31′),
=152°﹣180°+41°31′,
=13°31′.
故答案为:13°31′.
11.解:∠COD或∠BOE,∠AOC或∠BOC .
解答题:
12.解:设这个角的度数为α,
根据题意得,90°-α=(180°﹣α)-12°
解得:α=24°
余角90°﹣α=90°﹣24°=66°,
答:这个角和它的余角的度数分别为24°和66°.
13.解:(1)∵∠BAC=90°,∠ADC=90°,
∴∠B+∠C=90°,∠BAD+∠CAD=90,∠B+∠BAD=90°,∠CAD+∠C=90°,
则互余的角为:∠B和∠C,∠BAD和∠CAD,∠B和∠BAD,∠CAD和∠C;
(2)∠B=∠CAD,∠BAD=∠C.
14.解:①∠α的余角是:90°﹣∠α,∠β的补角是:180°﹣∠β;
故答案为:90°﹣∠α,180°﹣∠β;
②设∠β=x,则∠α=2x,
根据题意,得3(90°﹣2x)=180°﹣x,
解得x=18°,即∠β=18°,∠α=36°.
15.解:(1)∵∠BOD=∠COE=90°,
∴∠1+∠2=90°,∠2+∠3=90°,∠3+∠4=90°,∠1+∠4=90°,
∴∠2和∠4与∠1互余;
(2)由(1)知,∠1=∠3,∠2=∠4;
(3)由(2)知,∠1=∠3,
∴∠3的补角是∠AOE;
(4)∵∠2+∠3=90°,∠2:∠3=3:2,
∴∠3=∠1=36°,∠2=∠4=54°,
∴∠BOC=∠1+∠2+∠3=126°.
16.解:(1)∵∠AOC=64°,
∴∠AOD=180°﹣64°=116°,
∵OE平分∠AOD,
∴∠DOE=∠AOD=×116°=58°,
∵OF平分∠BOD,
∴∠DOF=∠BOD=∠AOC=×64°=32°,
∴∠EOF=∠DOE+∠DOF=58°+32°=90°;
(2)与∠AOD互补的角有∠AOC和∠BOD;
(3)与∠AOE互余的角有∠BOF和∠DOF.
17.解:(1)∵∠COD=90°,∠BOC=65°,
∴∠BOD=∠COD﹣∠BOC=25°,
∵∠AOB=90°,
∴∠AOD=∠AOB+∠BOD=90°+25°=115°;
∵∠AOD=130°,∠AOB=90°,
∴∠BOD=∠AOD﹣∠AOB=130°﹣90°=40°,
∵∠COD=90°,
∴∠BOC=∠COD﹣∠BOD=90°﹣40°=50°,
故答案为:115°,50°;
(2)∠AOD与∠BOC的数量关系是:
∠AOD+∠BOC=120°.
理由如下:
∵∠AOD+∠BOC
=∠AOD+(∠COD+∠BOD)
=∠AOD+∠COD+∠BOD
=∠COD+(∠AOD+∠BOD)
=∠COD+∠AOB,
又∠AOB=∠COD=60°,
∴∠AOD+∠BOC=60°+60°=120°;
(3)∠AOD+∠BOC=α+β,理由如下:
∵∠AOD+∠BOC
=∠AOD+(∠COD+∠BOD)
=∠AOD+∠COD+∠BOD
=∠COD+(∠AOD+∠BOD)
=∠COD+∠AOB,
又∠AOB=α,∠COD=β,
∴∠AOD+∠BOC=α+β.
1
选择题:
1.已知∠α=25°30',则它的补角为( )
A.25°30′ B.64° 30' C.164° 30' D.154°30′
2.一个角的余角是它的2倍,这个角的度数是()
A.30° B.45° C.60° D.75°
3.关于补角有下列四个叙述:①锐角的补角是钝角;②只有锐角才有补角;③互为补角的两个角不可能相等;④同角或等角的补角一定相等.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
4.如图,点O在直线AB上,∠COB=∠EOD=90°,下列说法错误的是( )
A.∠1=∠2相等 B.∠AOE与∠2互余
C.∠AOD与∠1互补 D.∠AOD与∠COD互补
5.下列说法正确的是()
A.一个角的补角一定大于它本身
B.一个角的余角一定小于它本身
C.一个钝角减去一个锐角的差一定是一个锐角
D.一个角的余角一定小于它的补角
6.若一个锐角和它的余角相等,则它的补角为( )
A.75° B.120° C.135° D.150°
7.有下列说法:
①若∠A+∠B+∠C=180°,则∠A,∠B,∠C互补;
②若∠1是∠2的余角,则∠2是∠1的余角;
③一个锐角的补角一定比它的余角大90°;
④互补的两个角中,一定是一个钝角与一个锐角.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8.互为补角的两个角的比是3:2,则较小角的余角等于( )
A.18° B.54° C.108° D.144°
填空题:
9.已知∠A=29°45',则∠A的余角的度数是 .
10.已知∠α=76°,∠β=41°31',求:
(1)∠β的余角的大小是 ;
(2)∠α的2倍与∠β的补角的差是 .
11.如图,AOB是直线,∠AOC=∠DOE=90°,则图中与∠BOD互余的角是
或 ,与∠DOE互补的角是 或 .
解答题:
12.已知一个角的余角比这个角补角的小12°,求这个角和它的余角的度数.
13.如图,已知∠BAC=90°,∠ADC=∠ADB=90°.①则图中有几对互余的角?②除直角以外,图中还有几对相等的角?说明理由.
14.①∠α的余角是 ,∠β的补角是 .
②已知∠α是∠β的2倍,∠α的余角的3倍等于∠β的补角,求∠α和∠β的度数.
15.如图,O是直线AB上的一点,∠BOD=∠COE=90°.
(1)写出图中与∠1互余的角;
(2)写出图中相等的角(直角除外);
(3)写出图中∠3的补角;
(4)若∠2:∠3=3:2,求∠BOC的度数.
16.如图,直线AB与CD相交于点O,OE平分∠AOD,OF平分∠BOD.
(1)若∠AOC=64°,求∠DOE和∠EOF的度数;
(2)写出图中与∠AOD互补的角;
(3)写出图中与∠AOE互余的角.
17.(1)如图1,∠AOB=∠COD=90°,若∠BOC=65°,则∠AOD= ;若∠AOD=130°,则∠BOC= ;
(2)如图2,∠AOB=∠COD=60°,则∠AOD与∠BOC又有怎样的数量关系,请说明理由;
(3)如图3,已知∠AOB=α,∠COD=β(α,β都是锐角),若把它们的顶点O重合一起,请直接写出∠AOD与∠BOC的数量关系,不必说明理由.
参考答案:
1.D解:180°﹣25°30′=154°30′.故选:D.
2.A解:设这个角为x度,根据 题意得:x+2x=90,解得:x=30,故这个角为30°.
3.B解:①若∠A是锐角,则180°﹣∠A>90°,即锐角的补角是钝角,那么①正确.
②任意角均有补角,那么②错误.
③直角的补角是直角,得互补的两个角也可能相等,那么③错误.
④同角或等角的补角相等,那么④正确.综上:正确的有①④,共2个.故选:B.
4.解:∵∠COB=∠EOD=90°,
∴∠1+∠COD=∠2+∠COD=90°,
∴∠1=∠2,故A选项正确;
∵∠AOE+∠1=90°,
∴∠AOE+∠2=90°,即∠AOE与∠2互余,故B选项正确;
∵∠COB=90°,
∵∠AOD+∠2=180°,
∵∠1=∠2,
∴∠AOD+∠1=180°,即∠AOD与∠1互补,故C选项正确;
无法判断∠AOD与∠COD是否互余,D选项错误;
故选:D.
5.D解:A不正确,钝角的补角是锐角小于它本身;B不正确,大于45°的角的余角就小于它本身,C不正确,例如130°减去10°的角差是120°还是钝角故正确答案是D.
6.C解:设这个角为α,它的余角也是α,则2α=90°解得:α=45°,180°-45°=135°故选C
7.B解:①补角一定指的是两个角之间的关系,错误.
②若∠1是∠2的补角,则∠2是∠1的补角,正确.
③同一个锐角的补角一定比它的余角大90°,正确,180﹣α﹣(90﹣α)=90.
④互补的两个角中,一定是一个钝角与一个锐角,错误,90°+90°=180°.
故选:B.
8.解:∵互为补角的两个角的比是3:2,
∴较大的角=180°×=108°,较小的角=180°×=72°,
∴较小角的余角=90°﹣72°=18°,
故选:A.
填空题
9.解:∠A=29°45',则∠A的余角的度数是90°﹣29°45′=60°15'.
故答案为:60°15'.
10.解:(1)∠β的余角的大小是90°﹣41°31′=48°29′,
故答案为:48°29′;
(2)2×76°﹣(180°﹣41°31′),
=152°﹣180°+41°31′,
=13°31′.
故答案为:13°31′.
11.解:∠COD或∠BOE,∠AOC或∠BOC .
解答题:
12.解:设这个角的度数为α,
根据题意得,90°-α=(180°﹣α)-12°
解得:α=24°
余角90°﹣α=90°﹣24°=66°,
答:这个角和它的余角的度数分别为24°和66°.
13.解:(1)∵∠BAC=90°,∠ADC=90°,
∴∠B+∠C=90°,∠BAD+∠CAD=90,∠B+∠BAD=90°,∠CAD+∠C=90°,
则互余的角为:∠B和∠C,∠BAD和∠CAD,∠B和∠BAD,∠CAD和∠C;
(2)∠B=∠CAD,∠BAD=∠C.
14.解:①∠α的余角是:90°﹣∠α,∠β的补角是:180°﹣∠β;
故答案为:90°﹣∠α,180°﹣∠β;
②设∠β=x,则∠α=2x,
根据题意,得3(90°﹣2x)=180°﹣x,
解得x=18°,即∠β=18°,∠α=36°.
15.解:(1)∵∠BOD=∠COE=90°,
∴∠1+∠2=90°,∠2+∠3=90°,∠3+∠4=90°,∠1+∠4=90°,
∴∠2和∠4与∠1互余;
(2)由(1)知,∠1=∠3,∠2=∠4;
(3)由(2)知,∠1=∠3,
∴∠3的补角是∠AOE;
(4)∵∠2+∠3=90°,∠2:∠3=3:2,
∴∠3=∠1=36°,∠2=∠4=54°,
∴∠BOC=∠1+∠2+∠3=126°.
16.解:(1)∵∠AOC=64°,
∴∠AOD=180°﹣64°=116°,
∵OE平分∠AOD,
∴∠DOE=∠AOD=×116°=58°,
∵OF平分∠BOD,
∴∠DOF=∠BOD=∠AOC=×64°=32°,
∴∠EOF=∠DOE+∠DOF=58°+32°=90°;
(2)与∠AOD互补的角有∠AOC和∠BOD;
(3)与∠AOE互余的角有∠BOF和∠DOF.
17.解:(1)∵∠COD=90°,∠BOC=65°,
∴∠BOD=∠COD﹣∠BOC=25°,
∵∠AOB=90°,
∴∠AOD=∠AOB+∠BOD=90°+25°=115°;
∵∠AOD=130°,∠AOB=90°,
∴∠BOD=∠AOD﹣∠AOB=130°﹣90°=40°,
∵∠COD=90°,
∴∠BOC=∠COD﹣∠BOD=90°﹣40°=50°,
故答案为:115°,50°;
(2)∠AOD与∠BOC的数量关系是:
∠AOD+∠BOC=120°.
理由如下:
∵∠AOD+∠BOC
=∠AOD+(∠COD+∠BOD)
=∠AOD+∠COD+∠BOD
=∠COD+(∠AOD+∠BOD)
=∠COD+∠AOB,
又∠AOB=∠COD=60°,
∴∠AOD+∠BOC=60°+60°=120°;
(3)∠AOD+∠BOC=α+β,理由如下:
∵∠AOD+∠BOC
=∠AOD+(∠COD+∠BOD)
=∠AOD+∠COD+∠BOD
=∠COD+(∠AOD+∠BOD)
=∠COD+∠AOB,
又∠AOB=α,∠COD=β,
∴∠AOD+∠BOC=α+β.
1
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
