初中数学人教版 九下27.2.3相似三角形应用举例 第1课时 同步检测(含解析)
文档属性
| 名称 | 初中数学人教版 九下27.2.3相似三角形应用举例 第1课时 同步检测(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 240.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 13:34:48 | ||
图片预览




文档简介
27.2.3相似三角形应用举例
一、单选题
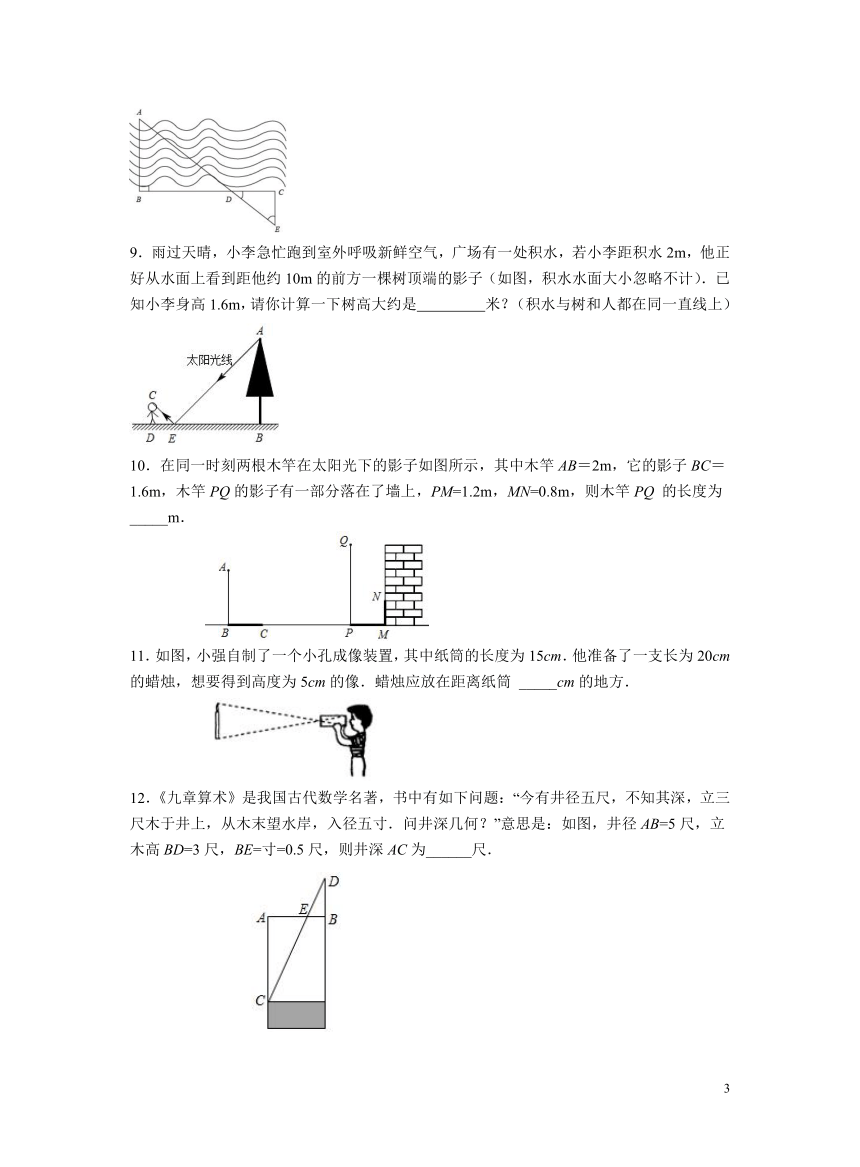
1.如图,小芳和爸爸正在散步,爸爸身高1.8米,他在地面上的影长为2.1米,若小芳身高只有1.2 m,则她的影长为( )
A.1.2m B.1.6m C. 1.4m D.1.8m
2.如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为36 cm,那么它在暗盒中所成的像CD的高度应为( )
A.16cm B. 14cm C.25cm D.32cm
3.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=30cm,EF=15cm,测得边DF离地面的高度AC=1.6m,CD=10m,则树高AB长为( )
A.21.6m B.6.6m C.20.6m D.7.6m
4.如图,图1是装了液体的高脚杯,加入一些液体后如图2所示,则此时液面AB为( )
A.5.6cm B.10cm C.8cm D. 6.4cm
5.如图,小勇在探究课本“综合与实践”中的“制作视力表”时,根据测试距离为5 m的标准视力表制作了一个测试距离为3 m的视力表.如果标准视力表中“E”的高a是72.7 mm,那么制作出的视力表中相应“E”的高b是( )
A.121.17 mm B.43.62 mm C.43.36 mm D.29.08 mm
二、填空题
6.如图,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,已知网高为0.8米,击球点到网的水平距离为3米则球拍击球的高度h为_________米.
7.如图,小红把梯子AB斜靠在墙壁上,梯脚B距墙2米,此时D点距墙1.8米,BD长0.6米,则梯子AB的长为_____米.
8. 为了估计河的宽度,我们可以在河对岸的岸边选定一个目标记为点A,再在河的这一边选点B和点C,使得AB⊥BC,设BC与AE交于点D,如图所示测BD=120m,
CD=40m,EC=30m,那么河宽 米.
9.雨过天晴,小李急忙跑到室外呼吸新鲜空气,广场有一处积水,若小李距积水2m,他正好从水面上看到距他约10m的前方一棵树顶端的影子(如图,积水水面大小忽略不计).已知小李身高1.6m,请你计算一下树高大约是 米?(积水与树和人都在同一直线上)
10.在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ 的长度为_____m.
11.如图,小强自制了一个小孔成像装置,其中纸筒的长度为15cm.他准备了一支长为20cm的蜡烛,想要得到高度为5cm的像.蜡烛应放在距离纸筒 _____cm的地方.
12.《九章算术》是我国古代数学名著,书中有如下问题:“今有井径五尺,不知其深,立三尺木于井上,从木末望水岸,入径五寸.问井深几何?”意思是:如图,井径AB=5尺,立木高BD=3尺,BE=寸=0.5尺,则井深AC为______尺.
13.如图,AB表示一个窗户的高,AM和BN表示射入室内的光线,窗户的下端到地面的距离BC=1m.已知某一时刻BC在地面的影长CN=1.5m,AC在地面的影长CM=4.5m,则窗户的高度为_________m.
三、解答题
14.如图①是公园跷跷板的示意图,立柱OC与地面垂直,点C为横板AB的中点.小明和小聪去玩跷跷板,小明最高能将小聪翘到1米高(如图②).
(1)求立柱OC的高度;
(2)小明想要把小聪最高翘到1.25米高,请你帮他找出一种方法,并解答.
参考答案
1. C
【解析】设小芳的影长为h,再根据同一时刻物高与影长成正比即可求出h的值即可.
【详解】解:设小芳的影长为h米
∵同一时刻物高与影长成正比
∴
解得h=1.4 故选C
2.A
【解析】如图,过O作OG⊥AB于G,过O作OK⊥CD于K再利用相似三角形的对应高之比等于相似比列方程,再解方程即可.
【详解】解:如图,过O作OG⊥AB于G,过O作OK⊥CD于K
由小孔成像原理可得: △AOB∽△COD
∴而
所以CD=16(cm),经检验符合题意. 故选A
【点睛】本题考查的是相似三角形的应用,相似三角形的性质,掌握“相似三角形的对应高之比等于相似比”是解本题的关键.
3.B
【解析】根据△DEF∽△DCB即可求得BC的长,进而求得树高AB
【详解】解:依题意∠EDF=∠CDB,EF⊥DE,BC⊥DC
∴∠DEF=∠DCB
∴△DEF∽△DCB
∵DE=30cm,EF=15cm,CD=10m,AC=1.6m,
m
∴AB=AC+BC=1.6+5=6.6 m 故选B
【点睛】本题考查了相似三角形的性质与判定,相似三角形的应用,根据题意找到相似三角形是解题的关键.
4.D
【解析】根据两三角形相似,列出比例式进而求解即可.
【详解】依题意,两高脚杯中的液体部分两三角形相似,则
解得AB=6.4.故选D
5.B
【解析】给图中图形标上顶点,利用三角形相似,得到对应边的比例式,最后代值即可求出高b.
【详解】解:如下图所示:
由题意可知:△ABC∽△ADE,
故有:,故选:B.
6.1.4
【解析】由于DBEC,可得△ADB∽△AEC,故可用相似三角形的性质求解.
【详解】解:如图,∵DB//EC,
∴△ADB∽△AEC,
∴即0.8×(4+3)=4h,
∴h=1.4 (m).
故答案为1.4.
7.6
【解析】根据梯子、墙、地面三者构成的直角三角形与梯子、墙、梯上点D三者构成的直角三角相似,利用相似三角形对应边成比例解答即可.
【详解】解:∵DE⊥AC,BC⊥AC,
∴∠AED=∠ACB=90°;
∴DE∥BC,
∴∠ADE=∠ABC
∴△ADE∽△ABC ,
;
设梯子AB的长为x米,
∵BC=2,DE=1.8,BD=0.6,,
∴x=6,即梯子的长度为6米.故答案为:6
8.90 m
【解析】先证明△ABD∽△ECD,然后利用相似比计算出AB的长即可.
【详解】解:∵AB⊥BC,CD⊥BC,
∴∠B=∠C=90°
又∵∠ADB=∠EDC
∴△ABD∽△ECD,
∴AB:CE=BD:CD,
即AB:30=120:40,
∴AB=90(m),
即这条河的大致宽度是90 m.
9.6.4米
【解析】根据题意得:△CDE∽△ABE,然后利用相似三角形的性质列式计算即可.【详解】解:由题意得:△CDE∽△ABE,
∴,
∵CD=1.6,DE=2,BE=8,
即: ,解得:AB=6.4,所以树高大约是6.4米.
10.2.3
【解析】过N点作ND⊥PQ于点D,根据同一时刻木竿长和影子长的比是固定的得到,求出QD的长,即可求出结果.
【详解】解:如图,过N点作ND⊥PQ于点D,
则四边形DPMN是矩形,
∴DN=PM
根据同一时刻木竿长和影子长的比是固定的,
∴,
∵AB=2m,BC=1.6m,PM=1.2m,MN=0.8m,
∴,
∴PQ=QD+DP=QD+MN=1.5+0.8=2.3m.
11.60
【解析】先根据题意得出相似三角形,再利用三角形相似的性质得到相似比,然后根据比例性质计算.
【详解】解:如图,AB=20 cm,OF=15 cm,CD=5 cm,
∵AB∥CD,EF⊥AB,
∴EF⊥CD,
∴△OAB∽△ODC,
∴
解得OE=60 cm.
答:蜡烛应放在距离纸筒60 cm的地方.故答案为:60.
12.27
【解析】根据AC∥BD,得到△ACE∽△BDE,进而得到,代入数值,求出AC,问题得解.
【详解】解:∵AC∥BD,
∴△ACE∽△BDE,
∴,
即,
解得AC=27,
故井深AC为27尺.
故答案为:27
13.2
【解析】阳光可认为是一束平行光,由光的直线传播特性可知透过窗户后的光线BN与AM仍然平行,由此可得出一对相似三角形,由相似三角形性质可进一步求出AB的长,即窗户的高度.
【详解】解:∵BN∥AM,
∴△CBN∽△CAM,
∴,
∵CN=1.5,CM=4.5,BC=1,
∴,
∴AC=3,
∴AB=AC-BC=2m,
答:窗户的高度AB是2m.
14.(1)0.5米
(2)设计方法为:要使小明想要把小聪最高翘到1.25米高,只需要将小明距离点O的距离变为0.4BD,即BO=0.4BD
【解析】(1)标注点D,根据题意证明出Rt△ABD∽Rt△CBO,得到,再根据C,O分别为AB,BD的中点,即可得到;
(2)利用三角形相似来设计,同样先证明Rt△ABD∽Rt△CBO,得,根据AD=1.25,CO=0.5,找到BD,BO之间的关系即可.
(1)解:标注点D如下图:
根据题意在Rt△ABD和Rt△CBO中
∵∠B=∠B,∠ADB=∠COB=90°,
∴Rt△ABD∽Rt△CBO,
,
分别为AB的中点,
,
,
∴OC=0.5(米);
(2)解:设计方法为:要使小明想要把小聪最高翘到1.25米高,只需要将小明距离点O的距离变为0.4BD ,即BO=0.4BD,过程如下:
根据题意作如下图形,
根据题意在Rt△ABD和Rt△CBO,
∵∠B=∠B,∠ADB=∠COB=90°,
∴Rt△ABD∽Rt△CBO,
,
∵AD=1.25,CO=0.5,
,
∴BO=0.4BD(米);
∴小明想要把小聪最高翘到1.25米高,只需要将小明距离点O的距离变为0.4BD,即BO=0.4BD即可.
1
一、单选题
1.如图,小芳和爸爸正在散步,爸爸身高1.8米,他在地面上的影长为2.1米,若小芳身高只有1.2 m,则她的影长为( )
A.1.2m B.1.6m C. 1.4m D.1.8m
2.如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为36 cm,那么它在暗盒中所成的像CD的高度应为( )
A.16cm B. 14cm C.25cm D.32cm
3.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=30cm,EF=15cm,测得边DF离地面的高度AC=1.6m,CD=10m,则树高AB长为( )
A.21.6m B.6.6m C.20.6m D.7.6m
4.如图,图1是装了液体的高脚杯,加入一些液体后如图2所示,则此时液面AB为( )
A.5.6cm B.10cm C.8cm D. 6.4cm
5.如图,小勇在探究课本“综合与实践”中的“制作视力表”时,根据测试距离为5 m的标准视力表制作了一个测试距离为3 m的视力表.如果标准视力表中“E”的高a是72.7 mm,那么制作出的视力表中相应“E”的高b是( )
A.121.17 mm B.43.62 mm C.43.36 mm D.29.08 mm
二、填空题
6.如图,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,已知网高为0.8米,击球点到网的水平距离为3米则球拍击球的高度h为_________米.
7.如图,小红把梯子AB斜靠在墙壁上,梯脚B距墙2米,此时D点距墙1.8米,BD长0.6米,则梯子AB的长为_____米.
8. 为了估计河的宽度,我们可以在河对岸的岸边选定一个目标记为点A,再在河的这一边选点B和点C,使得AB⊥BC,设BC与AE交于点D,如图所示测BD=120m,
CD=40m,EC=30m,那么河宽 米.
9.雨过天晴,小李急忙跑到室外呼吸新鲜空气,广场有一处积水,若小李距积水2m,他正好从水面上看到距他约10m的前方一棵树顶端的影子(如图,积水水面大小忽略不计).已知小李身高1.6m,请你计算一下树高大约是 米?(积水与树和人都在同一直线上)
10.在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ 的长度为_____m.
11.如图,小强自制了一个小孔成像装置,其中纸筒的长度为15cm.他准备了一支长为20cm的蜡烛,想要得到高度为5cm的像.蜡烛应放在距离纸筒 _____cm的地方.
12.《九章算术》是我国古代数学名著,书中有如下问题:“今有井径五尺,不知其深,立三尺木于井上,从木末望水岸,入径五寸.问井深几何?”意思是:如图,井径AB=5尺,立木高BD=3尺,BE=寸=0.5尺,则井深AC为______尺.
13.如图,AB表示一个窗户的高,AM和BN表示射入室内的光线,窗户的下端到地面的距离BC=1m.已知某一时刻BC在地面的影长CN=1.5m,AC在地面的影长CM=4.5m,则窗户的高度为_________m.
三、解答题
14.如图①是公园跷跷板的示意图,立柱OC与地面垂直,点C为横板AB的中点.小明和小聪去玩跷跷板,小明最高能将小聪翘到1米高(如图②).
(1)求立柱OC的高度;
(2)小明想要把小聪最高翘到1.25米高,请你帮他找出一种方法,并解答.
参考答案
1. C
【解析】设小芳的影长为h,再根据同一时刻物高与影长成正比即可求出h的值即可.
【详解】解:设小芳的影长为h米
∵同一时刻物高与影长成正比
∴
解得h=1.4 故选C
2.A
【解析】如图,过O作OG⊥AB于G,过O作OK⊥CD于K再利用相似三角形的对应高之比等于相似比列方程,再解方程即可.
【详解】解:如图,过O作OG⊥AB于G,过O作OK⊥CD于K
由小孔成像原理可得: △AOB∽△COD
∴而
所以CD=16(cm),经检验符合题意. 故选A
【点睛】本题考查的是相似三角形的应用,相似三角形的性质,掌握“相似三角形的对应高之比等于相似比”是解本题的关键.
3.B
【解析】根据△DEF∽△DCB即可求得BC的长,进而求得树高AB
【详解】解:依题意∠EDF=∠CDB,EF⊥DE,BC⊥DC
∴∠DEF=∠DCB
∴△DEF∽△DCB
∵DE=30cm,EF=15cm,CD=10m,AC=1.6m,
m
∴AB=AC+BC=1.6+5=6.6 m 故选B
【点睛】本题考查了相似三角形的性质与判定,相似三角形的应用,根据题意找到相似三角形是解题的关键.
4.D
【解析】根据两三角形相似,列出比例式进而求解即可.
【详解】依题意,两高脚杯中的液体部分两三角形相似,则
解得AB=6.4.故选D
5.B
【解析】给图中图形标上顶点,利用三角形相似,得到对应边的比例式,最后代值即可求出高b.
【详解】解:如下图所示:
由题意可知:△ABC∽△ADE,
故有:,故选:B.
6.1.4
【解析】由于DBEC,可得△ADB∽△AEC,故可用相似三角形的性质求解.
【详解】解:如图,∵DB//EC,
∴△ADB∽△AEC,
∴即0.8×(4+3)=4h,
∴h=1.4 (m).
故答案为1.4.
7.6
【解析】根据梯子、墙、地面三者构成的直角三角形与梯子、墙、梯上点D三者构成的直角三角相似,利用相似三角形对应边成比例解答即可.
【详解】解:∵DE⊥AC,BC⊥AC,
∴∠AED=∠ACB=90°;
∴DE∥BC,
∴∠ADE=∠ABC
∴△ADE∽△ABC ,
;
设梯子AB的长为x米,
∵BC=2,DE=1.8,BD=0.6,,
∴x=6,即梯子的长度为6米.故答案为:6
8.90 m
【解析】先证明△ABD∽△ECD,然后利用相似比计算出AB的长即可.
【详解】解:∵AB⊥BC,CD⊥BC,
∴∠B=∠C=90°
又∵∠ADB=∠EDC
∴△ABD∽△ECD,
∴AB:CE=BD:CD,
即AB:30=120:40,
∴AB=90(m),
即这条河的大致宽度是90 m.
9.6.4米
【解析】根据题意得:△CDE∽△ABE,然后利用相似三角形的性质列式计算即可.【详解】解:由题意得:△CDE∽△ABE,
∴,
∵CD=1.6,DE=2,BE=8,
即: ,解得:AB=6.4,所以树高大约是6.4米.
10.2.3
【解析】过N点作ND⊥PQ于点D,根据同一时刻木竿长和影子长的比是固定的得到,求出QD的长,即可求出结果.
【详解】解:如图,过N点作ND⊥PQ于点D,
则四边形DPMN是矩形,
∴DN=PM
根据同一时刻木竿长和影子长的比是固定的,
∴,
∵AB=2m,BC=1.6m,PM=1.2m,MN=0.8m,
∴,
∴PQ=QD+DP=QD+MN=1.5+0.8=2.3m.
11.60
【解析】先根据题意得出相似三角形,再利用三角形相似的性质得到相似比,然后根据比例性质计算.
【详解】解:如图,AB=20 cm,OF=15 cm,CD=5 cm,
∵AB∥CD,EF⊥AB,
∴EF⊥CD,
∴△OAB∽△ODC,
∴
解得OE=60 cm.
答:蜡烛应放在距离纸筒60 cm的地方.故答案为:60.
12.27
【解析】根据AC∥BD,得到△ACE∽△BDE,进而得到,代入数值,求出AC,问题得解.
【详解】解:∵AC∥BD,
∴△ACE∽△BDE,
∴,
即,
解得AC=27,
故井深AC为27尺.
故答案为:27
13.2
【解析】阳光可认为是一束平行光,由光的直线传播特性可知透过窗户后的光线BN与AM仍然平行,由此可得出一对相似三角形,由相似三角形性质可进一步求出AB的长,即窗户的高度.
【详解】解:∵BN∥AM,
∴△CBN∽△CAM,
∴,
∵CN=1.5,CM=4.5,BC=1,
∴,
∴AC=3,
∴AB=AC-BC=2m,
答:窗户的高度AB是2m.
14.(1)0.5米
(2)设计方法为:要使小明想要把小聪最高翘到1.25米高,只需要将小明距离点O的距离变为0.4BD,即BO=0.4BD
【解析】(1)标注点D,根据题意证明出Rt△ABD∽Rt△CBO,得到,再根据C,O分别为AB,BD的中点,即可得到;
(2)利用三角形相似来设计,同样先证明Rt△ABD∽Rt△CBO,得,根据AD=1.25,CO=0.5,找到BD,BO之间的关系即可.
(1)解:标注点D如下图:
根据题意在Rt△ABD和Rt△CBO中
∵∠B=∠B,∠ADB=∠COB=90°,
∴Rt△ABD∽Rt△CBO,
,
分别为AB的中点,
,
,
∴OC=0.5(米);
(2)解:设计方法为:要使小明想要把小聪最高翘到1.25米高,只需要将小明距离点O的距离变为0.4BD ,即BO=0.4BD,过程如下:
根据题意作如下图形,
根据题意在Rt△ABD和Rt△CBO,
∵∠B=∠B,∠ADB=∠COB=90°,
∴Rt△ABD∽Rt△CBO,
,
∵AD=1.25,CO=0.5,
,
∴BO=0.4BD(米);
∴小明想要把小聪最高翘到1.25米高,只需要将小明距离点O的距离变为0.4BD,即BO=0.4BD即可.
1
