初中数学人教版八上11.2.2三角形的外角 教案
文档属性
| 名称 | 初中数学人教版八上11.2.2三角形的外角 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 201.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 13:45:45 | ||
图片预览



文档简介
11.2.2三角形的外角
【教学目标】
1.理解并掌握三角形的外角的概念;能够在能够复杂图形中找出外角;
2.掌握三角形的一个外角等于与它不相邻的两个内角的和及三角形的内角和;
3.会利用三角形的外角性质解决问题.
【教学重难点】
重点:掌握三角形的一个外角等于与它不相邻的两个内角的和及三角形的内角和.
难点:会利用三角形的外角性质解决问题.
【教学方法】
归纳推理法、小组互助法.
【教学过程】
新课导入:
创设情境,提出问题:
1.什么是三角形的内角?其内角和等于多少?
(三角形三个内角的度数和;三角形的内角和为180°.)
2.在△ABC中,∠A=80°, ∠B=52°,则∠C=______.
3.小蚂蚁先从A处爬行到C处取食物,再折到B处沿大道回家,已知∠BAC=40° , ∠ABC=70°.小蚂蚁从C处要转多少度角才能直达B处?
新课讲授:
三角形的外角
大胆尝试:
你会利用“三角形的内角和为180°”来计算∠BCD吗?
解:由三角形内角和得∠BCA=180°-∠A-∠ABC=70°,所以∠BCD=180°-∠BCA=110°.
猜想像∠BCD这样的角有什么特征呢?
通过下面的练习验证猜想:
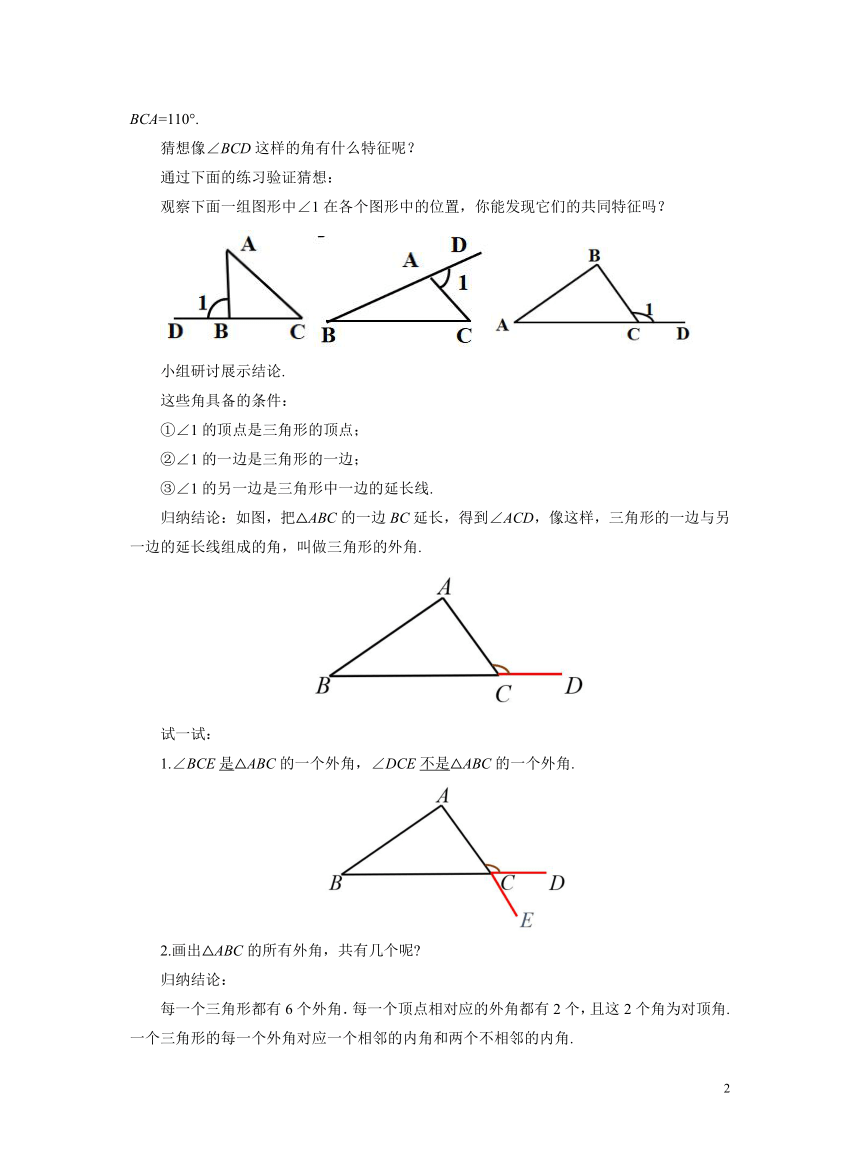
观察下面一组图形中∠1在各个图形中的位置,你能发现它们的共同特征吗?
小组研讨展示结论.
这些角具备的条件:
①∠1的顶点是三角形的顶点;
②∠1的一边是三角形的一边;
③∠1的另一边是三角形中一边的延长线.
归纳结论:如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
试一试:
1.∠BCE是△ABC的一个外角,∠DCE不是△ABC的一个外角.
2.画出△ABC的所有外角,共有几个呢
归纳结论:
每一个三角形都有6个外角.每一个顶点相对应的外角都有2个,且这2个角为对顶角.一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角.
课堂练习:
如图,∠ BEC是哪个三角形的外角?∠AEC是哪个三角形的外角?∠EFD是哪个三角形的外角?
解:∠BEC是△AEC的外角;∠AEC是△BEC的外角;∠EFD是△BEF和△DCF的外角.
(二)三角形外角的性质
思考: 如图,△ABC的外角∠BCD与其相邻的内角∠ACB有什么关系?与不相邻的内角呢?
答:∠BCD与∠ACB互补.∠BCD=∠A+∠B.
任意三角形的一个外角是否都和与它不相邻的两个内角的和相等?
方法一:
证明:∠A+∠B+∠ACB=180°,∠BCD+∠ACB=180°,
∴∠A+∠B=∠BCD.
方法二:
证明:过C作CE //AB
∴∠A=∠ECD,
∠B=∠BCE,∠BCD=∠ECD+∠BCE=∠A+∠B.
归纳结论:
三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角的和.
几何语言:
∵∠CAD是三角形ABC的外角
∴∠B+∠C=∠CAD
课堂练习:
练一练:说出下列图形中∠1和∠2的度数:
解:(1)∠1=40 °, ∠2=140 °(2)∠1=18 °, ∠2=130 °
例1:已知:如图,在△ABC中, ∠1是它的一个外角, E为边AC上一点,延长BC到D,连接DE.
试说明∠1和∠2的大小关系.
解:∵ ∠1是△ABC的一个外角,∴ ∠1=∠3+∠4,∠1>∠3.
∵∠3是△CDE的一个外角 ,∴∠3=∠2+∠5,∠3>∠2.
∴ ∠1>∠2.
例2: 如图,∠A=42°,∠ABD=28°,∠ACE=18°,求∠BFC的度数.
解:∵ ∠BEC是△AEC的一个外角,
∴ ∠BEC= ∠A+ ∠ACE,
∵∠A=42° ,∠ACE=18°,∴ ∠BEC=60°.
∵ ∠BFC是△BEF的一个外角,∴ ∠BFC= ∠ABD+ ∠BEF,
∵ ∠ABD=28° ,∠BEC=60°,∴ ∠BFC=88°.
课堂练习:
如图,P为△ABC内一点,∠BPC=150°,∠ABP=20°,∠ACP=30°,求∠A的度数.
解:延长BP交AC于点E,
则∠BPC,∠PEC分别为△PCE,△ABE的外角,
∴∠BPC=∠PEC+∠PCE,
∠PEC=∠ABE+∠A,
∴∠PEC=∠BPC-∠PCE=150°-30°=120°.
∴∠A=∠PEC-∠ABE=120°-20°=100°.
例3:如图, ∠BAE, ∠CBF, ∠ACD是△ABC的三个外角,它们的和是多少?
解法一:解:由三角形的一个外角等于与它不相邻的两个内角的和,得
∠BAE= ∠2+ ∠3,
∠CBF= ∠1+ ∠3,
∠ACD= ∠1+ ∠2.
又知∠1+ ∠2+ ∠3=180 °,
所以∠BAE+ ∠CBF+ ∠ACD=2(∠1+ ∠2+ ∠3)=360 °.
解法二:如图,∠BAE+∠1=180 ° ① ,
∠CBF +∠2=180 ° ②,
∠ACD +∠3=180 ° ③,
又知∠1+ ∠2+ ∠3=180 °,
①+ ②+ ③得
∠BAE+ ∠CBF+ ∠ACD+(∠1+ ∠2+ ∠3)=540 °,
所以∠BAE+ ∠CBF+ ∠ACD=540 °-180°=360°.
归纳结论:
从与每一个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和。
三角形的外角和等于360
(三)三角形外角的性质应用
例3:一个零件的形状如图,按规定∠A应等于90°,∠B、∠D应分别是30°和20°,李叔叔量得∠BCD=142°,就断定这个零件不合格,你能说出道理吗?
解法1:延长BC交AD于点E,
∵∠A=90°,∠B=30°,
在△ABE中,∠DEB=∠A+∠B=120°,
在△CDE中,∠DCB=∠DEB+∠D=120°+20°=140°.
若零件合格,∠DCB应等于140°.李叔叔量得∠BCD=142°,因此可以断定该零件不合格.
解法2:连接AC并延长至E,
∵∠DAB=90°,∠B=30°,∠D=20°
在△ADC中∠3=∠1+∠D
在△ACB中∠4=∠2+∠B
∠ DCB=∠3+∠4=∠1+∠D+∠2+∠B=140°
若零件合格,∠DCB应等于140°.李叔叔量得∠BCD=142°,因此可以断定该零件不合格.
课堂练习:
∠A+∠B+∠C+∠D+∠E+∠F= .
2.如图,直线AB∥CD,直线EF分别与AB、CD相交,则有( )
A.∠1+∠2-∠3=180° B .∠1-∠2+∠3=180°
C.∠3+∠2-∠1=180° D.∠1+∠2+∠3=180°
课堂小结:
本节课主要学习了两部分内容:
三角形外角的概念,三角形外角的性质.
作业布置:
1.如图,AB//CD,∠A=37°, ∠C=63°,那么∠F等于( )
A.26° B.63° C.37° D.60°
2.等腰三角形的一个外角是100°,它的各个内角度数分别是 .
3.类比三角形的内角和的证明方法证明三角形的外角和.
4.分别用三角形内角和定理和作“平行线”平移角的方法证明例题3.
【板书设计】
三角形的外角:
角一边必须是三角形的一边,另一边必须是三角形另一边的延长线.
三角形的外角的性质:
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的外角和等于360 °.
【课后反思】
创设情境,循序渐进的由旧知建立生长点的过渡到新知,用描图的方法发展学生的图形推理思维能力,培养学生形成良好的几何推理习惯.通过一题多解培养学生变通解题的能力.
1
【教学目标】
1.理解并掌握三角形的外角的概念;能够在能够复杂图形中找出外角;
2.掌握三角形的一个外角等于与它不相邻的两个内角的和及三角形的内角和;
3.会利用三角形的外角性质解决问题.
【教学重难点】
重点:掌握三角形的一个外角等于与它不相邻的两个内角的和及三角形的内角和.
难点:会利用三角形的外角性质解决问题.
【教学方法】
归纳推理法、小组互助法.
【教学过程】
新课导入:
创设情境,提出问题:
1.什么是三角形的内角?其内角和等于多少?
(三角形三个内角的度数和;三角形的内角和为180°.)
2.在△ABC中,∠A=80°, ∠B=52°,则∠C=______.
3.小蚂蚁先从A处爬行到C处取食物,再折到B处沿大道回家,已知∠BAC=40° , ∠ABC=70°.小蚂蚁从C处要转多少度角才能直达B处?
新课讲授:
三角形的外角
大胆尝试:
你会利用“三角形的内角和为180°”来计算∠BCD吗?
解:由三角形内角和得∠BCA=180°-∠A-∠ABC=70°,所以∠BCD=180°-∠BCA=110°.
猜想像∠BCD这样的角有什么特征呢?
通过下面的练习验证猜想:
观察下面一组图形中∠1在各个图形中的位置,你能发现它们的共同特征吗?
小组研讨展示结论.
这些角具备的条件:
①∠1的顶点是三角形的顶点;
②∠1的一边是三角形的一边;
③∠1的另一边是三角形中一边的延长线.
归纳结论:如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
试一试:
1.∠BCE是△ABC的一个外角,∠DCE不是△ABC的一个外角.
2.画出△ABC的所有外角,共有几个呢
归纳结论:
每一个三角形都有6个外角.每一个顶点相对应的外角都有2个,且这2个角为对顶角.一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角.
课堂练习:
如图,∠ BEC是哪个三角形的外角?∠AEC是哪个三角形的外角?∠EFD是哪个三角形的外角?
解:∠BEC是△AEC的外角;∠AEC是△BEC的外角;∠EFD是△BEF和△DCF的外角.
(二)三角形外角的性质
思考: 如图,△ABC的外角∠BCD与其相邻的内角∠ACB有什么关系?与不相邻的内角呢?
答:∠BCD与∠ACB互补.∠BCD=∠A+∠B.
任意三角形的一个外角是否都和与它不相邻的两个内角的和相等?
方法一:
证明:∠A+∠B+∠ACB=180°,∠BCD+∠ACB=180°,
∴∠A+∠B=∠BCD.
方法二:
证明:过C作CE //AB
∴∠A=∠ECD,
∠B=∠BCE,∠BCD=∠ECD+∠BCE=∠A+∠B.
归纳结论:
三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角的和.
几何语言:
∵∠CAD是三角形ABC的外角
∴∠B+∠C=∠CAD
课堂练习:
练一练:说出下列图形中∠1和∠2的度数:
解:(1)∠1=40 °, ∠2=140 °(2)∠1=18 °, ∠2=130 °
例1:已知:如图,在△ABC中, ∠1是它的一个外角, E为边AC上一点,延长BC到D,连接DE.
试说明∠1和∠2的大小关系.
解:∵ ∠1是△ABC的一个外角,∴ ∠1=∠3+∠4,∠1>∠3.
∵∠3是△CDE的一个外角 ,∴∠3=∠2+∠5,∠3>∠2.
∴ ∠1>∠2.
例2: 如图,∠A=42°,∠ABD=28°,∠ACE=18°,求∠BFC的度数.
解:∵ ∠BEC是△AEC的一个外角,
∴ ∠BEC= ∠A+ ∠ACE,
∵∠A=42° ,∠ACE=18°,∴ ∠BEC=60°.
∵ ∠BFC是△BEF的一个外角,∴ ∠BFC= ∠ABD+ ∠BEF,
∵ ∠ABD=28° ,∠BEC=60°,∴ ∠BFC=88°.
课堂练习:
如图,P为△ABC内一点,∠BPC=150°,∠ABP=20°,∠ACP=30°,求∠A的度数.
解:延长BP交AC于点E,
则∠BPC,∠PEC分别为△PCE,△ABE的外角,
∴∠BPC=∠PEC+∠PCE,
∠PEC=∠ABE+∠A,
∴∠PEC=∠BPC-∠PCE=150°-30°=120°.
∴∠A=∠PEC-∠ABE=120°-20°=100°.
例3:如图, ∠BAE, ∠CBF, ∠ACD是△ABC的三个外角,它们的和是多少?
解法一:解:由三角形的一个外角等于与它不相邻的两个内角的和,得
∠BAE= ∠2+ ∠3,
∠CBF= ∠1+ ∠3,
∠ACD= ∠1+ ∠2.
又知∠1+ ∠2+ ∠3=180 °,
所以∠BAE+ ∠CBF+ ∠ACD=2(∠1+ ∠2+ ∠3)=360 °.
解法二:如图,∠BAE+∠1=180 ° ① ,
∠CBF +∠2=180 ° ②,
∠ACD +∠3=180 ° ③,
又知∠1+ ∠2+ ∠3=180 °,
①+ ②+ ③得
∠BAE+ ∠CBF+ ∠ACD+(∠1+ ∠2+ ∠3)=540 °,
所以∠BAE+ ∠CBF+ ∠ACD=540 °-180°=360°.
归纳结论:
从与每一个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和。
三角形的外角和等于360
(三)三角形外角的性质应用
例3:一个零件的形状如图,按规定∠A应等于90°,∠B、∠D应分别是30°和20°,李叔叔量得∠BCD=142°,就断定这个零件不合格,你能说出道理吗?
解法1:延长BC交AD于点E,
∵∠A=90°,∠B=30°,
在△ABE中,∠DEB=∠A+∠B=120°,
在△CDE中,∠DCB=∠DEB+∠D=120°+20°=140°.
若零件合格,∠DCB应等于140°.李叔叔量得∠BCD=142°,因此可以断定该零件不合格.
解法2:连接AC并延长至E,
∵∠DAB=90°,∠B=30°,∠D=20°
在△ADC中∠3=∠1+∠D
在△ACB中∠4=∠2+∠B
∠ DCB=∠3+∠4=∠1+∠D+∠2+∠B=140°
若零件合格,∠DCB应等于140°.李叔叔量得∠BCD=142°,因此可以断定该零件不合格.
课堂练习:
∠A+∠B+∠C+∠D+∠E+∠F= .
2.如图,直线AB∥CD,直线EF分别与AB、CD相交,则有( )
A.∠1+∠2-∠3=180° B .∠1-∠2+∠3=180°
C.∠3+∠2-∠1=180° D.∠1+∠2+∠3=180°
课堂小结:
本节课主要学习了两部分内容:
三角形外角的概念,三角形外角的性质.
作业布置:
1.如图,AB//CD,∠A=37°, ∠C=63°,那么∠F等于( )
A.26° B.63° C.37° D.60°
2.等腰三角形的一个外角是100°,它的各个内角度数分别是 .
3.类比三角形的内角和的证明方法证明三角形的外角和.
4.分别用三角形内角和定理和作“平行线”平移角的方法证明例题3.
【板书设计】
三角形的外角:
角一边必须是三角形的一边,另一边必须是三角形另一边的延长线.
三角形的外角的性质:
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的外角和等于360 °.
【课后反思】
创设情境,循序渐进的由旧知建立生长点的过渡到新知,用描图的方法发展学生的图形推理思维能力,培养学生形成良好的几何推理习惯.通过一题多解培养学生变通解题的能力.
1
