初中数学人教版八上11.2.2三角形的外角 习题(含解析)
文档属性
| 名称 | 初中数学人教版八上11.2.2三角形的外角 习题(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 155.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 13:36:57 | ||
图片预览




文档简介
11.2.2三角形的外角
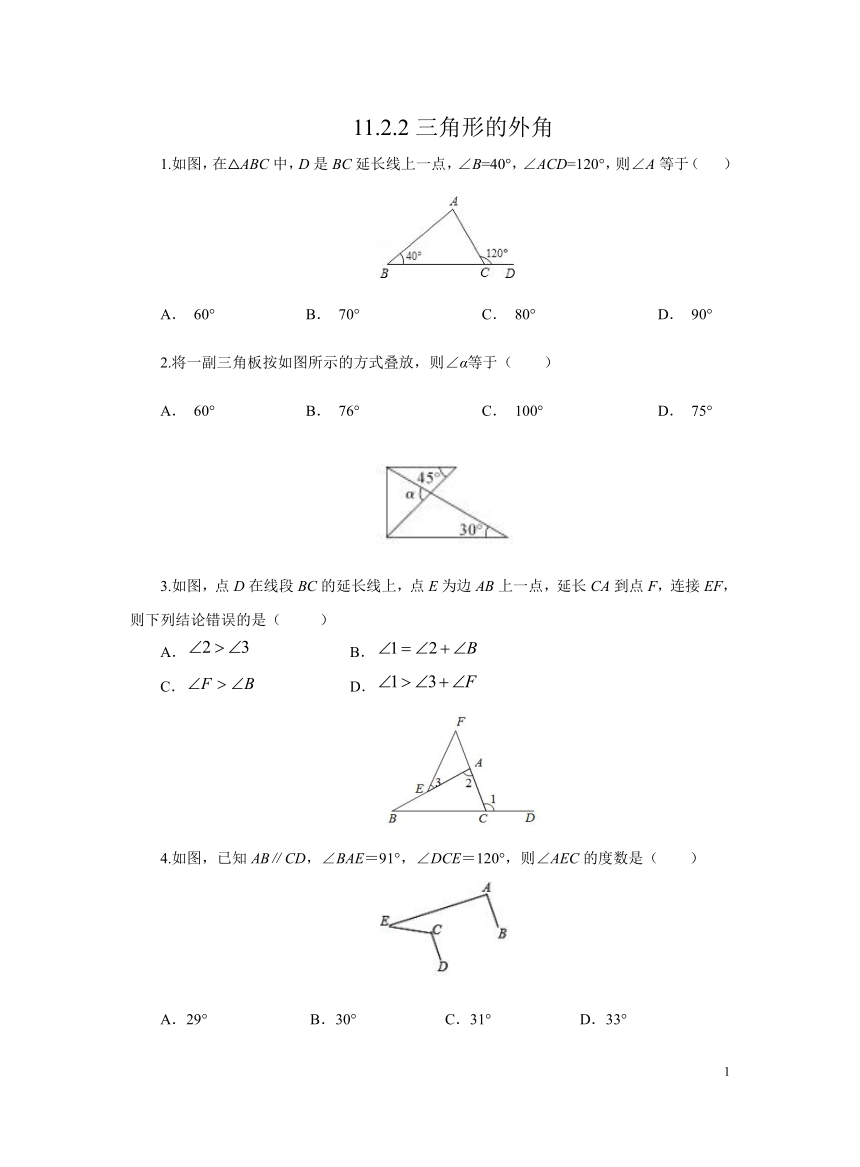
1.如图,在△ABC中,D是BC延长线上一点,∠B=40°,∠ACD=120°,则∠A等于( )
A. 60° B. 70° C. 80° D. 90°
2.将一副三角板按如图所示的方式叠放,则∠α等于( )
A. 60° B. 76° C. 100° D. 75°
3.如图,点D在线段BC的延长线上,点E为边AB上一点,延长CA到点F,连接EF,则下列结论错误的是( )
A. B.
C. D.
4.如图,已知AB∥CD,∠BAE=91°,∠DCE=120°,则∠AEC的度数是( )
A.29° B.30° C.31° D.33°
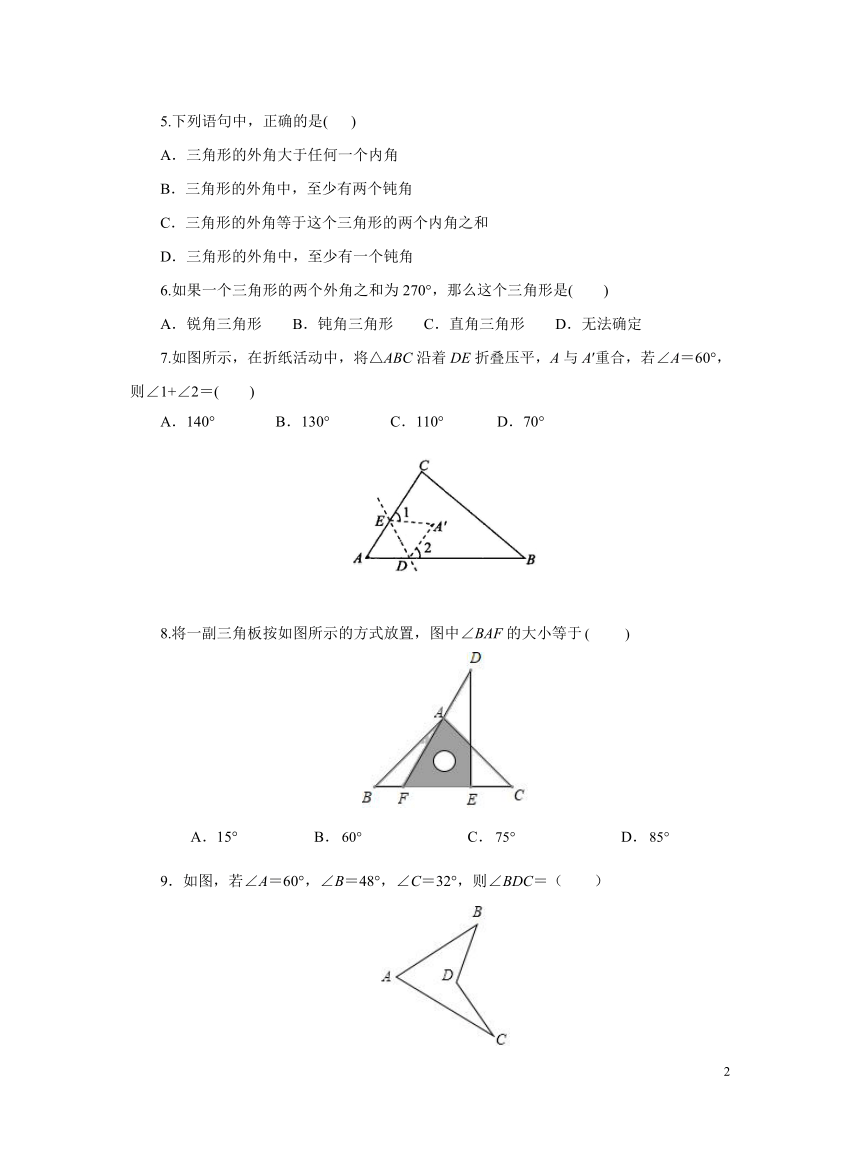
5.下列语句中,正确的是( )
A.三角形的外角大于任何一个内角
B.三角形的外角中,至少有两个钝角
C.三角形的外角等于这个三角形的两个内角之和
D.三角形的外角中,至少有一个钝角
6.如果一个三角形的两个外角之和为270°,那么这个三角形是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.无法确定
7.如图所示,在折纸活动中,将△ABC沿着DE折叠压平,A与A′重合,若∠A=60°,则∠1+∠2=( )
A.140° B.130° C.110° D.70°
8.将一副三角板按如图所示的方式放置,图中∠BAF的大小等于
A.15° B. C. D.
9.如图,若∠A=60°,∠B=48°,∠C=32°,则∠BDC=( )
A.102° B.160° C.150° D.140°
10.根据如图所示角的度数,求出其中∠α的度数.
(1)α= , (2)α= ,(3)α= .
11.已知:如图,AB∥EF,∠ABC=80°,∠CDF=140°,求的度数.
12.如图,∠ABD,∠ACD的角平分线交于点P,若∠A=55°,∠D=15°,求∠P的度数.
13.如图所示,在△ABC中,∠1=∠2,∠C>∠B,点E在AD的延长线上,且EF⊥BC于F.试探索∠DEF与∠B,∠C的大小关系;
14.如图,在△ABC中,∠B=30°,∠BAC=90°,点P是BC的动点(不与点B,C重合),AI、CI分别是∠PAC和∠PCA的角平分线,∠AIC的取值范围为m<∠AIC15.如图,在△ABC中,∠B=∠C=50°,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连结DE.
(1)当∠BAD=70°,求∠CDE的度数;
(2)当点D在BC(点B、C除外)边上运动时,试写出∠BAD与∠CDE的数量关系,并说明理由.
参考答案
1.C
解:∵∠ACD=120°,∠B=40°,
∴∠A=∠ACD-∠B=120°-40°=80°.
2.D
解析:根据三角板的特点,可知∠1=45°,然后根据三角形的外角,可求∠α=75°.
3.C
解:∵,
∴,故A选项正确,不符合题意;
由三角形外角性质即可直接得出,故B选项正确,不符合题意;
没有条件可以证明出和的关系,故C选项错误,符合题意;
∵,,
∴,
∴,故D选项正确,不符合题意;
A
解:延长DC,交AE于点M,如图所示:
∴AB∥CD,
∴∠CME=∠BAE=91°,
∴∠AEC=∠DCE﹣∠CME=10°﹣91°=29°.
B
解:因为三角形的内角中最多有一个钝角,所以外角中最多有一个锐角,即外角中至少有两个钝角.
C
解:因为三角形的外角和360°,而两个外角的和为270°,所以另一个外角为90°,所以与这个外角相邻的内有为90°.
C
解:如图,连接AA',∠1=∠3+∠4,∠2=∠5+∠6,
∴∠1+∠2=∠3+∠4+∠5+∠6=∠DAE+∠DA'E=120°,
8. A
解:∵∠DAC=∠DFE+∠C=60°+45°=105°,
∴∠CAF=180°-∠DAC=75°,
∴∠BAF=90°-∠CAF=15°
9. D
解:如图,延长AD,
∵∠1=∠B+∠BAD,∠2=∠C+∠CAD,∠A=60°,∠B=48°,∠C=32°,
∴∠1+∠2=∠B+∠C+∠BAC=48°+32°+60°=140°.
10. (1)48°; (2)27°; (3)85°;
解:(1)α=120°-72°=48°;
(2)48°+ α=20°+55°,α=27°;
(3)α=40°+25°+20°=85°.
11. 40°
解:∠EDC=180°-∠CDF=180°-140°=40°,
∵AB∥EF,∠ABC=80°,
∴∠EGC=∠ABC=80°,
又∵∠EGC=∠BCD+∠EDC,
∴∠BCD=80°-40°=40°.
12. 解:延长PC交BD于E,设AC、PB交于F,
∵∠A+∠ABF+∠AFB=∠P+∠PCF+∠PFC=180°,
∵∠AFB=∠PFC,
∴∠P+∠PCF=∠A+∠ABF,
∵∠P+∠PBE=∠PED,∠PED=∠PCD﹣∠D,
∴∠P+∠PBE=∠PCD﹣∠D,
∴2∠P+∠PCF+∠PBE=∠A﹣∠D+∠ABF+∠PCD,
∵PB、PC是角平分线
∴∠PCF=∠PCD,∠ABF=∠PBE,
∴2∠P=∠A﹣∠D
∵∠A=55°,∠D=15°,
∴∠P=20°.
13. 解:∵ ∠BAC=180°-(∠B+∠C), ∠1=∠2,
∴ ∠1=∠BAC=[180°-(∠B+∠C)]=90°-(∠B+∠C).
∴ ∠EDF=∠B+∠1=∠B+90°-(∠B+∠C)=90°+(∠B-∠C).
又∵ EF⊥BC,∴ ∠EFD=90°.
∴ ∠DEF=90°-∠EDF=90°-[90°+(∠B-∠C)]=(∠C-∠B).
14. 105°,150°
解:如图:延长AI交BC于点D,
∵∠BAC=90°,∠B=30°,
∴∠PCA=60°,∠PAC<90°,
∵AI、CI分别平分∠PAC,∠PCA,
∴∠IAC=∠PAC<45°,∠BAD>45°,∠PCI=∠ICA=∠PCA=30°,
∴∠IAC=180°-∠AIC-∠ICA,
∴180°-∠AIC-∠ICA<45°,
∴∠AIC>105°,
∵∠AIC=∠IDC+∠ICP=∠BAD+∠B+∠PCI,
∠BAD>45°,
∴∠BAD=∠AIC-∠B-∠PCI>45°,
∴∠AIC>135°,
∴105°<∠AIC<150°,
∴m=105°,n=150°.
15. 解:(1)∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=70°+50°=120°,
∵∠AED是△CDE的外角,
∴∠AED=∠C+∠EDC.
∵∠B=∠C,∠ADE=∠AED,
∴∠ADC-∠EDC=∠EDC+∠C,
∴120°-∠EDC=50°+∠EDC,
解得:∠CDE=35°;
(2)∠CDE=∠BAD,
理由:∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD,
∵∠AED是△CDE的外角,
∴∠AED=∠C+∠CDE,
∵∠B=∠C,∠ADE=∠AED,
∴∠ADC-∠EDC=∠EDC+∠C,
∴∠B+∠BAD-∠EDC=∠EDC+∠B,
得:∠CDE=∠BAD.
1
1.如图,在△ABC中,D是BC延长线上一点,∠B=40°,∠ACD=120°,则∠A等于( )
A. 60° B. 70° C. 80° D. 90°
2.将一副三角板按如图所示的方式叠放,则∠α等于( )
A. 60° B. 76° C. 100° D. 75°
3.如图,点D在线段BC的延长线上,点E为边AB上一点,延长CA到点F,连接EF,则下列结论错误的是( )
A. B.
C. D.
4.如图,已知AB∥CD,∠BAE=91°,∠DCE=120°,则∠AEC的度数是( )
A.29° B.30° C.31° D.33°
5.下列语句中,正确的是( )
A.三角形的外角大于任何一个内角
B.三角形的外角中,至少有两个钝角
C.三角形的外角等于这个三角形的两个内角之和
D.三角形的外角中,至少有一个钝角
6.如果一个三角形的两个外角之和为270°,那么这个三角形是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.无法确定
7.如图所示,在折纸活动中,将△ABC沿着DE折叠压平,A与A′重合,若∠A=60°,则∠1+∠2=( )
A.140° B.130° C.110° D.70°
8.将一副三角板按如图所示的方式放置,图中∠BAF的大小等于
A.15° B. C. D.
9.如图,若∠A=60°,∠B=48°,∠C=32°,则∠BDC=( )
A.102° B.160° C.150° D.140°
10.根据如图所示角的度数,求出其中∠α的度数.
(1)α= , (2)α= ,(3)α= .
11.已知:如图,AB∥EF,∠ABC=80°,∠CDF=140°,求的度数.
12.如图,∠ABD,∠ACD的角平分线交于点P,若∠A=55°,∠D=15°,求∠P的度数.
13.如图所示,在△ABC中,∠1=∠2,∠C>∠B,点E在AD的延长线上,且EF⊥BC于F.试探索∠DEF与∠B,∠C的大小关系;
14.如图,在△ABC中,∠B=30°,∠BAC=90°,点P是BC的动点(不与点B,C重合),AI、CI分别是∠PAC和∠PCA的角平分线,∠AIC的取值范围为m<∠AIC
(1)当∠BAD=70°,求∠CDE的度数;
(2)当点D在BC(点B、C除外)边上运动时,试写出∠BAD与∠CDE的数量关系,并说明理由.
参考答案
1.C
解:∵∠ACD=120°,∠B=40°,
∴∠A=∠ACD-∠B=120°-40°=80°.
2.D
解析:根据三角板的特点,可知∠1=45°,然后根据三角形的外角,可求∠α=75°.
3.C
解:∵,
∴,故A选项正确,不符合题意;
由三角形外角性质即可直接得出,故B选项正确,不符合题意;
没有条件可以证明出和的关系,故C选项错误,符合题意;
∵,,
∴,
∴,故D选项正确,不符合题意;
A
解:延长DC,交AE于点M,如图所示:
∴AB∥CD,
∴∠CME=∠BAE=91°,
∴∠AEC=∠DCE﹣∠CME=10°﹣91°=29°.
B
解:因为三角形的内角中最多有一个钝角,所以外角中最多有一个锐角,即外角中至少有两个钝角.
C
解:因为三角形的外角和360°,而两个外角的和为270°,所以另一个外角为90°,所以与这个外角相邻的内有为90°.
C
解:如图,连接AA',∠1=∠3+∠4,∠2=∠5+∠6,
∴∠1+∠2=∠3+∠4+∠5+∠6=∠DAE+∠DA'E=120°,
8. A
解:∵∠DAC=∠DFE+∠C=60°+45°=105°,
∴∠CAF=180°-∠DAC=75°,
∴∠BAF=90°-∠CAF=15°
9. D
解:如图,延长AD,
∵∠1=∠B+∠BAD,∠2=∠C+∠CAD,∠A=60°,∠B=48°,∠C=32°,
∴∠1+∠2=∠B+∠C+∠BAC=48°+32°+60°=140°.
10. (1)48°; (2)27°; (3)85°;
解:(1)α=120°-72°=48°;
(2)48°+ α=20°+55°,α=27°;
(3)α=40°+25°+20°=85°.
11. 40°
解:∠EDC=180°-∠CDF=180°-140°=40°,
∵AB∥EF,∠ABC=80°,
∴∠EGC=∠ABC=80°,
又∵∠EGC=∠BCD+∠EDC,
∴∠BCD=80°-40°=40°.
12. 解:延长PC交BD于E,设AC、PB交于F,
∵∠A+∠ABF+∠AFB=∠P+∠PCF+∠PFC=180°,
∵∠AFB=∠PFC,
∴∠P+∠PCF=∠A+∠ABF,
∵∠P+∠PBE=∠PED,∠PED=∠PCD﹣∠D,
∴∠P+∠PBE=∠PCD﹣∠D,
∴2∠P+∠PCF+∠PBE=∠A﹣∠D+∠ABF+∠PCD,
∵PB、PC是角平分线
∴∠PCF=∠PCD,∠ABF=∠PBE,
∴2∠P=∠A﹣∠D
∵∠A=55°,∠D=15°,
∴∠P=20°.
13. 解:∵ ∠BAC=180°-(∠B+∠C), ∠1=∠2,
∴ ∠1=∠BAC=[180°-(∠B+∠C)]=90°-(∠B+∠C).
∴ ∠EDF=∠B+∠1=∠B+90°-(∠B+∠C)=90°+(∠B-∠C).
又∵ EF⊥BC,∴ ∠EFD=90°.
∴ ∠DEF=90°-∠EDF=90°-[90°+(∠B-∠C)]=(∠C-∠B).
14. 105°,150°
解:如图:延长AI交BC于点D,
∵∠BAC=90°,∠B=30°,
∴∠PCA=60°,∠PAC<90°,
∵AI、CI分别平分∠PAC,∠PCA,
∴∠IAC=∠PAC<45°,∠BAD>45°,∠PCI=∠ICA=∠PCA=30°,
∴∠IAC=180°-∠AIC-∠ICA,
∴180°-∠AIC-∠ICA<45°,
∴∠AIC>105°,
∵∠AIC=∠IDC+∠ICP=∠BAD+∠B+∠PCI,
∠BAD>45°,
∴∠BAD=∠AIC-∠B-∠PCI>45°,
∴∠AIC>135°,
∴105°<∠AIC<150°,
∴m=105°,n=150°.
15. 解:(1)∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=70°+50°=120°,
∵∠AED是△CDE的外角,
∴∠AED=∠C+∠EDC.
∵∠B=∠C,∠ADE=∠AED,
∴∠ADC-∠EDC=∠EDC+∠C,
∴120°-∠EDC=50°+∠EDC,
解得:∠CDE=35°;
(2)∠CDE=∠BAD,
理由:∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD,
∵∠AED是△CDE的外角,
∴∠AED=∠C+∠CDE,
∵∠B=∠C,∠ADE=∠AED,
∴∠ADC-∠EDC=∠EDC+∠C,
∴∠B+∠BAD-∠EDC=∠EDC+∠B,
得:∠CDE=∠BAD.
1
