初中数学人教版八上12.1 全等三角形 习题(含答案)
文档属性
| 名称 | 初中数学人教版八上12.1 全等三角形 习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 87.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 13:42:40 | ||
图片预览

文档简介
12.1 全等三角形
1.如图,△ABC≌△ECD,AB和EC是对应边,A和E是对应点,C和D是对应顶点,则下列结论中错误的是( )
A. AB=CE B. ∠A=∠E C. ∠B=∠D D.AC=DE
2.如图,在△ABC中,点B在MN上,∠A :∠ABC :∠BCA =3:5:10,又△MNC≌△ABC,则∠BCM :∠BCN等于( )
A.1:2 B.1:4 C.2:3 D.1:3
3.下列命题中,真命题的个数是 ( )
①全等三角形的周长相等 ②全等三角形的对应角相等
③全等三角形的面积相等 ④面积相等的两个三角形全等
A.4个 B.3个 C.2个 D.1个
4.如图,△ABC≌△BAD,A和B,C和D是对应顶点,如果AB=5,BD=6,AD=4,那么BC等于( )
A.6 B.5 C.4 D.无法确定
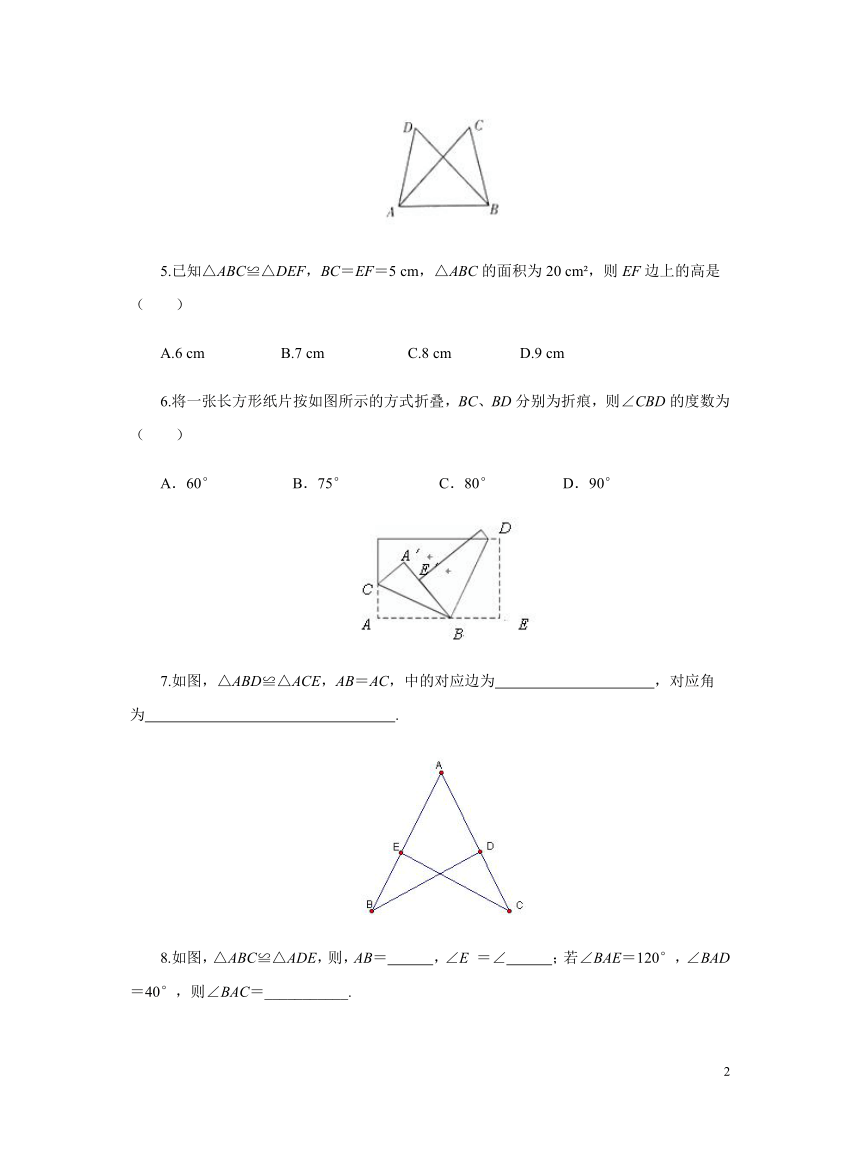
5.已知△ABC≌△DEF,BC=EF=5 cm,△ABC的面积为20 cm ,则EF边上的高是( )
A.6 cm B.7 cm C.8 cm D.9 cm
6.将一张长方形纸片按如图所示的方式折叠,BC、BD分别为折痕,则∠CBD的度数为( )
A.60° B.75° C.80° D.90°
7.如图,△ABD≌△ACE,AB=AC,中的对应边为 ,对应角为 .
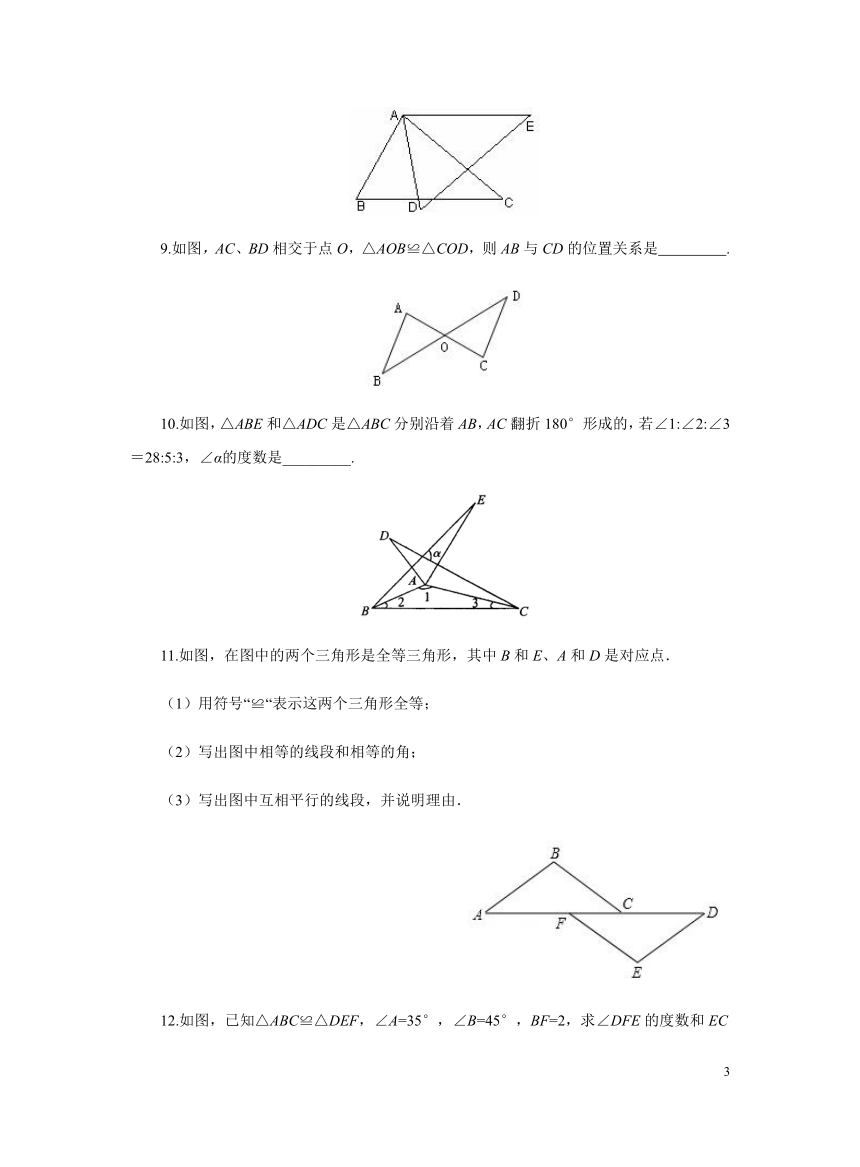
8.如图,△ABC≌△ADE,则,AB= ,∠E =∠ ;若∠BAE=120°,∠BAD=40°,则∠BAC=___________.
9.如图,AC、BD相交于点O,△AOB≌△COD,则AB与CD的位置关系是 .
10.如图,△ABE和△ADC是△ABC分别沿着AB,AC翻折180°形成的,若∠1:∠2:∠3=28:5:3,∠α的度数是_________.
11.如图,在图中的两个三角形是全等三角形,其中B和E、A和D是对应点.
(1)用符号“≌“表示这两个三角形全等;
(2)写出图中相等的线段和相等的角;
(3)写出图中互相平行的线段,并说明理由.
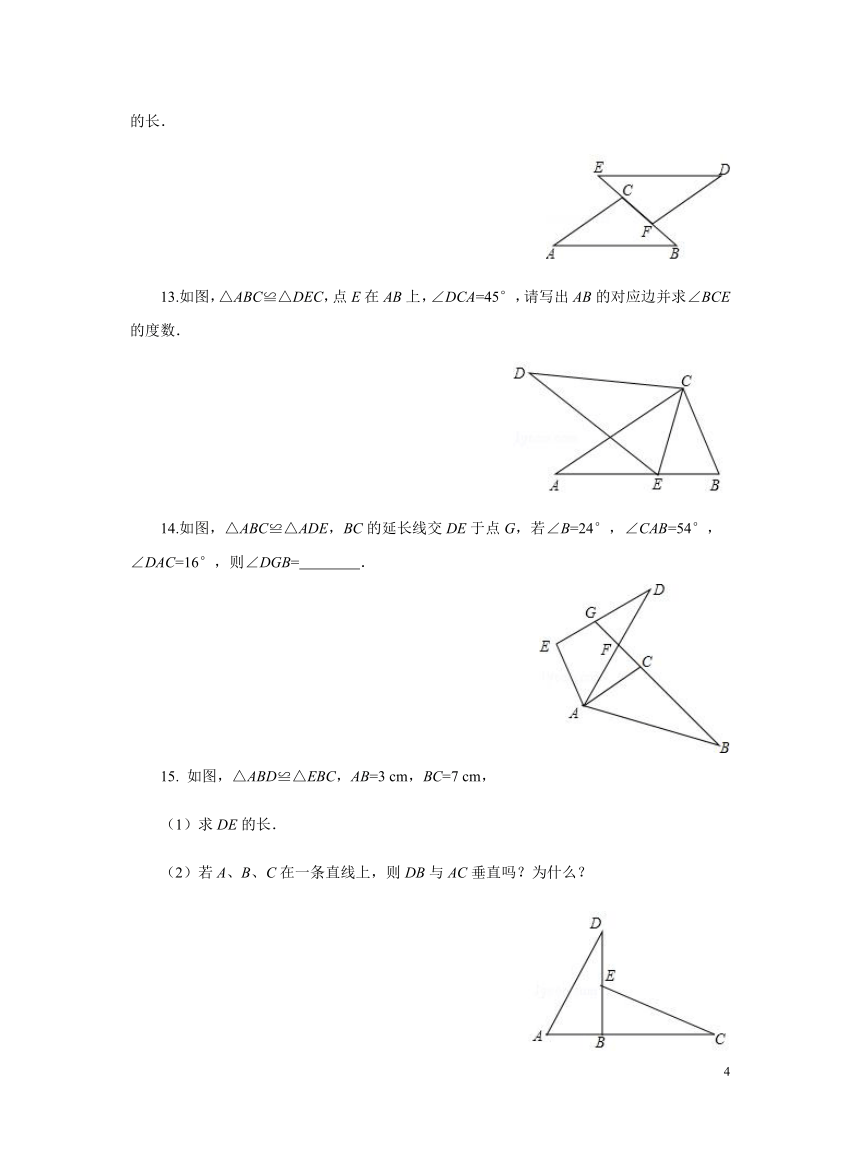
12.如图,已知△ABC≌△DEF,∠A=35°,∠B=45°,BF=2,求∠DFE的度数和EC的长.
13.如图,△ABC≌△DEC,点E在AB上,∠DCA=45°,请写出AB的对应边并求∠BCE的度数.
14.如图,△ABC≌△ADE,BC的延长线交DE于点G,若∠B=24°,∠CAB=54°,∠DAC=16°,则∠DGB= .
15. 如图,△ABD≌△EBC,AB=3 cm,BC=7 cm,
(1)求DE的长.
(2)若A、B、C在一条直线上,则DB与AC垂直吗?为什么?
参考答案
1.C
解析:∵C和D是对应顶点,∴∠ACD=∠D,∠B≠∠D
2.B
解析:设∠A=3x,∠ABC=5x,∠BCA=10x,
则3x+5x+10x=18x=180°,x=10°.
又∵△MNC≌△ABC,
∴∠N=∠ABC=50°,∠ACB=∠MCN=100°,CN=CB,
∴∠N=∠CBN=50°,∠BCN=180°-50°-50°=80°,
∴∠BCM:∠BCN=20°:80°=1:4.
3.B
解析:根据全等三角形的性质可以确定①②③是正确的.
4.C
解析:依据全等三角形的性质,∵△ABC≌△BAD,∴BC=AD=4.
5.C
解析:∵△ABC≌△DEF,∴S△ABC=S△DEF=20 cm ,EF边上的高= cm.
6.D
解析:折叠得到的新图形与原图形全等,其中的对应角相等,∴∠CBD=180°÷2=90°.
7.AB和AC,AD和AE,BD和CE,∠A和∠A,∠B和∠C,∠ADB和∠AEC.
解析:根据全等三角形的性质确定对应边和对应角.
8.AD; C; 80°
解析:∠BAC=∠DAE=∠BAE-∠BAD=120°-40°=80°;
9.平行;
解析:∵△AOB≌△COD,∴∠B=∠D,∴AB∥CD.
10.∠α=80°
解:∵∠1∶∠2∶∠3=28∶5∶3,设∠1=28x,∠2=5x,∠3=3x,
∴28x+5x+3x=36x=180°,x=5°
即∠1=140°,∠2=25°,∠3=15°
∵△ABE和△ADC是△ABC分别沿着AB,AC翻折180°形成的,
∴△ABE≌△ADC≌△ABC
∴∠2=∠ABE,∠3=∠ACD
∴∠α=∠EBC+∠BCD=2∠2+2∠3=50°+30°=80°
11.解:(1)△ABC≌△DEF;
(2)AB=DE,BC=EF,AC=DF;∠A=∠D,∠B=∠E,∠ACB=∠DFE;
(3)BC∥EF,AB∥DE,
理由如下:
∵△ABC≌△DEF,
∴∠A=∠D,∠ACB=∠DFE,
∴AB∥DE,BC∥EF.
12.解:∵∠A=35°,∠B=45°,
∴∠ACB=180°-∠A-∠B=180°-35°-45°=100°,
∵△ABC≌△DEF,
∴∠DFE=∠ACB=100°,EF=BC,
∴EF-CF=BC-CF,即EC=BF,
∴EC=BF=2.
13.解:AB的对应边为DE,
∵△ABC≌△DEC,
∴∠ACB=∠DCE,
∴∠ACB—∠ACE=∠DCE—∠ACE,
即∠BCE=∠DCA=45°.
14.解:∵∠B=24°,∠CAB=54°,∠DAC=16°,
∴∠AFB=180°-(∠B+∠CAB+∠DAC)=86°,
∴∠GFD=∠AFB=86°,
∵△ABC≌△ADE,∠B=24°,
∴∠D=∠B=24°,
∴∠DGB=180°-∠D-∠DFG=70°.
15.解:(1)∵△ABD≌△EBC,
∴BD=BC=7 cm,BE=AB=3 cm,
∴DE=BD-BE=4 cm;
(2)DB⊥AC.理由如下:
∵△ABD≌△EBC,
∴∠ABD=∠EBC,
又∵∠ABD+∠EBC=180°,
∴∠ABD=∠EBC=90°,
∴DB⊥AC.
1
1.如图,△ABC≌△ECD,AB和EC是对应边,A和E是对应点,C和D是对应顶点,则下列结论中错误的是( )
A. AB=CE B. ∠A=∠E C. ∠B=∠D D.AC=DE
2.如图,在△ABC中,点B在MN上,∠A :∠ABC :∠BCA =3:5:10,又△MNC≌△ABC,则∠BCM :∠BCN等于( )
A.1:2 B.1:4 C.2:3 D.1:3
3.下列命题中,真命题的个数是 ( )
①全等三角形的周长相等 ②全等三角形的对应角相等
③全等三角形的面积相等 ④面积相等的两个三角形全等
A.4个 B.3个 C.2个 D.1个
4.如图,△ABC≌△BAD,A和B,C和D是对应顶点,如果AB=5,BD=6,AD=4,那么BC等于( )
A.6 B.5 C.4 D.无法确定
5.已知△ABC≌△DEF,BC=EF=5 cm,△ABC的面积为20 cm ,则EF边上的高是( )
A.6 cm B.7 cm C.8 cm D.9 cm
6.将一张长方形纸片按如图所示的方式折叠,BC、BD分别为折痕,则∠CBD的度数为( )
A.60° B.75° C.80° D.90°
7.如图,△ABD≌△ACE,AB=AC,中的对应边为 ,对应角为 .
8.如图,△ABC≌△ADE,则,AB= ,∠E =∠ ;若∠BAE=120°,∠BAD=40°,则∠BAC=___________.
9.如图,AC、BD相交于点O,△AOB≌△COD,则AB与CD的位置关系是 .
10.如图,△ABE和△ADC是△ABC分别沿着AB,AC翻折180°形成的,若∠1:∠2:∠3=28:5:3,∠α的度数是_________.
11.如图,在图中的两个三角形是全等三角形,其中B和E、A和D是对应点.
(1)用符号“≌“表示这两个三角形全等;
(2)写出图中相等的线段和相等的角;
(3)写出图中互相平行的线段,并说明理由.
12.如图,已知△ABC≌△DEF,∠A=35°,∠B=45°,BF=2,求∠DFE的度数和EC的长.
13.如图,△ABC≌△DEC,点E在AB上,∠DCA=45°,请写出AB的对应边并求∠BCE的度数.
14.如图,△ABC≌△ADE,BC的延长线交DE于点G,若∠B=24°,∠CAB=54°,∠DAC=16°,则∠DGB= .
15. 如图,△ABD≌△EBC,AB=3 cm,BC=7 cm,
(1)求DE的长.
(2)若A、B、C在一条直线上,则DB与AC垂直吗?为什么?
参考答案
1.C
解析:∵C和D是对应顶点,∴∠ACD=∠D,∠B≠∠D
2.B
解析:设∠A=3x,∠ABC=5x,∠BCA=10x,
则3x+5x+10x=18x=180°,x=10°.
又∵△MNC≌△ABC,
∴∠N=∠ABC=50°,∠ACB=∠MCN=100°,CN=CB,
∴∠N=∠CBN=50°,∠BCN=180°-50°-50°=80°,
∴∠BCM:∠BCN=20°:80°=1:4.
3.B
解析:根据全等三角形的性质可以确定①②③是正确的.
4.C
解析:依据全等三角形的性质,∵△ABC≌△BAD,∴BC=AD=4.
5.C
解析:∵△ABC≌△DEF,∴S△ABC=S△DEF=20 cm ,EF边上的高= cm.
6.D
解析:折叠得到的新图形与原图形全等,其中的对应角相等,∴∠CBD=180°÷2=90°.
7.AB和AC,AD和AE,BD和CE,∠A和∠A,∠B和∠C,∠ADB和∠AEC.
解析:根据全等三角形的性质确定对应边和对应角.
8.AD; C; 80°
解析:∠BAC=∠DAE=∠BAE-∠BAD=120°-40°=80°;
9.平行;
解析:∵△AOB≌△COD,∴∠B=∠D,∴AB∥CD.
10.∠α=80°
解:∵∠1∶∠2∶∠3=28∶5∶3,设∠1=28x,∠2=5x,∠3=3x,
∴28x+5x+3x=36x=180°,x=5°
即∠1=140°,∠2=25°,∠3=15°
∵△ABE和△ADC是△ABC分别沿着AB,AC翻折180°形成的,
∴△ABE≌△ADC≌△ABC
∴∠2=∠ABE,∠3=∠ACD
∴∠α=∠EBC+∠BCD=2∠2+2∠3=50°+30°=80°
11.解:(1)△ABC≌△DEF;
(2)AB=DE,BC=EF,AC=DF;∠A=∠D,∠B=∠E,∠ACB=∠DFE;
(3)BC∥EF,AB∥DE,
理由如下:
∵△ABC≌△DEF,
∴∠A=∠D,∠ACB=∠DFE,
∴AB∥DE,BC∥EF.
12.解:∵∠A=35°,∠B=45°,
∴∠ACB=180°-∠A-∠B=180°-35°-45°=100°,
∵△ABC≌△DEF,
∴∠DFE=∠ACB=100°,EF=BC,
∴EF-CF=BC-CF,即EC=BF,
∴EC=BF=2.
13.解:AB的对应边为DE,
∵△ABC≌△DEC,
∴∠ACB=∠DCE,
∴∠ACB—∠ACE=∠DCE—∠ACE,
即∠BCE=∠DCA=45°.
14.解:∵∠B=24°,∠CAB=54°,∠DAC=16°,
∴∠AFB=180°-(∠B+∠CAB+∠DAC)=86°,
∴∠GFD=∠AFB=86°,
∵△ABC≌△ADE,∠B=24°,
∴∠D=∠B=24°,
∴∠DGB=180°-∠D-∠DFG=70°.
15.解:(1)∵△ABD≌△EBC,
∴BD=BC=7 cm,BE=AB=3 cm,
∴DE=BD-BE=4 cm;
(2)DB⊥AC.理由如下:
∵△ABD≌△EBC,
∴∠ABD=∠EBC,
又∵∠ABD+∠EBC=180°,
∴∠ABD=∠EBC=90°,
∴DB⊥AC.
1
