初中数学人教版八上12.2全等三角形的判定第1课时 教案
文档属性
| 名称 | 初中数学人教版八上12.2全等三角形的判定第1课时 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 102.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 13:48:01 | ||
图片预览

文档简介
12.2 全等三角形的判定第1课时
【教学目标】
1.知识与技能:掌握三角形全等的“边边边”条件.
2.过程与方法:经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
3.情感态度与价值观:通过对问题的共同探讨,培养学生的协作精神.
【教学重难点】
重点:对基本事实“边边边”的理解及运用.
难点:构建三角形全等条件的探索思路及尺规作图.
【教学方法】
作图实验操作、小组协作法.
【教学过程】
新课导入:
创设情境,提出问题:
1. 什么叫全等三角形?
2. 全等三角形有什么性质?
3.已知△ABC ≌△DEF,找出其中相等的边与角.
1.能够重合的两个三角形叫全等三角形.
2.全等三角形的对应边相等,对应角相等.
3.①AB=DE,②BC=EF,③ CA=FD,④∠A=∠D,⑤∠B=∠E,⑥∠C=∠F.
新课讲授:
(一)判定全等三角形的思路
△ABC与△A′B′C′全等是不是一定要满足上述六个条件呢?满足上述六个条件中的一部分是否也可以保证△ABC≌△A′B′C′呢?
如果两个三角形满足上述六个条件中的一个可以判定两个三角形全等吗?
(1)一条边相等.
(2)一个角相等.
动画演示一边、一角对应相等时的三角形是否重合.
归纳结论:
有一个条件相等不能保证两个三角形全等.
两个条件可以吗?
(1)有两个角;(2)有两条边;(3)有一个角和一条边;
动画演示两边、两角或一边与一角对应相等时的三角形是否重合.
归纳结论:
有两个条件对应相等不能保证三角形全等.
三个条件可以吗?
(1)有三个角;(2)有三条边
动画演示三个角对应相等时的三角形是否重合.
归纳结论:
三个内角对应相等的三角形不一定全等.
实践探究:
先任意画一个△ABC,再画一个△A′B′C′ ,使A′B ′ =AB,B′C ′ =BC,C′A ′ =CA.把画好的三角形△A′B′C′剪下来,放到△ABC上,它们全等吗?
学生分组探究图形的画法.展示所画三角形.
画法: (1)画线段B′C′=BC ;
(2)分别以B′,C′为圆心,线段AB,AC 的长度为半径画弧,两弧交于点A′;
(3)连接线段A′B′,A′C′.
归纳结论:
三条边分别相等的两个三角形全等.
(二)“边边边”定理
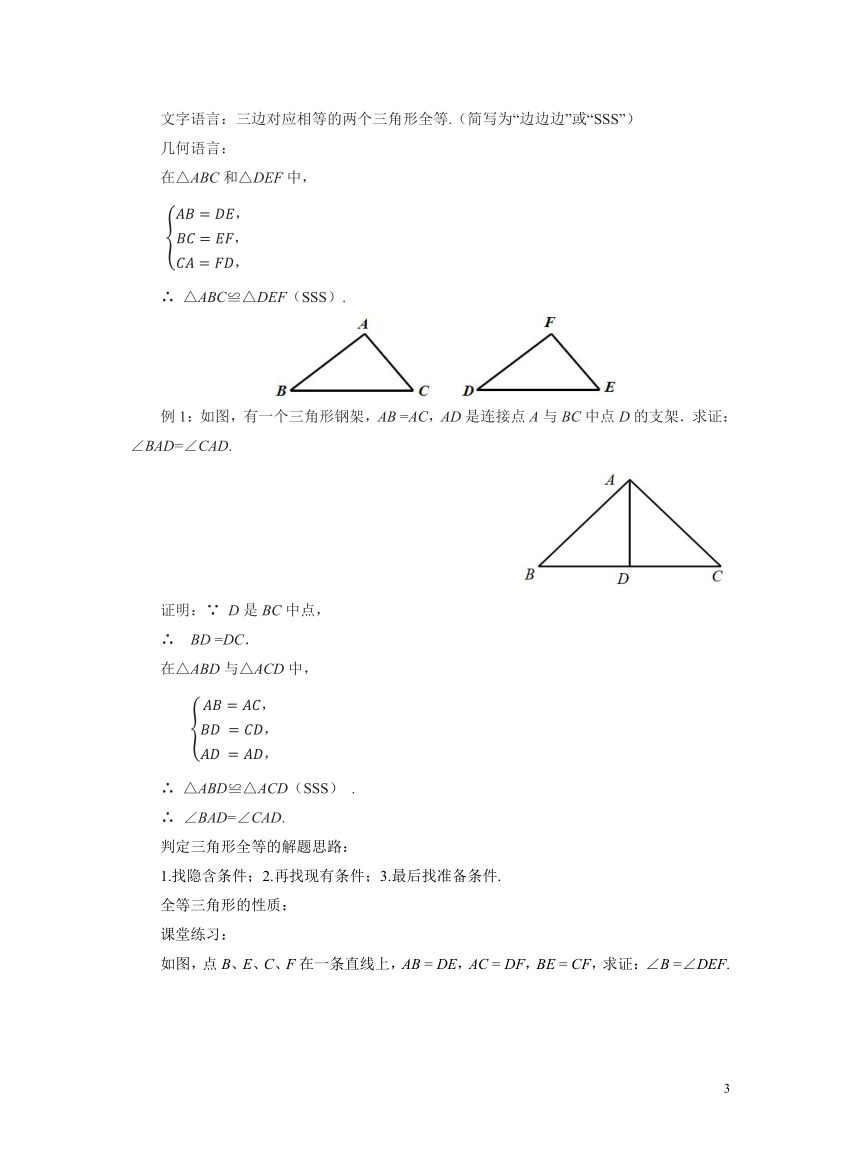
文字语言:三边对应相等的两个三角形全等.(简写为“边边边”或“SSS”)
几何语言:
在△ABC和△DEF中,
∴ △ABC≌△DEF(SSS).
例1:如图,有一个三角形钢架,AB =AC,AD是连接点A与BC中点D的支架.求证:∠BAD=∠CAD.
证明:∵ D是BC中点,
∴ BD =DC.
在△ABD与△ACD中,
∴ △ABD≌△ACD(SSS) .
∴ ∠BAD=∠CAD.
判定三角形全等的解题思路:
1.找隐含条件;2.再找现有条件;3.最后找准备条件.
全等三角形的性质:
课堂练习:
如图,点B、E、C、F在一条直线上,AB = DE,AC = DF,BE = CF,求证:∠B =∠DEF.
证明:∵BE = CF,
∴BE+EC = CF+EC,即BC = EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).
∴∠B =∠DEF.
动手实践:
用尺规作一个角等于已知角.
已知:∠AOB.求作:∠A′O′B′=∠AOB.
作法:
(1)以点O为圆心,任意长为半径画弧,分别交OA,
OB 于点C、D;
(2)画一条射线O′A′,以点O′为圆心,OC 长为半
径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD 长为半径画弧,与第2 步中
所画的弧交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB.
思考探讨:作图的理论依据是什么?(“边边边”定理)
引导学生认识为什么这样作图能够得到∠A′O′B′=∠AOB.从而得出结论.
课堂练习:
1.已知∠AOB,点C是OB边上的一点,用尺规作图,画出经过点C与OA平行的直线.
解:如图所示:
作法:(1)以点O为圆心,任意长为半径画弧,分别交OA,OB于点D,E;
(2)以点C为圆心,OD长为半径画弧,交OB于点F;
(3)以点F为圆心,DE长为半径画弧,与第2步中所画的弧相交于点P ;
(4)过C,P两点作直线,直线CP即为要求作的直线.
2.如图,AD=BC,AC=BD.求证:∠ABD=∠BAC .
证明:连结AB两点,
在△ABD和△BAC中,
∴△ABD≌△BAC(SSS).
∠ABD=∠BAC.
3.如图,点B、E、C、F在一条直线上,AB = DE,AC = DF,BE = CF,求证:∠A =∠D.
证明:∵BE = CF,
∴BE+EC = CF+EC,即BC = EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).
∴∠A =∠D.
课堂小结:
说一说本节课都有哪些收获.
1.了解两个基本事实;三边分别相等的两个三角形全等.
2.确定三角形全等的基本思路:
(1)说明两三角形全等所需的条件应按对应边的顺序书写.
(2)结论中所出现的边必须在所证明的两个三角形中.
(3)已知两边,必须找“夹角”或第三边.
(4)已知一角和这角的一夹边,必须找这角的另一夹边.
作业布置:
1.尺规作图:已知△ABC,再画出一个△A′B′C′ ,使A′B′= AB,B′C′ =BC,A′ C′ =AC.写出△ABC≌△A′B′C′的依据.
2.收集用“SSS”定理证明全等的习题两道,体会证明三角形全等的几何推理思路,熟练掌握证明的步骤.
3.本节配套习题.
【板书设计】
“边边边”定理.
注意:
1. 说明两三角形全等所需的条件应按对应边的顺序书写.
2. 结论中所出现的边必须在所证明的两个三角形中.
【课后反思】
本节课从操作探究活动入手,有效地激发了学生的学习积极性和探究热情,提高了课堂的教学效率,促进了学生对新知识的理解和掌握. 从课堂教学的情况来看,学生对“边边边”掌握较好,达到了教学的预期目的.存在的问题是少数学生在辅助线的构造上感到困难,不知道如何添加合理的辅助线,还需要在今后的教学中进一步加强巩固和训练.
1
【教学目标】
1.知识与技能:掌握三角形全等的“边边边”条件.
2.过程与方法:经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
3.情感态度与价值观:通过对问题的共同探讨,培养学生的协作精神.
【教学重难点】
重点:对基本事实“边边边”的理解及运用.
难点:构建三角形全等条件的探索思路及尺规作图.
【教学方法】
作图实验操作、小组协作法.
【教学过程】
新课导入:
创设情境,提出问题:
1. 什么叫全等三角形?
2. 全等三角形有什么性质?
3.已知△ABC ≌△DEF,找出其中相等的边与角.
1.能够重合的两个三角形叫全等三角形.
2.全等三角形的对应边相等,对应角相等.
3.①AB=DE,②BC=EF,③ CA=FD,④∠A=∠D,⑤∠B=∠E,⑥∠C=∠F.
新课讲授:
(一)判定全等三角形的思路
△ABC与△A′B′C′全等是不是一定要满足上述六个条件呢?满足上述六个条件中的一部分是否也可以保证△ABC≌△A′B′C′呢?
如果两个三角形满足上述六个条件中的一个可以判定两个三角形全等吗?
(1)一条边相等.
(2)一个角相等.
动画演示一边、一角对应相等时的三角形是否重合.
归纳结论:
有一个条件相等不能保证两个三角形全等.
两个条件可以吗?
(1)有两个角;(2)有两条边;(3)有一个角和一条边;
动画演示两边、两角或一边与一角对应相等时的三角形是否重合.
归纳结论:
有两个条件对应相等不能保证三角形全等.
三个条件可以吗?
(1)有三个角;(2)有三条边
动画演示三个角对应相等时的三角形是否重合.
归纳结论:
三个内角对应相等的三角形不一定全等.
实践探究:
先任意画一个△ABC,再画一个△A′B′C′ ,使A′B ′ =AB,B′C ′ =BC,C′A ′ =CA.把画好的三角形△A′B′C′剪下来,放到△ABC上,它们全等吗?
学生分组探究图形的画法.展示所画三角形.
画法: (1)画线段B′C′=BC ;
(2)分别以B′,C′为圆心,线段AB,AC 的长度为半径画弧,两弧交于点A′;
(3)连接线段A′B′,A′C′.
归纳结论:
三条边分别相等的两个三角形全等.
(二)“边边边”定理
文字语言:三边对应相等的两个三角形全等.(简写为“边边边”或“SSS”)
几何语言:
在△ABC和△DEF中,
∴ △ABC≌△DEF(SSS).
例1:如图,有一个三角形钢架,AB =AC,AD是连接点A与BC中点D的支架.求证:∠BAD=∠CAD.
证明:∵ D是BC中点,
∴ BD =DC.
在△ABD与△ACD中,
∴ △ABD≌△ACD(SSS) .
∴ ∠BAD=∠CAD.
判定三角形全等的解题思路:
1.找隐含条件;2.再找现有条件;3.最后找准备条件.
全等三角形的性质:
课堂练习:
如图,点B、E、C、F在一条直线上,AB = DE,AC = DF,BE = CF,求证:∠B =∠DEF.
证明:∵BE = CF,
∴BE+EC = CF+EC,即BC = EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).
∴∠B =∠DEF.
动手实践:
用尺规作一个角等于已知角.
已知:∠AOB.求作:∠A′O′B′=∠AOB.
作法:
(1)以点O为圆心,任意长为半径画弧,分别交OA,
OB 于点C、D;
(2)画一条射线O′A′,以点O′为圆心,OC 长为半
径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD 长为半径画弧,与第2 步中
所画的弧交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB.
思考探讨:作图的理论依据是什么?(“边边边”定理)
引导学生认识为什么这样作图能够得到∠A′O′B′=∠AOB.从而得出结论.
课堂练习:
1.已知∠AOB,点C是OB边上的一点,用尺规作图,画出经过点C与OA平行的直线.
解:如图所示:
作法:(1)以点O为圆心,任意长为半径画弧,分别交OA,OB于点D,E;
(2)以点C为圆心,OD长为半径画弧,交OB于点F;
(3)以点F为圆心,DE长为半径画弧,与第2步中所画的弧相交于点P ;
(4)过C,P两点作直线,直线CP即为要求作的直线.
2.如图,AD=BC,AC=BD.求证:∠ABD=∠BAC .
证明:连结AB两点,
在△ABD和△BAC中,
∴△ABD≌△BAC(SSS).
∠ABD=∠BAC.
3.如图,点B、E、C、F在一条直线上,AB = DE,AC = DF,BE = CF,求证:∠A =∠D.
证明:∵BE = CF,
∴BE+EC = CF+EC,即BC = EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).
∴∠A =∠D.
课堂小结:
说一说本节课都有哪些收获.
1.了解两个基本事实;三边分别相等的两个三角形全等.
2.确定三角形全等的基本思路:
(1)说明两三角形全等所需的条件应按对应边的顺序书写.
(2)结论中所出现的边必须在所证明的两个三角形中.
(3)已知两边,必须找“夹角”或第三边.
(4)已知一角和这角的一夹边,必须找这角的另一夹边.
作业布置:
1.尺规作图:已知△ABC,再画出一个△A′B′C′ ,使A′B′= AB,B′C′ =BC,A′ C′ =AC.写出△ABC≌△A′B′C′的依据.
2.收集用“SSS”定理证明全等的习题两道,体会证明三角形全等的几何推理思路,熟练掌握证明的步骤.
3.本节配套习题.
【板书设计】
“边边边”定理.
注意:
1. 说明两三角形全等所需的条件应按对应边的顺序书写.
2. 结论中所出现的边必须在所证明的两个三角形中.
【课后反思】
本节课从操作探究活动入手,有效地激发了学生的学习积极性和探究热情,提高了课堂的教学效率,促进了学生对新知识的理解和掌握. 从课堂教学的情况来看,学生对“边边边”掌握较好,达到了教学的预期目的.存在的问题是少数学生在辅助线的构造上感到困难,不知道如何添加合理的辅助线,还需要在今后的教学中进一步加强巩固和训练.
1
