初中数学人教版八上12.2全等三角形的判定(第3课时) 教案
文档属性
| 名称 | 初中数学人教版八上12.2全等三角形的判定(第3课时) 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 106.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 00:00:00 | ||
图片预览


文档简介
12.2 全等三角形的判定第3课时
【教学目标】
1.知识与技能:掌握已知三角形两个内角和一条边的长度怎么画三角形;掌握三角形全等的证明方法:“角边角”和“角角边”;能熟练运用其进行证明.
2.过程与方法:学生经历探索三角形全等条件的过程,体会如何探索研究问题,让学生通过探究,体会分类讨论的思想.
3.情感态度与价值观:通过探究全等三角形的证明方法,体会分类讨论的思想,有助于学生形成严谨的学习习惯以及形成较强的逻辑推理能力.
【教学重难点】
重点:对基本事实“角边角”和“角角边”的理解及运用.
难点:运用“角边角”和“角角边”证明三角形从而推理出图形的边、角关系.
【教学方法】
作图操作、合情推理法.
【教学过程】
新课导入:
创设情境,提出问题:
说出基本事实“SSS”和“SAS”的内容以及进行三角形全等判定的注意事项.
有三边对应相等的两个三角形全等(简写成 “SSS”)
2. 有两边及夹角对应相等的两个三角形全等(简写成 “SAS”)
3. 注意:
(1)说明两三角形全等所需的条件应按对应边的顺序书写.
(2)结论中所出现的边必须在所证明的两个三角形中.
(3)已知两边,必须找“夹角”或第三边.
(4)已知一角和这角的一夹边,必须找这角的另一夹边.
问题: 当三角形的六个元素已知三个元素时除了“SSS”,“SAS”外,还有其他情况吗?
三角 ×
三边 √
两边一角 √
两角一边 ?
新课讲授:
(一)“ASA”定理
教材探究4:
先任意画出一个△ABC.再画一个△A′B′C′,使A′B′=AB,∠A′=∠A,∠B′=∠B(即两角和它们的夹边分别相等).把画好的△A′B′C′剪下来,放到△ABC上,它们全等吗?
作法:
(1)画A'B'=AB;
(2)在A'B'的同旁画∠DA'B'=∠A,∠EB'A'=∠B,A'D,B'E相交于点C'.
发现:这两个三角形全等.
归纳结论:
文字语言:两角和它们的夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”).
几何语言:
在△ABC和△A′ B′ C′中,,∴ △ABC≌△ ABC(ASA).
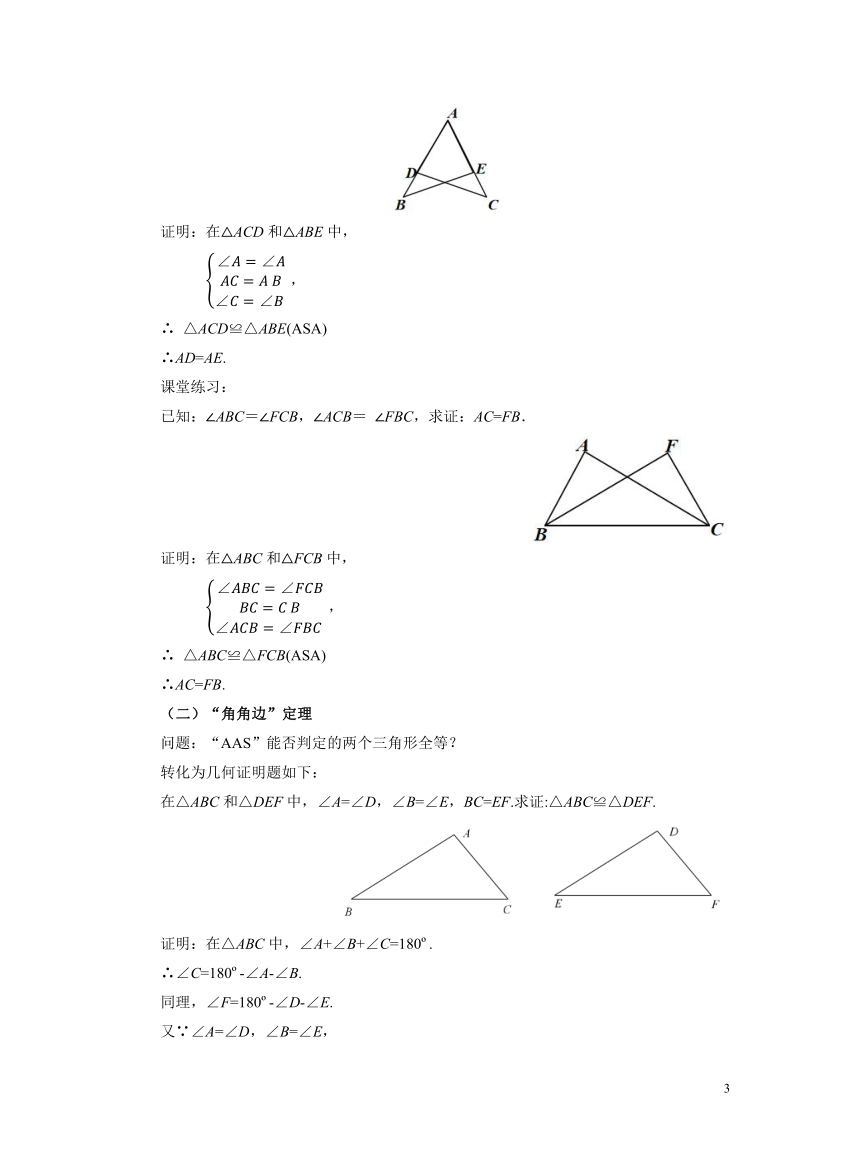
例1:如图,点D在AB上,点E在AC上,AB=AC, ∠B=∠C,求证:AD=AE.
证明:在△ACD和△ABE中,
,
∴ △ACD≌△ABE(ASA)
∴AD=AE.
课堂练习:
已知:∠ABC=∠FCB,∠ACB= ∠FBC,求证:AC=FB.
证明:在△ABC和△FCB中,
,
∴ △ABC≌△FCB(ASA)
∴AC=FB.
“角角边”定理
问题:“AAS”能否判定的两个三角形全等?
转化为几何证明题如下:
在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.求证:△ABC≌△DEF.
证明:在△ABC中,∠A+∠B+∠C=180 .
∴∠C=180 -∠A-∠B.
同理,∠F=180 -∠D-∠E.
又∵∠A=∠D,∠B=∠E,
∴∠C=∠F.
在△ABC和△DEF中,,
∴△ABC≌△DEF (ASA).
归纳结论:
两角分别相等且其中一组等角的对边相等的两个三角形全等.
简写成“角角边”或“AAS”.
几何语言:
在△ABC和△A′B′C′中,,
∴ △ABC≌△ A′ B′ C′ (AAS).
例2:如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,E.求证:DE=BD+CE.
证明:∵BD⊥m,CE⊥m,
∴∠ADB=∠CEA=90°,
∴∠ABD+∠BAD=90°.
∵AB⊥AC,
∴∠BAD+∠CAE=90°,
∠ABD=∠CAE.
在△BDA和△AEC中,,
∴△BDA≌△AEC(AAS).
∴BD=AE,AD=CE,
∴DE=DA+AE=BD+CE.
方法总结:
利用全等三角形可以解决线段之间的关系,比如线段的相等关系、和差关系等,解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化.
例3:已知:如图,△ABC ≌△A′B′C′ ,AD、A′ D′ 分别是△ABC 和△A′B′C′的高.试说明AD= A′D′ ,并用一句话说出你的发现.
解:∵△ABC ≌△A′B′C′ ,
∴AB=A'B',∠ABD=∠A'B'D'.
∵AD⊥BC,A'D'⊥B'C',
∴∠ADB=∠A'D'B'.
在△ABD和△A'B'D'中,,
∴△ABD≌△A'B'D' (AAS).
∴AD=A'D'.
引导学生归纳结论:
全等三角形对应边上的高也相等.
课堂练习:
1.△ABC和△DEF中,AB=DE,∠B=∠E,要使△ABC≌△DEF,则下列补充的条件中错误的是( )
A.AC=DF B.BC=EF C.∠A=∠D D.∠C=∠F
答案:A
2.如图∠ACB=∠DFE,BF=CE,那么应补充一个条件 ,才能使△ABC≌△DEF (写出一个即可).
答案:AB∥DE,或∠B=∠E,或∠A=∠D,或 AC=DF.
3.如图,要测量河两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A,C,E在一条直线上,这时测得DE的长就是AB的长,为什么?
证明:在△ABC和△EDC中,
∠B=∠EDC=90°,
BC=DC,
∠ACB=∠ECD.
∴△ABC≌△EDC.∴DE=AB.
4.如图,小明不慎将一块三角形模具打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适 你能说明其中理由吗
答:带1去,因为有两角且夹边相等的两个三角形全等.
课堂小结:
说一说本节课都有哪些收获.
1.了解两个基本事实;有两角及夹边对应相等的两个三角形全等(简写成 “ASA”);两角和其中一角的对边对应相等的两个三角形全等.
2.运用“ASA”“AAS”证明线段和角相等的新的方法.
作业布置:
小组探讨证明全等三角形对应边上的中线,对应角的角平分线相等.
【板书设计】
基本事实:
有两角及夹边对应相等的两个三角形全等(简写成 “ASA”);两角和其中一角的对边对应相等的两个三角形全等.
应用:
证明线段和角相等提供了新的证法;
注意:
“角角边”与“角边角”的区别.
【课后反思】
先给学生独立思考的时间,培养学生独立探究,合作学习的能力.注重让学生用自己的语言归纳和表达发现的规律,指引学生对知识与方法进行回顾总结,形成良好的反思习惯.
1
【教学目标】
1.知识与技能:掌握已知三角形两个内角和一条边的长度怎么画三角形;掌握三角形全等的证明方法:“角边角”和“角角边”;能熟练运用其进行证明.
2.过程与方法:学生经历探索三角形全等条件的过程,体会如何探索研究问题,让学生通过探究,体会分类讨论的思想.
3.情感态度与价值观:通过探究全等三角形的证明方法,体会分类讨论的思想,有助于学生形成严谨的学习习惯以及形成较强的逻辑推理能力.
【教学重难点】
重点:对基本事实“角边角”和“角角边”的理解及运用.
难点:运用“角边角”和“角角边”证明三角形从而推理出图形的边、角关系.
【教学方法】
作图操作、合情推理法.
【教学过程】
新课导入:
创设情境,提出问题:
说出基本事实“SSS”和“SAS”的内容以及进行三角形全等判定的注意事项.
有三边对应相等的两个三角形全等(简写成 “SSS”)
2. 有两边及夹角对应相等的两个三角形全等(简写成 “SAS”)
3. 注意:
(1)说明两三角形全等所需的条件应按对应边的顺序书写.
(2)结论中所出现的边必须在所证明的两个三角形中.
(3)已知两边,必须找“夹角”或第三边.
(4)已知一角和这角的一夹边,必须找这角的另一夹边.
问题: 当三角形的六个元素已知三个元素时除了“SSS”,“SAS”外,还有其他情况吗?
三角 ×
三边 √
两边一角 √
两角一边 ?
新课讲授:
(一)“ASA”定理
教材探究4:
先任意画出一个△ABC.再画一个△A′B′C′,使A′B′=AB,∠A′=∠A,∠B′=∠B(即两角和它们的夹边分别相等).把画好的△A′B′C′剪下来,放到△ABC上,它们全等吗?
作法:
(1)画A'B'=AB;
(2)在A'B'的同旁画∠DA'B'=∠A,∠EB'A'=∠B,A'D,B'E相交于点C'.
发现:这两个三角形全等.
归纳结论:
文字语言:两角和它们的夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”).
几何语言:
在△ABC和△A′ B′ C′中,,∴ △ABC≌△ ABC(ASA).
例1:如图,点D在AB上,点E在AC上,AB=AC, ∠B=∠C,求证:AD=AE.
证明:在△ACD和△ABE中,
,
∴ △ACD≌△ABE(ASA)
∴AD=AE.
课堂练习:
已知:∠ABC=∠FCB,∠ACB= ∠FBC,求证:AC=FB.
证明:在△ABC和△FCB中,
,
∴ △ABC≌△FCB(ASA)
∴AC=FB.
“角角边”定理
问题:“AAS”能否判定的两个三角形全等?
转化为几何证明题如下:
在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.求证:△ABC≌△DEF.
证明:在△ABC中,∠A+∠B+∠C=180 .
∴∠C=180 -∠A-∠B.
同理,∠F=180 -∠D-∠E.
又∵∠A=∠D,∠B=∠E,
∴∠C=∠F.
在△ABC和△DEF中,,
∴△ABC≌△DEF (ASA).
归纳结论:
两角分别相等且其中一组等角的对边相等的两个三角形全等.
简写成“角角边”或“AAS”.
几何语言:
在△ABC和△A′B′C′中,,
∴ △ABC≌△ A′ B′ C′ (AAS).
例2:如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,E.求证:DE=BD+CE.
证明:∵BD⊥m,CE⊥m,
∴∠ADB=∠CEA=90°,
∴∠ABD+∠BAD=90°.
∵AB⊥AC,
∴∠BAD+∠CAE=90°,
∠ABD=∠CAE.
在△BDA和△AEC中,,
∴△BDA≌△AEC(AAS).
∴BD=AE,AD=CE,
∴DE=DA+AE=BD+CE.
方法总结:
利用全等三角形可以解决线段之间的关系,比如线段的相等关系、和差关系等,解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化.
例3:已知:如图,△ABC ≌△A′B′C′ ,AD、A′ D′ 分别是△ABC 和△A′B′C′的高.试说明AD= A′D′ ,并用一句话说出你的发现.
解:∵△ABC ≌△A′B′C′ ,
∴AB=A'B',∠ABD=∠A'B'D'.
∵AD⊥BC,A'D'⊥B'C',
∴∠ADB=∠A'D'B'.
在△ABD和△A'B'D'中,,
∴△ABD≌△A'B'D' (AAS).
∴AD=A'D'.
引导学生归纳结论:
全等三角形对应边上的高也相等.
课堂练习:
1.△ABC和△DEF中,AB=DE,∠B=∠E,要使△ABC≌△DEF,则下列补充的条件中错误的是( )
A.AC=DF B.BC=EF C.∠A=∠D D.∠C=∠F
答案:A
2.如图∠ACB=∠DFE,BF=CE,那么应补充一个条件 ,才能使△ABC≌△DEF (写出一个即可).
答案:AB∥DE,或∠B=∠E,或∠A=∠D,或 AC=DF.
3.如图,要测量河两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A,C,E在一条直线上,这时测得DE的长就是AB的长,为什么?
证明:在△ABC和△EDC中,
∠B=∠EDC=90°,
BC=DC,
∠ACB=∠ECD.
∴△ABC≌△EDC.∴DE=AB.
4.如图,小明不慎将一块三角形模具打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适 你能说明其中理由吗
答:带1去,因为有两角且夹边相等的两个三角形全等.
课堂小结:
说一说本节课都有哪些收获.
1.了解两个基本事实;有两角及夹边对应相等的两个三角形全等(简写成 “ASA”);两角和其中一角的对边对应相等的两个三角形全等.
2.运用“ASA”“AAS”证明线段和角相等的新的方法.
作业布置:
小组探讨证明全等三角形对应边上的中线,对应角的角平分线相等.
【板书设计】
基本事实:
有两角及夹边对应相等的两个三角形全等(简写成 “ASA”);两角和其中一角的对边对应相等的两个三角形全等.
应用:
证明线段和角相等提供了新的证法;
注意:
“角角边”与“角边角”的区别.
【课后反思】
先给学生独立思考的时间,培养学生独立探究,合作学习的能力.注重让学生用自己的语言归纳和表达发现的规律,指引学生对知识与方法进行回顾总结,形成良好的反思习惯.
1
