初中数学人教版八上12.3角平分线的性质第2课时 教案
文档属性
| 名称 | 初中数学人教版八上12.3角平分线的性质第2课时 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 478.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 14:01:33 | ||
图片预览


文档简介
12.3角平分线的性质第2课时
【教学目标】
1.知识与技能:了解角的平分线的判定定理;会利用角的平分线的判定进行证明与计算.
2.过程与方法:在探究角的平分线的判定定理的过程中,进一步发展学生的推理证明意识和能力.
3.情感态度与价值观:在探究作角的平分线的判定定理的过程中,培养学生探究问题的兴趣、合作交流的意识、动手操作的能力与探索精神,增强解决问题的信心,获得解决问题的成功体验.
【教学重难点】
重点:角的平分线的判定定理的证明及.
难点:角的平分线的判定的应用.
【教学方法】
情境教学法、动手实践法.
【教学过程】
新课导入:
回顾:说出角平分线的性质条件与结论.画出基本图形并分析图形特征.
创设情境,提出问题:
思考1:如图,要在S 区建一个集贸市场,使它到公路、铁路的距离相等,并且离公路和铁路的交叉处500 m. 这个集贸市场应建于何处(在图上标出它的位置,比例尺为1:20 000)?
提醒学生:根据已有的知识经验判断:在S 区建一个集贸市场,建在公路、铁路的角平分线上.
新课讲授:
(一)角平分线的判定
思考2:在这个问题中我们已有的条件和得出的结论分别是什么呢?用数学语言来描述.
条件:点到角的两边距离相等,结论:点在角的平分线上.
在学习了角平分线的性质的前提下结合实际问题,由学生动脑探索,引入新知归纳:
角平分线的判定:角的内部到角的两边的距离相等的点在角的平分线上.
几何语言:
∵PD⊥OA,PE⊥OB,PD = PE,
∴点P 在∠AOB的平分线上(OP平分∠AOB).
思考3:你能证明这个结论的正确性吗?
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=PE. 求证:点P在∠AOB的角平分线上.
证明:作射线OP,
∵PD⊥OA,PE⊥OB.
∴∠PDO=∠PEO=90°,
在Rt△PDO和Rt△PEO 中,
∴Rt△PDO≌Rt△PEO.
∴∠AOP=∠BOP
∴点P在∠AOB 角的平分线上.
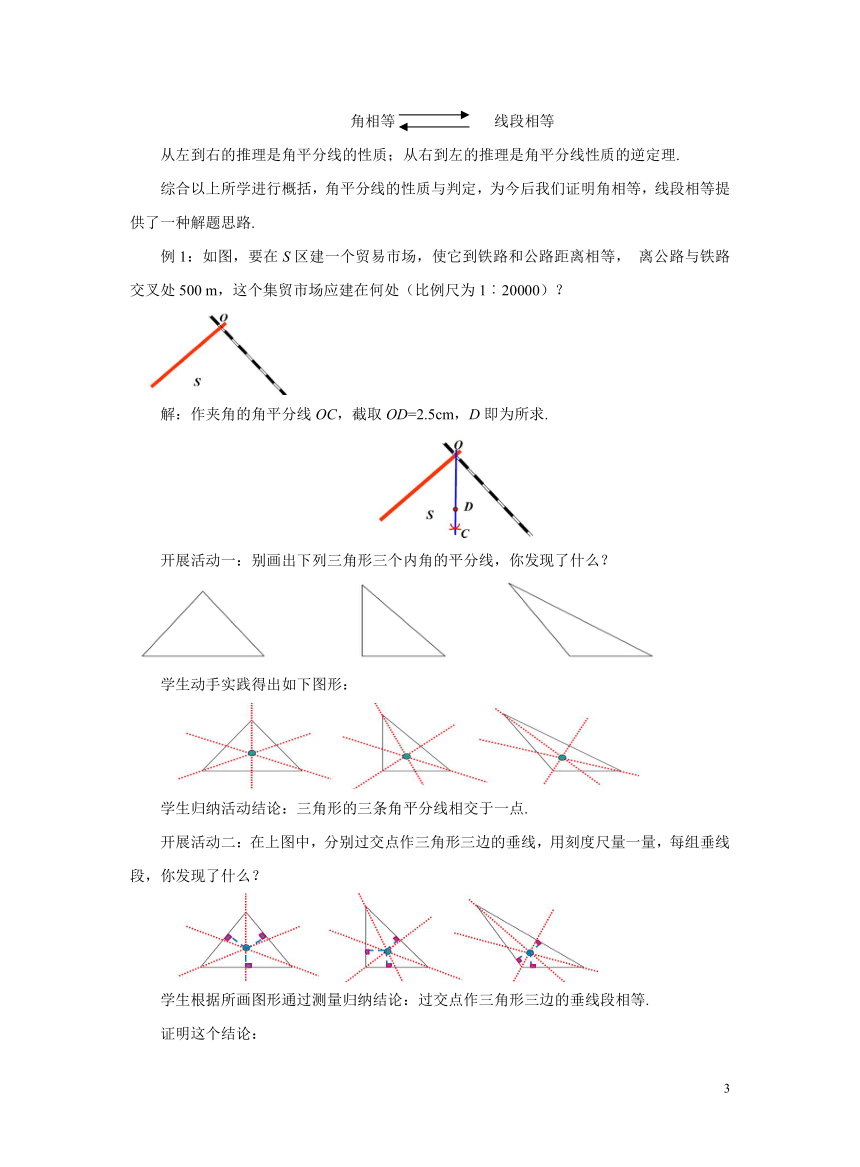
角相等 线段相等
从左到右的推理是角平分线的性质;从右到左的推理是角平分线性质的逆定理.
综合以上所学进行概括,角平分线的性质与判定,为今后我们证明角相等,线段相等提供了一种解题思路.
例1:如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500 m,这个集贸市场应建在何处(比例尺为1︰20000)?
解:作夹角的角平分线OC,截取OD=2.5cm,D即为所求.
开展活动一:别画出下列三角形三个内角的平分线,你发现了什么?
学生动手实践得出如下图形:
学生归纳活动结论:三角形的三条角平分线相交于一点.
开展活动二:在上图中,分别过交点作三角形三边的垂线,用刻度尺量一量,每组垂线段,你发现了什么?
学生根据所画图形通过测量归纳结论:过交点作三角形三边的垂线段相等.
证明这个结论:
例2:如图,△ABC 的角平分线BM,CN 相交于点P.求证:点P到三边AB,BC,CA 的距离相等.
证明:过P 点作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵BM 是△ABC的角平分线,点P 在BM 上,
∴PD = PE .
同理 PE = PF .
∴ PD = PE = PF .
即点P 到三边AB,BC,CA 的距离相等.
课堂练习:
1.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F.求证:点F在∠DAE的平分线上.
证明:过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M,
∵点F在∠BCE的平分线上,FG⊥AE,FM⊥BC,
∴FG=FM.
又∵点F在∠CBD的平分线上,FH⊥AD,FM⊥BC,
∴FM=FH.∴ FG=FH.
∴点F在∠DAE的平分线上.
2. 如图所示,表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.1处 B.2处 C.3处 D.4处
答案:D.
3.如图,在△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等.若∠A=40°,则∠BOC的度数为( )
答案:A.
解析:由已知,O到三角形三边的距离相等,所以O是三条角平分线的交点,AO,BO,CO都是角平分线,
所以有∠CBO=∠ABO= ∠ABC,
∠BCO=∠ACO= ∠ACB,
∠ABC+∠ACB=180°-40°=140°,
∠OBC+∠OCB=70°,
∠BOC=180°-70°=110°.
课堂小结:
1.本节课学习了哪些主要内容?
2.本节课是通过什么方式探究角的平分线的判定的?
3.应用角平分线的判定应注意哪些问题?
作业布置:
1. 如图所示,已知△ABC中,PE∥AB交BC于点E,PF∥AC交BC于点F,点P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.
解:AD平分∠BAC.理由如下:
∵D到PE的距离与到PF的距离相等,
∴点D在∠EPF的平分线上.
∴∠1=∠2.
又∵PE∥AB,∴∠1=∠3.
同理,∠2=∠4.
∴∠3=∠4,∴AD平分∠BAC.
2.收集2道角的平分线和判定综合运用的习题并完成解答.
3.完成本节课配套习题.
【板书设计】
角平分线的性质 角平分线的判定
图形
已知 条件 OP平分∠AOB, PD⊥OA于D, PE⊥OB于E. PD=PE, PD⊥OA于D, PE⊥OB于E,
结论 PD=PE OP平分∠AOB
【课后反思】
本节课借助于小组实践活动引导学生进行观察、猜想和验证,从而引导学生在自主探究的基础上,通过与他人的合作交流探究出角平分线的性质逆定理,这样有效地提高了课堂的教学效果,促进了学生对新知识的理解和掌握. 不足之处是少数学生在应用角平分线的性质定理和逆定理解题时,容易忽视“角平分线上的点到角两边的距离相等”这一条件,需要在今后的教学和作业中加强巩固和训练.
1
【教学目标】
1.知识与技能:了解角的平分线的判定定理;会利用角的平分线的判定进行证明与计算.
2.过程与方法:在探究角的平分线的判定定理的过程中,进一步发展学生的推理证明意识和能力.
3.情感态度与价值观:在探究作角的平分线的判定定理的过程中,培养学生探究问题的兴趣、合作交流的意识、动手操作的能力与探索精神,增强解决问题的信心,获得解决问题的成功体验.
【教学重难点】
重点:角的平分线的判定定理的证明及.
难点:角的平分线的判定的应用.
【教学方法】
情境教学法、动手实践法.
【教学过程】
新课导入:
回顾:说出角平分线的性质条件与结论.画出基本图形并分析图形特征.
创设情境,提出问题:
思考1:如图,要在S 区建一个集贸市场,使它到公路、铁路的距离相等,并且离公路和铁路的交叉处500 m. 这个集贸市场应建于何处(在图上标出它的位置,比例尺为1:20 000)?
提醒学生:根据已有的知识经验判断:在S 区建一个集贸市场,建在公路、铁路的角平分线上.
新课讲授:
(一)角平分线的判定
思考2:在这个问题中我们已有的条件和得出的结论分别是什么呢?用数学语言来描述.
条件:点到角的两边距离相等,结论:点在角的平分线上.
在学习了角平分线的性质的前提下结合实际问题,由学生动脑探索,引入新知归纳:
角平分线的判定:角的内部到角的两边的距离相等的点在角的平分线上.
几何语言:
∵PD⊥OA,PE⊥OB,PD = PE,
∴点P 在∠AOB的平分线上(OP平分∠AOB).
思考3:你能证明这个结论的正确性吗?
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=PE. 求证:点P在∠AOB的角平分线上.
证明:作射线OP,
∵PD⊥OA,PE⊥OB.
∴∠PDO=∠PEO=90°,
在Rt△PDO和Rt△PEO 中,
∴Rt△PDO≌Rt△PEO.
∴∠AOP=∠BOP
∴点P在∠AOB 角的平分线上.
角相等 线段相等
从左到右的推理是角平分线的性质;从右到左的推理是角平分线性质的逆定理.
综合以上所学进行概括,角平分线的性质与判定,为今后我们证明角相等,线段相等提供了一种解题思路.
例1:如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500 m,这个集贸市场应建在何处(比例尺为1︰20000)?
解:作夹角的角平分线OC,截取OD=2.5cm,D即为所求.
开展活动一:别画出下列三角形三个内角的平分线,你发现了什么?
学生动手实践得出如下图形:
学生归纳活动结论:三角形的三条角平分线相交于一点.
开展活动二:在上图中,分别过交点作三角形三边的垂线,用刻度尺量一量,每组垂线段,你发现了什么?
学生根据所画图形通过测量归纳结论:过交点作三角形三边的垂线段相等.
证明这个结论:
例2:如图,△ABC 的角平分线BM,CN 相交于点P.求证:点P到三边AB,BC,CA 的距离相等.
证明:过P 点作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵BM 是△ABC的角平分线,点P 在BM 上,
∴PD = PE .
同理 PE = PF .
∴ PD = PE = PF .
即点P 到三边AB,BC,CA 的距离相等.
课堂练习:
1.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F.求证:点F在∠DAE的平分线上.
证明:过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M,
∵点F在∠BCE的平分线上,FG⊥AE,FM⊥BC,
∴FG=FM.
又∵点F在∠CBD的平分线上,FH⊥AD,FM⊥BC,
∴FM=FH.∴ FG=FH.
∴点F在∠DAE的平分线上.
2. 如图所示,表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.1处 B.2处 C.3处 D.4处
答案:D.
3.如图,在△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等.若∠A=40°,则∠BOC的度数为( )
答案:A.
解析:由已知,O到三角形三边的距离相等,所以O是三条角平分线的交点,AO,BO,CO都是角平分线,
所以有∠CBO=∠ABO= ∠ABC,
∠BCO=∠ACO= ∠ACB,
∠ABC+∠ACB=180°-40°=140°,
∠OBC+∠OCB=70°,
∠BOC=180°-70°=110°.
课堂小结:
1.本节课学习了哪些主要内容?
2.本节课是通过什么方式探究角的平分线的判定的?
3.应用角平分线的判定应注意哪些问题?
作业布置:
1. 如图所示,已知△ABC中,PE∥AB交BC于点E,PF∥AC交BC于点F,点P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.
解:AD平分∠BAC.理由如下:
∵D到PE的距离与到PF的距离相等,
∴点D在∠EPF的平分线上.
∴∠1=∠2.
又∵PE∥AB,∴∠1=∠3.
同理,∠2=∠4.
∴∠3=∠4,∴AD平分∠BAC.
2.收集2道角的平分线和判定综合运用的习题并完成解答.
3.完成本节课配套习题.
【板书设计】
角平分线的性质 角平分线的判定
图形
已知 条件 OP平分∠AOB, PD⊥OA于D, PE⊥OB于E. PD=PE, PD⊥OA于D, PE⊥OB于E,
结论 PD=PE OP平分∠AOB
【课后反思】
本节课借助于小组实践活动引导学生进行观察、猜想和验证,从而引导学生在自主探究的基础上,通过与他人的合作交流探究出角平分线的性质逆定理,这样有效地提高了课堂的教学效果,促进了学生对新知识的理解和掌握. 不足之处是少数学生在应用角平分线的性质定理和逆定理解题时,容易忽视“角平分线上的点到角两边的距离相等”这一条件,需要在今后的教学和作业中加强巩固和训练.
1
