初中数学人教版八上12.3角平分线的性质第2课时 习题(含答案)
文档属性
| 名称 | 初中数学人教版八上12.3角平分线的性质第2课时 习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 348.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 14:03:20 | ||
图片预览




文档简介
12.3角平分线的性质第2课时
1. 如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A.3 B.4 C.5 D.6
2. 如图,已知于点,于点,且,,,则的度数为( )
A. B. C. D.
3. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )
A.角的内部到角的两边的距离相等的点在角的平分线上
B.角平分线上的点到这个角两边的距离相等
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
4. 已知△ABC,两个完全一样的三角板如图摆放,它们的一组对应直角边分别在AB,AC上,且这组对应边所对的顶点重合于点M,点M一定在( )
A.∠A的平分线上 B.AC边的高上
C.BC边的垂直平分线上 D.AB边的中线上
5. 如图,已知于,交于点,于点,且,如果,则度数为( )
A. 40° B.45° C.60° D. 30°
6. 如图,是内一点,且到三边、、的距离,若,度数为( )
A. 40° B.85° C.125° D. 130°
7.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=120°,则∠MAB=( )
A.30° B.35° C.45° D.60°
8.如图,AD⊥OB,BC⊥OA,垂足分别为D,C,AD与BC相交于点P,若PA=PB,则∠1与∠2的大小关系是( )
A.∠1=∠2 B.∠1>∠2 C.∠1<∠2 D.无法确定
9. 如图,在中,,,,以为圆心,以适当的长为半径作弧,交于点,交于点.分别以,为圆心,以大于的长为半径作弧,两弧在的内部相交于点,作射线,交于点,点在边上,,连接,则的周长为____.
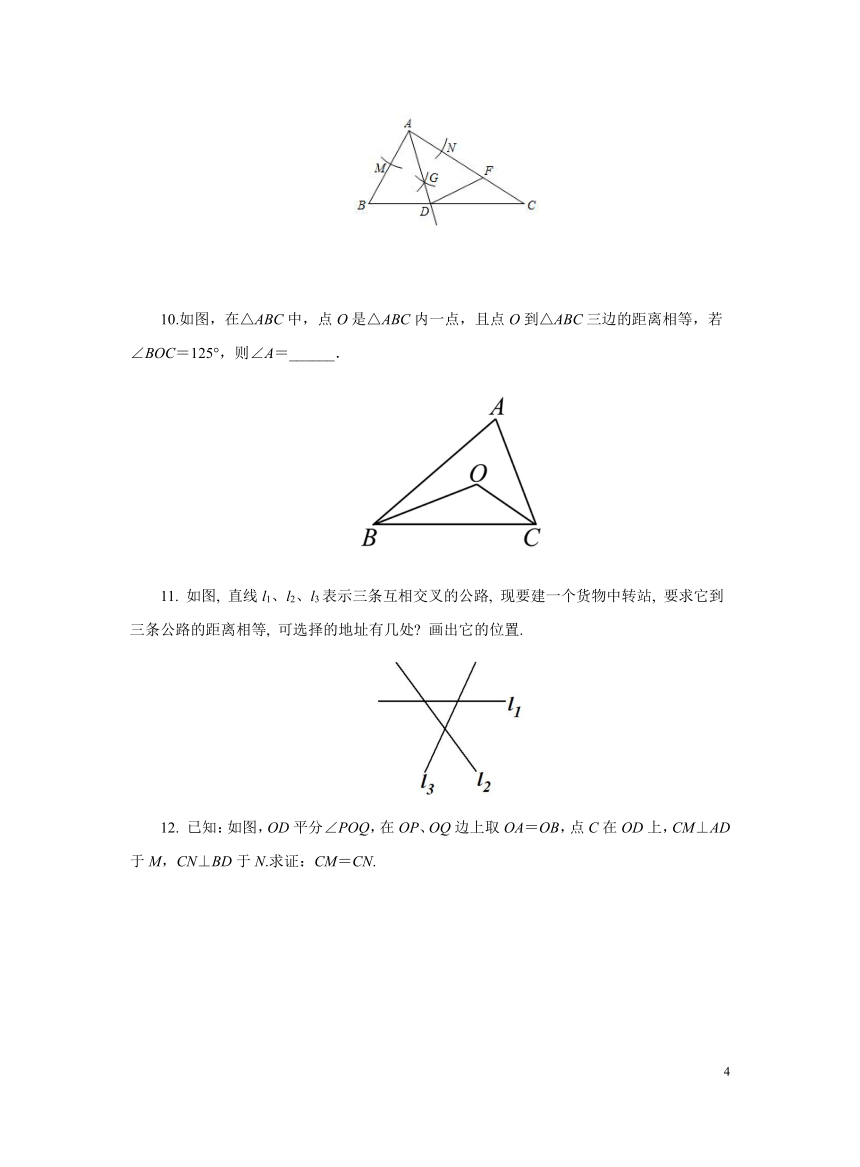
10.如图,在△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等,若∠BOC=125°,则∠A=______.
11. 如图, 直线l1、l2、l3表示三条互相交叉的公路, 现要建一个货物中转站, 要求它到三条公路的距离相等, 可选择的地址有几处 画出它的位置.
12. 已知:如图,OD平分∠POQ,在OP、OQ边上取OA=OB,点C在OD上,CM⊥AD于M,CN⊥BD于N.求证:CM=CN.
13.如图,已知:∠ABC=∠BCD=90°,CM=BM,DM平分∠ADC.
求证:(1)AM平分∠DAB;(2)AD=AB+CD.
14.如图,OM=ON,∠EMO=∠DNO,DN和EM相交于点C,DC=EC.求证:OC平分∠AOB.
15. 在△ABC中,D是BC边上的点(不与点B、C重合),连接AD.
(1)如图1,当点D是BC边上的中点时,S△ABD:S△ACD= ;
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,求S△ABD:S△ACD的值(用含m,n的代数式表示);
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连接BE,如果AC=2,AB=4,S△BDE=6,那么S△ABC= .
参考答案
1. A
解析:
作DE⊥AB于E,
∵AB=10,S△ABD =15,
∴DE=3,
∵AD平分∠BAC,∠C=90°,DE⊥AB,
∴DE=CD=3.
2.D
解析:∵BD⊥AE于B,DC⊥AF于C,且DB=DC,
∴AD是∠BAC的平分线,
∵∠BAC=40°,
∴∠CAD=∠BAC=20°,
∴∠CDA=90°-20°=70°,
∵,
∴∠CDG=∠ADG-∠CDA=130°-70°=60°.
3.A
解析:如图所示:过两把直尺的交点C作CF⊥BO与点F,由题意得CE⊥AO,
∵两把完全相同的长方形直尺,
∴CE=CF,
∴OP平分∠AOB(角的内部到角的两边的距离相等的点在这个角的平分线上).
4.A
解析:如图,
∵ME⊥AB,MF⊥AC,ME=MF,
∴M在∠BAC的角平分线上.
5.A
解析:∵于点,于点,且,
∴平分.
∵,
∴,
在中,.
6.C
解析:∵,
∴OB、OC为三角形的角平分线,
∴∠BOC=180°-(∠OBC+∠OCB)
=180°-(∠ABC+∠ACB)
=180°-(180°-∠BAC)
=90°+∠BAC=125°.
7.A
解析:作MN⊥AD于N,
∵∠B=∠C=90°,
∴AB∥CD,
∴∠DAB=180°﹣∠ADC=60°,
∵DM平分∠ADC,MN⊥AD,MC⊥CD,
∴MN=MC,
∵M是BC的中点,
∴MC=MB,
∴MN=MB,又MN⊥AD,MB⊥AB,
∴∠MAB=∠DAB=30°.
8.A
解析:∵AD⊥OB,BC⊥OA,∠ACP=∠BDP=90°,
又∵∠APC=∠BPD,PA=PB,
∴△ACP≌△BDP,
∴PC=PD,
又∵∵AD⊥OB,BC⊥OA,
∴∠1=∠2.
9.12
解析:,,,
,
由作图方法可得:平分,
,
在和中
,
∴△ABD≌△AFD(SAS),
,
的周长为:.
10.70°
解:由已知,O到三角形三边距离相等,所以O是三条角平分线交点,BO,CO都是角平分线, 所以有∠ABC=2∠CBO,∠ACB=2∠BCO,
△BOC中,∠CBO+∠BCO=180°-125°=55°,
∴∠ABC+∠ACB=2×55°=110°,
∴∠A=180-110°=70°.
11.解:根据角平分线的判定定理可以确定点P是三角形内角平分线的交点或相邻两个外角平分线的交点.∴点P有如图4个位置.
12. 证明:∵OD平分线∠POQ,
∴∠AOD=∠BOD.
在△AOD与△BOD中,
∵OA=OB,∠AOD=∠BOD,OD=OD,
∴△AOD≌△BOD.
∴∠ADO=∠BDO.
∵CM⊥AD,CN⊥BD,
∴CM=CN.
13.解:(1)过M作MH⊥AD于H,
∵DM平分∠ADC,MC⊥DC,MH⊥AD,∴CM=HM,
又∵BM=CM,∴MH=BM,
∵MH⊥AD,MB⊥AB,∴AM平分∠DAB
(2)∵∠CDM=∠HDM,∴∠CMD=∠HMD,
又∵DC⊥MC,DH⊥MH,∴DC=DH,
同理:AB=AH,
∵AD=DH+AH,∴AD=AB+CD.
14.证明:在△MOE和△NOD中,,
∴△MOE≌△NOD(ASA),∴OD=OE,
∵CD=CE,OC=OC,∴△OCD≌△OCE(SSS),
∴∠DOC=∠EOC,即OC平分∠AOB.
15. 解:(1)
过A作AE⊥BC于E,
∵点D是BC边上的中点,
∴BD=DC,
∴SABD:S△ACD=(×BD×AE):(×CD×AE)=1:1.
(2)过D作DE⊥AB于E,DF⊥AC于F,
∵AD为∠BAC的角平分线,
∴DE=DF,
∵AB=m,AC=n,
∴SABD:S△ACD=(×AB×DE):(×AC×DF)=m:n;
(3)∵AD=DE,
∴由(1)知:S△ABD:S△EBD=1:1,
∵S△BDE=6,
∴S△ABD=6,
∵AC=2,AB=4,AD平分∠CAB,
∴由(2)知:S△ABD:S△ACD=AB:AC=4:2=2:1,
∴S△ACD=3,
∴S△ABC=3+6=9.
1
1. 如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A.3 B.4 C.5 D.6
2. 如图,已知于点,于点,且,,,则的度数为( )
A. B. C. D.
3. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )
A.角的内部到角的两边的距离相等的点在角的平分线上
B.角平分线上的点到这个角两边的距离相等
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
4. 已知△ABC,两个完全一样的三角板如图摆放,它们的一组对应直角边分别在AB,AC上,且这组对应边所对的顶点重合于点M,点M一定在( )
A.∠A的平分线上 B.AC边的高上
C.BC边的垂直平分线上 D.AB边的中线上
5. 如图,已知于,交于点,于点,且,如果,则度数为( )
A. 40° B.45° C.60° D. 30°
6. 如图,是内一点,且到三边、、的距离,若,度数为( )
A. 40° B.85° C.125° D. 130°
7.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=120°,则∠MAB=( )
A.30° B.35° C.45° D.60°
8.如图,AD⊥OB,BC⊥OA,垂足分别为D,C,AD与BC相交于点P,若PA=PB,则∠1与∠2的大小关系是( )
A.∠1=∠2 B.∠1>∠2 C.∠1<∠2 D.无法确定
9. 如图,在中,,,,以为圆心,以适当的长为半径作弧,交于点,交于点.分别以,为圆心,以大于的长为半径作弧,两弧在的内部相交于点,作射线,交于点,点在边上,,连接,则的周长为____.
10.如图,在△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等,若∠BOC=125°,则∠A=______.
11. 如图, 直线l1、l2、l3表示三条互相交叉的公路, 现要建一个货物中转站, 要求它到三条公路的距离相等, 可选择的地址有几处 画出它的位置.
12. 已知:如图,OD平分∠POQ,在OP、OQ边上取OA=OB,点C在OD上,CM⊥AD于M,CN⊥BD于N.求证:CM=CN.
13.如图,已知:∠ABC=∠BCD=90°,CM=BM,DM平分∠ADC.
求证:(1)AM平分∠DAB;(2)AD=AB+CD.
14.如图,OM=ON,∠EMO=∠DNO,DN和EM相交于点C,DC=EC.求证:OC平分∠AOB.
15. 在△ABC中,D是BC边上的点(不与点B、C重合),连接AD.
(1)如图1,当点D是BC边上的中点时,S△ABD:S△ACD= ;
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,求S△ABD:S△ACD的值(用含m,n的代数式表示);
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连接BE,如果AC=2,AB=4,S△BDE=6,那么S△ABC= .
参考答案
1. A
解析:
作DE⊥AB于E,
∵AB=10,S△ABD =15,
∴DE=3,
∵AD平分∠BAC,∠C=90°,DE⊥AB,
∴DE=CD=3.
2.D
解析:∵BD⊥AE于B,DC⊥AF于C,且DB=DC,
∴AD是∠BAC的平分线,
∵∠BAC=40°,
∴∠CAD=∠BAC=20°,
∴∠CDA=90°-20°=70°,
∵,
∴∠CDG=∠ADG-∠CDA=130°-70°=60°.
3.A
解析:如图所示:过两把直尺的交点C作CF⊥BO与点F,由题意得CE⊥AO,
∵两把完全相同的长方形直尺,
∴CE=CF,
∴OP平分∠AOB(角的内部到角的两边的距离相等的点在这个角的平分线上).
4.A
解析:如图,
∵ME⊥AB,MF⊥AC,ME=MF,
∴M在∠BAC的角平分线上.
5.A
解析:∵于点,于点,且,
∴平分.
∵,
∴,
在中,.
6.C
解析:∵,
∴OB、OC为三角形的角平分线,
∴∠BOC=180°-(∠OBC+∠OCB)
=180°-(∠ABC+∠ACB)
=180°-(180°-∠BAC)
=90°+∠BAC=125°.
7.A
解析:作MN⊥AD于N,
∵∠B=∠C=90°,
∴AB∥CD,
∴∠DAB=180°﹣∠ADC=60°,
∵DM平分∠ADC,MN⊥AD,MC⊥CD,
∴MN=MC,
∵M是BC的中点,
∴MC=MB,
∴MN=MB,又MN⊥AD,MB⊥AB,
∴∠MAB=∠DAB=30°.
8.A
解析:∵AD⊥OB,BC⊥OA,∠ACP=∠BDP=90°,
又∵∠APC=∠BPD,PA=PB,
∴△ACP≌△BDP,
∴PC=PD,
又∵∵AD⊥OB,BC⊥OA,
∴∠1=∠2.
9.12
解析:,,,
,
由作图方法可得:平分,
,
在和中
,
∴△ABD≌△AFD(SAS),
,
的周长为:.
10.70°
解:由已知,O到三角形三边距离相等,所以O是三条角平分线交点,BO,CO都是角平分线, 所以有∠ABC=2∠CBO,∠ACB=2∠BCO,
△BOC中,∠CBO+∠BCO=180°-125°=55°,
∴∠ABC+∠ACB=2×55°=110°,
∴∠A=180-110°=70°.
11.解:根据角平分线的判定定理可以确定点P是三角形内角平分线的交点或相邻两个外角平分线的交点.∴点P有如图4个位置.
12. 证明:∵OD平分线∠POQ,
∴∠AOD=∠BOD.
在△AOD与△BOD中,
∵OA=OB,∠AOD=∠BOD,OD=OD,
∴△AOD≌△BOD.
∴∠ADO=∠BDO.
∵CM⊥AD,CN⊥BD,
∴CM=CN.
13.解:(1)过M作MH⊥AD于H,
∵DM平分∠ADC,MC⊥DC,MH⊥AD,∴CM=HM,
又∵BM=CM,∴MH=BM,
∵MH⊥AD,MB⊥AB,∴AM平分∠DAB
(2)∵∠CDM=∠HDM,∴∠CMD=∠HMD,
又∵DC⊥MC,DH⊥MH,∴DC=DH,
同理:AB=AH,
∵AD=DH+AH,∴AD=AB+CD.
14.证明:在△MOE和△NOD中,,
∴△MOE≌△NOD(ASA),∴OD=OE,
∵CD=CE,OC=OC,∴△OCD≌△OCE(SSS),
∴∠DOC=∠EOC,即OC平分∠AOB.
15. 解:(1)
过A作AE⊥BC于E,
∵点D是BC边上的中点,
∴BD=DC,
∴SABD:S△ACD=(×BD×AE):(×CD×AE)=1:1.
(2)过D作DE⊥AB于E,DF⊥AC于F,
∵AD为∠BAC的角平分线,
∴DE=DF,
∵AB=m,AC=n,
∴SABD:S△ACD=(×AB×DE):(×AC×DF)=m:n;
(3)∵AD=DE,
∴由(1)知:S△ABD:S△EBD=1:1,
∵S△BDE=6,
∴S△ABD=6,
∵AC=2,AB=4,AD平分∠CAB,
∴由(2)知:S△ABD:S△ACD=AB:AC=4:2=2:1,
∴S△ACD=3,
∴S△ABC=3+6=9.
1
