初中数学人教版八上13.1.2线段的垂直平分线的性质 教案
文档属性
| 名称 | 初中数学人教版八上13.1.2线段的垂直平分线的性质 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 214.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 14:08:13 | ||
图片预览



文档简介
13.1.2 线段的垂直平分线的性质
【教学目标】
1.知识与技能:理解和掌握线段垂直平分线的性质和判定,并会运用其性质和判定解决有关问题;会用尺规作已知线段的垂直平分线.
2.过程与方法:经历观察,猜想,论证,归纳等过程探究线段垂直平分线的性质,体会转化、归纳等数学思想,发展学生的推理能力.
3.情感态度与价值观:通过对线段垂直平分线性质的探究,激发学生的好奇心和求知欲,在运用数学知识解答问题的活动中获得成功的体验,建立学习的自信心.
【教学重难点】
重点:探索并证明线段垂直平分线的性质;理解线段的垂直平分线的判定定理,能运用其解决简单的问题.
难点:证明“与一条线段两个端点距离相等的点,在这条线段的垂直平分线上”;过已知直线外一点作这条直线的垂线,了解作图的道理.
【教学方法】
观察、实验法、启发式教学法.
【教学过程】
新课导入:
创设情境,提出问题:
1.说出图形轴对称的性质有哪些.
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.轴对称图形的对称轴,是任何一对对称点所连线段的垂直平分线.
2.某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等?
复习旧知后,设疑思考,激发求知的欲望,引起学习兴趣,进入新课学习.
新课讲授:
(一)线段垂直平分线的性质定理
动手探究:
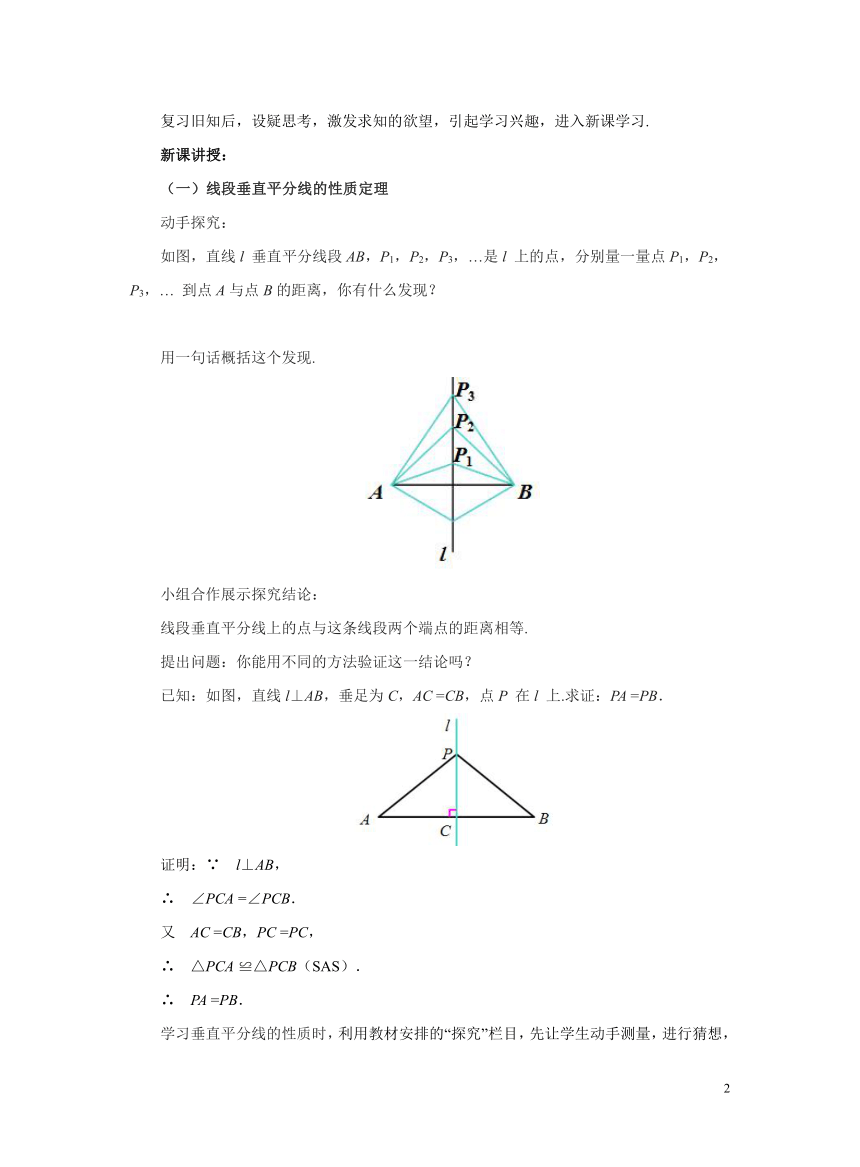
如图,直线l 垂直平分线段AB,P1,P2,P3,…是l 上的点,分别量一量点P1,P2,P3,… 到点A与点B的距离,你有什么发现?
用一句话概括这个发现.
小组合作展示探究结论:
线段垂直平分线上的点与这条线段两个端点的距离相等.
提出问题:你能用不同的方法验证这一结论吗?
已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.求证:PA =PB.
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
学习垂直平分线的性质时,利用教材安排的“探究”栏目,先让学生动手测量,进行猜想,然后通过对折进行验证,最后引导学生运用三角形全等进行证明,让学生经历线段垂直平分线性质的探索和证明的全过程,积累探索经验,提高研究图形性质的能力.
例1:如图,在△ABC中,AB=AC=20 cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35 cm,求BC的长.
解:∵△DBC的周长为BC+BD+CD=35 cm,
又∵DE垂直平分AB,∴AD=BD,
∴BC+AD+CD=35 cm.
∵AC=AD+DC=20 cm,
∴BC=35-20=15(cm).
方法归纳:利用线段垂直平分线的性质,不需要证明三角形全等.证明更便捷.
结论:
线段垂直平分线的性质:线段垂直平分线上的点与这条线段两个端点的距离相等.
几何语言:
∵点P 在AB 的垂直平分线上,∴PA =PB.
(二)线段垂直平分线的判定定理
反过来,
线段垂直平分线的判定:
到线段两个端点的距离相等的点在这条线段的垂直平分线上.
几何语言:
∵ PA =PB,∴ 点P 在AB 的垂直平分线上.
已知:如图,在△ABP中,PA =PB.求证:点P 在线段AB 的垂直平分线上.
证明:过点P 作线段AB 的垂线PC,
垂足为C.则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.
例2:如图,AB =AC,MB =MC.直线AM 是线段BC 的垂直平分线吗?
解:∵ AB =AC,
∴ 点A 在BC 的垂直平分线.
∵ MB =MC,
∵ 点M 在BC 的垂直平分线上,
∴ 直线AM 是线段BC 的垂直平分线.
解决问题:
某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等?快动手做一做吧.
答案:建在△ABC三边的垂直平分线的交点上.
课堂练习:
如图,在△ABC 中,BC =8,AB 的中垂线交BC 于D,AC 的中垂线交BC 与E,则△ADE 的周长等于______.
答案:8
(三)尺规作图
例3:尺规作图:经过已知直线外一点作这条直线的垂线.
已知:直线AB和AB外一点C .
已知:直线AB和AB外一点C .
作法:
作法:(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C 为圆心,CK长为半径作弧,交AB于点D和点E.
(3)分别以点D和点E为圆心,大于 DE的长为半径作弧,两弧相交于点F.
(4)作直线CF.
直线CF.即为所求.
思考:
(1)为什么任意取一点K,使点K与点C 在直线两旁?
(2)为什么要以大于 的长为半径作弧?
(3)为什么直线CF 就是所求作的垂线?
作图依据是垂直平分线的性质和判定,问题与(1)是创造垂直平分线的条件,问题(2)是当半径取值不大于它时,不存在弧的交点,问题(3)此时符合垂直平分线的判定定理.
让学生在动手探究和思考中理解作图的原理,而不是死记硬背.
如图,△ABC和△A′B′C′关于直线l对称,请用无刻度的直尺作出它们的对称轴.
解:延长BC、B′C′交于点P,延长AC,A'C'交于点Q,连接PQ,则直线PQ即为所要求作的直线l.
及时引导学生归纳发现:
如果成轴对称的两个图形对称点连线段(或延长线)相交,那么交点必定在对称轴上.
延伸:
作轴对称图形的对称轴的方法:
1.作对应点连线的垂直平分线;
2.折叠法;
3.延长对应线段确定其交点,两个这样的交点确定图形的对称轴.
课堂练习:
1.如图,点A和点B关于某条直线成轴对称,你能作出这条直线吗?
作法:
(1)分别以点A,B为圆心,以大于1/2 AB的长为半径作弧,两弧交于C,D两点.
(2)作直线CD. CD即为所求.
2.如图,角是轴对称图形吗?如果是,它的对称轴是什么?
角是轴对称图形,角平分线所在的直线就是角的对称轴.
课堂小结:
说一说本节课都有哪些收获.
垂直平分线的性质与判定定理;作一条线段的垂直平分线;过一点作已知直线的垂线.
学会运用线段垂直平分线的性质证明线段相等,体会其证明线段相等的简捷性,防止学生在能利用线段垂直平分线的性质证明线段相等时,还用三角形全等的方法来证明.
作业布置:
1.完成本节配套习题.
2.在课本上找一个轴对称图形,用不同的方法画出图形的对称轴.
【板书设计】
垂直平分线的性质:线段的垂直平分线上的点到线段的两个端点的距离相等
作用,见垂直平分线,得线段相等.
垂直平分线的判定:到线段的两个端点距离相等的点在线段的垂直平分线上.
方法:作垂直证平分,作平分证垂直.
尺规作图:
作一条线段的垂直平分线;过一点作已知直线的垂线.
【课后反思】
在一定的情境中,引导学生借助已有的知识和经验,借助图形的直观,通过操作、度量、运用合情推理或图形运动等方法,探索发现图形可能具有的性质,然后再进行证明,这与单纯给出“已知、求证、证明”的方式研究图形性质是有区别的.两者相比,前者更加有利于学生在获取有关知识的过程中,不断提高研究几何图形性质的能力,发展创新意识和创新能力.
1
【教学目标】
1.知识与技能:理解和掌握线段垂直平分线的性质和判定,并会运用其性质和判定解决有关问题;会用尺规作已知线段的垂直平分线.
2.过程与方法:经历观察,猜想,论证,归纳等过程探究线段垂直平分线的性质,体会转化、归纳等数学思想,发展学生的推理能力.
3.情感态度与价值观:通过对线段垂直平分线性质的探究,激发学生的好奇心和求知欲,在运用数学知识解答问题的活动中获得成功的体验,建立学习的自信心.
【教学重难点】
重点:探索并证明线段垂直平分线的性质;理解线段的垂直平分线的判定定理,能运用其解决简单的问题.
难点:证明“与一条线段两个端点距离相等的点,在这条线段的垂直平分线上”;过已知直线外一点作这条直线的垂线,了解作图的道理.
【教学方法】
观察、实验法、启发式教学法.
【教学过程】
新课导入:
创设情境,提出问题:
1.说出图形轴对称的性质有哪些.
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.轴对称图形的对称轴,是任何一对对称点所连线段的垂直平分线.
2.某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等?
复习旧知后,设疑思考,激发求知的欲望,引起学习兴趣,进入新课学习.
新课讲授:
(一)线段垂直平分线的性质定理
动手探究:
如图,直线l 垂直平分线段AB,P1,P2,P3,…是l 上的点,分别量一量点P1,P2,P3,… 到点A与点B的距离,你有什么发现?
用一句话概括这个发现.
小组合作展示探究结论:
线段垂直平分线上的点与这条线段两个端点的距离相等.
提出问题:你能用不同的方法验证这一结论吗?
已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.求证:PA =PB.
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
学习垂直平分线的性质时,利用教材安排的“探究”栏目,先让学生动手测量,进行猜想,然后通过对折进行验证,最后引导学生运用三角形全等进行证明,让学生经历线段垂直平分线性质的探索和证明的全过程,积累探索经验,提高研究图形性质的能力.
例1:如图,在△ABC中,AB=AC=20 cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35 cm,求BC的长.
解:∵△DBC的周长为BC+BD+CD=35 cm,
又∵DE垂直平分AB,∴AD=BD,
∴BC+AD+CD=35 cm.
∵AC=AD+DC=20 cm,
∴BC=35-20=15(cm).
方法归纳:利用线段垂直平分线的性质,不需要证明三角形全等.证明更便捷.
结论:
线段垂直平分线的性质:线段垂直平分线上的点与这条线段两个端点的距离相等.
几何语言:
∵点P 在AB 的垂直平分线上,∴PA =PB.
(二)线段垂直平分线的判定定理
反过来,
线段垂直平分线的判定:
到线段两个端点的距离相等的点在这条线段的垂直平分线上.
几何语言:
∵ PA =PB,∴ 点P 在AB 的垂直平分线上.
已知:如图,在△ABP中,PA =PB.求证:点P 在线段AB 的垂直平分线上.
证明:过点P 作线段AB 的垂线PC,
垂足为C.则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.
例2:如图,AB =AC,MB =MC.直线AM 是线段BC 的垂直平分线吗?
解:∵ AB =AC,
∴ 点A 在BC 的垂直平分线.
∵ MB =MC,
∵ 点M 在BC 的垂直平分线上,
∴ 直线AM 是线段BC 的垂直平分线.
解决问题:
某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等?快动手做一做吧.
答案:建在△ABC三边的垂直平分线的交点上.
课堂练习:
如图,在△ABC 中,BC =8,AB 的中垂线交BC 于D,AC 的中垂线交BC 与E,则△ADE 的周长等于______.
答案:8
(三)尺规作图
例3:尺规作图:经过已知直线外一点作这条直线的垂线.
已知:直线AB和AB外一点C .
已知:直线AB和AB外一点C .
作法:
作法:(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C 为圆心,CK长为半径作弧,交AB于点D和点E.
(3)分别以点D和点E为圆心,大于 DE的长为半径作弧,两弧相交于点F.
(4)作直线CF.
直线CF.即为所求.
思考:
(1)为什么任意取一点K,使点K与点C 在直线两旁?
(2)为什么要以大于 的长为半径作弧?
(3)为什么直线CF 就是所求作的垂线?
作图依据是垂直平分线的性质和判定,问题与(1)是创造垂直平分线的条件,问题(2)是当半径取值不大于它时,不存在弧的交点,问题(3)此时符合垂直平分线的判定定理.
让学生在动手探究和思考中理解作图的原理,而不是死记硬背.
如图,△ABC和△A′B′C′关于直线l对称,请用无刻度的直尺作出它们的对称轴.
解:延长BC、B′C′交于点P,延长AC,A'C'交于点Q,连接PQ,则直线PQ即为所要求作的直线l.
及时引导学生归纳发现:
如果成轴对称的两个图形对称点连线段(或延长线)相交,那么交点必定在对称轴上.
延伸:
作轴对称图形的对称轴的方法:
1.作对应点连线的垂直平分线;
2.折叠法;
3.延长对应线段确定其交点,两个这样的交点确定图形的对称轴.
课堂练习:
1.如图,点A和点B关于某条直线成轴对称,你能作出这条直线吗?
作法:
(1)分别以点A,B为圆心,以大于1/2 AB的长为半径作弧,两弧交于C,D两点.
(2)作直线CD. CD即为所求.
2.如图,角是轴对称图形吗?如果是,它的对称轴是什么?
角是轴对称图形,角平分线所在的直线就是角的对称轴.
课堂小结:
说一说本节课都有哪些收获.
垂直平分线的性质与判定定理;作一条线段的垂直平分线;过一点作已知直线的垂线.
学会运用线段垂直平分线的性质证明线段相等,体会其证明线段相等的简捷性,防止学生在能利用线段垂直平分线的性质证明线段相等时,还用三角形全等的方法来证明.
作业布置:
1.完成本节配套习题.
2.在课本上找一个轴对称图形,用不同的方法画出图形的对称轴.
【板书设计】
垂直平分线的性质:线段的垂直平分线上的点到线段的两个端点的距离相等
作用,见垂直平分线,得线段相等.
垂直平分线的判定:到线段的两个端点距离相等的点在线段的垂直平分线上.
方法:作垂直证平分,作平分证垂直.
尺规作图:
作一条线段的垂直平分线;过一点作已知直线的垂线.
【课后反思】
在一定的情境中,引导学生借助已有的知识和经验,借助图形的直观,通过操作、度量、运用合情推理或图形运动等方法,探索发现图形可能具有的性质,然后再进行证明,这与单纯给出“已知、求证、证明”的方式研究图形性质是有区别的.两者相比,前者更加有利于学生在获取有关知识的过程中,不断提高研究几何图形性质的能力,发展创新意识和创新能力.
1
