初中数学人教版八上13.1.2线段的垂直平分线的性质 习题(含答案)
文档属性
| 名称 | 初中数学人教版八上13.1.2线段的垂直平分线的性质 习题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 201.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 15:25:08 | ||
图片预览




文档简介
13.1.2线段的垂直平分线的性质
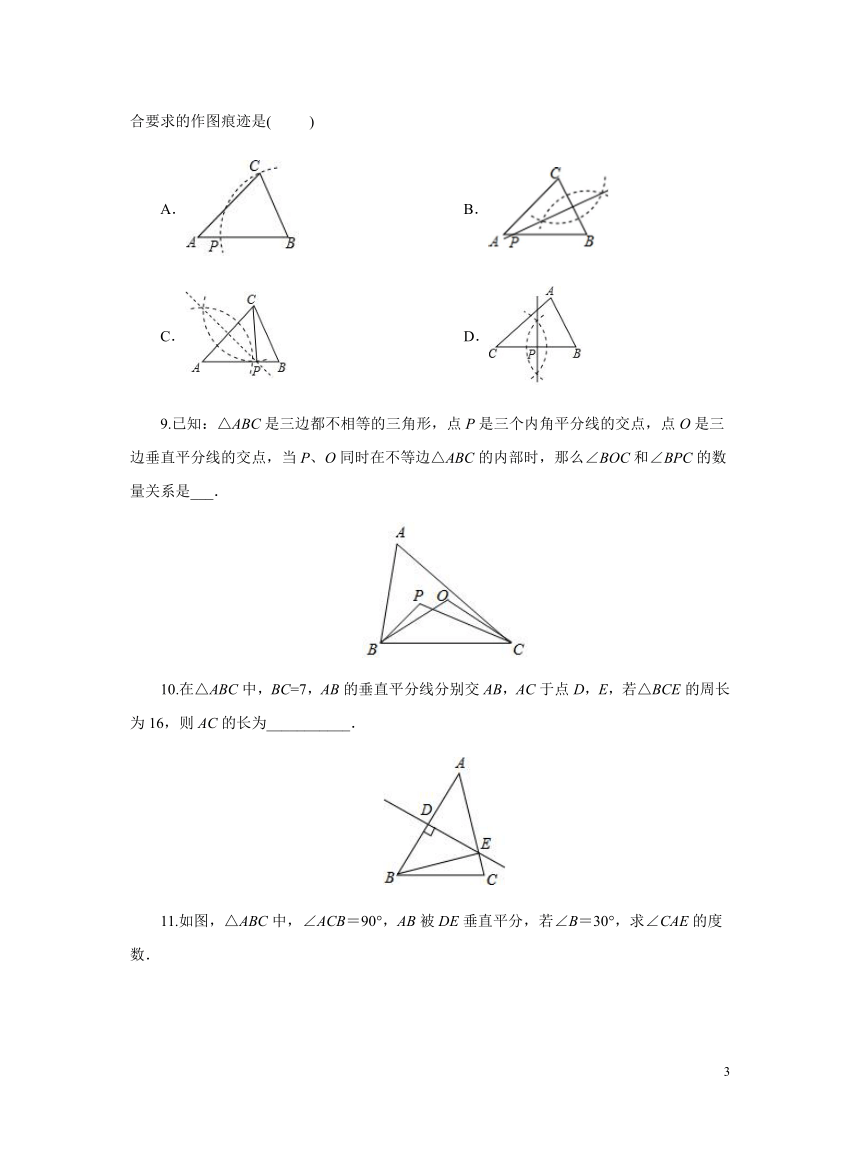
1.如图,在△ABC中,BC的垂直平分线分别交AC,BC于点D,E,若△ABC的周长为17,BE=3,则△ABD的周长为( )
A.6 B.10 C.11 D.20
2.如图,在△ABC中,AB=3,BC=5,AC的垂直平分线分别交BC,AC于点D,E,则△ABD的周长为( )
A.8 B.11 C.16 D.17
3.如图,已知△ABC,求作一点O,使O到的两边的距离相等,且OA=OB、下列确定O点的方法正确的是( )
A.O为∠A,∠B两角平分线的交点 B.O为两边上的高的交点
C.O为两边的垂直平分线的交点
D.O为∠A的角平分线与AB的垂直平分线的交点
4.到三角形三个顶点距离相等的点是( )
A.三角形三边垂直平分线的交点 B.三角形三条高的交点
C.三角形三条中线的交点 D.三角形三条角平分线的交点
5.如图,根据图中尺规作图痕迹,计算∠1的度数是( )
A.22° B.32° C.34° D.68°
6.三角形纸片DEF上有一点M,量得ME=2,MF=2,则点M一定( )
A.是边DE的中点 B.在边DE的中线上
C.在边DE的高上 D.在边EF的垂直平分线上
7.如图,△ABC中,∠B=66°,∠C=28°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N作直线MN,交BC于点D,连结AD,则∠BAD的度数为( )
A.65° B.58° C.55° D.44°
8.如图,已知△ABC(AC<AB),用尺规在AB上确定一点P,使PB+PC=AB,则符合要求的作图痕迹是( )
A. B.
C. D.
9.已知:△ABC是三边都不相等的三角形,点P是三个内角平分线的交点,点O是三边垂直平分线的交点,当P、O同时在不等边△ABC的内部时,那么∠BOC和∠BPC的数量关系是___.
10.在△ABC中,BC=7,AB的垂直平分线分别交AB,AC于点D,E,若△BCE的周长为16,则AC的长为___________.
11.如图,△ABC中,∠ACB=90°,AB被DE垂直平分,若∠B=30°,求∠CAE的度数.
12.如图,在△ABC中,DM,EN分别垂直平分边AC和边BC,交边AB于M,N两点,DM与EN相交于点F.∠MFN=68°,求∠MCN的度数.
13.如图,直线l与m分别是边AC和BC的垂直平分线,它们分别交边AB于点M和点N.
(1)若,则△CMN的周长是多少?为什么?
(2)若,求∠MCN的度数.
14.如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AP、BP,BP⊥AP,延长AP交BC的延长线于点F. 已知AD=2 cm,BC=5 cm.
(1)求证:FC=AD;
(2)求AB的长.
15.已知在△ABQ中,∠QAB的平分线AD与BQ的垂直平分线DE交于点D,DP⊥AB于P,DN⊥AQ的延长线于N.
(1)证明:BP=QN;
(2)当∠BAQ=70°时,求∠DQB的度数.
参考答案
1.C
解析:∵DE为BC的垂直平分线,
∴BD=CD,BE=CE=3,
∵△ABC的周长为16,BE=3,
∴AB+AC=11,
∴的周长为.
2.A
解析:∵DE是线段AC的垂直平分线,
∴,
∴的周长.
3.D
解析:∵O到∠A的两边的距离相等,
∴O为∠A的角平分线;
∵OA=OB,
∴O为AB的垂直平分线,
∴O为∠A的角平分线与AB的垂直平分线的交点.
4.A
解析:线段的垂直平分线上的点到线段的两个端点的距离相等,
到三角形三个顶点的距离相等的点是三角形三边垂直平分线的交点.
5.A
解析:由尺规作图痕迹,可知:CD是AB的垂直平分线,
∴AC=BC,
∴∠1=∠ABC=90°-68°=22°.
6.D
解析:∵ME=2 ,MF=2
∴点M一定在边EF的垂直平分线上.
7.B
解:由题意可得:MN是AC的垂直平分线,
则AD=DC,故∠C=∠DAC=28°,
∴∠BAC=180°-∠B-∠C=86°,
∴∠BAD=∠BAC-∠CAD=58°.
8.C
解析:∵点P在AB上,∴PB+PA=AB,
又∵PB+PC=AB,∴PC=PA,
∴点P在线段AC的垂直平分线上,
且线段AC的垂直平分线交AB于点P.
∴选项C符合要求.
9.∠BOC=4∠BPC-360°
解析:平分,平分,
,,
,
即;
如图,连接.
点是这个三角形三边垂直平分线的交点,
,
,,,
,,
,
.
10.9
解:∵DE是AB的垂直平分线,
∴EA=EB,
由题意得,BC+CE+BE=16,
则BC+CE+AE=16,即BC+AC=16,又BC=7,
∴AC=16-BC=9.
11.解:∵DE垂直平分AB,∴EA=EB,
∴∠EAB=∠B=30°,
∵∠C=90°,∴∠CAB=90°-∠EAB=60°,
∴∠CAE=60°﹣30°=30°.
12.解:∵DM、EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,∠ADM=∠CDM=90°,∠ADM=∠CDM=90°,
在Rt△AMD和Rt△CMD中,,
所以Rt△AMD≌Rt△CMD,
∴∠AMD=∠NMF,
同理,∠BNE=∠MNF,
△MNF中,∠MNF+∠NMF=180°﹣∠MFN=180°﹣68°=112°,
∴∠AMD+∠BNE=∠MNF+∠NMF=112°,
∴∠A+∠B=90°﹣∠AMD+90°﹣∠BNE=180°﹣112°=68°,
∵AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∴∠MCN=180°﹣2(∠A+∠B)=180°﹣2×68°=44°.
13.解:(1)△CMN的周长为10
∵l是AC的垂直平分线,∴CM=AM,
同理CN=BN
∴△CMN的周长=CM+CN+MN=AM+MN+BN=AB=10.
(2)∵l是AC的垂直平分线∴∠MCA=∠A,
同理∠BCN=∠B.
∴∠CMN=2∠A,∠CNM=2∠B,
∵∠CMN+∠CNM+∠NCM=180°,
∴∠NCM+2∠A+2∠B=180°,①
∵∠MCN+∠ACM+∠NCA=125°,
∴∠MCN+∠A+∠B=125°,②
联立①②,解得:∠MCN=70°.
14.解:(1)∵AD∥BC,∴∠ADC=∠PCF ,
∵P是CD的中点,∴DP=PC ,
∵在△ADP与△FCP中, ,
∴△ADP≌△FCP ,∴FC=AD ;
(2)∵△ADP≌△FCP,∴AP=PF,AD=CF ,
又∵BP⊥AP ,∴BP是线段AF的垂直平分线,
∴AB=BF=BC+CF,
∵AD=CF ,∴AB=BC+AD=5+2=7(cm).
15.解:(1)证明:连接BD、QD,如图所示:
∵AD是∠CAB的平分线,DP⊥AB,DN⊥AQ,∴DP=DN,
∵DE垂直平分线BQ,∴DB=DQ,
在Rt△DPB和Rt△DNQ中,
∴Rt△DPB≌Rt△DNQ,
∴BP=QN;
(2)由(1)得:∠BDP=∠QDN,
∵AD是∠QAB的平分线,DP⊥AB,DN⊥AQ,∴DP=DN,
在Rt△DPA和Rt△DNA中,
∴Rt△DPA≌Rt△DNA,∴∠ADP=∠ADN
∵∠BAQ=70°,∴∠PDN=360°-90°×2-70°=110°,∠ADP=∠ADN=110°÷2=55°,
∴∠BDQ=∠PDN=110°
∵AD是BQ的垂直平分线,∴∠EDQ=55°
∴∠DQB=90°-∠EDQ=90°-55°=35°.
1
1.如图,在△ABC中,BC的垂直平分线分别交AC,BC于点D,E,若△ABC的周长为17,BE=3,则△ABD的周长为( )
A.6 B.10 C.11 D.20
2.如图,在△ABC中,AB=3,BC=5,AC的垂直平分线分别交BC,AC于点D,E,则△ABD的周长为( )
A.8 B.11 C.16 D.17
3.如图,已知△ABC,求作一点O,使O到的两边的距离相等,且OA=OB、下列确定O点的方法正确的是( )
A.O为∠A,∠B两角平分线的交点 B.O为两边上的高的交点
C.O为两边的垂直平分线的交点
D.O为∠A的角平分线与AB的垂直平分线的交点
4.到三角形三个顶点距离相等的点是( )
A.三角形三边垂直平分线的交点 B.三角形三条高的交点
C.三角形三条中线的交点 D.三角形三条角平分线的交点
5.如图,根据图中尺规作图痕迹,计算∠1的度数是( )
A.22° B.32° C.34° D.68°
6.三角形纸片DEF上有一点M,量得ME=2,MF=2,则点M一定( )
A.是边DE的中点 B.在边DE的中线上
C.在边DE的高上 D.在边EF的垂直平分线上
7.如图,△ABC中,∠B=66°,∠C=28°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N作直线MN,交BC于点D,连结AD,则∠BAD的度数为( )
A.65° B.58° C.55° D.44°
8.如图,已知△ABC(AC<AB),用尺规在AB上确定一点P,使PB+PC=AB,则符合要求的作图痕迹是( )
A. B.
C. D.
9.已知:△ABC是三边都不相等的三角形,点P是三个内角平分线的交点,点O是三边垂直平分线的交点,当P、O同时在不等边△ABC的内部时,那么∠BOC和∠BPC的数量关系是___.
10.在△ABC中,BC=7,AB的垂直平分线分别交AB,AC于点D,E,若△BCE的周长为16,则AC的长为___________.
11.如图,△ABC中,∠ACB=90°,AB被DE垂直平分,若∠B=30°,求∠CAE的度数.
12.如图,在△ABC中,DM,EN分别垂直平分边AC和边BC,交边AB于M,N两点,DM与EN相交于点F.∠MFN=68°,求∠MCN的度数.
13.如图,直线l与m分别是边AC和BC的垂直平分线,它们分别交边AB于点M和点N.
(1)若,则△CMN的周长是多少?为什么?
(2)若,求∠MCN的度数.
14.如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AP、BP,BP⊥AP,延长AP交BC的延长线于点F. 已知AD=2 cm,BC=5 cm.
(1)求证:FC=AD;
(2)求AB的长.
15.已知在△ABQ中,∠QAB的平分线AD与BQ的垂直平分线DE交于点D,DP⊥AB于P,DN⊥AQ的延长线于N.
(1)证明:BP=QN;
(2)当∠BAQ=70°时,求∠DQB的度数.
参考答案
1.C
解析:∵DE为BC的垂直平分线,
∴BD=CD,BE=CE=3,
∵△ABC的周长为16,BE=3,
∴AB+AC=11,
∴的周长为.
2.A
解析:∵DE是线段AC的垂直平分线,
∴,
∴的周长.
3.D
解析:∵O到∠A的两边的距离相等,
∴O为∠A的角平分线;
∵OA=OB,
∴O为AB的垂直平分线,
∴O为∠A的角平分线与AB的垂直平分线的交点.
4.A
解析:线段的垂直平分线上的点到线段的两个端点的距离相等,
到三角形三个顶点的距离相等的点是三角形三边垂直平分线的交点.
5.A
解析:由尺规作图痕迹,可知:CD是AB的垂直平分线,
∴AC=BC,
∴∠1=∠ABC=90°-68°=22°.
6.D
解析:∵ME=2 ,MF=2
∴点M一定在边EF的垂直平分线上.
7.B
解:由题意可得:MN是AC的垂直平分线,
则AD=DC,故∠C=∠DAC=28°,
∴∠BAC=180°-∠B-∠C=86°,
∴∠BAD=∠BAC-∠CAD=58°.
8.C
解析:∵点P在AB上,∴PB+PA=AB,
又∵PB+PC=AB,∴PC=PA,
∴点P在线段AC的垂直平分线上,
且线段AC的垂直平分线交AB于点P.
∴选项C符合要求.
9.∠BOC=4∠BPC-360°
解析:平分,平分,
,,
,
即;
如图,连接.
点是这个三角形三边垂直平分线的交点,
,
,,,
,,
,
.
10.9
解:∵DE是AB的垂直平分线,
∴EA=EB,
由题意得,BC+CE+BE=16,
则BC+CE+AE=16,即BC+AC=16,又BC=7,
∴AC=16-BC=9.
11.解:∵DE垂直平分AB,∴EA=EB,
∴∠EAB=∠B=30°,
∵∠C=90°,∴∠CAB=90°-∠EAB=60°,
∴∠CAE=60°﹣30°=30°.
12.解:∵DM、EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,∠ADM=∠CDM=90°,∠ADM=∠CDM=90°,
在Rt△AMD和Rt△CMD中,,
所以Rt△AMD≌Rt△CMD,
∴∠AMD=∠NMF,
同理,∠BNE=∠MNF,
△MNF中,∠MNF+∠NMF=180°﹣∠MFN=180°﹣68°=112°,
∴∠AMD+∠BNE=∠MNF+∠NMF=112°,
∴∠A+∠B=90°﹣∠AMD+90°﹣∠BNE=180°﹣112°=68°,
∵AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∴∠MCN=180°﹣2(∠A+∠B)=180°﹣2×68°=44°.
13.解:(1)△CMN的周长为10
∵l是AC的垂直平分线,∴CM=AM,
同理CN=BN
∴△CMN的周长=CM+CN+MN=AM+MN+BN=AB=10.
(2)∵l是AC的垂直平分线∴∠MCA=∠A,
同理∠BCN=∠B.
∴∠CMN=2∠A,∠CNM=2∠B,
∵∠CMN+∠CNM+∠NCM=180°,
∴∠NCM+2∠A+2∠B=180°,①
∵∠MCN+∠ACM+∠NCA=125°,
∴∠MCN+∠A+∠B=125°,②
联立①②,解得:∠MCN=70°.
14.解:(1)∵AD∥BC,∴∠ADC=∠PCF ,
∵P是CD的中点,∴DP=PC ,
∵在△ADP与△FCP中, ,
∴△ADP≌△FCP ,∴FC=AD ;
(2)∵△ADP≌△FCP,∴AP=PF,AD=CF ,
又∵BP⊥AP ,∴BP是线段AF的垂直平分线,
∴AB=BF=BC+CF,
∵AD=CF ,∴AB=BC+AD=5+2=7(cm).
15.解:(1)证明:连接BD、QD,如图所示:
∵AD是∠CAB的平分线,DP⊥AB,DN⊥AQ,∴DP=DN,
∵DE垂直平分线BQ,∴DB=DQ,
在Rt△DPB和Rt△DNQ中,
∴Rt△DPB≌Rt△DNQ,
∴BP=QN;
(2)由(1)得:∠BDP=∠QDN,
∵AD是∠QAB的平分线,DP⊥AB,DN⊥AQ,∴DP=DN,
在Rt△DPA和Rt△DNA中,
∴Rt△DPA≌Rt△DNA,∴∠ADP=∠ADN
∵∠BAQ=70°,∴∠PDN=360°-90°×2-70°=110°,∠ADP=∠ADN=110°÷2=55°,
∴∠BDQ=∠PDN=110°
∵AD是BQ的垂直平分线,∴∠EDQ=55°
∴∠DQB=90°-∠EDQ=90°-55°=35°.
1
