初中数学人教版八上13.3.1等腰三角形第1课时 教案
文档属性
| 名称 | 初中数学人教版八上13.3.1等腰三角形第1课时 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 303.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 15:28:41 | ||
图片预览



文档简介
13.3.1等腰三角形第1课时
【教学目标】
1.探索并证明等腰三角形的两个性质,能利用性质证明两个角相等或两条线段相等.
2.结合等腰三角形性质的探索与证明过程,体会轴对称在研究几何问题中的作用,了解作辅助线的技巧,发展“转化”及“分类讨论”的数学思想.
3.引导学生对图形观察、发现,激发学生的求知欲望和学习兴趣,帮助学生养成良好的学习习惯和勤于思考、勇于探索的的思想品质,建立学习的自信心.
【教学重难点】
重点:1.等腰三角形的概念及性质;2.等腰三角形性质的应用.
难点:等腰三角形三线合一的性质的理解及其应用.
【教学方法】
探究实践法、小组合作法、合情推理法.
【教学过程】
新课导入:
创设情境,提出问题:
欣赏下列图片,找出图片中的三角形,观察它们的特点.
观察图片,从生活常见的现象入手,发现特点,进入新课学习.
新课讲授:
(一)等腰三角形的性质1
动手探究:
如图所示,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC 有什么特点?
通过动手体验,小组合作展示探究结论:
所得三角形是等腰三角形,折痕所在直线是对称轴,垂直平分三角形的边,剪痕是三角形相等的两条边.
等腰三角形是轴对称图形.
找一找:把剪出的等腰△ABC沿折痕对折,找出其中重合的线段和角.你能发现等腰三角形的性质吗?
重合线段:AB与AC,BD与CD,AD与AD
重合的边:∠B与∠C,∠BAD与∠CAD,∠ADB与∠ADC.
已知: 如图,在△ABC中,AB=AC.
求证: ∠B=∠C.
证明: 作底边的中线AD, 则BD=CD.
在△BAD和△CAD中,
∴ △BAD≌ △CAD,
∴ ∠B= ∠C.
思考: 还有哪些方法可以得到∠B=∠C?
方法二:
证明: 作顶角的平分线AD,则有∠1=∠2.
在△ABD和△ACD中,
∴ △ABD≌ △ACD ,
∴ ∠B=∠C .
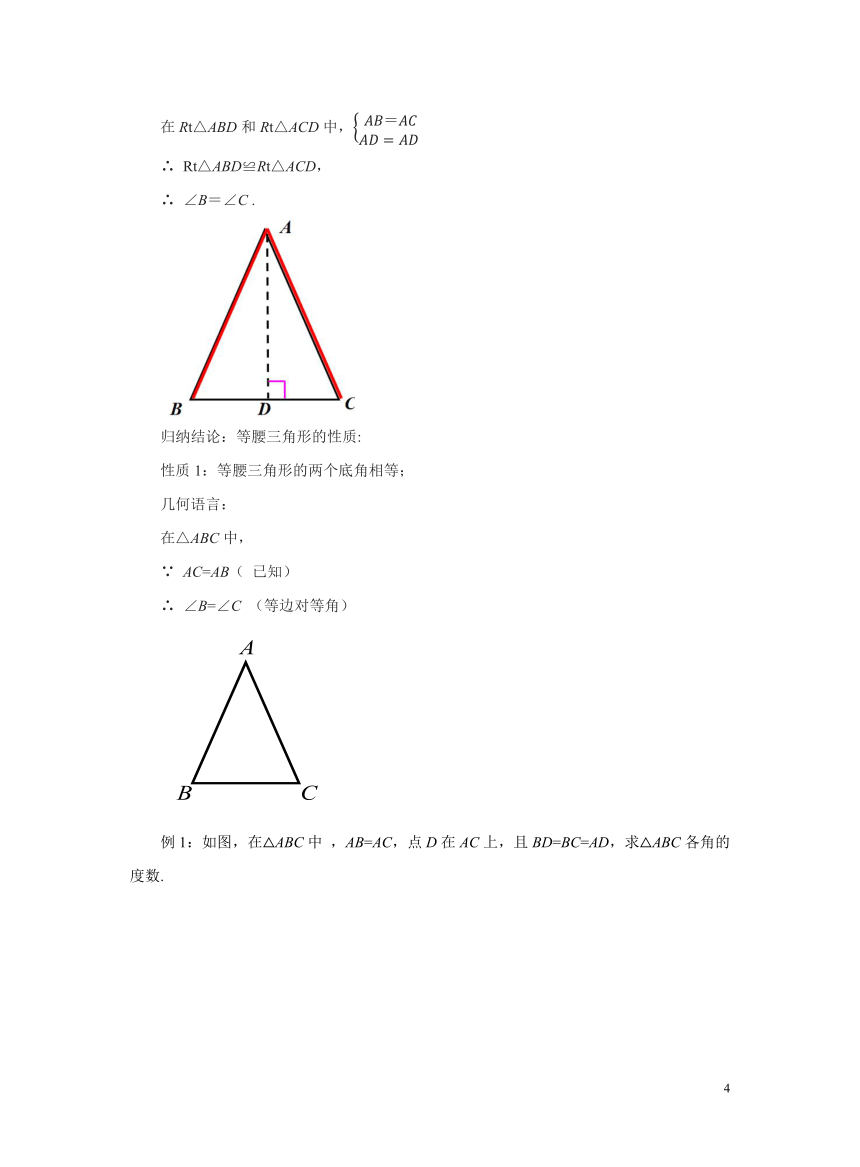
方法三:
证明: 作△ABC 的高线AD,则有 ∠ADB=∠ADC =90 ,
在Rt△ABD和Rt△ACD中,
∴ Rt△ABD≌Rt△ACD,
∴ ∠B=∠C .
归纳结论:等腰三角形的性质:
性质1:等腰三角形的两个底角相等;
几何语言:
在△ABC中,
∵ AC=AB( 已知)
∴ ∠B=∠C (等边对等角)
例1:如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC, ∠A=∠ABD.
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180 ° ,
解得x=36 ° ,在△ABC中, ∠A=36°,∠ABC=∠C=72°.
课堂练习:
⒈等腰三角形一个底角为75°,它的另外两个角为: 75°, 30°.
⒉等腰三角形一个角为70°,它的另外两个角为: 70°,40°或55°,55°.
3.等腰三角形一个角为110°,它的另外两个角为: 35°,35°.
归纳:
在等腰三角形中, ① 顶角+2×底角=180°;② 顶角=180°-2×底角;③ 底角=(180°-顶角)÷2;④0°<顶角<180°;⑤0°<底角<90°.
(二)等腰三角形的性质2
思考: 由△BAD≌ △CAD,除了可以得到∠B= ∠C之外,你还可以得到那些相等的线段和相等的角?
解:∵△BAD≌ △CAD,由全等三角形的性质易得BD=CD,∠ADB=∠ADC,∠BAD=∠CAD.
又∵ ∠ADB+∠ADC=180°,
∴ ∠ADB=∠ADC=90° ,
即AD是等腰△ABC底边BC上的中线、顶角∠BAC的角平分线、底边BC上的高线 .
归纳结论:等腰三角形的性质:
性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
性质2的几何语言:
如图,
在△ABC中,∵AB=AC,∠1=∠2(已知),
∴BD=CD,AD⊥BC(等腰三角形三线合一).
∵AB=AC,BD=CD (已知),
∴∠1=∠2,AD⊥BC(等腰三角形三线合一).
∵AB=AC,AD⊥BC(已知),
∴BD=CD, ∠1=∠2(等腰三角形三线合一).
通过实践探究,小组讨论,把等腰三角形的性质学习变成看的见的动手活动,降低了学习的难度,完成了本课重点知识的学习.
进一步通过作图认识等腰三角形的三线合一的性质:
如图,作等腰三角形一腰上的中线、高和角平分线.
实践发现:三线不合一.
强调:等腰三角形是轴对称图形,只有底边上的中线、高和角平分线才能重合.
课堂练习:
判断对错:
1.等腰三角形的顶角一定是锐角.
2.等腰三角形的底角可能是锐角或者直角、钝角都可以.
3.钝角三角形不可能是等腰三角形.
4.等腰三角形的顶角平分线一定垂直底边.
5.等腰三角形的角平分线、中线和高互相重合.
6.等腰三角形底边上的中线一定平分顶角.
例2:已知点D,E在△ABC的边BC上,AB=AC.
(1)如图①,若AD=AE,求证:BD=CE;
(2)如图②,若BD=CE,F为DE的中点,求证:AF⊥BC.
证明:(1)如图①,过A作AG⊥BC于G.
∵AB=AC,AD=AE,
∴BG=CG,DG=EG,
∴BG-DG=CG-EG,
∴BD=CE;
(2)∵BD=CE,F为DE的中点,
∴BD+DF=CE+EF,
∴BF=CF.
∵AB=AC,∴AF⊥BC.
课堂练习:
1.等腰△ABC中,AB=AC,∠A=30°,则∠B=( )
A.30° B.60° C.75° D.85°
2.等腰三角形的一个外角是100°,它的顶角的度数是( )
A.80° B.20° C.20°或80° D.50°或80°
3.如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=30°求∠1和∠ADC的度数.
解:∵ AB=AC,D是BC边上的中点,
∴∠ADC= 90°,
∵ ∠BAC=180°-30°-30°=120°,
∴∠1=60°.
课堂小结:
说一说等腰三角形的性质.
等边对等角的注意事项:注意是指同一个三角形中.
三线合一的注意事项:指顶角的平分线,底边上的高和中线才有这一性质.而腰上高和中线与底角的平分线不具有这一性质.
作业布置:
1.如图,已知∠A=36°,∠DBC=36°,∠C=72°,则∠DBC=_____,∠BDC=_____,图中的等腰三角形有 .
2.完成本节配套习题.
【板书设计】
等腰三角形的性质:
轴对称图形;等边对等角;三线合一.
等腰三角形的辅助线的做法:底边垂线或底边中线或顶角平分线.
运用分类讨论的思想和一题多解来研究等腰三角形的问题.
【课后反思】
本节课由于采用了直观操作以及讨论交流等教学方法,从而有效地增强了学生的感性认识,提高了学生对新知识的理解与感悟,因而本节课的教学效果较好,学生对所学的新知识掌握较好,达到了教学的目的. 不足之处是少数学生对等腰三角形的“三线合一”性质理解不透彻,还需要在今后的教学和作业中进一步巩固和提高.
1
【教学目标】
1.探索并证明等腰三角形的两个性质,能利用性质证明两个角相等或两条线段相等.
2.结合等腰三角形性质的探索与证明过程,体会轴对称在研究几何问题中的作用,了解作辅助线的技巧,发展“转化”及“分类讨论”的数学思想.
3.引导学生对图形观察、发现,激发学生的求知欲望和学习兴趣,帮助学生养成良好的学习习惯和勤于思考、勇于探索的的思想品质,建立学习的自信心.
【教学重难点】
重点:1.等腰三角形的概念及性质;2.等腰三角形性质的应用.
难点:等腰三角形三线合一的性质的理解及其应用.
【教学方法】
探究实践法、小组合作法、合情推理法.
【教学过程】
新课导入:
创设情境,提出问题:
欣赏下列图片,找出图片中的三角形,观察它们的特点.
观察图片,从生活常见的现象入手,发现特点,进入新课学习.
新课讲授:
(一)等腰三角形的性质1
动手探究:
如图所示,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC 有什么特点?
通过动手体验,小组合作展示探究结论:
所得三角形是等腰三角形,折痕所在直线是对称轴,垂直平分三角形的边,剪痕是三角形相等的两条边.
等腰三角形是轴对称图形.
找一找:把剪出的等腰△ABC沿折痕对折,找出其中重合的线段和角.你能发现等腰三角形的性质吗?
重合线段:AB与AC,BD与CD,AD与AD
重合的边:∠B与∠C,∠BAD与∠CAD,∠ADB与∠ADC.
已知: 如图,在△ABC中,AB=AC.
求证: ∠B=∠C.
证明: 作底边的中线AD, 则BD=CD.
在△BAD和△CAD中,
∴ △BAD≌ △CAD,
∴ ∠B= ∠C.
思考: 还有哪些方法可以得到∠B=∠C?
方法二:
证明: 作顶角的平分线AD,则有∠1=∠2.
在△ABD和△ACD中,
∴ △ABD≌ △ACD ,
∴ ∠B=∠C .
方法三:
证明: 作△ABC 的高线AD,则有 ∠ADB=∠ADC =90 ,
在Rt△ABD和Rt△ACD中,
∴ Rt△ABD≌Rt△ACD,
∴ ∠B=∠C .
归纳结论:等腰三角形的性质:
性质1:等腰三角形的两个底角相等;
几何语言:
在△ABC中,
∵ AC=AB( 已知)
∴ ∠B=∠C (等边对等角)
例1:如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC, ∠A=∠ABD.
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180 ° ,
解得x=36 ° ,在△ABC中, ∠A=36°,∠ABC=∠C=72°.
课堂练习:
⒈等腰三角形一个底角为75°,它的另外两个角为: 75°, 30°.
⒉等腰三角形一个角为70°,它的另外两个角为: 70°,40°或55°,55°.
3.等腰三角形一个角为110°,它的另外两个角为: 35°,35°.
归纳:
在等腰三角形中, ① 顶角+2×底角=180°;② 顶角=180°-2×底角;③ 底角=(180°-顶角)÷2;④0°<顶角<180°;⑤0°<底角<90°.
(二)等腰三角形的性质2
思考: 由△BAD≌ △CAD,除了可以得到∠B= ∠C之外,你还可以得到那些相等的线段和相等的角?
解:∵△BAD≌ △CAD,由全等三角形的性质易得BD=CD,∠ADB=∠ADC,∠BAD=∠CAD.
又∵ ∠ADB+∠ADC=180°,
∴ ∠ADB=∠ADC=90° ,
即AD是等腰△ABC底边BC上的中线、顶角∠BAC的角平分线、底边BC上的高线 .
归纳结论:等腰三角形的性质:
性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
性质2的几何语言:
如图,
在△ABC中,∵AB=AC,∠1=∠2(已知),
∴BD=CD,AD⊥BC(等腰三角形三线合一).
∵AB=AC,BD=CD (已知),
∴∠1=∠2,AD⊥BC(等腰三角形三线合一).
∵AB=AC,AD⊥BC(已知),
∴BD=CD, ∠1=∠2(等腰三角形三线合一).
通过实践探究,小组讨论,把等腰三角形的性质学习变成看的见的动手活动,降低了学习的难度,完成了本课重点知识的学习.
进一步通过作图认识等腰三角形的三线合一的性质:
如图,作等腰三角形一腰上的中线、高和角平分线.
实践发现:三线不合一.
强调:等腰三角形是轴对称图形,只有底边上的中线、高和角平分线才能重合.
课堂练习:
判断对错:
1.等腰三角形的顶角一定是锐角.
2.等腰三角形的底角可能是锐角或者直角、钝角都可以.
3.钝角三角形不可能是等腰三角形.
4.等腰三角形的顶角平分线一定垂直底边.
5.等腰三角形的角平分线、中线和高互相重合.
6.等腰三角形底边上的中线一定平分顶角.
例2:已知点D,E在△ABC的边BC上,AB=AC.
(1)如图①,若AD=AE,求证:BD=CE;
(2)如图②,若BD=CE,F为DE的中点,求证:AF⊥BC.
证明:(1)如图①,过A作AG⊥BC于G.
∵AB=AC,AD=AE,
∴BG=CG,DG=EG,
∴BG-DG=CG-EG,
∴BD=CE;
(2)∵BD=CE,F为DE的中点,
∴BD+DF=CE+EF,
∴BF=CF.
∵AB=AC,∴AF⊥BC.
课堂练习:
1.等腰△ABC中,AB=AC,∠A=30°,则∠B=( )
A.30° B.60° C.75° D.85°
2.等腰三角形的一个外角是100°,它的顶角的度数是( )
A.80° B.20° C.20°或80° D.50°或80°
3.如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=30°求∠1和∠ADC的度数.
解:∵ AB=AC,D是BC边上的中点,
∴∠ADC= 90°,
∵ ∠BAC=180°-30°-30°=120°,
∴∠1=60°.
课堂小结:
说一说等腰三角形的性质.
等边对等角的注意事项:注意是指同一个三角形中.
三线合一的注意事项:指顶角的平分线,底边上的高和中线才有这一性质.而腰上高和中线与底角的平分线不具有这一性质.
作业布置:
1.如图,已知∠A=36°,∠DBC=36°,∠C=72°,则∠DBC=_____,∠BDC=_____,图中的等腰三角形有 .
2.完成本节配套习题.
【板书设计】
等腰三角形的性质:
轴对称图形;等边对等角;三线合一.
等腰三角形的辅助线的做法:底边垂线或底边中线或顶角平分线.
运用分类讨论的思想和一题多解来研究等腰三角形的问题.
【课后反思】
本节课由于采用了直观操作以及讨论交流等教学方法,从而有效地增强了学生的感性认识,提高了学生对新知识的理解与感悟,因而本节课的教学效果较好,学生对所学的新知识掌握较好,达到了教学的目的. 不足之处是少数学生对等腰三角形的“三线合一”性质理解不透彻,还需要在今后的教学和作业中进一步巩固和提高.
1
