初中数学人教版八上13.3.1等腰三角形第2课时 教案
文档属性
| 名称 | 初中数学人教版八上13.3.1等腰三角形第2课时 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 148.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 16:07:12 | ||
图片预览

文档简介
13.3.1等腰三角形(第2课时)
【教学目标】
1. 探索等腰三角形判定定理;理解等腰三角形的判定定理,并会运用其进行简单的证明;了解等腰三角形的尺规作图.
2.通过独立思考,交流讨论,发展推理能力和运用数学知识解决实际问题的能力.
3.学生在探索问题的过程中,体验解决问题的方法和乐趣,增强学习数学的兴趣.
【教学重难点】
重点:理解和运用等腰三角形的判定定理.
难点:利用尺规作等腰三角形:已知底边及底边上的高作等腰三角形.
【教学方法】
探究实践法、小组合作法、合情推理法.
【教学过程】
新课导入:
创设情境,提出问题:
活动探究:
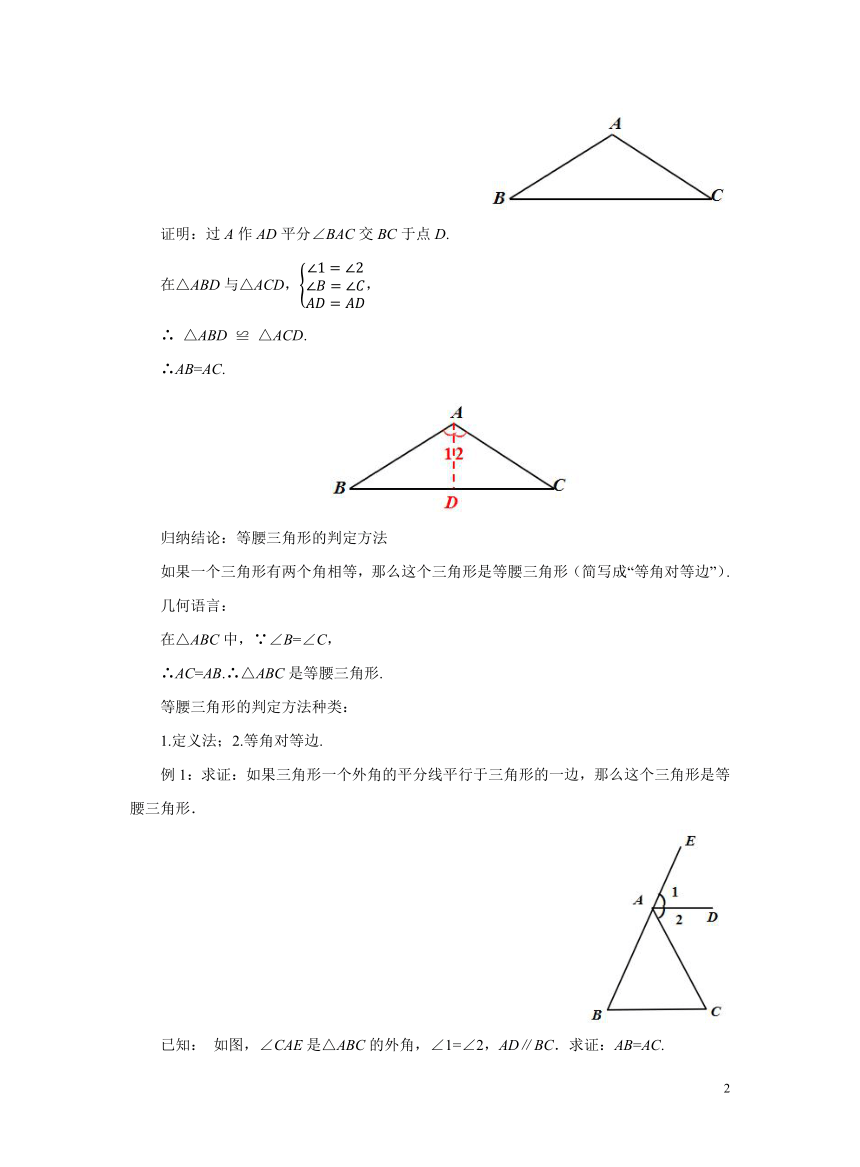
如图,位于海上B、C两处的两艘救生船接到A处遇险船只的报警,当时测得∠B=∠C.如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪因素)?
新课讲授:
等腰三角形的判定
利用几何画板演示实际,观察三角形的边角变化后大胆猜测结论.
从活动中抽象出数学习题:
已知:如图,在△ABC中, ∠B=∠C,那么它们所对的边AB和AC有什么数量关系
证明:过A作AD平分∠BAC交BC于点D.
在△ABD与△ACD,,
∴ △ABD ≌ △ACD.
∴AB=AC.
归纳结论:等腰三角形的判定方法
如果一个三角形有两个角相等,那么这个三角形是等腰三角形(简写成“等角对等边”).
几何语言:
在△ABC中,∵∠B=∠C,
∴AC=AB.∴△ABC是等腰三角形.
等腰三角形的判定方法种类:
1.定义法;2.等角对等边.
例1:求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
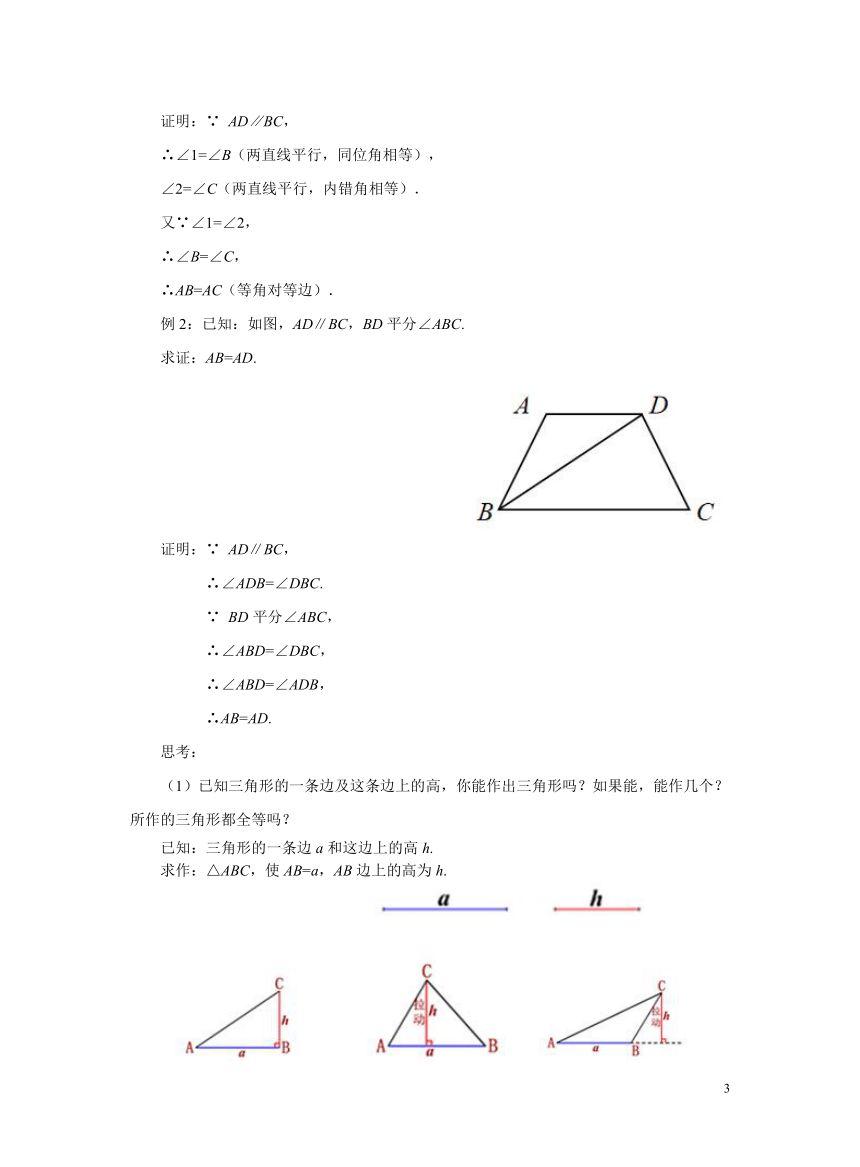
已知: 如图,∠CAE是△ABC的外角,∠1=∠2,AD∥BC.求证:AB=AC.
证明:∵ AD∥BC,
∴∠1=∠B(两直线平行,同位角相等),
∠2=∠C(两直线平行,内错角相等).
又∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等角对等边).
例2:已知:如图,AD∥BC,BD平分∠ABC.
求证:AB=AD.
证明:∵ AD∥BC,
∴∠ADB=∠DBC.
∵ BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD.
思考:
(1)已知三角形的一条边及这条边上的高,你能作出三角形吗?如果能,能作几个?所作的三角形都全等吗?
已知:三角形的一条边a和这边上的高h.
求作:△ABC,使AB=a,AB边上的高为h.
(2)如果已知是等腰三角形的底边及底边上的高,你能用尺规作出等腰三角形吗?能作几个?
例3:已知等腰三角形底边长为a ,底边上的高的长为h ,求作这个等腰三角形.
作法:
(1)作线段AB =a;
(2)作线段AB 的垂直平分线MN,与AB 相交于点D;
(3)在MN上取一点C,使DC =h;
(4)连接AC,BC,则△ABC 就是所求作的等腰三角形.
课堂练习:
如图所示,在△ABC中,已知AB=AC,要使AD = AE,需要添加的一个条件是 __________. (答案不唯一;提示:BE = CD)
2. 已知:如图,AB=DC,BD=CA,BD与CA相交于点E.求证:△AED是等腰三角形.
证明:∵AB=DC,BD=CA,AD=DA,
∴△ABD≌△DCA(SSS),
∴∠ADB=∠DAC(全等三角形的对应角相等),
∴AE=DE(等角对等边),
∴ △AED是等腰三角形.
3.如图,把一张长方形的纸沿着对角线折叠,重合部分是一个等腰三角形吗?为什么?
解:是等腰三角形.理由如下:
∵ △ABD≌ △CDB,
∴∠ADB=∠CBD,
∴ △EBD是等腰三角形.
课堂小结:
提出问题:问1:通过这节课的学习,你收获了几种等腰三角形的判定方法?
问2:如何区分等腰三角形的性质和判定?
问3:证明线段相等的方法有哪些?
等边对等角的注意事项:注意是指同一个三角形中.
三线合一的注意事项:指顶角的平分线,底边上的高和中线才有这一性质.而腰上高和中线与底角的平分线不具有这一性质.
作业布置:
1.如图,已知∠A=36°,∠DBC=36°,∠C=72°,则∠DBC=_____,∠BDC=_____,图中的等腰三角形有____________.
2.完成本节配套习题.
【板书设计】
等腰三角形的性质:
等边对等角;三线合一.
等腰三角形的判定:
定义;等角对等边.
【课后反思】
将本节课的教学目标展示给学生,让学生做到心中有数,让学生带着问题观察几何画板演示的三角形的边角变化,加强自主探索的能力. 通过学生观察、思考例题,自然地渗透分类讨论的数学解题思想. 通过课堂小结,让学生归纳比较等腰三角形的性质和判定的区别,同时将等腰三角形的性质定理与判定定理有机的结合起来,重在培养学生对两个知识点的综合运用,鼓励学生积极思考.
1
【教学目标】
1. 探索等腰三角形判定定理;理解等腰三角形的判定定理,并会运用其进行简单的证明;了解等腰三角形的尺规作图.
2.通过独立思考,交流讨论,发展推理能力和运用数学知识解决实际问题的能力.
3.学生在探索问题的过程中,体验解决问题的方法和乐趣,增强学习数学的兴趣.
【教学重难点】
重点:理解和运用等腰三角形的判定定理.
难点:利用尺规作等腰三角形:已知底边及底边上的高作等腰三角形.
【教学方法】
探究实践法、小组合作法、合情推理法.
【教学过程】
新课导入:
创设情境,提出问题:
活动探究:
如图,位于海上B、C两处的两艘救生船接到A处遇险船只的报警,当时测得∠B=∠C.如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪因素)?
新课讲授:
等腰三角形的判定
利用几何画板演示实际,观察三角形的边角变化后大胆猜测结论.
从活动中抽象出数学习题:
已知:如图,在△ABC中, ∠B=∠C,那么它们所对的边AB和AC有什么数量关系
证明:过A作AD平分∠BAC交BC于点D.
在△ABD与△ACD,,
∴ △ABD ≌ △ACD.
∴AB=AC.
归纳结论:等腰三角形的判定方法
如果一个三角形有两个角相等,那么这个三角形是等腰三角形(简写成“等角对等边”).
几何语言:
在△ABC中,∵∠B=∠C,
∴AC=AB.∴△ABC是等腰三角形.
等腰三角形的判定方法种类:
1.定义法;2.等角对等边.
例1:求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知: 如图,∠CAE是△ABC的外角,∠1=∠2,AD∥BC.求证:AB=AC.
证明:∵ AD∥BC,
∴∠1=∠B(两直线平行,同位角相等),
∠2=∠C(两直线平行,内错角相等).
又∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等角对等边).
例2:已知:如图,AD∥BC,BD平分∠ABC.
求证:AB=AD.
证明:∵ AD∥BC,
∴∠ADB=∠DBC.
∵ BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD.
思考:
(1)已知三角形的一条边及这条边上的高,你能作出三角形吗?如果能,能作几个?所作的三角形都全等吗?
已知:三角形的一条边a和这边上的高h.
求作:△ABC,使AB=a,AB边上的高为h.
(2)如果已知是等腰三角形的底边及底边上的高,你能用尺规作出等腰三角形吗?能作几个?
例3:已知等腰三角形底边长为a ,底边上的高的长为h ,求作这个等腰三角形.
作法:
(1)作线段AB =a;
(2)作线段AB 的垂直平分线MN,与AB 相交于点D;
(3)在MN上取一点C,使DC =h;
(4)连接AC,BC,则△ABC 就是所求作的等腰三角形.
课堂练习:
如图所示,在△ABC中,已知AB=AC,要使AD = AE,需要添加的一个条件是 __________. (答案不唯一;提示:BE = CD)
2. 已知:如图,AB=DC,BD=CA,BD与CA相交于点E.求证:△AED是等腰三角形.
证明:∵AB=DC,BD=CA,AD=DA,
∴△ABD≌△DCA(SSS),
∴∠ADB=∠DAC(全等三角形的对应角相等),
∴AE=DE(等角对等边),
∴ △AED是等腰三角形.
3.如图,把一张长方形的纸沿着对角线折叠,重合部分是一个等腰三角形吗?为什么?
解:是等腰三角形.理由如下:
∵ △ABD≌ △CDB,
∴∠ADB=∠CBD,
∴ △EBD是等腰三角形.
课堂小结:
提出问题:问1:通过这节课的学习,你收获了几种等腰三角形的判定方法?
问2:如何区分等腰三角形的性质和判定?
问3:证明线段相等的方法有哪些?
等边对等角的注意事项:注意是指同一个三角形中.
三线合一的注意事项:指顶角的平分线,底边上的高和中线才有这一性质.而腰上高和中线与底角的平分线不具有这一性质.
作业布置:
1.如图,已知∠A=36°,∠DBC=36°,∠C=72°,则∠DBC=_____,∠BDC=_____,图中的等腰三角形有____________.
2.完成本节配套习题.
【板书设计】
等腰三角形的性质:
等边对等角;三线合一.
等腰三角形的判定:
定义;等角对等边.
【课后反思】
将本节课的教学目标展示给学生,让学生做到心中有数,让学生带着问题观察几何画板演示的三角形的边角变化,加强自主探索的能力. 通过学生观察、思考例题,自然地渗透分类讨论的数学解题思想. 通过课堂小结,让学生归纳比较等腰三角形的性质和判定的区别,同时将等腰三角形的性质定理与判定定理有机的结合起来,重在培养学生对两个知识点的综合运用,鼓励学生积极思考.
1
