初中数学人教版八上13.3.1等腰三角形第2课时 习题(含答案)
文档属性
| 名称 | 初中数学人教版八上13.3.1等腰三角形第2课时 习题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 202.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 13:13:32 | ||
图片预览




文档简介
13.3.1等腰三角形(第2课时)
1. 如图,在△ABC中,, AB=5,则AC的长为( )
A.2 B.3 C.4 D.5
2. 已知:如图,经过线段一端点A有一直线l,直线上l存在点C,使为等腰三角形,这样的点C有( )个.
A.2 B.3 C.4 D.5
3. 下列给出的5个图中,能判定是等腰三角形的有()
A.2个 B.3个 C.4个 D.5个
4. 如图,直线l分别与直线AB、CD相交于点E、F,EG平分∠BEF交直线CD于点G,若∠1=∠BEF,若EF=3,则FG为( )
A.4 B.3 C.5 D.1.5
5. 如图,在中,//,和的平分线分别交于点、,若,,则的值为()
A.3 B.4 C.5 D.9
6.如图,有一种电子游戏,其规则为:电子屏幕上有一正方形,点P沿直线从右往左移动,当出现点P与正方形四个顶点中的两个顶点构成等腰三角形时,就会发出警报,则直线上会发出警报的点P有( )
A.7个 B.8个 C.9个 D.10个
7.如图,△ABC中,BE是角平分线,DE∥BC交AB于D,交AC于E,若DE=9,AD=5,则AB等于( )
A.12 B.13 C.14 D.15
8. 如图,已知△ABC的角平分线CD交AB于D,DE∥BC交AC于E,若DE=3,AE=4,则AC=________.
9. 如图,在等腰△ABC中,BD为∠ABC的平分线,∠A=36°,AB=AC=a,BC=b,则CD= .
10.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于C,若EC=1,则OF=_____.
11.(1)如图1,在△ABC中,∠C=90°,请用直尺和圆规作一条直线,把△ABC分割成两个等腰三角形(不写作法,保留作图痕迹).
(2)已知内角度数的两个三角形,如图2,图3,请你判断,能否分别画一条直线把它们分割成两个等腰三角形?若能,请写出分割成的两个等腰三角形顶角的度数.
12.已知:如图,AC和BD交点O,AB∥CD,OA=OB,求证:OC=OD.
13.如图,∠CAD是△ABC的外角,AE平分∠DAC,AE∥BC,求证:AB=AC.
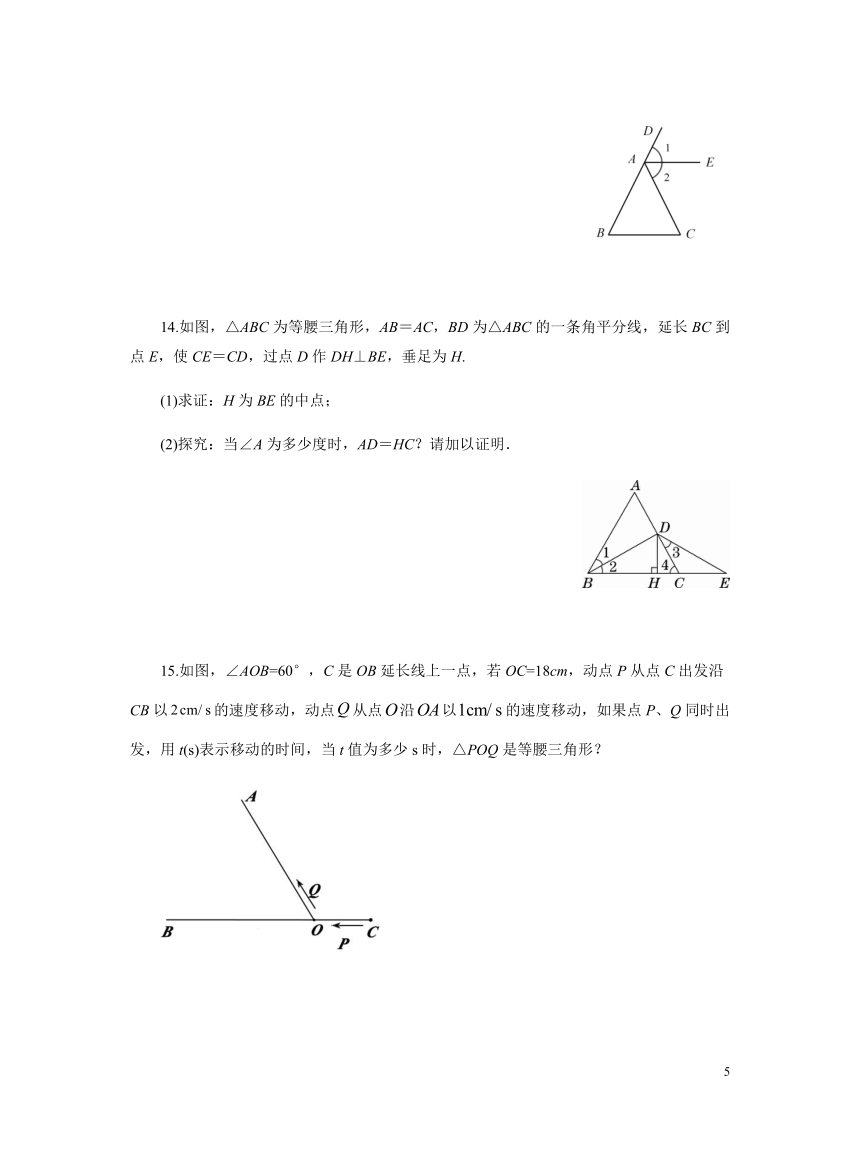
14.如图,△ABC为等腰三角形,AB=AC,BD为△ABC的一条角平分线,延长BC到点E,使CE=CD,过点D作DH⊥BE,垂足为H.
(1)求证:H为BE的中点;
(2)探究:当∠A为多少度时,AD=HC?请加以证明.
15.如图,∠AOB=60°,C是OB延长线上一点,若OC=18cm,动点P从点C出发沿CB以的速度移动,动点从点沿以的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t值为多少s时,△POQ是等腰三角形?
参考答案
1.D
解析:∵,∴AC=AB=5.
2. C
解:如图所示,以B为圆心,以AB的长为半径画弧与直线l交于点D,此时AB=BD,同理以A为圆心以AB的长为半径与直线l交于E、C,此时AC=AB,AE=AB,再作AB的垂直平分线与直线l交于点F,此时AF=BF,
∴一共有4个点满足题意,
3.C
①∠C=180 -∠A-∠B=180 -70 -56 =54 ,∠B=56 ,∠C≠∠B,不是等腰三角形,
②∠C=∠140 -∠B=70 =∠B,是等腰三角形,
③∵AD∥BC,∴∠C=∠DAC=50 ,∠C=∠B=50 ,△ABC是等腰三角形,
④∵AD∥BC,∴∠ABC+∠BAD=180 ,∵∠ABC=120 ,∴∠BAD=60 ,∵∠CAD=30 ,∠CAB=60 -∠CAD=60 -30 =30 ,∵AD∥BC,∴∠BCA=∠CAD=30 ,∴∠BCA=∠CAB=30 ,∴△ABC是等腰三角形,
⑤∵AB∥DE ,∴∠D=∠A=30 ,∵∠DCB=∠A+∠B,∴∠B=∠DCB-∠A=60 -30 =30 , △ABC是等腰三角形.
4.B
解:∵∠1=∠BEF,
∴CD∥AB,
∴∠FGE=∠BEG,
∵EG平分∠BEF,
∴∠FEG=∠BEG,
∴∠FGE=∠FEG,
∴FG=EF=3.
5. 解:∵ED∥BC,
∴∠DFB=∠FBC,∠EGC=∠GCB,
∵∠DBF=∠FBC,∠ECG=∠GCB,
∴∠DFB=∠DBF,∠ECG=∠EGC,
∴BD=DF,CE=GE,
∵FG=2,ED=6,
∴DB+EC=DF+GE=ED FG=6 2=4.
6.C
解析:解:当BC=BP时,△ BCP为等腰三角形;
当P与B重合时,△APC为等腰三角形;
当P运动到AB边的中点时,PD=PC,此时△PCD为等腰三角形;
当P与A重合时,△PBD为等腰三角形;
当PA=AD时,△PAD为等腰三角形;
当AP=AC时,△APC是等腰三角形,这时有2个;
当BD=BP时,△BDP 是等腰三角形,这时有2个;
综上,直线AB上会发出警报的点P有9个.
7.C
解析:∵BE是∠ABC的平分线,∴∠ABE=∠CBE,
∵DE∥BC,∴∠DEB=∠CBE,∴∠ABE=∠DEB,∴BD=DE=9,
∵AB=AD+BD,∴AB=5+9=14.
8.7
解析:∵△ABC的角平分线CD交AB于D,∴∠DEC=∠BCD,
∵DE∥BC,∴∠EDC=∠BCD,
∴∠EDC=∠ECD,
∴DE=CE,
∴AC=DE+CE=3+4=7.
9.(0,4)或(0,-4)或(8,0)或(-4,0)
解析:分别以点A,点O为圆心,4为半径作圆,与坐标轴的交点即为所求.
10.2
解:作EH⊥OA于H.
∵∠AOE=∠BOE=15°,EC⊥OB,EH⊥OA,∴EH=EC=1,∠AOB=30°.
∵EF∥OB,∴∠EFH=∠AOB=30°,∠FEO=∠BOE,
∴EF=2EH=2,∠FEO=∠FOE,∴OF=EF=2.
11.(1)解:如图1,直线CD即为所求.
(2)解:图②能画一条直线将原三角形分割成两个等腰三角形.如图2,分割成的两个等腰三角形的顶角度数分别是132°和84°.图③不能分割成两个等腰三角形.
12.证明:∵OA=OB,∴∠A=∠B,
∵AB∥CD,∴∠A=∠C,∠B=∠D,
∴∠C=∠D,
∴OC=OD.
13. 证明:∵AE∥BC,∴∠1=∠B,∠2=∠C,
∵AE平分∠DAC,∴∠1=∠2,
∴∠B=∠C,∴AB=AC.
14.(1)证明:∵AB=AC,∴∠ABC=∠4.∵BD平分∠ABC,
∴∠1=∠2.∵CE=CD,∴∠3=∠E.∵∠4=∠3+∠E,
∠ABC=∠1+∠2,∴∠2=∠E.
∴BD=ED,即△BDE为等腰三角形.
∵DH⊥BE,∴H为BE的中点(三线合一).
(2)解:当∠A=90°时,AD=HC.证明如下:
∵BD为△ABC的一条角平分线,DH⊥BE,∠A=90°,
∴AD=DH.∵AB=AC,∴△ABC为等腰直角三角形,
∴∠4=45°.∵∠DHC=90°,∴△DHC为等腰直角三角形.
∴DH=HC.∴AD=HC.
15.解:由题意,分以下两种情况:
(1)点P在线段OC上时,若ΔPOQ是等腰三角形,则只有OP=OQ才满足,
因此有18 2t=t,
解得t=6(s).
(2)点P在线段OB上时,若ΔPOQ是等腰三角形,
∵,
∴ΔPOQ也是等边三角形,
因此有2t 18=t,
解得t=18(s) ,
综上,当t等于6s或18s时,ΔPOQ是等腰三角形.
1
1. 如图,在△ABC中,, AB=5,则AC的长为( )
A.2 B.3 C.4 D.5
2. 已知:如图,经过线段一端点A有一直线l,直线上l存在点C,使为等腰三角形,这样的点C有( )个.
A.2 B.3 C.4 D.5
3. 下列给出的5个图中,能判定是等腰三角形的有()
A.2个 B.3个 C.4个 D.5个
4. 如图,直线l分别与直线AB、CD相交于点E、F,EG平分∠BEF交直线CD于点G,若∠1=∠BEF,若EF=3,则FG为( )
A.4 B.3 C.5 D.1.5
5. 如图,在中,//,和的平分线分别交于点、,若,,则的值为()
A.3 B.4 C.5 D.9
6.如图,有一种电子游戏,其规则为:电子屏幕上有一正方形,点P沿直线从右往左移动,当出现点P与正方形四个顶点中的两个顶点构成等腰三角形时,就会发出警报,则直线上会发出警报的点P有( )
A.7个 B.8个 C.9个 D.10个
7.如图,△ABC中,BE是角平分线,DE∥BC交AB于D,交AC于E,若DE=9,AD=5,则AB等于( )
A.12 B.13 C.14 D.15
8. 如图,已知△ABC的角平分线CD交AB于D,DE∥BC交AC于E,若DE=3,AE=4,则AC=________.
9. 如图,在等腰△ABC中,BD为∠ABC的平分线,∠A=36°,AB=AC=a,BC=b,则CD= .
10.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于C,若EC=1,则OF=_____.
11.(1)如图1,在△ABC中,∠C=90°,请用直尺和圆规作一条直线,把△ABC分割成两个等腰三角形(不写作法,保留作图痕迹).
(2)已知内角度数的两个三角形,如图2,图3,请你判断,能否分别画一条直线把它们分割成两个等腰三角形?若能,请写出分割成的两个等腰三角形顶角的度数.
12.已知:如图,AC和BD交点O,AB∥CD,OA=OB,求证:OC=OD.
13.如图,∠CAD是△ABC的外角,AE平分∠DAC,AE∥BC,求证:AB=AC.
14.如图,△ABC为等腰三角形,AB=AC,BD为△ABC的一条角平分线,延长BC到点E,使CE=CD,过点D作DH⊥BE,垂足为H.
(1)求证:H为BE的中点;
(2)探究:当∠A为多少度时,AD=HC?请加以证明.
15.如图,∠AOB=60°,C是OB延长线上一点,若OC=18cm,动点P从点C出发沿CB以的速度移动,动点从点沿以的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t值为多少s时,△POQ是等腰三角形?
参考答案
1.D
解析:∵,∴AC=AB=5.
2. C
解:如图所示,以B为圆心,以AB的长为半径画弧与直线l交于点D,此时AB=BD,同理以A为圆心以AB的长为半径与直线l交于E、C,此时AC=AB,AE=AB,再作AB的垂直平分线与直线l交于点F,此时AF=BF,
∴一共有4个点满足题意,
3.C
①∠C=180 -∠A-∠B=180 -70 -56 =54 ,∠B=56 ,∠C≠∠B,不是等腰三角形,
②∠C=∠140 -∠B=70 =∠B,是等腰三角形,
③∵AD∥BC,∴∠C=∠DAC=50 ,∠C=∠B=50 ,△ABC是等腰三角形,
④∵AD∥BC,∴∠ABC+∠BAD=180 ,∵∠ABC=120 ,∴∠BAD=60 ,∵∠CAD=30 ,∠CAB=60 -∠CAD=60 -30 =30 ,∵AD∥BC,∴∠BCA=∠CAD=30 ,∴∠BCA=∠CAB=30 ,∴△ABC是等腰三角形,
⑤∵AB∥DE ,∴∠D=∠A=30 ,∵∠DCB=∠A+∠B,∴∠B=∠DCB-∠A=60 -30 =30 , △ABC是等腰三角形.
4.B
解:∵∠1=∠BEF,
∴CD∥AB,
∴∠FGE=∠BEG,
∵EG平分∠BEF,
∴∠FEG=∠BEG,
∴∠FGE=∠FEG,
∴FG=EF=3.
5. 解:∵ED∥BC,
∴∠DFB=∠FBC,∠EGC=∠GCB,
∵∠DBF=∠FBC,∠ECG=∠GCB,
∴∠DFB=∠DBF,∠ECG=∠EGC,
∴BD=DF,CE=GE,
∵FG=2,ED=6,
∴DB+EC=DF+GE=ED FG=6 2=4.
6.C
解析:解:当BC=BP时,△ BCP为等腰三角形;
当P与B重合时,△APC为等腰三角形;
当P运动到AB边的中点时,PD=PC,此时△PCD为等腰三角形;
当P与A重合时,△PBD为等腰三角形;
当PA=AD时,△PAD为等腰三角形;
当AP=AC时,△APC是等腰三角形,这时有2个;
当BD=BP时,△BDP 是等腰三角形,这时有2个;
综上,直线AB上会发出警报的点P有9个.
7.C
解析:∵BE是∠ABC的平分线,∴∠ABE=∠CBE,
∵DE∥BC,∴∠DEB=∠CBE,∴∠ABE=∠DEB,∴BD=DE=9,
∵AB=AD+BD,∴AB=5+9=14.
8.7
解析:∵△ABC的角平分线CD交AB于D,∴∠DEC=∠BCD,
∵DE∥BC,∴∠EDC=∠BCD,
∴∠EDC=∠ECD,
∴DE=CE,
∴AC=DE+CE=3+4=7.
9.(0,4)或(0,-4)或(8,0)或(-4,0)
解析:分别以点A,点O为圆心,4为半径作圆,与坐标轴的交点即为所求.
10.2
解:作EH⊥OA于H.
∵∠AOE=∠BOE=15°,EC⊥OB,EH⊥OA,∴EH=EC=1,∠AOB=30°.
∵EF∥OB,∴∠EFH=∠AOB=30°,∠FEO=∠BOE,
∴EF=2EH=2,∠FEO=∠FOE,∴OF=EF=2.
11.(1)解:如图1,直线CD即为所求.
(2)解:图②能画一条直线将原三角形分割成两个等腰三角形.如图2,分割成的两个等腰三角形的顶角度数分别是132°和84°.图③不能分割成两个等腰三角形.
12.证明:∵OA=OB,∴∠A=∠B,
∵AB∥CD,∴∠A=∠C,∠B=∠D,
∴∠C=∠D,
∴OC=OD.
13. 证明:∵AE∥BC,∴∠1=∠B,∠2=∠C,
∵AE平分∠DAC,∴∠1=∠2,
∴∠B=∠C,∴AB=AC.
14.(1)证明:∵AB=AC,∴∠ABC=∠4.∵BD平分∠ABC,
∴∠1=∠2.∵CE=CD,∴∠3=∠E.∵∠4=∠3+∠E,
∠ABC=∠1+∠2,∴∠2=∠E.
∴BD=ED,即△BDE为等腰三角形.
∵DH⊥BE,∴H为BE的中点(三线合一).
(2)解:当∠A=90°时,AD=HC.证明如下:
∵BD为△ABC的一条角平分线,DH⊥BE,∠A=90°,
∴AD=DH.∵AB=AC,∴△ABC为等腰直角三角形,
∴∠4=45°.∵∠DHC=90°,∴△DHC为等腰直角三角形.
∴DH=HC.∴AD=HC.
15.解:由题意,分以下两种情况:
(1)点P在线段OC上时,若ΔPOQ是等腰三角形,则只有OP=OQ才满足,
因此有18 2t=t,
解得t=6(s).
(2)点P在线段OB上时,若ΔPOQ是等腰三角形,
∵,
∴ΔPOQ也是等边三角形,
因此有2t 18=t,
解得t=18(s) ,
综上,当t等于6s或18s时,ΔPOQ是等腰三角形.
1
