初中数学人教版八上13.3.2等边三角形第1课时 教案
文档属性
| 名称 | 初中数学人教版八上13.3.2等边三角形第1课时 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 121.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 16:07:58 | ||
图片预览


文档简介
13.3.2等边三角形(第1课时)
【教学目标】
1.探索等边三角形的性质和判定;能运用等边三角形的性质和判定进行计算和证明.
2.通过探索、猜想、证明、归纳等数学活动过程,发展逻辑推理能力.
3.体验解决问题的方法和乐趣,增强学习兴趣.
【教学重难点】
重点:探索等边三角形的性质与判定.
难点:等边三角形性质和判定的应用.
【教学方法】
探究实践法、类比法、合情推理法.
【教学过程】
新课导入:
提出问题:同学们知道的等腰三角形的性质和判定有哪些内容?
性质:等腰三角形的两个底角相等.
等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合.
判定:如果一个三角形有两个角相等,那么这个三角形是等腰三角形.
请分别画出一个等腰三角形和等边三角形,结合你画的图形说出它们有什么区别和联系?
分小组展示结论.
联系:等边三角形是特殊的等腰三角形;
区别:等边三角形有三条相等的边,而等腰三角形只有两条.
新课讲授:
(一)等边三角形的性质
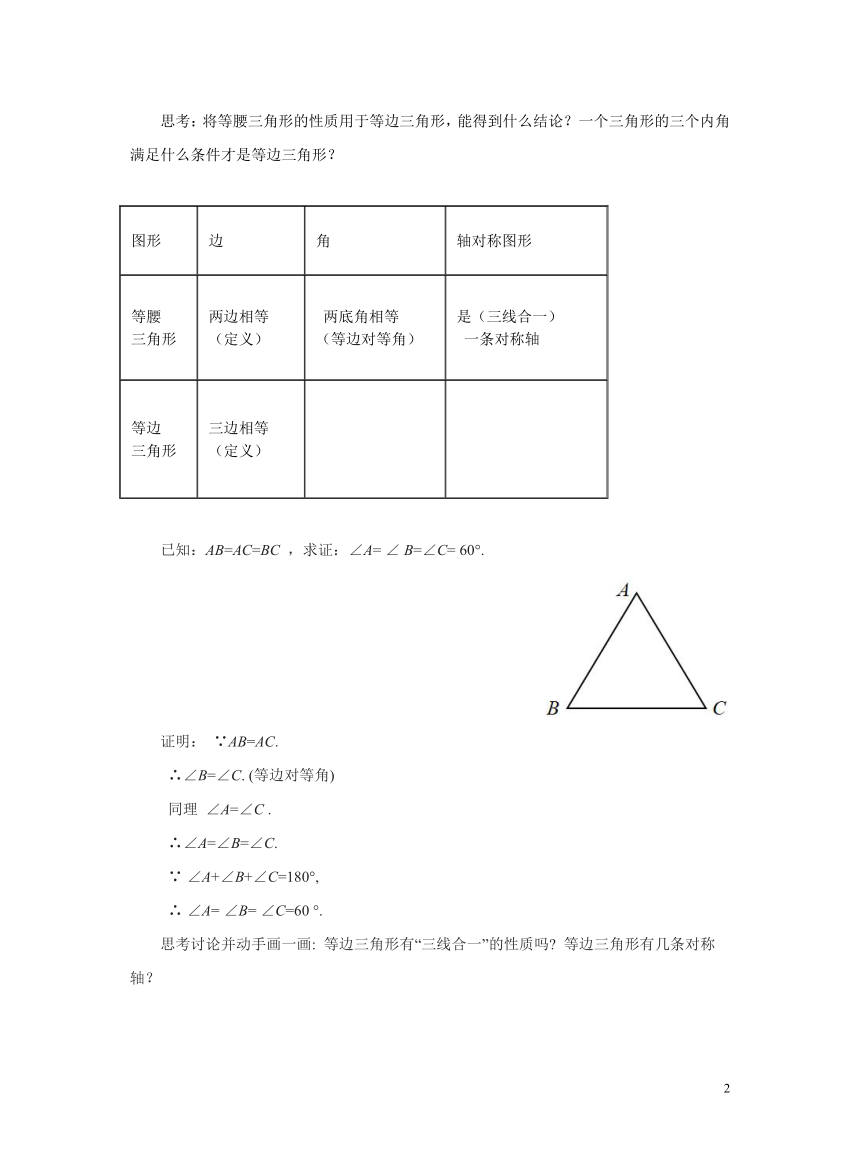
思考:将等腰三角形的性质用于等边三角形,能得到什么结论?一个三角形的三个内角满足什么条件才是等边三角形?
图形 边 角 轴对称图形
等腰 三角形 两边相等 (定义) 两底角相等 (等边对等角) 是(三线合一) 一条对称轴
等边 三角形 三边相等 (定义)
已知:AB=AC=BC ,求证:∠A= ∠ B=∠C= 60°.
证明: ∵AB=AC.
∴∠B=∠C. (等边对等角)
同理 ∠A=∠C .
∴∠A=∠B=∠C.
∵ ∠A+∠B+∠C=180°,
∴ ∠A= ∠B= ∠C=60 °.
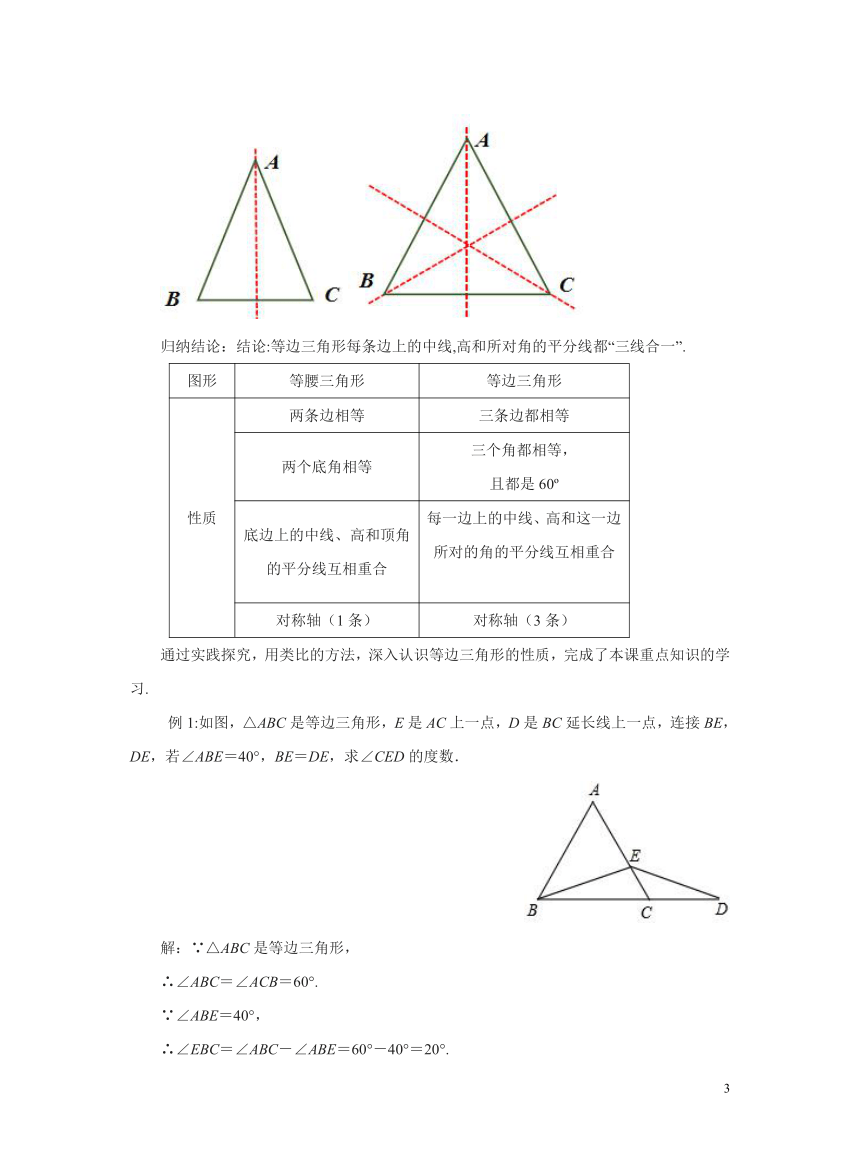
思考讨论并动手画一画: 等边三角形有“三线合一”的性质吗 等边三角形有几条对称轴?
归纳结论:结论:等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.
图形 等腰三角形 等边三角形
性质 两条边相等 三条边都相等
两个底角相等 三个角都相等, 且都是60
底边上的中线、高和顶角的平分线互相重合 每一边上的中线、高和这一边所对的角的平分线互相重合
对称轴(1条) 对称轴(3条)
通过实践探究,用类比的方法,深入认识等边三角形的性质,完成了本课重点知识的学习.
例1:如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数.
解:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵∠ABE=40°,
∴∠EBC=∠ABC-∠ABE=60°-40°=20°.
∵BE=DE,
∴∠D=∠EBC=20°,
∴∠CED=∠ACB-∠D=40°.
课堂练习:
变式:如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.求证:BD=DE.
证明:∵△ABC是等边三角形,BD是角平分线,
∴∠ABC=∠ACB=60°,∠DBC=30°.
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=30°.
∴∠DBC=∠DEC.
∴DB=DE(等角对等边).
例2: △ABC为正三角形,点M是BC边上任意一点,点N是CA边上任意一点,且BM=CN,BN与AM相交于Q点,∠BQM等于多少度?
解:∵△ABC为正三角形,
∴∠ABC=∠C=∠BAC=60°,AB=BC.
又∵BM=CN,
∴△AMB≌△BNC(SAS),
∴∠BAM=∠CBN,
∴∠BQM=∠ABQ+∠BAM
=∠ABQ+∠CBN=∠ABC=60°.
(二)等边三角形的判定
图形 等腰三角形 等边三角形
判定 从边看:两条边相等的三角形是等腰三角形 三条边都相等的三角形是等边三角形
从角看:两个角相等的三角形是等腰三角形 三个角都相等的三角形是等边三角形
等边三角形的判定方法:
有一个角是60°的等腰三角形是等边三角形.
用类比的方法从等腰三角形的判定方法分析得出等边三角形的判定方法,水到渠成,容易接受.
例2:如图,△ABC 是等边三角形,DE∥BC,分别交AB,AC 于点D,E.求证:△ADE 是等边三角形.
证明: ∵△ABC 是等边三角形,
∴∠A =∠B =∠C =60°.
∵DE∥BC,
∴∠B =∠ADE,∠C =∠AED.
∴∠A=∠ADE =∠AED.
∴△ADE 是等边三角形.
变式1:若点D、E 在边AB、AC 的延长线上,且DE∥BC,结论还成立吗?
证明:∵△ABC 是等边三角形,
∴∠A =∠ABC =∠ACB =60°.
∵DE∥BC,
∴∠ABC =∠ADE,∠ACB =∠AED.
∴∠A =∠ADE =∠AED.
∴△ADE 是等边三角形.
变式2:若点D、E 在边AB、AC 的反向延长线上,且DE∥BC,结论依然成立吗?
证明: ∵ △ABC 是等边三角形,
∴∠BAC =∠B =∠C =60°.
∵DE∥BC,
∴∠B =∠D,∠C =∠E.
∴∠EAD =∠D =∠E.
∴△ADE 是等边三角形.
变式3:上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗 试说明理由.
证明:∵ △ABC是等边三角形,
∴ ∠A=∠B=∠C.
∵ AD=AE,
∴ ∠ADE=∠B, ∠AED=∠C.
∴ ∠A=∠ADE= ∠AED.
∴ △ADE是等边三角形.
课堂练习:
1. 以下叙述中不正确的是( C )
A.等边三角形的每条高线都是角平分线和中线
B.其中有一内角为60°的等腰三角形是等边三角形
C.等腰三角形一定是锐角三角形
D.在一个三角形中,如果两条边不相等,那么它们所对的角也不相等;反之,在一个三角形中,如果两个角不相等,那么它们所对的边也不相等.
2. 已知等边三角形ABC的边长为6,D是AB上的动点,过点D作DE⊥AC于点E,过点E作EF⊥BC于点F,过点F作FG⊥AB于点G,当点G与点D重合时,AD的长为( )
A.4 B.6 C.8 D.9
3.如图,等边△ABC中,D、E、F分别是各边上的一点,且AD=BE=CF.
求证:△DEF是等边三角形.
证明:∵△ABC为等边三角形,且AD=BE=CF
∴AF=BD=CE,∠A=∠B=∠C=60°,
∴△ADF≌△BED≌△CFE(SAS),
∴DF=ED=EF,
∴△DEF是等边三角形.
课堂小结:
对比等腰三角形的性质与判定方法,说一说等边三角形的性质与判定方法.
注意等边三角形判定方法的特殊性:三边法、三角法、等腰三角形法.
作业布置:
1.等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试证明你的结论.
解:△APQ为等边三角形.
证明如下:∵△ABC为等边三角形,
∴AB=AC.
∵BP=CQ,∠ABP=∠ACQ,
∴△ABP≌△ACQ(SAS),
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
2.完成本节配套习题.
【板书设计】
等边三角形的定义,等腰三角形的底等腰;
等边三角形的性质:边、角、轴对称性;
等边三角形的判定方法:三边法、三角法、等腰三角形法.
【课后反思】
学习特殊的等腰三角形——等边三角形,让学生先通过画图,比较等方法自主探索,小组内、小组间充分交流后概括所得结论,这既巩固等腰三角形的应用知识,又类比探索等腰三角形性质和判定定理的方法,加深了对等腰三角形与等边三角形联系与区别的理解.
1
【教学目标】
1.探索等边三角形的性质和判定;能运用等边三角形的性质和判定进行计算和证明.
2.通过探索、猜想、证明、归纳等数学活动过程,发展逻辑推理能力.
3.体验解决问题的方法和乐趣,增强学习兴趣.
【教学重难点】
重点:探索等边三角形的性质与判定.
难点:等边三角形性质和判定的应用.
【教学方法】
探究实践法、类比法、合情推理法.
【教学过程】
新课导入:
提出问题:同学们知道的等腰三角形的性质和判定有哪些内容?
性质:等腰三角形的两个底角相等.
等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合.
判定:如果一个三角形有两个角相等,那么这个三角形是等腰三角形.
请分别画出一个等腰三角形和等边三角形,结合你画的图形说出它们有什么区别和联系?
分小组展示结论.
联系:等边三角形是特殊的等腰三角形;
区别:等边三角形有三条相等的边,而等腰三角形只有两条.
新课讲授:
(一)等边三角形的性质
思考:将等腰三角形的性质用于等边三角形,能得到什么结论?一个三角形的三个内角满足什么条件才是等边三角形?
图形 边 角 轴对称图形
等腰 三角形 两边相等 (定义) 两底角相等 (等边对等角) 是(三线合一) 一条对称轴
等边 三角形 三边相等 (定义)
已知:AB=AC=BC ,求证:∠A= ∠ B=∠C= 60°.
证明: ∵AB=AC.
∴∠B=∠C. (等边对等角)
同理 ∠A=∠C .
∴∠A=∠B=∠C.
∵ ∠A+∠B+∠C=180°,
∴ ∠A= ∠B= ∠C=60 °.
思考讨论并动手画一画: 等边三角形有“三线合一”的性质吗 等边三角形有几条对称轴?
归纳结论:结论:等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.
图形 等腰三角形 等边三角形
性质 两条边相等 三条边都相等
两个底角相等 三个角都相等, 且都是60
底边上的中线、高和顶角的平分线互相重合 每一边上的中线、高和这一边所对的角的平分线互相重合
对称轴(1条) 对称轴(3条)
通过实践探究,用类比的方法,深入认识等边三角形的性质,完成了本课重点知识的学习.
例1:如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数.
解:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵∠ABE=40°,
∴∠EBC=∠ABC-∠ABE=60°-40°=20°.
∵BE=DE,
∴∠D=∠EBC=20°,
∴∠CED=∠ACB-∠D=40°.
课堂练习:
变式:如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.求证:BD=DE.
证明:∵△ABC是等边三角形,BD是角平分线,
∴∠ABC=∠ACB=60°,∠DBC=30°.
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=30°.
∴∠DBC=∠DEC.
∴DB=DE(等角对等边).
例2: △ABC为正三角形,点M是BC边上任意一点,点N是CA边上任意一点,且BM=CN,BN与AM相交于Q点,∠BQM等于多少度?
解:∵△ABC为正三角形,
∴∠ABC=∠C=∠BAC=60°,AB=BC.
又∵BM=CN,
∴△AMB≌△BNC(SAS),
∴∠BAM=∠CBN,
∴∠BQM=∠ABQ+∠BAM
=∠ABQ+∠CBN=∠ABC=60°.
(二)等边三角形的判定
图形 等腰三角形 等边三角形
判定 从边看:两条边相等的三角形是等腰三角形 三条边都相等的三角形是等边三角形
从角看:两个角相等的三角形是等腰三角形 三个角都相等的三角形是等边三角形
等边三角形的判定方法:
有一个角是60°的等腰三角形是等边三角形.
用类比的方法从等腰三角形的判定方法分析得出等边三角形的判定方法,水到渠成,容易接受.
例2:如图,△ABC 是等边三角形,DE∥BC,分别交AB,AC 于点D,E.求证:△ADE 是等边三角形.
证明: ∵△ABC 是等边三角形,
∴∠A =∠B =∠C =60°.
∵DE∥BC,
∴∠B =∠ADE,∠C =∠AED.
∴∠A=∠ADE =∠AED.
∴△ADE 是等边三角形.
变式1:若点D、E 在边AB、AC 的延长线上,且DE∥BC,结论还成立吗?
证明:∵△ABC 是等边三角形,
∴∠A =∠ABC =∠ACB =60°.
∵DE∥BC,
∴∠ABC =∠ADE,∠ACB =∠AED.
∴∠A =∠ADE =∠AED.
∴△ADE 是等边三角形.
变式2:若点D、E 在边AB、AC 的反向延长线上,且DE∥BC,结论依然成立吗?
证明: ∵ △ABC 是等边三角形,
∴∠BAC =∠B =∠C =60°.
∵DE∥BC,
∴∠B =∠D,∠C =∠E.
∴∠EAD =∠D =∠E.
∴△ADE 是等边三角形.
变式3:上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗 试说明理由.
证明:∵ △ABC是等边三角形,
∴ ∠A=∠B=∠C.
∵ AD=AE,
∴ ∠ADE=∠B, ∠AED=∠C.
∴ ∠A=∠ADE= ∠AED.
∴ △ADE是等边三角形.
课堂练习:
1. 以下叙述中不正确的是( C )
A.等边三角形的每条高线都是角平分线和中线
B.其中有一内角为60°的等腰三角形是等边三角形
C.等腰三角形一定是锐角三角形
D.在一个三角形中,如果两条边不相等,那么它们所对的角也不相等;反之,在一个三角形中,如果两个角不相等,那么它们所对的边也不相等.
2. 已知等边三角形ABC的边长为6,D是AB上的动点,过点D作DE⊥AC于点E,过点E作EF⊥BC于点F,过点F作FG⊥AB于点G,当点G与点D重合时,AD的长为( )
A.4 B.6 C.8 D.9
3.如图,等边△ABC中,D、E、F分别是各边上的一点,且AD=BE=CF.
求证:△DEF是等边三角形.
证明:∵△ABC为等边三角形,且AD=BE=CF
∴AF=BD=CE,∠A=∠B=∠C=60°,
∴△ADF≌△BED≌△CFE(SAS),
∴DF=ED=EF,
∴△DEF是等边三角形.
课堂小结:
对比等腰三角形的性质与判定方法,说一说等边三角形的性质与判定方法.
注意等边三角形判定方法的特殊性:三边法、三角法、等腰三角形法.
作业布置:
1.等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试证明你的结论.
解:△APQ为等边三角形.
证明如下:∵△ABC为等边三角形,
∴AB=AC.
∵BP=CQ,∠ABP=∠ACQ,
∴△ABP≌△ACQ(SAS),
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
2.完成本节配套习题.
【板书设计】
等边三角形的定义,等腰三角形的底等腰;
等边三角形的性质:边、角、轴对称性;
等边三角形的判定方法:三边法、三角法、等腰三角形法.
【课后反思】
学习特殊的等腰三角形——等边三角形,让学生先通过画图,比较等方法自主探索,小组内、小组间充分交流后概括所得结论,这既巩固等腰三角形的应用知识,又类比探索等腰三角形性质和判定定理的方法,加深了对等腰三角形与等边三角形联系与区别的理解.
1
