初中数学人教版八上13.3.2等边三角形第2课时 习题(含解析)
文档属性
| 名称 | 初中数学人教版八上13.3.2等边三角形第2课时 习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 208.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-14 15:59:07 | ||
图片预览

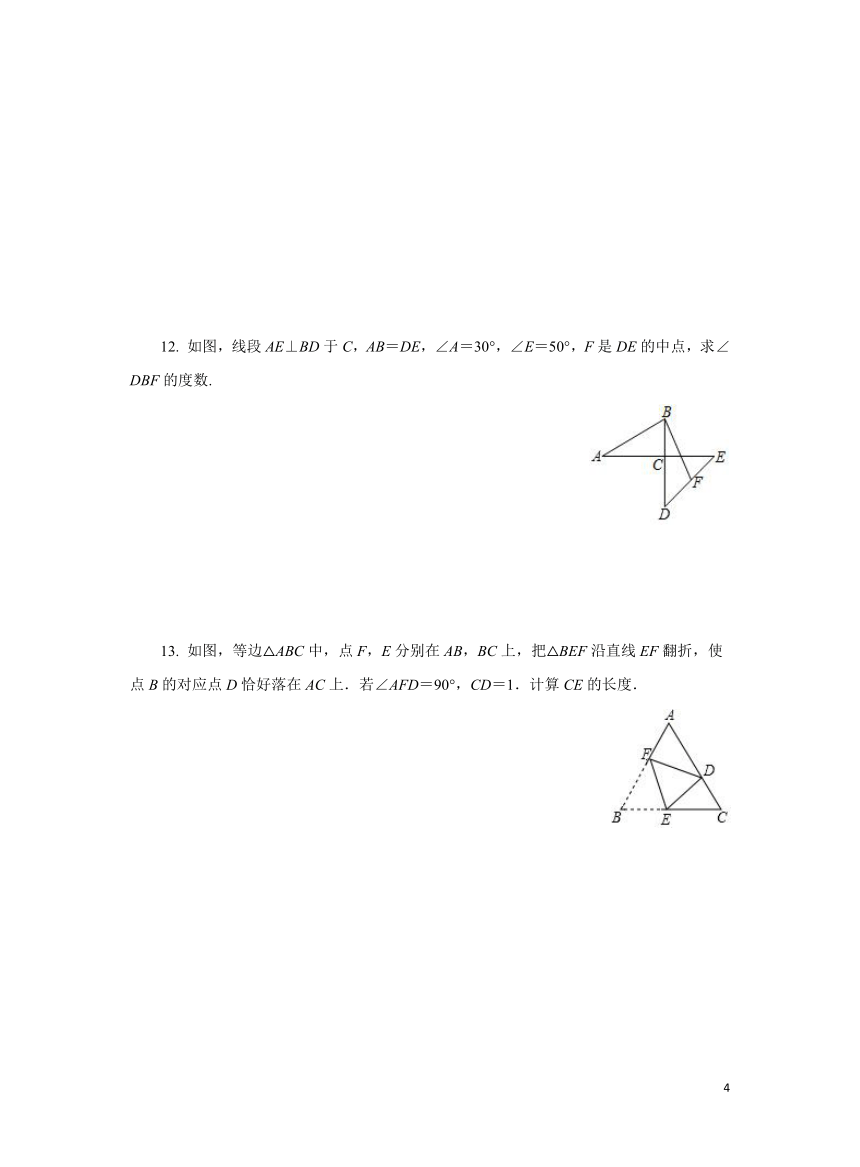
文档简介
13.3.2等边三角形(第2课时)
1. 如图,在等边△ABC中,BD平分∠ABC交AC于点D,过点D作DE⊥BC于点E,且CE=1.5,则AC的长为( )
A.3 B.4.5 C.6 D.7.5
2. 如图,△ABC是边长为6的等边三角形,D是BC上一点,BD=2,DE⊥BC交AB于点E,则AE=( )
A.2 B.3 C.4 D.5
3. 如图,已知∠AOB=60°,点P在OA边上,OP=8cm,点M、N在边OB上,PM=PN,若MN=2cm,则ON为( )
A.1cm B.3cm C.4cm D.5cm
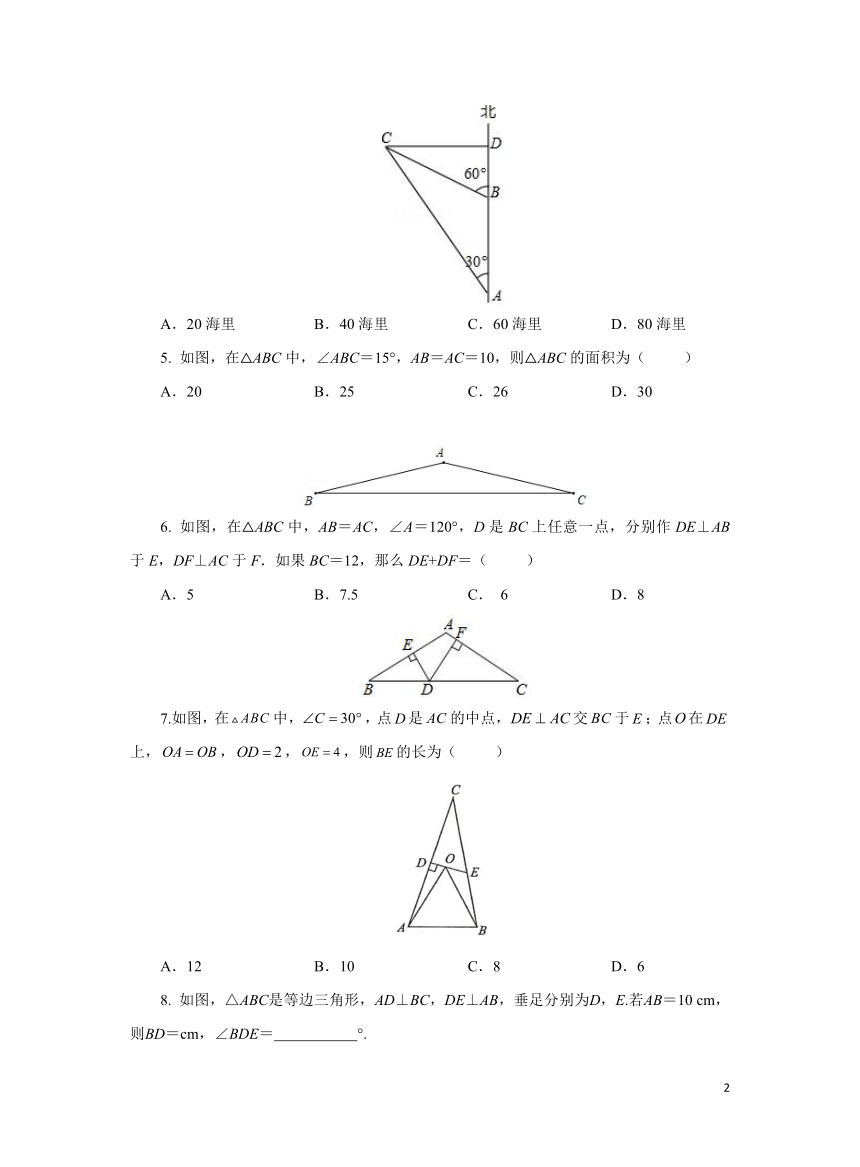
4. 如图,一艘轮船以每小时20海里的速度沿正北方航行,在A处测得灯塔C在北偏西30°方向上,轮船航行2小时后到达B处,在B处测得灯塔C在北偏西60°方向上,当轮船到达灯塔C的正东方向D处时,则轮船航程AD的距离是( )
A.20海里 B.40海里 C.60海里 D.80海里
5. 如图,在△ABC中,∠ABC=15°,AB=AC=10,则△ABC的面积为( )
A.20 B.25 C.26 D.30
6. 如图,在△ABC中,AB=AC,∠A=120°,D是BC上任意一点,分别作DE⊥AB于E,DF⊥AC于F.如果BC=12,那么DE+DF=( )
A.5 B.7.5 C. 6 D.8
7.如图,在中,,点是的中点,交于;点在上,,,,则的长为( )
A.12 B.10 C.8 D.6
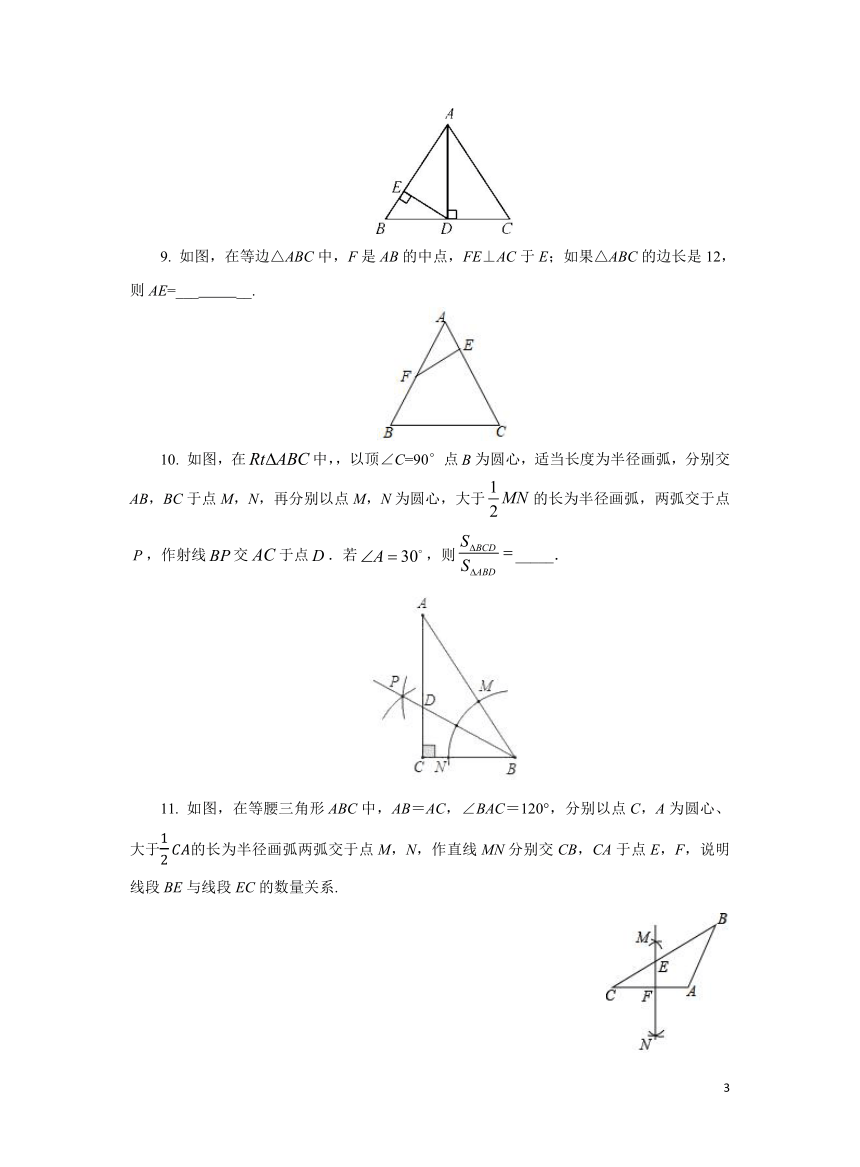
8. 如图,△ABC是等边三角形,AD⊥BC,DE⊥AB,垂足分别为D,E.若AB=10 cm,则BD=cm,∠BDE= °.
9. 如图,在等边△ABC中,F是AB的中点,FE⊥AC于E;如果△ABC的边长是12,则AE=___ __.
10. 如图,在中,,以顶∠C=90°点为圆心,适当长度为半径画弧,分别交AB,BC于点M,N,再分别以点M,N为圆心,大于的长为半径画弧,两弧交于点,作射线交于点.若,则_____.
11. 如图,在等腰三角形ABC中,AB=AC,∠BAC=120°,分别以点C,A为圆心、大于的长为半径画弧两弧交于点M,N,作直线MN分别交CB,CA于点E,F,说明线段BE与线段EC的数量关系.
12. 如图,线段AE⊥BD于C,AB=DE,∠A=30°,∠E=50°,F是DE的中点,求∠DBF的度数.
13. 如图,等边△ABC中,点F,E分别在AB,BC上,把△BEF沿直线EF翻折,使点B的对应点D恰好落在AC上.若∠AFD=90°,CD=1.计算CE的长度.
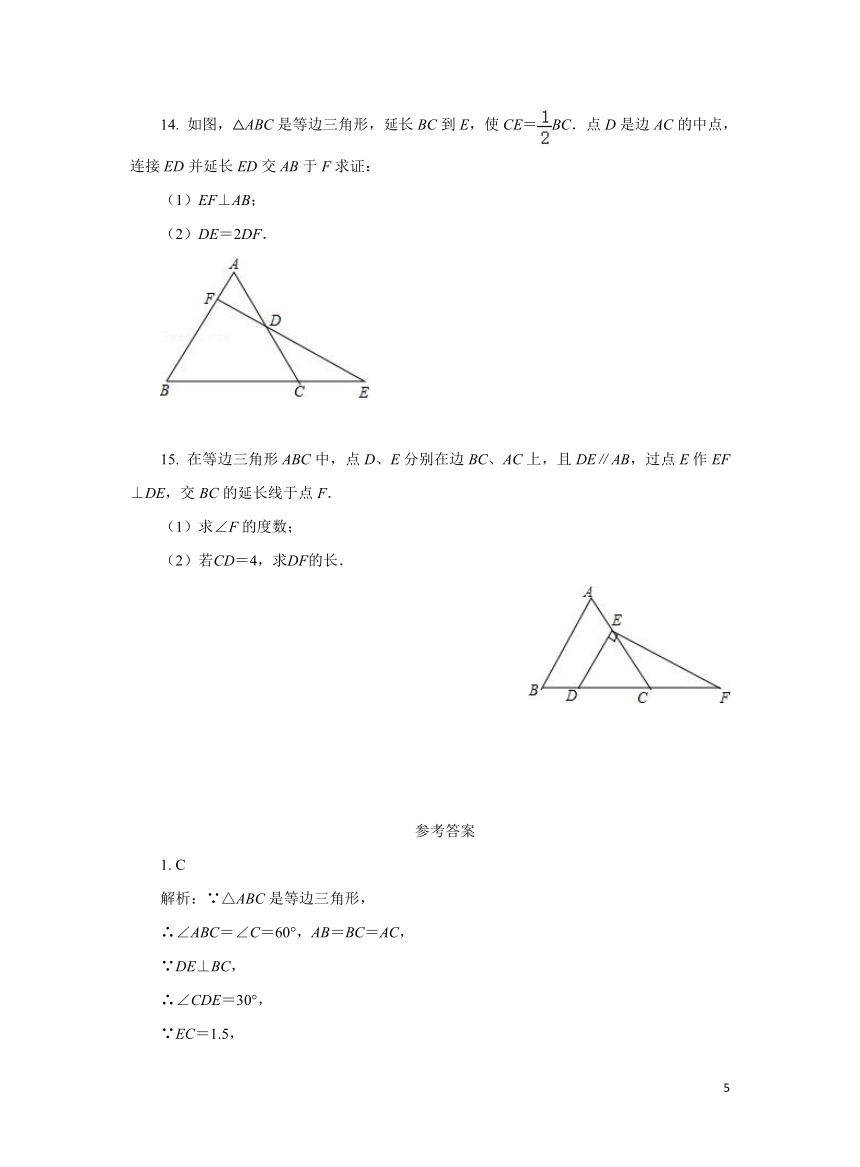
14. 如图,△ABC是等边三角形,延长BC到E,使CE=BC.点D是边AC的中点,连接ED并延长ED交AB于F求证:
(1)EF⊥AB;
(2)DE=2DF.
15. 在等边三角形ABC中,点D、E分别在边BC、AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=4,求DF的长.
参考答案
1. C
解析:∵△ABC是等边三角形,
∴∠ABC=∠C=60°,AB=BC=AC,
∵DE⊥BC,
∴∠CDE=30°,
∵EC=1.5,
∴CD=2EC=3,
∵BD平分∠ABC交AC于点D,
∴AD=CD=3,
∴AC=AD+CD=6.
2. A
解析:∵△ABC是等边三角形,
∴∠B=60°,
∵DE⊥BC,
∴∠EDB=90°,∠BED=30°,
∵BD=2,
∴EB=2BD=4,
∴AE=AB﹣BE=6﹣4=2.
3.D
解析:过P作PD⊥OB于D,
∵PM=PN,MN=2cm,
∴MD=ND=1cm,
∵PD⊥OB,
∴∠PDO=90°,
∵∠POB=60°,
∴∠OPD=30°,
∴OD=OP,
∵OP=8cm,
∴OD=4cm,
∴ON=OD+ND=5cm.
4.C
解析:由题意得∠CAB=30°,∠CBD=60°,
∴∠ACB=30°,
∴BC=BA=2×20=40,
∵∠CDB=90°,
∴BD=BC=20,
∴AD=BD+AB=20+40=60,
则轮船航程AD的距离是60海里.
5.B
解析:过B点作BD⊥AC,交CA的延长线于点D,
,
∵AB=AC,∠ABC=15°,
∴∠C=∠ABC=15°,
∴∠DAB=∠ABC+∠C=30°,
∵AB=AC=10,
∴BD=AB=5,
∴△ABC的面积为:.
6. C
解析:∵AB=AC,∠A=120°,
∴∠B=∠C=30°.
∵DE⊥AB于E,DF⊥AC于F,
∴DE=BD,DF=CD.
∵BC=12,
∴DE+DF=BC=6.
7. C
解:连接OC,过点O作于F,如图,
∵,,
∴,
在Rt△CDE中,,
∴,,
∵D为AC的中点,,
∴,
∵,
∴,
∵,
∴,
在Rt△OEF中,
∵,
∴,
∴,
∴,
∴.
8.5;30
解析:∵△ABC是等边三角形,
∴BC=AB=10cm,∠BAC=60°,
又∵AD⊥BC,
∴BD=∠BAC=30°.
9. 3
解析:∵△ABC是等边三角形,∴∠A=60°.
∵EF⊥AC,
∴∠AFE=30°.
∴AE=AF=AB=3.
10.
解析:由作法得平分,
∵,,
∴,
∴,
∴,
在中,,
∴,
∴.
11.解:BE=2EC,理由如下:
在△ABC中,AB=AC,∠BC=120°,
∴∠B=∠C=30°.
如图,连接EA,
由尺规作图可知直线MN是线段CA的垂直平分线,
∴EA=EC,
∴∠EAC=∠ECA=30°,
∴∠BAE=∠BAC﹣∠EAC=90°.
在Rt△BAE中,∠B=30°,
∴BE=2EA,
∴BE=2EC.
12. 解:连接CF,
∵AE⊥BD,
∴∠ACB=∠DCE=90°,
∵F为DE中点,∠A=30°,
∴CF=DF=EFDE,CBAB,
∵AB=DE,
∴BC=CF,
∴∠DBF=∠CFB,
∵CF=DF,
∴∠D=∠DCF,
∵∠DCE=90°,∠E=50°,
∴∠D=40°,
∴∠DCF=40°,
∵∠DBF=∠CFB,∠DBF+∠CFB=∠DCF,
∴∠DBF20°.
13. 解:∵把△BEF沿直线EF翻折,使点B的对应点D恰好落在AC上.
∠AFD=90°,
∴∠BFE=∠EFD=45°,
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠FEB=∠FED=180°﹣45°﹣60°=75°,
∴∠DEC=180°﹣75°﹣75°=30°,
∴∠EDC=180°﹣30°﹣60°=90°,
∵CD=1,
∴CE=2.
14.证明:(1)∵△ABC是等边三角形,
∴AC=BC,∠ACB=∠B=60°,
∵D为AC的中点,
∴AD=CD=AC,
∵CE=BC,
∴CD=CE,
∵∠E+∠CDE=∠ACB=60°,
∴∠E=∠CDE=30°,
∵∠B=60°,
∴∠EFB=180°﹣60°﹣30°=90°,
即EF⊥AB;
(2)连接BD,
∵△ABC是等边三角形,
∴AB=BC,∠ABC=60°,
∵D为AC的中点,
∴∠DBC=∠ABD=ABC=30°,
∵∠E=30°,
∴∠DBC=∠E,
∴DE=BD,
∵∠BFE=90°,∠ABD=30°,
∴BD=2DF,
即DE=2DF.
15. 解:(1)∵△ABC是等边三角形,
∴∠B=60°,
∵DE∥AB,
∴∠EDC=∠B=60°,
∵EF⊥DE,
∴∠DEF=90°,
∴∠F=90°﹣∠EDC=30°;
(2)∵∠ACB=60°,∠EDC=60°,
∴△EDC是等边三角形.
∴ED=DC=4,
∵∠DEF=90°,∠F=30°,
∴DF=2DE=8.
1
1. 如图,在等边△ABC中,BD平分∠ABC交AC于点D,过点D作DE⊥BC于点E,且CE=1.5,则AC的长为( )
A.3 B.4.5 C.6 D.7.5
2. 如图,△ABC是边长为6的等边三角形,D是BC上一点,BD=2,DE⊥BC交AB于点E,则AE=( )
A.2 B.3 C.4 D.5
3. 如图,已知∠AOB=60°,点P在OA边上,OP=8cm,点M、N在边OB上,PM=PN,若MN=2cm,则ON为( )
A.1cm B.3cm C.4cm D.5cm
4. 如图,一艘轮船以每小时20海里的速度沿正北方航行,在A处测得灯塔C在北偏西30°方向上,轮船航行2小时后到达B处,在B处测得灯塔C在北偏西60°方向上,当轮船到达灯塔C的正东方向D处时,则轮船航程AD的距离是( )
A.20海里 B.40海里 C.60海里 D.80海里
5. 如图,在△ABC中,∠ABC=15°,AB=AC=10,则△ABC的面积为( )
A.20 B.25 C.26 D.30
6. 如图,在△ABC中,AB=AC,∠A=120°,D是BC上任意一点,分别作DE⊥AB于E,DF⊥AC于F.如果BC=12,那么DE+DF=( )
A.5 B.7.5 C. 6 D.8
7.如图,在中,,点是的中点,交于;点在上,,,,则的长为( )
A.12 B.10 C.8 D.6
8. 如图,△ABC是等边三角形,AD⊥BC,DE⊥AB,垂足分别为D,E.若AB=10 cm,则BD=cm,∠BDE= °.
9. 如图,在等边△ABC中,F是AB的中点,FE⊥AC于E;如果△ABC的边长是12,则AE=___ __.
10. 如图,在中,,以顶∠C=90°点为圆心,适当长度为半径画弧,分别交AB,BC于点M,N,再分别以点M,N为圆心,大于的长为半径画弧,两弧交于点,作射线交于点.若,则_____.
11. 如图,在等腰三角形ABC中,AB=AC,∠BAC=120°,分别以点C,A为圆心、大于的长为半径画弧两弧交于点M,N,作直线MN分别交CB,CA于点E,F,说明线段BE与线段EC的数量关系.
12. 如图,线段AE⊥BD于C,AB=DE,∠A=30°,∠E=50°,F是DE的中点,求∠DBF的度数.
13. 如图,等边△ABC中,点F,E分别在AB,BC上,把△BEF沿直线EF翻折,使点B的对应点D恰好落在AC上.若∠AFD=90°,CD=1.计算CE的长度.
14. 如图,△ABC是等边三角形,延长BC到E,使CE=BC.点D是边AC的中点,连接ED并延长ED交AB于F求证:
(1)EF⊥AB;
(2)DE=2DF.
15. 在等边三角形ABC中,点D、E分别在边BC、AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=4,求DF的长.
参考答案
1. C
解析:∵△ABC是等边三角形,
∴∠ABC=∠C=60°,AB=BC=AC,
∵DE⊥BC,
∴∠CDE=30°,
∵EC=1.5,
∴CD=2EC=3,
∵BD平分∠ABC交AC于点D,
∴AD=CD=3,
∴AC=AD+CD=6.
2. A
解析:∵△ABC是等边三角形,
∴∠B=60°,
∵DE⊥BC,
∴∠EDB=90°,∠BED=30°,
∵BD=2,
∴EB=2BD=4,
∴AE=AB﹣BE=6﹣4=2.
3.D
解析:过P作PD⊥OB于D,
∵PM=PN,MN=2cm,
∴MD=ND=1cm,
∵PD⊥OB,
∴∠PDO=90°,
∵∠POB=60°,
∴∠OPD=30°,
∴OD=OP,
∵OP=8cm,
∴OD=4cm,
∴ON=OD+ND=5cm.
4.C
解析:由题意得∠CAB=30°,∠CBD=60°,
∴∠ACB=30°,
∴BC=BA=2×20=40,
∵∠CDB=90°,
∴BD=BC=20,
∴AD=BD+AB=20+40=60,
则轮船航程AD的距离是60海里.
5.B
解析:过B点作BD⊥AC,交CA的延长线于点D,
,
∵AB=AC,∠ABC=15°,
∴∠C=∠ABC=15°,
∴∠DAB=∠ABC+∠C=30°,
∵AB=AC=10,
∴BD=AB=5,
∴△ABC的面积为:.
6. C
解析:∵AB=AC,∠A=120°,
∴∠B=∠C=30°.
∵DE⊥AB于E,DF⊥AC于F,
∴DE=BD,DF=CD.
∵BC=12,
∴DE+DF=BC=6.
7. C
解:连接OC,过点O作于F,如图,
∵,,
∴,
在Rt△CDE中,,
∴,,
∵D为AC的中点,,
∴,
∵,
∴,
∵,
∴,
在Rt△OEF中,
∵,
∴,
∴,
∴,
∴.
8.5;30
解析:∵△ABC是等边三角形,
∴BC=AB=10cm,∠BAC=60°,
又∵AD⊥BC,
∴BD=∠BAC=30°.
9. 3
解析:∵△ABC是等边三角形,∴∠A=60°.
∵EF⊥AC,
∴∠AFE=30°.
∴AE=AF=AB=3.
10.
解析:由作法得平分,
∵,,
∴,
∴,
∴,
在中,,
∴,
∴.
11.解:BE=2EC,理由如下:
在△ABC中,AB=AC,∠BC=120°,
∴∠B=∠C=30°.
如图,连接EA,
由尺规作图可知直线MN是线段CA的垂直平分线,
∴EA=EC,
∴∠EAC=∠ECA=30°,
∴∠BAE=∠BAC﹣∠EAC=90°.
在Rt△BAE中,∠B=30°,
∴BE=2EA,
∴BE=2EC.
12. 解:连接CF,
∵AE⊥BD,
∴∠ACB=∠DCE=90°,
∵F为DE中点,∠A=30°,
∴CF=DF=EFDE,CBAB,
∵AB=DE,
∴BC=CF,
∴∠DBF=∠CFB,
∵CF=DF,
∴∠D=∠DCF,
∵∠DCE=90°,∠E=50°,
∴∠D=40°,
∴∠DCF=40°,
∵∠DBF=∠CFB,∠DBF+∠CFB=∠DCF,
∴∠DBF20°.
13. 解:∵把△BEF沿直线EF翻折,使点B的对应点D恰好落在AC上.
∠AFD=90°,
∴∠BFE=∠EFD=45°,
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠FEB=∠FED=180°﹣45°﹣60°=75°,
∴∠DEC=180°﹣75°﹣75°=30°,
∴∠EDC=180°﹣30°﹣60°=90°,
∵CD=1,
∴CE=2.
14.证明:(1)∵△ABC是等边三角形,
∴AC=BC,∠ACB=∠B=60°,
∵D为AC的中点,
∴AD=CD=AC,
∵CE=BC,
∴CD=CE,
∵∠E+∠CDE=∠ACB=60°,
∴∠E=∠CDE=30°,
∵∠B=60°,
∴∠EFB=180°﹣60°﹣30°=90°,
即EF⊥AB;
(2)连接BD,
∵△ABC是等边三角形,
∴AB=BC,∠ABC=60°,
∵D为AC的中点,
∴∠DBC=∠ABD=ABC=30°,
∵∠E=30°,
∴∠DBC=∠E,
∴DE=BD,
∵∠BFE=90°,∠ABD=30°,
∴BD=2DF,
即DE=2DF.
15. 解:(1)∵△ABC是等边三角形,
∴∠B=60°,
∵DE∥AB,
∴∠EDC=∠B=60°,
∵EF⊥DE,
∴∠DEF=90°,
∴∠F=90°﹣∠EDC=30°;
(2)∵∠ACB=60°,∠EDC=60°,
∴△EDC是等边三角形.
∴ED=DC=4,
∵∠DEF=90°,∠F=30°,
∴DF=2DE=8.
1
