高一数学(下)期末总复习-统计(江苏省宿迁市沭阳县)
文档属性
| 名称 | 高一数学(下)期末总复习-统计(江苏省宿迁市沭阳县) |  | |
| 格式 | rar | ||
| 文件大小 | 73.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-03-18 15:38:00 | ||
图片预览


文档简介
影响力位居国内前列教育资源网
21世纪教育网www.21cnjy.com
高一数学(下)期末总复习—统计
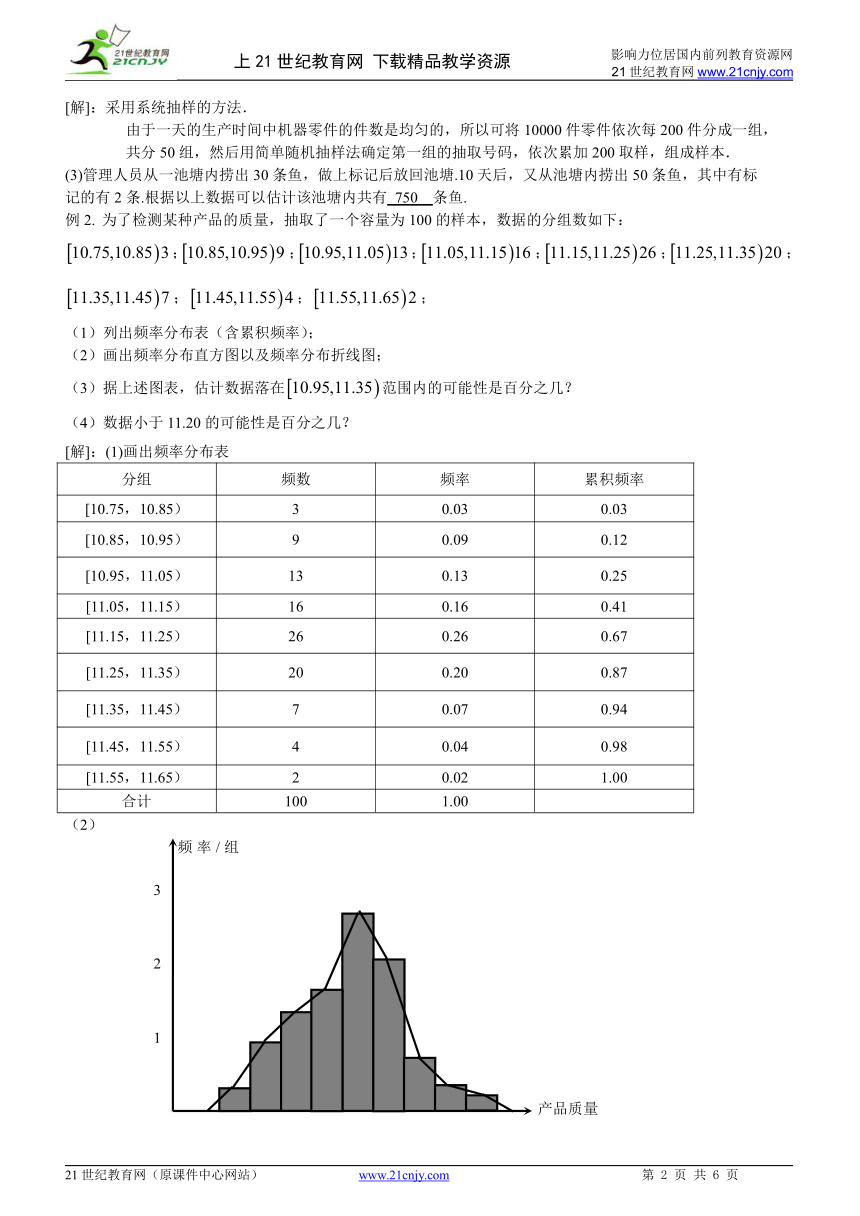
1、 知识结构:
(1)抽样方法
简单随机抽样:对于一个总体,只要是通过逐个抽取的方法从中抽取一个样本,而且每次抽取时各个
个体被抽到的概率相等,这样的抽样方法叫简单随机抽样.
分层抽样:将总体中的个体按不同特点分类,形成几个层次上的不同部分,然后按照各部分所占的比
重实施抽样,这样的抽样方法叫分层抽样.
系统抽样:将总体平均分成几个部分,按照一定规则,从每个部分抽取一个个体作为样本.
(2)总体分布的估计
频数 频率 累积频率 直方图 茎叶图
(3)总体的期望和方差
总体的期望和方差用样本的期望值和方差来估计.
样本的平均数(期望值)=( x1+x2+…+xn)
方差:S2=[( x1-1 )2+(x2-)2+…+(xn-)2]
(4)线形回归方程
2、 例题解析:
例1. (1)某住宅小区有居民2万户,从中随机抽取200户,调查是否安装电话,调查的结果如图所示,则该
小区已安装电话的户数动迁户、原住户估计分别有 6500 、 3000 .
电话 动迁户 原住户
已安装 65 30
未安装 40 65
(2)某工厂平均每天生产某种机器零件大约10000件,要求产品检验员每天抽取50件零件,检查其质量情
况;假设一天的生产时间中生产机器零件的件数是均匀的,请你设计一个调查方案.
[解]:采用系统抽样的方法.
由于一天的生产时间中机器零件的件数是均匀的,所以可将10000件零件依次每200件分成一组,
共分50组,然后用简单随机抽样法确定第一组的抽取号码,依次累加200取样,组成样本.
(3)管理人员从一池塘内捞出30条鱼,做上标记后放回池塘.10天后,又从池塘内捞出50条鱼,其中有标
记的有2条.根据以上数据可以估计该池塘内共有 750 条鱼.
例2. 为了检测某种产品的质量,抽取了一个容量为100的样本,数据的分组数如下:
;;;;;;;;;
(1)列出频率分布表(含累积频率);
(2)画出频率分布直方图以及频率分布折线图;
(3)据上述图表,估计数据落在范围内的可能性是百分之几?
(4)数据小于11.20的可能性是百分之几?
[解]:(1)画出频率分布表
分组 频数 频率 累积频率
[10.75,10.85) 3 0.03 0.03
[10.85,10.95) 9 0.09 0.12
[10.95,11.05) 13 0.13 0.25
[11.05,11.15) 16 0.16 0.41
[11.15,11.25) 26 0.26 0.67
[11.25,11.35) 20 0.20 0.87
[11.35,11.45) 7 0.07 0.94
[11.45,11.55) 4 0.04 0.98
[11.55,11.65) 2 0.02 1.00
合计 100 1.00
(2)
(3)由上述图表可知数据落在范围内的频率为:,即数据
落在范围内的可能性是75%.
(4)数据小于11.20的可能性即数据小于11.20的频率,也就是数据在11.20处的累积频率.设为,
则:,
所以,从而估计数据小于11.20的可能性是54%.
例3:假设关于某设备的使用年限x和所支出的维修费用y(万元),有如下的统计资料:
若由资料知,y对x呈线性相关关系,试求:
(1) 画出上表的散点图;
(2) 求出回归直线并且画出图形
(3) 回归直线必经过的一点是哪一点?
[解]:(1)图略 (2)y=1.27x-0.08 (3) (4,5)
例4:某化肥厂有甲、乙两个车间包装肥料,在自动包装传送带上每隔30分钟抽取一包产品,称其重量,
分别记录抽查数据如下:
甲:102,101,99,98,103,98,99;
乙:110,115,90,85,75,115,110.
(1)这种抽样方法是哪一种方法?
(2)试计算甲、乙两个车间产品重量的平均数与方差,并说明哪个车间产品较稳定?
[解]:(1)采用的方法是:系统抽样;
(2);
;
;
;
∴ 故甲车间产品比较稳定.
三、反馈检测:
(一)选择题:1.某学校有六个年级,人数分别为200、200、180、150、150、120,为加强学校民主化管理,
拟就某项重大决策进行问卷调查,样本容量为100,下列做法符合统计学原理的是( D ).
A.午餐时间在食堂随意选定100人
B.先广播通知,然后在学生会门口将调查卷发给前100位来领取表格的同学
C.把全校学生编码,用计算机随机抽取100人,发给调查卷
D.把调查卷分给各年级,数目如下:20、20、18、15、15、12.由各年级给本年级学生编码,用计
算机随机抽取相应数目,发给问卷
2.下列抽样中不是系统抽样的是( C )
A、从标有1~15号的15个球中,任选三个作样本,按从小号到大号排序,随机选起点,以后
,(超过15则从1再数起)号入样;
B、工厂生产的产品,用传送带将产品送入包装车间前,检验人员从传送带上每隔五分钟抽一件产品进
行检验;
C、搞某一市场调查,规定在商场门口随机抽一个人进行询问调查,直到调查到事先规定的人数为止;
D、电影院调查观众的某一指标,通知每排(每排人数相同)座位号为14的观众留下座谈.
3.从2005个编号中抽取20个号码入样,采用系统抽样的方法,则抽样的间隔为( C )
A、99 B、99.5 C、100 D、100.5
4.某村有旱地与水田若干,现在需要估计平均亩产量,用按5%分层抽样的方法抽取15亩旱地45亩水田进
行调查,则这个村的旱地与水田的亩数分别是( B )
A、150,450; B、300,900; C、600,600; D、75,225.
5.下列两个变量之间的关系是相关关系的是(D )
A、正方体的棱长和体积 B、单位圆中角的度数和所对弧长
C、单产为常数时,土地面积和总产量 D、日照时间与水稻的亩产量
下列说法中,正确的是(D )
A. 频率分布直方图中各小长方形的面积不等于相应各组的频率
B.一组数据的标准差是这组数据的方差的平方
C.数据2,3,4,5的方差是数据4,6,8,10的方差的一半
D.一组数据的方差越大,说明这组数据的波动越大
6.已知某工厂工人某 加工的零件个数的茎叶图如右图所示
10111213 780222366677800122344667880234
(以零件个数的前两位为茎,后一位为叶),那么工人生产零件
的平均个数及生产的零件个数超过130的比例分别是 (B )
A. 116.5与13.3% B. 120.5与10%
C. 120.5与13.3% D. 126.5与10%
7.工人月工资(元)依劳动生产率(千元)变化的回归直线方程为,下列判断正确的是()
(A)劳动生产率为1000元时,工资为50元
(B)劳动生产率提高1000元时,工资提高150元
(C)劳动生产率提高1000元时,工资提高90元
(D)劳动生产率为1000元时,工资为90元
8.已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是(C )
A.=1.23x+4 B. =1.23x+5
C. =1.23x+0.08 D. =0.08x+1.23
(二)填空题:
9. 一个总体中共有200个个体,用简单随机抽样的方法从中抽取一个容量为20的样本,则某一特定个体被
抽到的可能性是 0.1 .
10.某所大学的计算机工程学院的大一新生有160人,其中男生95人,女生65人,现在要抽取一个容量为
20的样本,若用分层抽样,女生应抽取__8____人.
11.将参加数学竞赛的1000名学生编号如下:0001,0002,0003,…,1000,打算从中抽取一个容量为那50的
样本,按系统抽样的方法分成50个部分,如果第一部分编号为0001,0002,0003,…,0020,第一部分随机
抽取一个号码为0015,则抽取的第40个号码为 0795 .
12.为了了解某地区高三学生身体发育情况,抽查了该地区100名年龄为17.5岁~18岁的男生体重(kg) ,得到频率分直方图,如图.根据右图可得这100名学生中体重在〔56.5,64.5〕的学生人数是40 .
13.数据 平均数为6,标准差为2,则数据 的平均数为 6 ,方差为 16 .
14.200辆汽车通过某一段公路时的时速频率
分布直方图如图所示,
则时速在的汽
车大约有 60 辆.
(三)解答题:
15.已知某天一工厂甲、乙、丙三个车间生产的产品件数分别是1500、1300、1200,为了掌握各车间的生产
质量情况,要从中取出一个容量为40的样本,按照分层抽样的方法取样时,每个车间分别抽取多少件产品?
[解]:甲车间应抽取的件数为:;
乙车间应抽取的件数为:;
丙车间应抽取的件数为:.
16.下表是某中学对本校初中二年级女生身高情况进行抽测
后所得的部分资料(身高单位:cm,测量时精确到1cm).
已知身高在151cm (含151cm)以下的被测女生共3人.
⑴ 求所有被测女生总数;
⑵ 求身高在161cm (含161cm)以上的被测女生数;
⑶ 完成频率分布直方图.
分 组 频 率
[145.5,148.5) 0.02
[148.5,151.5) 0.04
[151.5,154.5) 0.08
[154.5,157.5) 0.12
[157.5,160.5) 0.30
[160.5,163.5) 0.20
[163.5,166.5) 0.18
[166.5,169.5] 0.06
[解]:⑴ =50(人)
⑵(0.2+0.18+0.06)×50=22(人)⑶要点:横轴:身高/cm;纵轴:频率/组距;
长方形的高的比例:1:2:4:6:15:10:9:3.
17.(1)为了比较甲,乙两位射击运动员的成绩,在相同的条件下对他们进行了10次测验,测得他们的环数如下:
环数 10 9 8 7 6 5
甲(次) 3 2 1 2 0 2
乙(次) 2 2 2 2 2 0
试根据以上数据,判断他们谁更优秀.
[解]:=8,=8, =3.4,=2, 所以乙更优秀
(2)已知一组数据求这组数据的平均
数.
[解]:
18.要分析学生初中升学的数学成绩对高一年级数学学习的影响,在高一年级学生中随机抽取10名学生,分析
他们入学的数学成绩和高一期末数学考试成绩(如下表):
学生编号 1 2 3 4 5 6 7 8 9 10
入学成绩x 63 67 45 88 81 71 52 99 58 76
高一期末成绩y 65 78 52 82 92 89 73 98 56 75
(1) 计算入学成绩x与高一期末成绩y的相关关系;
(2) 若线性相关,求出回归方程;
(3) 若某学生入学数学成绩为80分,试估计他高一期末数学成绩.
[解]:(1)r=0.839786, 线性相关;(2)y=0.76556x+22.41067;(3)84分.
总体
抽样
分析
估计
简单随机抽样
系统抽样
分层抽样
样本分布
样本特征数
相关系数
总体分布
总体特征数
相关系数
频率/组距
1
2
3
产品质量
频率
0.4
0.2
0.1
0
40 50 60 70 80 时速
21世纪教育网(原课件中心网站) www.21cnjy.com 第 6 页 共 6 页
21世纪教育网www.21cnjy.com
高一数学(下)期末总复习—统计
1、 知识结构:
(1)抽样方法
简单随机抽样:对于一个总体,只要是通过逐个抽取的方法从中抽取一个样本,而且每次抽取时各个
个体被抽到的概率相等,这样的抽样方法叫简单随机抽样.
分层抽样:将总体中的个体按不同特点分类,形成几个层次上的不同部分,然后按照各部分所占的比
重实施抽样,这样的抽样方法叫分层抽样.
系统抽样:将总体平均分成几个部分,按照一定规则,从每个部分抽取一个个体作为样本.
(2)总体分布的估计
频数 频率 累积频率 直方图 茎叶图
(3)总体的期望和方差
总体的期望和方差用样本的期望值和方差来估计.
样本的平均数(期望值)=( x1+x2+…+xn)
方差:S2=[( x1-1 )2+(x2-)2+…+(xn-)2]
(4)线形回归方程
2、 例题解析:
例1. (1)某住宅小区有居民2万户,从中随机抽取200户,调查是否安装电话,调查的结果如图所示,则该
小区已安装电话的户数动迁户、原住户估计分别有 6500 、 3000 .
电话 动迁户 原住户
已安装 65 30
未安装 40 65
(2)某工厂平均每天生产某种机器零件大约10000件,要求产品检验员每天抽取50件零件,检查其质量情
况;假设一天的生产时间中生产机器零件的件数是均匀的,请你设计一个调查方案.
[解]:采用系统抽样的方法.
由于一天的生产时间中机器零件的件数是均匀的,所以可将10000件零件依次每200件分成一组,
共分50组,然后用简单随机抽样法确定第一组的抽取号码,依次累加200取样,组成样本.
(3)管理人员从一池塘内捞出30条鱼,做上标记后放回池塘.10天后,又从池塘内捞出50条鱼,其中有标
记的有2条.根据以上数据可以估计该池塘内共有 750 条鱼.
例2. 为了检测某种产品的质量,抽取了一个容量为100的样本,数据的分组数如下:
;;;;;;;;;
(1)列出频率分布表(含累积频率);
(2)画出频率分布直方图以及频率分布折线图;
(3)据上述图表,估计数据落在范围内的可能性是百分之几?
(4)数据小于11.20的可能性是百分之几?
[解]:(1)画出频率分布表
分组 频数 频率 累积频率
[10.75,10.85) 3 0.03 0.03
[10.85,10.95) 9 0.09 0.12
[10.95,11.05) 13 0.13 0.25
[11.05,11.15) 16 0.16 0.41
[11.15,11.25) 26 0.26 0.67
[11.25,11.35) 20 0.20 0.87
[11.35,11.45) 7 0.07 0.94
[11.45,11.55) 4 0.04 0.98
[11.55,11.65) 2 0.02 1.00
合计 100 1.00
(2)
(3)由上述图表可知数据落在范围内的频率为:,即数据
落在范围内的可能性是75%.
(4)数据小于11.20的可能性即数据小于11.20的频率,也就是数据在11.20处的累积频率.设为,
则:,
所以,从而估计数据小于11.20的可能性是54%.
例3:假设关于某设备的使用年限x和所支出的维修费用y(万元),有如下的统计资料:
若由资料知,y对x呈线性相关关系,试求:
(1) 画出上表的散点图;
(2) 求出回归直线并且画出图形
(3) 回归直线必经过的一点是哪一点?
[解]:(1)图略 (2)y=1.27x-0.08 (3) (4,5)
例4:某化肥厂有甲、乙两个车间包装肥料,在自动包装传送带上每隔30分钟抽取一包产品,称其重量,
分别记录抽查数据如下:
甲:102,101,99,98,103,98,99;
乙:110,115,90,85,75,115,110.
(1)这种抽样方法是哪一种方法?
(2)试计算甲、乙两个车间产品重量的平均数与方差,并说明哪个车间产品较稳定?
[解]:(1)采用的方法是:系统抽样;
(2);
;
;
;
∴ 故甲车间产品比较稳定.
三、反馈检测:
(一)选择题:1.某学校有六个年级,人数分别为200、200、180、150、150、120,为加强学校民主化管理,
拟就某项重大决策进行问卷调查,样本容量为100,下列做法符合统计学原理的是( D ).
A.午餐时间在食堂随意选定100人
B.先广播通知,然后在学生会门口将调查卷发给前100位来领取表格的同学
C.把全校学生编码,用计算机随机抽取100人,发给调查卷
D.把调查卷分给各年级,数目如下:20、20、18、15、15、12.由各年级给本年级学生编码,用计
算机随机抽取相应数目,发给问卷
2.下列抽样中不是系统抽样的是( C )
A、从标有1~15号的15个球中,任选三个作样本,按从小号到大号排序,随机选起点,以后
,(超过15则从1再数起)号入样;
B、工厂生产的产品,用传送带将产品送入包装车间前,检验人员从传送带上每隔五分钟抽一件产品进
行检验;
C、搞某一市场调查,规定在商场门口随机抽一个人进行询问调查,直到调查到事先规定的人数为止;
D、电影院调查观众的某一指标,通知每排(每排人数相同)座位号为14的观众留下座谈.
3.从2005个编号中抽取20个号码入样,采用系统抽样的方法,则抽样的间隔为( C )
A、99 B、99.5 C、100 D、100.5
4.某村有旱地与水田若干,现在需要估计平均亩产量,用按5%分层抽样的方法抽取15亩旱地45亩水田进
行调查,则这个村的旱地与水田的亩数分别是( B )
A、150,450; B、300,900; C、600,600; D、75,225.
5.下列两个变量之间的关系是相关关系的是(D )
A、正方体的棱长和体积 B、单位圆中角的度数和所对弧长
C、单产为常数时,土地面积和总产量 D、日照时间与水稻的亩产量
下列说法中,正确的是(D )
A. 频率分布直方图中各小长方形的面积不等于相应各组的频率
B.一组数据的标准差是这组数据的方差的平方
C.数据2,3,4,5的方差是数据4,6,8,10的方差的一半
D.一组数据的方差越大,说明这组数据的波动越大
6.已知某工厂工人某 加工的零件个数的茎叶图如右图所示
10111213 780222366677800122344667880234
(以零件个数的前两位为茎,后一位为叶),那么工人生产零件
的平均个数及生产的零件个数超过130的比例分别是 (B )
A. 116.5与13.3% B. 120.5与10%
C. 120.5与13.3% D. 126.5与10%
7.工人月工资(元)依劳动生产率(千元)变化的回归直线方程为,下列判断正确的是()
(A)劳动生产率为1000元时,工资为50元
(B)劳动生产率提高1000元时,工资提高150元
(C)劳动生产率提高1000元时,工资提高90元
(D)劳动生产率为1000元时,工资为90元
8.已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是(C )
A.=1.23x+4 B. =1.23x+5
C. =1.23x+0.08 D. =0.08x+1.23
(二)填空题:
9. 一个总体中共有200个个体,用简单随机抽样的方法从中抽取一个容量为20的样本,则某一特定个体被
抽到的可能性是 0.1 .
10.某所大学的计算机工程学院的大一新生有160人,其中男生95人,女生65人,现在要抽取一个容量为
20的样本,若用分层抽样,女生应抽取__8____人.
11.将参加数学竞赛的1000名学生编号如下:0001,0002,0003,…,1000,打算从中抽取一个容量为那50的
样本,按系统抽样的方法分成50个部分,如果第一部分编号为0001,0002,0003,…,0020,第一部分随机
抽取一个号码为0015,则抽取的第40个号码为 0795 .
12.为了了解某地区高三学生身体发育情况,抽查了该地区100名年龄为17.5岁~18岁的男生体重(kg) ,得到频率分直方图,如图.根据右图可得这100名学生中体重在〔56.5,64.5〕的学生人数是40 .
13.数据 平均数为6,标准差为2,则数据 的平均数为 6 ,方差为 16 .
14.200辆汽车通过某一段公路时的时速频率
分布直方图如图所示,
则时速在的汽
车大约有 60 辆.
(三)解答题:
15.已知某天一工厂甲、乙、丙三个车间生产的产品件数分别是1500、1300、1200,为了掌握各车间的生产
质量情况,要从中取出一个容量为40的样本,按照分层抽样的方法取样时,每个车间分别抽取多少件产品?
[解]:甲车间应抽取的件数为:;
乙车间应抽取的件数为:;
丙车间应抽取的件数为:.
16.下表是某中学对本校初中二年级女生身高情况进行抽测
后所得的部分资料(身高单位:cm,测量时精确到1cm).
已知身高在151cm (含151cm)以下的被测女生共3人.
⑴ 求所有被测女生总数;
⑵ 求身高在161cm (含161cm)以上的被测女生数;
⑶ 完成频率分布直方图.
分 组 频 率
[145.5,148.5) 0.02
[148.5,151.5) 0.04
[151.5,154.5) 0.08
[154.5,157.5) 0.12
[157.5,160.5) 0.30
[160.5,163.5) 0.20
[163.5,166.5) 0.18
[166.5,169.5] 0.06
[解]:⑴ =50(人)
⑵(0.2+0.18+0.06)×50=22(人)⑶要点:横轴:身高/cm;纵轴:频率/组距;
长方形的高的比例:1:2:4:6:15:10:9:3.
17.(1)为了比较甲,乙两位射击运动员的成绩,在相同的条件下对他们进行了10次测验,测得他们的环数如下:
环数 10 9 8 7 6 5
甲(次) 3 2 1 2 0 2
乙(次) 2 2 2 2 2 0
试根据以上数据,判断他们谁更优秀.
[解]:=8,=8, =3.4,=2, 所以乙更优秀
(2)已知一组数据求这组数据的平均
数.
[解]:
18.要分析学生初中升学的数学成绩对高一年级数学学习的影响,在高一年级学生中随机抽取10名学生,分析
他们入学的数学成绩和高一期末数学考试成绩(如下表):
学生编号 1 2 3 4 5 6 7 8 9 10
入学成绩x 63 67 45 88 81 71 52 99 58 76
高一期末成绩y 65 78 52 82 92 89 73 98 56 75
(1) 计算入学成绩x与高一期末成绩y的相关关系;
(2) 若线性相关,求出回归方程;
(3) 若某学生入学数学成绩为80分,试估计他高一期末数学成绩.
[解]:(1)r=0.839786, 线性相关;(2)y=0.76556x+22.41067;(3)84分.
总体
抽样
分析
估计
简单随机抽样
系统抽样
分层抽样
样本分布
样本特征数
相关系数
总体分布
总体特征数
相关系数
频率/组距
1
2
3
产品质量
频率
0.4
0.2
0.1
0
40 50 60 70 80 时速
21世纪教育网(原课件中心网站) www.21cnjy.com 第 6 页 共 6 页
