2024人教版高中数学选择性必修第二册同步练习题(含解析)--专题强化练1 等差数列的综合应用
文档属性
| 名称 | 2024人教版高中数学选择性必修第二册同步练习题(含解析)--专题强化练1 等差数列的综合应用 |  | |
| 格式 | docx | ||
| 文件大小 | 982.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-16 13:37:31 | ||
图片预览

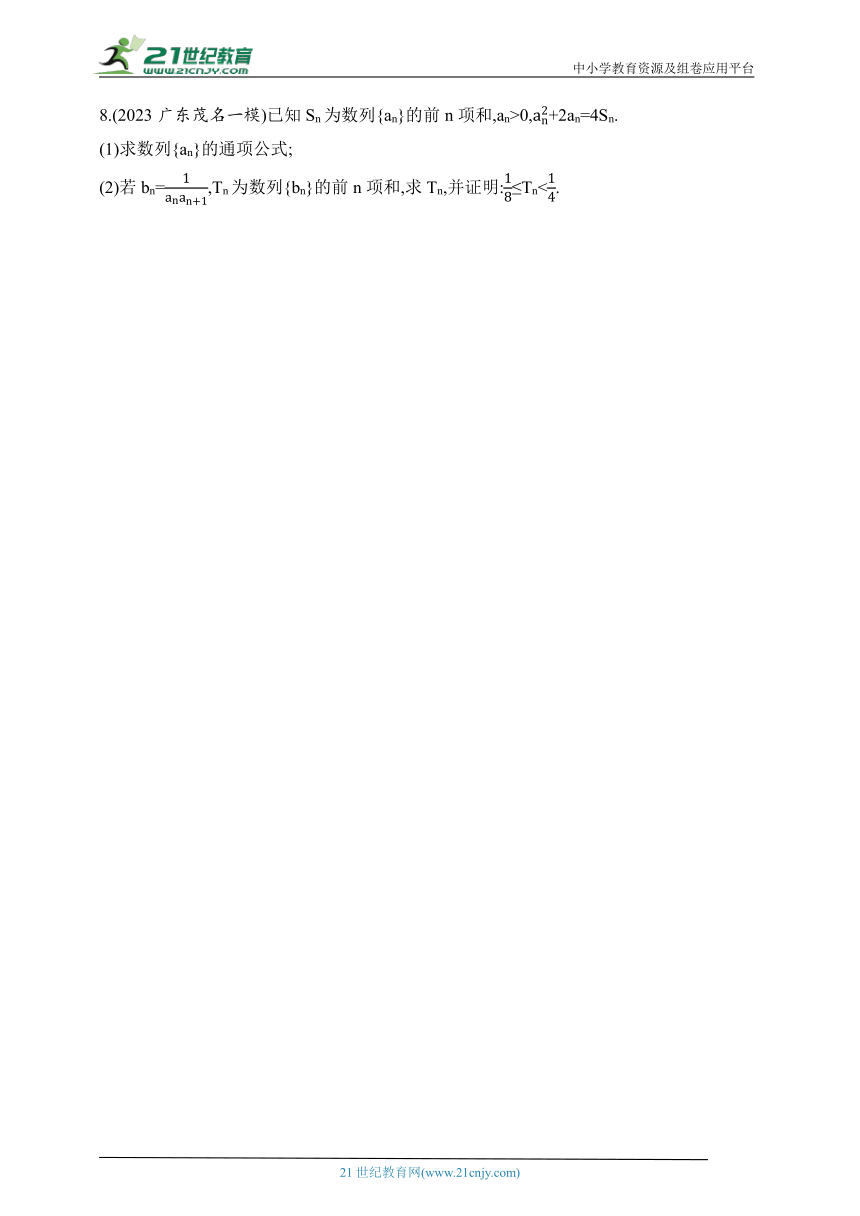

文档简介
中小学教育资源及组卷应用平台
2024人教版高中数学选择性必修第二册同步
专题强化练1 等差数列的综合应用
1.(2023河南郑州期末)设等差数列{an}的前n项和为Sn,a1=2,S8≥S7≥S9,则公差d的取值范围是( )
A. B.
C. D.
2.(2023河南南阳期末)已知等差数列{an}的各项均为正整数,若a1=1923,am=1953,an=2023,则m+n的最小值为( )
A.2 B.8 C.15 D.19
3.(2022江西宜春期末)某大楼共有12层,有11人在第一层上了电梯,他们分别要去第2至12层,每层1人,因特殊原因,电梯只能停在某一层,其余10人都要步行到所要去的楼层,假设初始的“不满意度”为0,每位乘客每向下步行1层的“不满意度”增量为1,每向上步行1层的“不满意度”增量为2,要使得10人的“不满意度”之和最小,电梯应该停在第几层( )
A.7 B.8 C.9 D.10
4.在等差数列{an}中,首项a1>0,公差d≠0,前n项和为Sn,则下列说法正确的是( )
A.若S3=S11,则必有S14=0
B.若S3=S11,则S8是{Sn}中最大的项
C.若S7>S8,则必有S8>S9
D.若S7>S8,则必有S6>S9
5.(2023广东清远期末)已知{an}为等差数列,a1+a3+a5=66,a2+a4+a6=57,则下列结论正确的是( )
A.{an}的公差为-2
B.{an}的通项公式为an=31-3n
C.{an}的前n项和为
D.{|an|}的前50项和为2575
6.(2023安徽六安示范高中期末)已知等差数列{an}的前n项和为Sn,S17=17,S5=S13,则数列{|an|}的前20项和是 .
7.(2023江苏苏州第十中学校月考)数列{an}与{bn}均为等差数列,其前n项和分别为Sn与Tn,若,则= ,使得为整数的n值个数为 .
8.(2023广东茂名一模)已知Sn为数列{an}的前n项和,an>0,+2an=4Sn.
(1)求数列{an}的通项公式;
(2)若bn=,Tn为数列{bn}的前n项和,求Tn,并证明:≤Tn<.
答案与分层梯度式解析
专题强化练1 等差数列的综合应用
1.A 2.C 3.C 4.ACD 5.BC
1.A 由题意得Sn=na1+d,
则 故-≤d≤-.故选A.
2.C 设等差数列{an}的公差为d(d∈N*),
由题意可知1953=1923+(m-1)d,
2023=1923+(n-1)d,
则d=,即
所以m+n=2+,因为m,n,d∈N*,所以当且仅当d=10时,m+n有最小值,为15,此时m=4,n=11.故选C.
3.C 设电梯所停的楼层是n(2≤n≤12,n∈N*),“不满意度”之和为S,则S=1+2+…+(n-2)+2×[1+2+…+(12-n)]=+157,其图象开口向上,对称轴为直线n=,
又∵n∈N*,
∴S在n=9时取最小值.故选C.
4.ACD 根据等差数列的性质,得S11-S3=a4+a5+…+a11=4(a7+a8),若S3=S11,则a7+a8=0,S14==7(a7+a8)=0.根据Sn关于n的图象,知当S3=S11时,对称轴方程是n==7,结合首项a1>0,可得S7是{Sn}中的最大项.若S7>S8,则a8<0,那么d<0,所以a9<0,所以S8>S9,S9-S6=a7+a8+a9=3a8<0,即S6>S9.故选ACD.
5.BC 设等差数列{an}的公差为d,前n项和为Sn,因为a1+a3+a5=3a3=66,a2+a4+a6=3a4=57,所以a3=22,a4=19,所以d=a4-a3=-3,故A错误;
a1=a3-2d=28,∴an=28+(n-1)×(-3)=31-3n,故B正确;
Sn=,故C正确;
易得a10=31-3×10=1>0,a11=31-3×11=-2<0,
∴{|an|}的前50项和为S10-(S50-S10)=-S50+2S10
==2565,故D错误.
故选BC.
6.答案 202
解析 ∵S17=17a9=17,∴a9=1,又∵S5=S13,
∴a6+a7+…+a12+a13=0,即a9+a10=0,
∴a10=-1,∴公差d=a10-a9=-2,
∴an=a9+(n-9)·d=19-2n,
∴Sn=·n=(18-n)·n,
故数列{|an|}的前20项和是|a1|+|a2|+…+|a9|+|a10|+…+|a20|=(a1+…+a9)-(a10+…+a20)=2S9-S20=162+40=202.
7.答案 ;2
解析 由等差数列的性质可得,
,
因为为整数,所以4能被n+1整除,
又n+1≥2,n∈N*,故n+1=2或n+1=4,
解得n=1或n=3,
所以使得为整数的n值个数为2.
8.解析 (1)∵+2an=4Sn,
∴当n=1时,+2a1=4S1,则=2a1,
又an>0,∴a1=2,
当n≥2时,由+2an=4Sn,得+2an-1=4Sn-1,
∴+2an-1)=4(Sn-Sn-1),
即=4an-2an+2an-1,
∴(an+an-1)(an-an-1)=2(an+an-1),
∵an>0,∴an-an-1=2,
∴数列{an}是以2为首项,2为公差的等差数列,
∴an=2+2(n-1)=2n.
(2)由(1)得an=2n,
则bn=,
∴Tn=
=,
∵.
又∵n∈N*,∴随着n的增大而减少,从而Tn随着n的增大而增大,∴Tn≥T1=.
综上所述,≤Tn<.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版高中数学选择性必修第二册同步
专题强化练1 等差数列的综合应用
1.(2023河南郑州期末)设等差数列{an}的前n项和为Sn,a1=2,S8≥S7≥S9,则公差d的取值范围是( )
A. B.
C. D.
2.(2023河南南阳期末)已知等差数列{an}的各项均为正整数,若a1=1923,am=1953,an=2023,则m+n的最小值为( )
A.2 B.8 C.15 D.19
3.(2022江西宜春期末)某大楼共有12层,有11人在第一层上了电梯,他们分别要去第2至12层,每层1人,因特殊原因,电梯只能停在某一层,其余10人都要步行到所要去的楼层,假设初始的“不满意度”为0,每位乘客每向下步行1层的“不满意度”增量为1,每向上步行1层的“不满意度”增量为2,要使得10人的“不满意度”之和最小,电梯应该停在第几层( )
A.7 B.8 C.9 D.10
4.在等差数列{an}中,首项a1>0,公差d≠0,前n项和为Sn,则下列说法正确的是( )
A.若S3=S11,则必有S14=0
B.若S3=S11,则S8是{Sn}中最大的项
C.若S7>S8,则必有S8>S9
D.若S7>S8,则必有S6>S9
5.(2023广东清远期末)已知{an}为等差数列,a1+a3+a5=66,a2+a4+a6=57,则下列结论正确的是( )
A.{an}的公差为-2
B.{an}的通项公式为an=31-3n
C.{an}的前n项和为
D.{|an|}的前50项和为2575
6.(2023安徽六安示范高中期末)已知等差数列{an}的前n项和为Sn,S17=17,S5=S13,则数列{|an|}的前20项和是 .
7.(2023江苏苏州第十中学校月考)数列{an}与{bn}均为等差数列,其前n项和分别为Sn与Tn,若,则= ,使得为整数的n值个数为 .
8.(2023广东茂名一模)已知Sn为数列{an}的前n项和,an>0,+2an=4Sn.
(1)求数列{an}的通项公式;
(2)若bn=,Tn为数列{bn}的前n项和,求Tn,并证明:≤Tn<.
答案与分层梯度式解析
专题强化练1 等差数列的综合应用
1.A 2.C 3.C 4.ACD 5.BC
1.A 由题意得Sn=na1+d,
则 故-≤d≤-.故选A.
2.C 设等差数列{an}的公差为d(d∈N*),
由题意可知1953=1923+(m-1)d,
2023=1923+(n-1)d,
则d=,即
所以m+n=2+,因为m,n,d∈N*,所以当且仅当d=10时,m+n有最小值,为15,此时m=4,n=11.故选C.
3.C 设电梯所停的楼层是n(2≤n≤12,n∈N*),“不满意度”之和为S,则S=1+2+…+(n-2)+2×[1+2+…+(12-n)]=+157,其图象开口向上,对称轴为直线n=,
又∵n∈N*,
∴S在n=9时取最小值.故选C.
4.ACD 根据等差数列的性质,得S11-S3=a4+a5+…+a11=4(a7+a8),若S3=S11,则a7+a8=0,S14==7(a7+a8)=0.根据Sn关于n的图象,知当S3=S11时,对称轴方程是n==7,结合首项a1>0,可得S7是{Sn}中的最大项.若S7>S8,则a8<0,那么d<0,所以a9<0,所以S8>S9,S9-S6=a7+a8+a9=3a8<0,即S6>S9.故选ACD.
5.BC 设等差数列{an}的公差为d,前n项和为Sn,因为a1+a3+a5=3a3=66,a2+a4+a6=3a4=57,所以a3=22,a4=19,所以d=a4-a3=-3,故A错误;
a1=a3-2d=28,∴an=28+(n-1)×(-3)=31-3n,故B正确;
Sn=,故C正确;
易得a10=31-3×10=1>0,a11=31-3×11=-2<0,
∴{|an|}的前50项和为S10-(S50-S10)=-S50+2S10
==2565,故D错误.
故选BC.
6.答案 202
解析 ∵S17=17a9=17,∴a9=1,又∵S5=S13,
∴a6+a7+…+a12+a13=0,即a9+a10=0,
∴a10=-1,∴公差d=a10-a9=-2,
∴an=a9+(n-9)·d=19-2n,
∴Sn=·n=(18-n)·n,
故数列{|an|}的前20项和是|a1|+|a2|+…+|a9|+|a10|+…+|a20|=(a1+…+a9)-(a10+…+a20)=2S9-S20=162+40=202.
7.答案 ;2
解析 由等差数列的性质可得,
,
因为为整数,所以4能被n+1整除,
又n+1≥2,n∈N*,故n+1=2或n+1=4,
解得n=1或n=3,
所以使得为整数的n值个数为2.
8.解析 (1)∵+2an=4Sn,
∴当n=1时,+2a1=4S1,则=2a1,
又an>0,∴a1=2,
当n≥2时,由+2an=4Sn,得+2an-1=4Sn-1,
∴+2an-1)=4(Sn-Sn-1),
即=4an-2an+2an-1,
∴(an+an-1)(an-an-1)=2(an+an-1),
∵an>0,∴an-an-1=2,
∴数列{an}是以2为首项,2为公差的等差数列,
∴an=2+2(n-1)=2n.
(2)由(1)得an=2n,
则bn=,
∴Tn=
=,
∵.
又∵n∈N*,∴随着n的增大而减少,从而Tn随着n的增大而增大,∴Tn≥T1=.
综上所述,≤Tn<.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
