2024人教版高中数学选择性必修第三册同步练习题(含解析)--第八章 成对数据的统计分析复习提升
文档属性
| 名称 | 2024人教版高中数学选择性必修第三册同步练习题(含解析)--第八章 成对数据的统计分析复习提升 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-16 17:56:07 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024人教版高中数学选择性必修第三册同步
第八章 成对数据的统计分析
本章复习提升
易混易错练
易错点1 选错回归模型致错
1.(2023湖南长沙长郡中学检测)某互联网公司为了确定下一季度的前期广告投入计划,收集了近6个月广告投入量x(单位:万元)和收益y(单位:万元)的数据,如下表所示:
月份 1 2 3 4 5 6
广告投入 量x(万元) 2 4 6 8 10 12
收益y(万元) 14.21 20.31 31.8 31.18 37.83 44.67
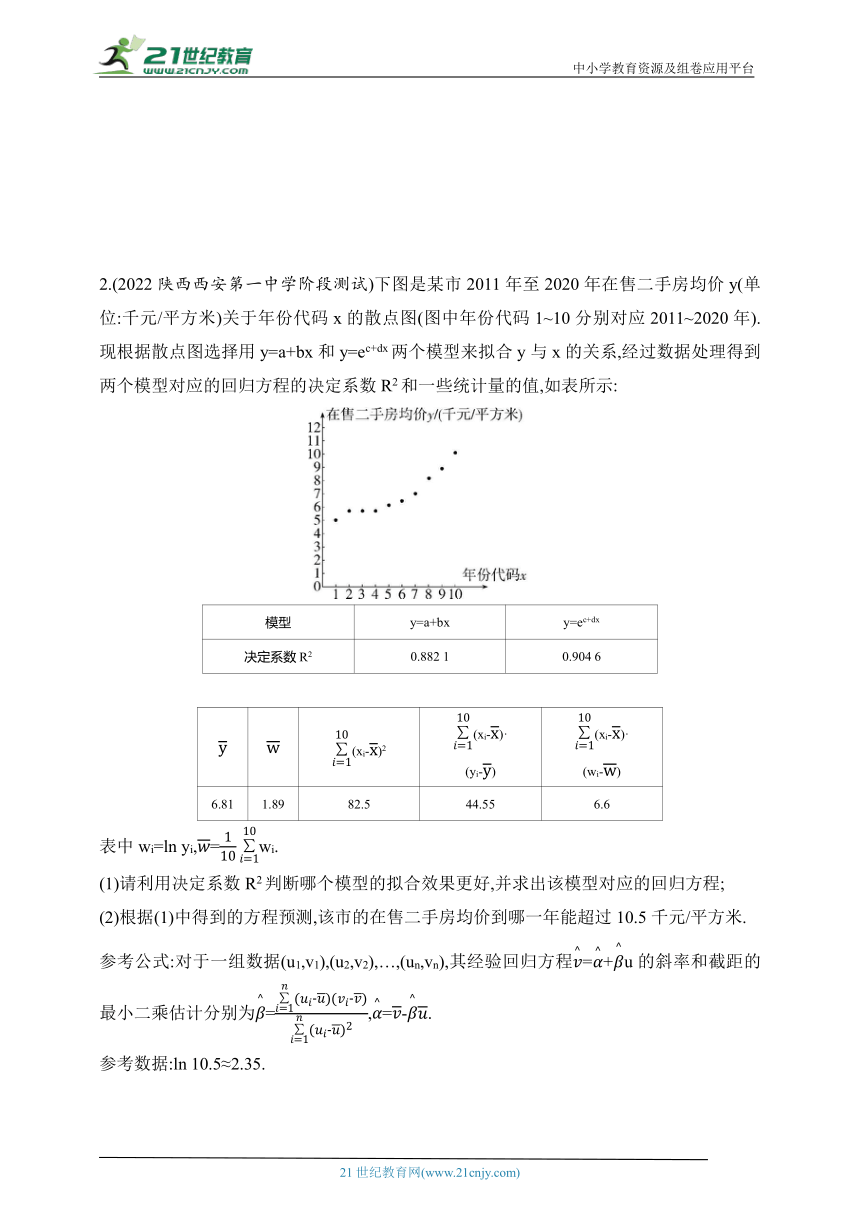
用两种模型①y=bx+a,②y=aebx分别进行拟合,得到相应的回归方程并进行残差分析,得到如下图所示的残差图及一些统计量的值.
xiyi
7 30 1 464.24 364
(1)根据残差图,比较模型①和模型②的拟合效果,应该选择哪个模型
(2)将残差的绝对值大于2的数据认为是异常数据,需要剔除.
(i)剔除异常数据后求出(1)中所选模型的回归方程;
(ii)若广告投入量为18万元,求该模型收益的预测值是多少.
附:在经验回归方程=x+中,斜率和截距的最小二乘估计分别为==,=-.
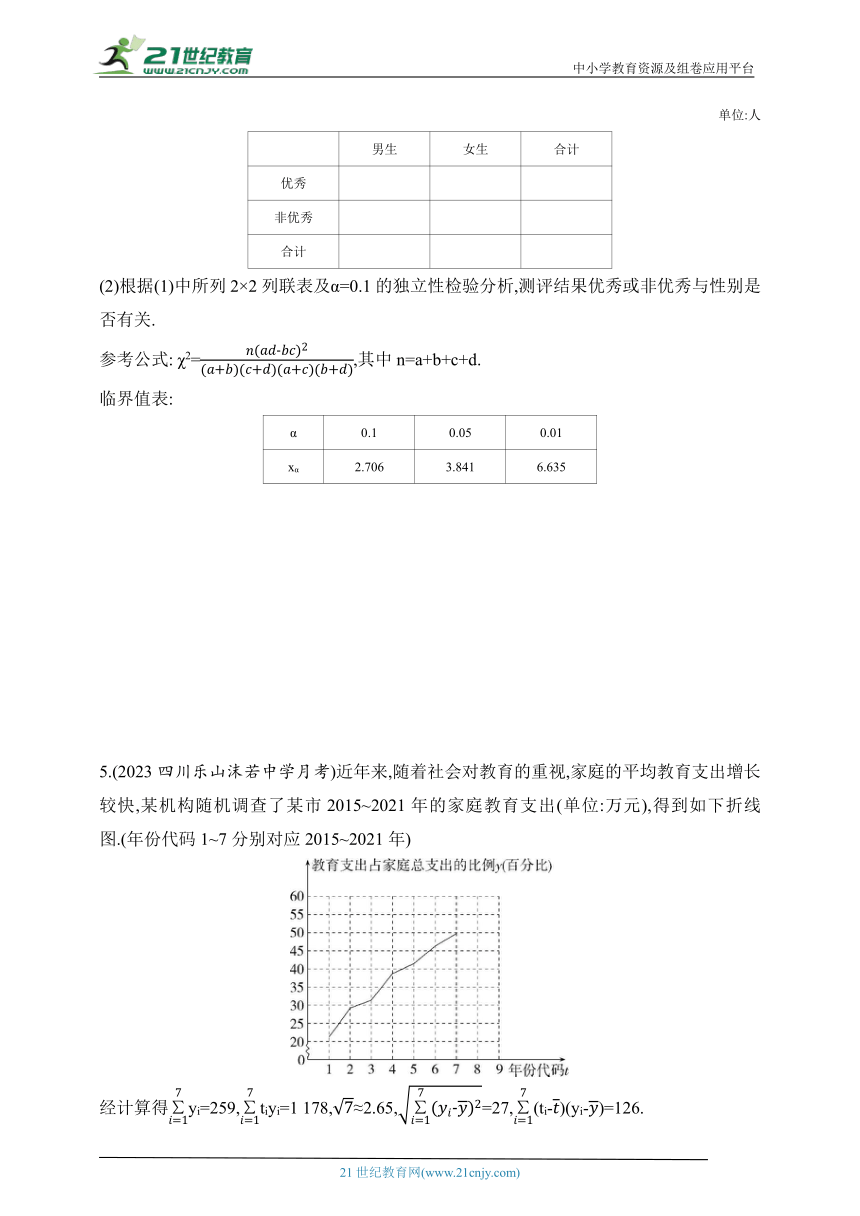
2.(2022陕西西安第一中学阶段测试)下图是某市2011年至2020年在售二手房均价y(单位:千元/平方米)关于年份代码x的散点图(图中年份代码1~10分别对应2011~2020年).现根据散点图选择用y=a+bx和y=ec+dx两个模型来拟合y与x的关系,经过数据处理得到两个模型对应的回归方程的决定系数R2和一些统计量的值,如表所示:
模型 y=a+bx y=ec+dx
决定系数R2 0.882 1 0.904 6
(xi-)2 (xi-)· (yi-) (xi-)· (wi-)
6.81 1.89 82.5 44.55 6.6
表中wi=ln yi,=wi.
(1)请利用决定系数R2判断哪个模型的拟合效果更好,并求出该模型对应的回归方程;
(2)根据(1)中得到的方程预测,该市的在售二手房均价到哪一年能超过10.5千元/平方米.
参考公式:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其经验回归方程=+u的斜率和截距的最小二乘估计分别为=,=-.
参考数据:ln 10.5≈2.35.
易错点2 用错公式致错
3.(2023河南濮阳期末)某城市选用一种植物进行绿化,设其中一株幼苗从观察之日起,第x天的高度为y cm,测得一些数据如下表所示:
第x天 1 2 3 4 5 6 7
高度y/cm 1 4 6 9 11 12 13
由表中数据可以得到y关于x的经验回归方程为=2.04x+,则第6天的残差为( )
A.-0.08 B.2.12 C.-2.12 D.0.08
4.已知中学生综合素质评价的某个维度分“优秀、合格、尚待改进”三个等级,某校在某次测评中采用的是学生互评的方式.若该校高二年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层随机抽样的方法从高二年级抽取了45名学生,了解他们的测评结果,并作出频数统计表如下:
表1:男生
等级 优秀 合格 尚待改进
频数 15 x 5
表2:女生
等级 优秀 合格 尚待改进
频数 15 3 y
(1)确定表中x,y的值,并填写下面的2×2列联表:
单位:人
男生 女生 合计
优秀
非优秀
合计
(2)根据(1)中所列2×2列联表及α=0.1的独立性检验分析,测评结果优秀或非优秀与性别是否有关.
参考公式: χ2=,其中n=a+b+c+d.
临界值表:
α 0.1 0.05 0.01
xα 2.706 3.841 6.635
5.(2023四川乐山沫若中学月考)近年来,随着社会对教育的重视,家庭的平均教育支出增长较快,某机构随机调查了某市2015~2021年的家庭教育支出(单位:万元),得到如下折线图.(年份代码1~7分别对应2015~2021年)
经计算得yi=259,tiyi=1 178,≈2.65,=27,(ti-)(yi-)=126.
(1)用线性回归模型拟合y与t的关系,求出样本相关系数r(精确到0.01),并说明y与t相关性的强弱;
(2)建立y关于t的经验回归方程;
(3)若2023年该市某家庭总支出为10万元,预测2023年该家庭的教育支出.
附:①样本相关系数r=;|r|>0.8时,认为y与t是高度相关的,即相关性很强.
②在经验回归方程=t+中,=,=-.
思想方法练
一、数形结合思想在统计中的应用
1.下图是某地区2013年至2022年污染天数y与年份x的折线图,根据2013~2017年的数据,2018~2022年的数据,2013~2022年的数据分别得到经验回归方程=x+,=x+,=x+,则( )
A.<<,<< B.<<,<<
C.<<,<< D.<<,<<
2.(2023浙江嘉兴期末)为积极响应“反诈”宣传教育活动的要求,某企业特举办了一次“反诈”知识竞赛,规定:满分为100分,60分及以上为合格.该企业从甲、乙两个车间中各抽取了100位职工的竞赛成绩作为样本,对甲车间100位职工的成绩进行统计后得到了如图所示的频率分布直方图.
(1)估算甲车间职工此次“反诈”知识竞赛的合格率;
(2)将频率视为概率,以样本估计总体.从甲车间职工中采用有放回简单随机抽样方法抽取3次,每次抽1人,每次抽取的结果相互独立,记被抽取的3人中成绩合格的人数为X,求随机变量X的分布列;
(3)若乙车间参加此次知识竞赛的合格率为60%,请根据所给数据,完成下面的2×2列联表,并根据α=0.01的独立性检验分析此次职工“反诈”知识竞赛的成绩与其所在车间是否有关.
甲车间 乙车间 合计
合格人数
不合格人数
合计
参考公式: χ2=,其中n=a+b+c+d.
临界值表:
α 0.10 0.05 0.010 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
二、转化与化归思想在统计中的应用
3.(2023江西九所重点中学联考)若所有样本点(xi,yi)(i=1,2,…,6)都在曲线y=bx2-附近波动,经计算得xi=12,yi=14,=23,则实数b的值为 .
4.(2021江西景德镇一中期末)某大型现代化农场在种植某种大棚有机无公害的蔬菜时,为创造更大价值,提高亩产量,积极开展技术创新活动.该农场采用了延长光照时间的方案,该农场选取了20间大棚(每间一亩)进行试点,得到各间大棚产量数据并绘制成散点图.光照时长为x(单位:小时),大棚蔬菜产量为y(单位:千斤/亩),记w=ln x.
(1)根据散点图判断,y=a+bx与y=c+dln x哪一个适宜作为大棚蔬菜产量y关于光照时长x的回归方程类型(给出判断即可,不必说明理由);
(2)根据(1)中判断结果及表中数据,建立y关于x的回归方程(结果保留小数点后两位);
(3)根据实际种植情况,发现上述回归方程在光照时长位于6~14小时内拟合程度良好,利用(2)中所求方程估计当光照时长为e2小时时,大棚蔬菜的产量为多少千斤/亩.
参考数据:
290 102.4 52 4 870
540.28 137 1 578.2 272.1
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其经验回归方程=u+中的斜率和截距的最小二乘估计分别为=,=-.
答案与分层梯度式解析
本章复习提升
易混易错练
1.解析 (1)由题图知,模型①的残差点比较均匀地落在水平的带状区域内,且模型①的带状区域比模型②的带状区域窄,所以模型①的拟合效果好,应选择模型①.
(2)(i)由题图知,3月份的数据为异常数据,剔除后,求得'=×(7×6-6)=7.2,'=×(30×6-31.8)=29.64,=1 464.24-6×31.8=1 273.44,=364-62=328,
所以====3,='-'=29.64-3×7.2=8.04.
所以=3x+8.04.
(ii)当x=18时,=3×18+8.04=62.04,
所以该模型收益的预测值为62.04万元.
2.解析 (1)由0.904 6>0.882 1,知模型y=ec+dx的拟合效果更好.
对y=ec+dx的两边取自然对数,得ln y=c+dx,
令w=ln y,可知w与x之间具有线性相关关系,
设w关于x的经验回归方程为=+x,
易得=×(1+2+…+10)=5.5,
则===0.08,
=-=1.89-0.08×5.5=1.45,
所以w关于x的经验回归方程为=1.45+0.08x,
故y关于x的回归方程为=e1.45+0.08x.
(2)令=e1.45+0.08x>10.5,得1.45+0.08x>2.35,解得x>11.25,取x=12,对应2022年,
所以该市的在售二手房均价到2022年能超过10.5千元/平方米.
易错警示 从题中所给多个模型中选择一个最合适的模型时,常因选择的不是最佳模型而导致错误.产生错误的原因一般有两种:一是根据散点图判断时,由于题中所给散点的个数不多,造成错误判断;二是对数据的分析过于简单,比如仅从变量间的增减进行判断,缺乏对线性与非线性、增减快与慢的分析等.
3.A 由题表得==4,==8,所以8=2.04×4+,
解得=-0.16,所以=2.04x-0.16.
当x=6时,=2.04×6-0.16=12.08,
所以第6天的残差为12-12.08=-0.08.
故选A.
易错警示 残差=观测值-预测值,解题时防止记错公式导致错误.
4.解析 (1)设采用分层随机抽样的方法从高二年级抽取的45名学生中男、女生人数分别为a,b,则有=,=,解得a=25,b=20,
故x=25-15-5=5,y=20-15-3=2.
2×2列联表如下:
单位:人
男生 女生 合计
优秀 15 15 30
非优秀 10 5 15
合计 25 20 45
(2)零假设H0:测评结果优秀或非优秀与性别无关.根据(1)中列联表得χ2==1.125<2.706=x0.1,
所以根据α=0.1的独立性检验,没有充分证据推断H0不成立,因此认为H0成立,即测评结果优秀或非优秀与性别无关.
易错警示 先根据题意准确写出2×2列联表,然后利用公式求出χ2的值,最后根据临界值表得出结论,注意χ2的计算公式中a,b,c,d的各项要准确对应,不要弄混.
5.解析 (1)由题意得=×(1+2+3+4+5+6+7)=4,
(ti-)2=(1-4)2+(2-4)2+(3-4)2+(4-4)2+(5-4)2+(6-4)2+(7-4)2=28,
故=2,
故r==≈0.88,
因为|0.88|>0.8,
所以y与t的相关性较强.
(2)易得===4.5,
=-=-4.5×4=-18=19,
所以y关于t的经验回归方程为=4.5t+19.
(3)2023年对应的年份代码t=9,
当t=9时,=4.5×9+19=59.5,
故预测2023年该家庭的教育支出为10×59.5%=5.95(万元).
易错警示 决定系数R2,样本相关系数r以及经验回归方程中的公式很相似,使用时首先要分清公式结构,不要弄混,其次数字计算都较为复杂,计算时需仔细.
思想方法练
1.C 由题中统计图可知2013~2017年,y随着x的增加平缓下降,2018~2022年,y随着x的增加迅速下降,
根据题图可直观得出污染天数y与年份x在每个阶段的关系,体现了数形结合的思想.
根据经验回归方程=x+中,的几何意义可知,>,<<0,由点的分布可知,∈(,),∈(,),所以<<,<<.故选C.
2.解析 (1)根据题图可得甲车间职工此次“反诈”知识竞赛的合格率为(0.02×10+0.03×10+0.02×10+0.01×10)×100%=80%.
(2)由题意,得X~B(3,0.8),
P(X=0)=×0.80×0.23=0.008,
P(X=1)=×0.81×0.22=0.096,
P(X=2)=×0.82×0.21=0.384,
P(X=3)=×0.83×0.20=0.512,
故随机变量X的分布列为
X 0 1 2 3
P 0.008 0.096 0.384 0.512
(3)根据题中统计数据可填写2×2列联表如下:
由题中频率分布直方图求出甲车间合格与不合格的频数.
甲车间 乙车间 合计
合格人数 80 60 140
不合格人数 20 40 60
合计 100 100 200
零假设H0:此次职工“反诈”知识竞赛的成绩与其所在车间无关.经计算得χ2=≈9.524>6.635=x0.01,所以根据α=0.01的独立性检验,有充分证据推断H0不成立,即认为此次职工“反诈”知识竞赛的成绩与其所在车间有关,此推断犯错误的概率不大于0.01.
思想方法 数形结合思想是一种非常重要的思想方法,就是把“数”与“形”巧妙地结合起来,充分应用“形”的直观性、“数”的严密性与准确性,使抽象问题直观化、复杂问题简单化,从而使问题得到解决.在回归分析问题中,利用散点图可以判断两个变量之间的相关关系.
3.答案
解析 令t=x2,则y=bt-,
通过换元将非线性回归模型转化为线性回归模型.
因为=yi=,==,
所以=b×-,解得b=.
4.解析 (1)根据题中散点图,可知开始的点在某条直线旁,但后面的点会越来越偏离这条直线,因此y=c+dln x适宜作为大棚蔬菜产量y关于光照时长x的回归方程类型.
(2)因为w=ln x,所以y=c+dln x为y=c+dw,
通过换元将对数型函数模型转化为线性回归模型进行解决.
=,
所以==≈3.26,
=-=5.12-3.26×2.6≈-3.36,
所以=3.26w-3.36,即=3.26ln x-3.36.
(3)当x=e2时,=3.26ln e2-3.36=3.16.
故估计大棚蔬菜的产量为3.16千斤/亩.
思想方法 转化与化归思想在本章中的应用主要体现在解决非线性回归问题中,即两个变量不是线性相关关系时,利用变量间的转换,把非线性回归问题转化为线性回归问题加以解决.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版高中数学选择性必修第三册同步
第八章 成对数据的统计分析
本章复习提升
易混易错练
易错点1 选错回归模型致错
1.(2023湖南长沙长郡中学检测)某互联网公司为了确定下一季度的前期广告投入计划,收集了近6个月广告投入量x(单位:万元)和收益y(单位:万元)的数据,如下表所示:
月份 1 2 3 4 5 6
广告投入 量x(万元) 2 4 6 8 10 12
收益y(万元) 14.21 20.31 31.8 31.18 37.83 44.67
用两种模型①y=bx+a,②y=aebx分别进行拟合,得到相应的回归方程并进行残差分析,得到如下图所示的残差图及一些统计量的值.
xiyi
7 30 1 464.24 364
(1)根据残差图,比较模型①和模型②的拟合效果,应该选择哪个模型
(2)将残差的绝对值大于2的数据认为是异常数据,需要剔除.
(i)剔除异常数据后求出(1)中所选模型的回归方程;
(ii)若广告投入量为18万元,求该模型收益的预测值是多少.
附:在经验回归方程=x+中,斜率和截距的最小二乘估计分别为==,=-.
2.(2022陕西西安第一中学阶段测试)下图是某市2011年至2020年在售二手房均价y(单位:千元/平方米)关于年份代码x的散点图(图中年份代码1~10分别对应2011~2020年).现根据散点图选择用y=a+bx和y=ec+dx两个模型来拟合y与x的关系,经过数据处理得到两个模型对应的回归方程的决定系数R2和一些统计量的值,如表所示:
模型 y=a+bx y=ec+dx
决定系数R2 0.882 1 0.904 6
(xi-)2 (xi-)· (yi-) (xi-)· (wi-)
6.81 1.89 82.5 44.55 6.6
表中wi=ln yi,=wi.
(1)请利用决定系数R2判断哪个模型的拟合效果更好,并求出该模型对应的回归方程;
(2)根据(1)中得到的方程预测,该市的在售二手房均价到哪一年能超过10.5千元/平方米.
参考公式:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其经验回归方程=+u的斜率和截距的最小二乘估计分别为=,=-.
参考数据:ln 10.5≈2.35.
易错点2 用错公式致错
3.(2023河南濮阳期末)某城市选用一种植物进行绿化,设其中一株幼苗从观察之日起,第x天的高度为y cm,测得一些数据如下表所示:
第x天 1 2 3 4 5 6 7
高度y/cm 1 4 6 9 11 12 13
由表中数据可以得到y关于x的经验回归方程为=2.04x+,则第6天的残差为( )
A.-0.08 B.2.12 C.-2.12 D.0.08
4.已知中学生综合素质评价的某个维度分“优秀、合格、尚待改进”三个等级,某校在某次测评中采用的是学生互评的方式.若该校高二年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层随机抽样的方法从高二年级抽取了45名学生,了解他们的测评结果,并作出频数统计表如下:
表1:男生
等级 优秀 合格 尚待改进
频数 15 x 5
表2:女生
等级 优秀 合格 尚待改进
频数 15 3 y
(1)确定表中x,y的值,并填写下面的2×2列联表:
单位:人
男生 女生 合计
优秀
非优秀
合计
(2)根据(1)中所列2×2列联表及α=0.1的独立性检验分析,测评结果优秀或非优秀与性别是否有关.
参考公式: χ2=,其中n=a+b+c+d.
临界值表:
α 0.1 0.05 0.01
xα 2.706 3.841 6.635
5.(2023四川乐山沫若中学月考)近年来,随着社会对教育的重视,家庭的平均教育支出增长较快,某机构随机调查了某市2015~2021年的家庭教育支出(单位:万元),得到如下折线图.(年份代码1~7分别对应2015~2021年)
经计算得yi=259,tiyi=1 178,≈2.65,=27,(ti-)(yi-)=126.
(1)用线性回归模型拟合y与t的关系,求出样本相关系数r(精确到0.01),并说明y与t相关性的强弱;
(2)建立y关于t的经验回归方程;
(3)若2023年该市某家庭总支出为10万元,预测2023年该家庭的教育支出.
附:①样本相关系数r=;|r|>0.8时,认为y与t是高度相关的,即相关性很强.
②在经验回归方程=t+中,=,=-.
思想方法练
一、数形结合思想在统计中的应用
1.下图是某地区2013年至2022年污染天数y与年份x的折线图,根据2013~2017年的数据,2018~2022年的数据,2013~2022年的数据分别得到经验回归方程=x+,=x+,=x+,则( )
A.<<,<< B.<<,<<
C.<<,<< D.<<,<<
2.(2023浙江嘉兴期末)为积极响应“反诈”宣传教育活动的要求,某企业特举办了一次“反诈”知识竞赛,规定:满分为100分,60分及以上为合格.该企业从甲、乙两个车间中各抽取了100位职工的竞赛成绩作为样本,对甲车间100位职工的成绩进行统计后得到了如图所示的频率分布直方图.
(1)估算甲车间职工此次“反诈”知识竞赛的合格率;
(2)将频率视为概率,以样本估计总体.从甲车间职工中采用有放回简单随机抽样方法抽取3次,每次抽1人,每次抽取的结果相互独立,记被抽取的3人中成绩合格的人数为X,求随机变量X的分布列;
(3)若乙车间参加此次知识竞赛的合格率为60%,请根据所给数据,完成下面的2×2列联表,并根据α=0.01的独立性检验分析此次职工“反诈”知识竞赛的成绩与其所在车间是否有关.
甲车间 乙车间 合计
合格人数
不合格人数
合计
参考公式: χ2=,其中n=a+b+c+d.
临界值表:
α 0.10 0.05 0.010 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
二、转化与化归思想在统计中的应用
3.(2023江西九所重点中学联考)若所有样本点(xi,yi)(i=1,2,…,6)都在曲线y=bx2-附近波动,经计算得xi=12,yi=14,=23,则实数b的值为 .
4.(2021江西景德镇一中期末)某大型现代化农场在种植某种大棚有机无公害的蔬菜时,为创造更大价值,提高亩产量,积极开展技术创新活动.该农场采用了延长光照时间的方案,该农场选取了20间大棚(每间一亩)进行试点,得到各间大棚产量数据并绘制成散点图.光照时长为x(单位:小时),大棚蔬菜产量为y(单位:千斤/亩),记w=ln x.
(1)根据散点图判断,y=a+bx与y=c+dln x哪一个适宜作为大棚蔬菜产量y关于光照时长x的回归方程类型(给出判断即可,不必说明理由);
(2)根据(1)中判断结果及表中数据,建立y关于x的回归方程(结果保留小数点后两位);
(3)根据实际种植情况,发现上述回归方程在光照时长位于6~14小时内拟合程度良好,利用(2)中所求方程估计当光照时长为e2小时时,大棚蔬菜的产量为多少千斤/亩.
参考数据:
290 102.4 52 4 870
540.28 137 1 578.2 272.1
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其经验回归方程=u+中的斜率和截距的最小二乘估计分别为=,=-.
答案与分层梯度式解析
本章复习提升
易混易错练
1.解析 (1)由题图知,模型①的残差点比较均匀地落在水平的带状区域内,且模型①的带状区域比模型②的带状区域窄,所以模型①的拟合效果好,应选择模型①.
(2)(i)由题图知,3月份的数据为异常数据,剔除后,求得'=×(7×6-6)=7.2,'=×(30×6-31.8)=29.64,=1 464.24-6×31.8=1 273.44,=364-62=328,
所以====3,='-'=29.64-3×7.2=8.04.
所以=3x+8.04.
(ii)当x=18时,=3×18+8.04=62.04,
所以该模型收益的预测值为62.04万元.
2.解析 (1)由0.904 6>0.882 1,知模型y=ec+dx的拟合效果更好.
对y=ec+dx的两边取自然对数,得ln y=c+dx,
令w=ln y,可知w与x之间具有线性相关关系,
设w关于x的经验回归方程为=+x,
易得=×(1+2+…+10)=5.5,
则===0.08,
=-=1.89-0.08×5.5=1.45,
所以w关于x的经验回归方程为=1.45+0.08x,
故y关于x的回归方程为=e1.45+0.08x.
(2)令=e1.45+0.08x>10.5,得1.45+0.08x>2.35,解得x>11.25,取x=12,对应2022年,
所以该市的在售二手房均价到2022年能超过10.5千元/平方米.
易错警示 从题中所给多个模型中选择一个最合适的模型时,常因选择的不是最佳模型而导致错误.产生错误的原因一般有两种:一是根据散点图判断时,由于题中所给散点的个数不多,造成错误判断;二是对数据的分析过于简单,比如仅从变量间的增减进行判断,缺乏对线性与非线性、增减快与慢的分析等.
3.A 由题表得==4,==8,所以8=2.04×4+,
解得=-0.16,所以=2.04x-0.16.
当x=6时,=2.04×6-0.16=12.08,
所以第6天的残差为12-12.08=-0.08.
故选A.
易错警示 残差=观测值-预测值,解题时防止记错公式导致错误.
4.解析 (1)设采用分层随机抽样的方法从高二年级抽取的45名学生中男、女生人数分别为a,b,则有=,=,解得a=25,b=20,
故x=25-15-5=5,y=20-15-3=2.
2×2列联表如下:
单位:人
男生 女生 合计
优秀 15 15 30
非优秀 10 5 15
合计 25 20 45
(2)零假设H0:测评结果优秀或非优秀与性别无关.根据(1)中列联表得χ2==1.125<2.706=x0.1,
所以根据α=0.1的独立性检验,没有充分证据推断H0不成立,因此认为H0成立,即测评结果优秀或非优秀与性别无关.
易错警示 先根据题意准确写出2×2列联表,然后利用公式求出χ2的值,最后根据临界值表得出结论,注意χ2的计算公式中a,b,c,d的各项要准确对应,不要弄混.
5.解析 (1)由题意得=×(1+2+3+4+5+6+7)=4,
(ti-)2=(1-4)2+(2-4)2+(3-4)2+(4-4)2+(5-4)2+(6-4)2+(7-4)2=28,
故=2,
故r==≈0.88,
因为|0.88|>0.8,
所以y与t的相关性较强.
(2)易得===4.5,
=-=-4.5×4=-18=19,
所以y关于t的经验回归方程为=4.5t+19.
(3)2023年对应的年份代码t=9,
当t=9时,=4.5×9+19=59.5,
故预测2023年该家庭的教育支出为10×59.5%=5.95(万元).
易错警示 决定系数R2,样本相关系数r以及经验回归方程中的公式很相似,使用时首先要分清公式结构,不要弄混,其次数字计算都较为复杂,计算时需仔细.
思想方法练
1.C 由题中统计图可知2013~2017年,y随着x的增加平缓下降,2018~2022年,y随着x的增加迅速下降,
根据题图可直观得出污染天数y与年份x在每个阶段的关系,体现了数形结合的思想.
根据经验回归方程=x+中,的几何意义可知,>,<<0,由点的分布可知,∈(,),∈(,),所以<<,<<.故选C.
2.解析 (1)根据题图可得甲车间职工此次“反诈”知识竞赛的合格率为(0.02×10+0.03×10+0.02×10+0.01×10)×100%=80%.
(2)由题意,得X~B(3,0.8),
P(X=0)=×0.80×0.23=0.008,
P(X=1)=×0.81×0.22=0.096,
P(X=2)=×0.82×0.21=0.384,
P(X=3)=×0.83×0.20=0.512,
故随机变量X的分布列为
X 0 1 2 3
P 0.008 0.096 0.384 0.512
(3)根据题中统计数据可填写2×2列联表如下:
由题中频率分布直方图求出甲车间合格与不合格的频数.
甲车间 乙车间 合计
合格人数 80 60 140
不合格人数 20 40 60
合计 100 100 200
零假设H0:此次职工“反诈”知识竞赛的成绩与其所在车间无关.经计算得χ2=≈9.524>6.635=x0.01,所以根据α=0.01的独立性检验,有充分证据推断H0不成立,即认为此次职工“反诈”知识竞赛的成绩与其所在车间有关,此推断犯错误的概率不大于0.01.
思想方法 数形结合思想是一种非常重要的思想方法,就是把“数”与“形”巧妙地结合起来,充分应用“形”的直观性、“数”的严密性与准确性,使抽象问题直观化、复杂问题简单化,从而使问题得到解决.在回归分析问题中,利用散点图可以判断两个变量之间的相关关系.
3.答案
解析 令t=x2,则y=bt-,
通过换元将非线性回归模型转化为线性回归模型.
因为=yi=,==,
所以=b×-,解得b=.
4.解析 (1)根据题中散点图,可知开始的点在某条直线旁,但后面的点会越来越偏离这条直线,因此y=c+dln x适宜作为大棚蔬菜产量y关于光照时长x的回归方程类型.
(2)因为w=ln x,所以y=c+dln x为y=c+dw,
通过换元将对数型函数模型转化为线性回归模型进行解决.
=,
所以==≈3.26,
=-=5.12-3.26×2.6≈-3.36,
所以=3.26w-3.36,即=3.26ln x-3.36.
(3)当x=e2时,=3.26ln e2-3.36=3.16.
故估计大棚蔬菜的产量为3.16千斤/亩.
思想方法 转化与化归思想在本章中的应用主要体现在解决非线性回归问题中,即两个变量不是线性相关关系时,利用变量间的转换,把非线性回归问题转化为线性回归问题加以解决.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
