变量与函数1(四川省宜宾市)
图片预览








文档简介
课件28张PPT。变量与函数如图是某地一天内的气温变化图 看图回答:
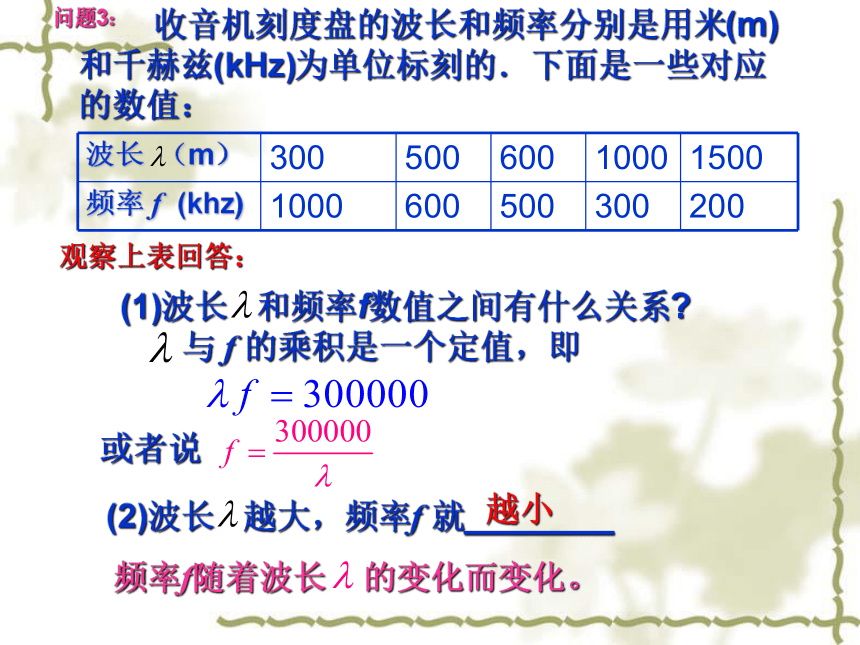
(1)这天的6时、10时和14时的气温分别为多少?任意给出这天中的某一时刻,说出这一时刻的气温.(2)这一天中,最高气温是多少?最低气温是多少?(3)这一天中,什么时段的气温在逐渐升高?什么时段的气温在逐渐降低? ··温度T随着时间t的变化而变化。问题1: 银行对各种不同的存款方式都规定了相应的利率,下表是2006年8月中国人民银行为“整存整取”的存款方式规定的年利率: 观察上表,说说随着存期x的增长,相应的年利率y是如何变化的. 随着存期x的增长,相应的年利率y也随着增长.年利率y随着存期x的变化而变化。问题2: 收音机刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数值: 观察上表回答:与 f 的乘积是一个定值,即或者说 (1)波长 和频率f数值之间有什么关系?(2)波长 越大,频率f 就________越小频率f随着波长 的变化而变化。问题3:问题4:如果用r表示圆的半径,S表示圆的面积,则S与r之间满足下列关系:S=利用这个关系式,试求出半径为1cm、1.5cm、2cm、2.6cm、3.2cm时圆的面积,并将结果填入下表:圆的半径越大,它的面积就越大圆的面积S随着半径r的变化而变化。 在上面的问题中,我们研究了一些数量关系,它们都刻画了某些变化规律.这里出现了各种各样的量,特别值得注意的是出现了一些数值会发生变化的量. 例如问题1中,刻画气温变化规律的量是时间t和气温T,气温T随着时间t的变化而变化,它们都会取不同的数值. 像这样在某一变化过程中,可以取不同数值的量,叫做变量. 例:指出下列关系式中的变量。(1)收音机刻度盘上的波长(m)与频率 f (kHz)之间的关系:是变量。是变量。是变量。问题1中的T、t,问题2 中的y、x都是变量。观察:下面的例子中有一些始终不变的量,你能找出来吗?(1)收音机刻度盘上的波长(m)与频率 f (kHz)之间的关系:3000002、 这种在问题的研究过程中,取值始终保持不变的量,称为常量。如图是某地一天内的气温变化图 ··问题1:观察:(2)当横轴上的时间t取定一个值时,纵轴上气温T有几个值与之对应?(1)题中有哪几个变量?T、t两个变量一个 银行对各种不同的存款方式都规定了相应的利率,下表是2006年8月中国人民银行为“整存整取”的存款方式规定的年利率: 问题2:观察:(2)当存期x取定一个值时,利率y有几个值与之对应?(1)题中有哪几个变量?y、x两个变量一个 收音机刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数值: 问题3:观察:(2)当波长 取定一个值时,频率 f 有几个值与之对应?(1)题中有哪几个变量?一个、f两个变量问题4:如果用r表示圆的半径,S表示圆的面积,则S与r之间满足下列关系:S=观察:(2)当半径r 取定一个值时,面积S 有几个值与之对应?(1)题中有哪几个变量?一个S、r两个变量归纳:以上四个问题有什么共同之处?(1)每个问题中出现了几个变量?2个(2)以问题2为例,在下表中年利率y随着存期x的变化而变化。两个变量分别为x和y,对于x的每一个值,y都有唯一的值与之对应。我们就说x是y是此时称y是x的函数。自变量,因变量。变量与函数一般地,如果在一个变化过程中,有两个变量,例如x和y,对于x的每一个值,y都有唯一的值与之对应。我们就说x是y是此时称y是x的函数。自变量,因变量。如图是某地一天内的气温变化图 ··问题1:函数:自变量:因变量: 银行对各种不同的存款方式都规定了相应的利率,下表是2006年8月中国人民银行为“整存整取”的存款方式规定的年利率: 问题2:函数:自变量:因变量: 收音机刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数值: 问题3:函数:自变量:因变量:问题4:如果用r表示圆的半径,S表示圆的面积,则S与r之间满足下列关系:函数:自变量:因变量:函数的三种表示方法:1. 图象法2.列表法3.解析法如问题3 中的问题4中的这些表达式称为函数的关系式。例: 写出下列各问题中的关系式,并指出其中的常量与变量:
(1)圆的周长C与半径r 的关系式;C=2π r S=60t2、180是常量,(2)火车以60千米/时的速度行驶,它驶过的路程S(千米)和所用时间 t(时)的关系式;(3) n 边形的内角和 S与边数n 的关系式.解:2、π是常量,( )r、C是变量解:解:60是常量,( )t、S是变量S=(n-2)×180( )n、S是变量. 实际问题中,写函数关系式时,一定要写出自变量的取值范围。例1、汽车离开A站5千米后,以40千米/时的平均速度行驶了t小时,汽车离开A站所走的路程s(千米)与时间t(小时)之间的函数关系式是,.t自变量是例2、下面的表格分别给出了变量 x 与 y 之间的对应关系,y 是 x 的函数吗?x 是 y 的函数吗?请说明理由.分析:y不是x的函数,因为当x=1时,y有两个值1和-1与之对应;当x=2时,y有两个值4和-4与之对应.x是y的函数,因为对于y的每一个值,x都有唯一的值与之对应.ex:1.下列关系中不是函数关系的是( )A检测反馈 1.举3个日常生活中遇到的函数关系的例子.2.分别指出下列各关系式中的变量与常量:
(1)三角形的一边长5cm,它的面积S(cm2)与这边上的高h(cm)的关系式是:;
(2)若直角三角形中的一个锐角的度数为α,则另一个锐角β(度)与α间的关系式是
(3)若某种报纸的单价为a元,x表示购买这种报纸的份数,则购买报纸的总价y(元)与x间的关系是:交流反思: 1.函数概念包含:(1)两个变量;(2)两个变量之间的对应关系.2.在某个变化过程中,可以取不同数值的量,叫做变量;数值始终保持不变的量,叫做常量.例如x和y,对于x的每一个值,y都有惟一的值与之对应,我们就说x是自变量,y是因变量.3.函数关系三种表示方法:(1)解析法;(2)列表法;(3)图象法
(1)这天的6时、10时和14时的气温分别为多少?任意给出这天中的某一时刻,说出这一时刻的气温.(2)这一天中,最高气温是多少?最低气温是多少?(3)这一天中,什么时段的气温在逐渐升高?什么时段的气温在逐渐降低? ··温度T随着时间t的变化而变化。问题1: 银行对各种不同的存款方式都规定了相应的利率,下表是2006年8月中国人民银行为“整存整取”的存款方式规定的年利率: 观察上表,说说随着存期x的增长,相应的年利率y是如何变化的. 随着存期x的增长,相应的年利率y也随着增长.年利率y随着存期x的变化而变化。问题2: 收音机刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数值: 观察上表回答:与 f 的乘积是一个定值,即或者说 (1)波长 和频率f数值之间有什么关系?(2)波长 越大,频率f 就________越小频率f随着波长 的变化而变化。问题3:问题4:如果用r表示圆的半径,S表示圆的面积,则S与r之间满足下列关系:S=利用这个关系式,试求出半径为1cm、1.5cm、2cm、2.6cm、3.2cm时圆的面积,并将结果填入下表:圆的半径越大,它的面积就越大圆的面积S随着半径r的变化而变化。 在上面的问题中,我们研究了一些数量关系,它们都刻画了某些变化规律.这里出现了各种各样的量,特别值得注意的是出现了一些数值会发生变化的量. 例如问题1中,刻画气温变化规律的量是时间t和气温T,气温T随着时间t的变化而变化,它们都会取不同的数值. 像这样在某一变化过程中,可以取不同数值的量,叫做变量. 例:指出下列关系式中的变量。(1)收音机刻度盘上的波长(m)与频率 f (kHz)之间的关系:是变量。是变量。是变量。问题1中的T、t,问题2 中的y、x都是变量。观察:下面的例子中有一些始终不变的量,你能找出来吗?(1)收音机刻度盘上的波长(m)与频率 f (kHz)之间的关系:3000002、 这种在问题的研究过程中,取值始终保持不变的量,称为常量。如图是某地一天内的气温变化图 ··问题1:观察:(2)当横轴上的时间t取定一个值时,纵轴上气温T有几个值与之对应?(1)题中有哪几个变量?T、t两个变量一个 银行对各种不同的存款方式都规定了相应的利率,下表是2006年8月中国人民银行为“整存整取”的存款方式规定的年利率: 问题2:观察:(2)当存期x取定一个值时,利率y有几个值与之对应?(1)题中有哪几个变量?y、x两个变量一个 收音机刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数值: 问题3:观察:(2)当波长 取定一个值时,频率 f 有几个值与之对应?(1)题中有哪几个变量?一个、f两个变量问题4:如果用r表示圆的半径,S表示圆的面积,则S与r之间满足下列关系:S=观察:(2)当半径r 取定一个值时,面积S 有几个值与之对应?(1)题中有哪几个变量?一个S、r两个变量归纳:以上四个问题有什么共同之处?(1)每个问题中出现了几个变量?2个(2)以问题2为例,在下表中年利率y随着存期x的变化而变化。两个变量分别为x和y,对于x的每一个值,y都有唯一的值与之对应。我们就说x是y是此时称y是x的函数。自变量,因变量。变量与函数一般地,如果在一个变化过程中,有两个变量,例如x和y,对于x的每一个值,y都有唯一的值与之对应。我们就说x是y是此时称y是x的函数。自变量,因变量。如图是某地一天内的气温变化图 ··问题1:函数:自变量:因变量: 银行对各种不同的存款方式都规定了相应的利率,下表是2006年8月中国人民银行为“整存整取”的存款方式规定的年利率: 问题2:函数:自变量:因变量: 收音机刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数值: 问题3:函数:自变量:因变量:问题4:如果用r表示圆的半径,S表示圆的面积,则S与r之间满足下列关系:函数:自变量:因变量:函数的三种表示方法:1. 图象法2.列表法3.解析法如问题3 中的问题4中的这些表达式称为函数的关系式。例: 写出下列各问题中的关系式,并指出其中的常量与变量:
(1)圆的周长C与半径r 的关系式;C=2π r S=60t2、180是常量,(2)火车以60千米/时的速度行驶,它驶过的路程S(千米)和所用时间 t(时)的关系式;(3) n 边形的内角和 S与边数n 的关系式.解:2、π是常量,( )r、C是变量解:解:60是常量,( )t、S是变量S=(n-2)×180( )n、S是变量. 实际问题中,写函数关系式时,一定要写出自变量的取值范围。例1、汽车离开A站5千米后,以40千米/时的平均速度行驶了t小时,汽车离开A站所走的路程s(千米)与时间t(小时)之间的函数关系式是,.t自变量是例2、下面的表格分别给出了变量 x 与 y 之间的对应关系,y 是 x 的函数吗?x 是 y 的函数吗?请说明理由.分析:y不是x的函数,因为当x=1时,y有两个值1和-1与之对应;当x=2时,y有两个值4和-4与之对应.x是y的函数,因为对于y的每一个值,x都有唯一的值与之对应.ex:1.下列关系中不是函数关系的是( )A检测反馈 1.举3个日常生活中遇到的函数关系的例子.2.分别指出下列各关系式中的变量与常量:
(1)三角形的一边长5cm,它的面积S(cm2)与这边上的高h(cm)的关系式是:;
(2)若直角三角形中的一个锐角的度数为α,则另一个锐角β(度)与α间的关系式是
(3)若某种报纸的单价为a元,x表示购买这种报纸的份数,则购买报纸的总价y(元)与x间的关系是:交流反思: 1.函数概念包含:(1)两个变量;(2)两个变量之间的对应关系.2.在某个变化过程中,可以取不同数值的量,叫做变量;数值始终保持不变的量,叫做常量.例如x和y,对于x的每一个值,y都有惟一的值与之对应,我们就说x是自变量,y是因变量.3.函数关系三种表示方法:(1)解析法;(2)列表法;(3)图象法
