文英高一对数函数复习

文英高一对数函数复习
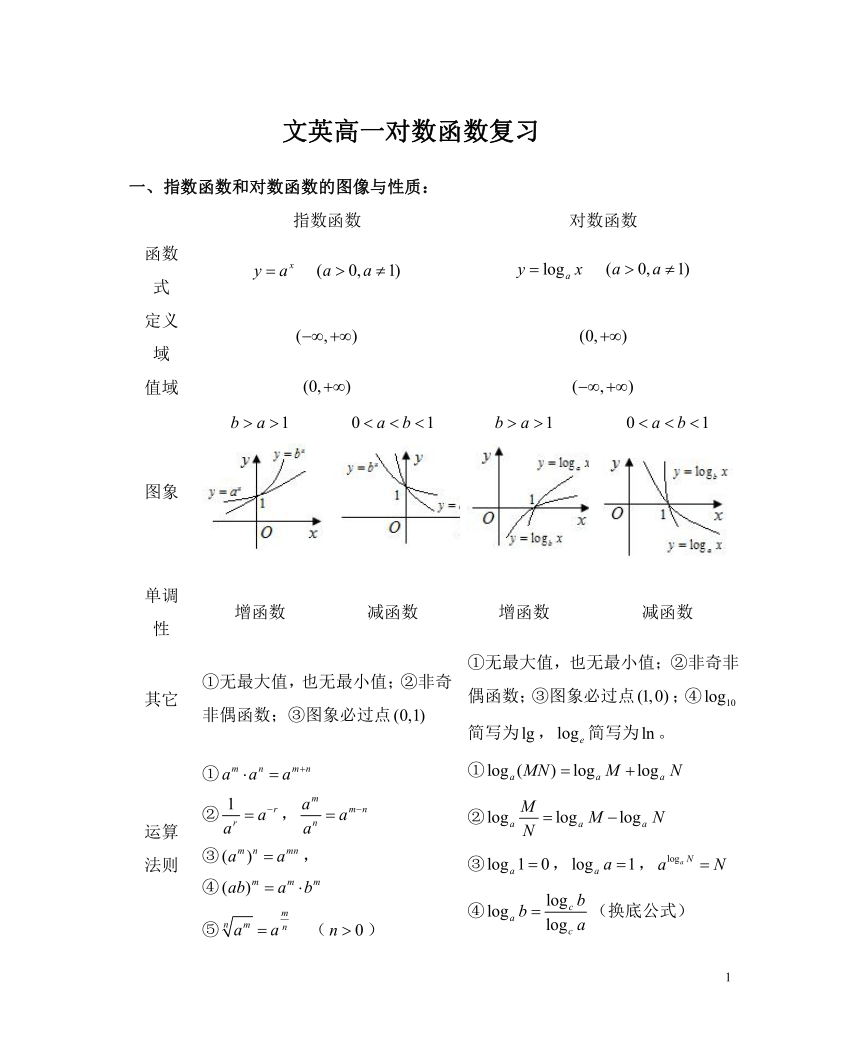
一、指数函数和对数函数的图像与性质：
指数函数
对数函数
函数式


定义域
值域
图象
单调性
增函数
减函数
增函数
减函数
其它
①无最大值，也无最小值；②非奇非偶函数；③图象必过点
①无最大值，也无最小值；②非奇非偶函数；③图象必过点；④简写为，简写为。
运算
法则
①
②，
③，
④
⑤ （）
①
②
③，，
④（换底公式）
二、知识应用与解题研究：
1. 若，则的表达式为（ D ）
A． B． C． D．
2. 以下四个数中的最大者是（ D ）
A.(ln2)2 B. ln(ln2) C. ln D. ln2
3．设，，，则（　A　）
Ａ． Ｂ． Ｃ． Ｄ．
4.设f(x)＝，则的定义域为（ B ）
A. B.(－4,－1)(1，4) C. (－2,－1)(1，2) D. (－4,－2)(2，4)
5．已知函数 （ B ）
A． B．－ C．2 D．－2
6.若定义在区间（-1，0）内的函数满足ｆ（ｘ）＞0，则ａ的取值范围是（ A ）
A. B. C. D.
7．设是奇函数，则使的的取值范围是 （ A ）
A． B． C． D．
8.设，，，则（ A ）
A． B． C． D．
9．函数y=logax在上总有|y|>1，则a的取值范围是 （ B ）
A．或 B．或
C． D．或
[解析]：∵函数y=logax在上总有|y|>1
当0< <1 时 ，函数y=logax在上总有y< -1
即
当时，函数y=logax在上总有y>1
即
由①②可得
10.已知是上的减函数，那么的取值范围是( C )
A. B. C. D.
11．方程的根的情况是 （ C ）
A．仅有一根 B．有两个正根
C．有一正根和一个负根 D．有两个负根
12．已知函数，则实数a值是（ B ）
A．1 B． C． D．－1
13、已知对任意都有意义，则实数的取值范围是
14．已知，则方程的实根个数为___2个_________
15、已知函数的定义域为，则实数的取值范围是或
16.使成立的的取值范围是 (-1,0)
17、若函数（>0且≠1）的值域为，则实数的取值范围是或
18．如图，A，B，C为函数的图象上的三点，它们的横坐标分别是t, t+2, t+4(t1).
(1)设ABC的面积为S 求S=f (t) ；
(2)判断函数S=f (t)的单调性；
(3) 求S=f (t)的最大值.
解 (Ⅰ)易知D为线段AB的中点, 因A(a, log2a ), B(a+4, log2(a+4)),
所以由中点公式得D(a+2, log2 ).
(Ⅱ)S△ABC=S梯形AA′CC′+S梯形CC′B′B- S梯形AA′B′B=…= log2,
其中A′,B′,C′为A,B,C在x轴上的射影.
由S△ABC= log2>1, 得0< a<2-2.
19．设A、B是函数y= log2x图象上两点, 其横坐标分别为a和a+4, 直线l: x=a+2与函数y= log2x图象交于点C, 与直线AB交于点D.
(Ⅰ)求点D的坐标;
(Ⅱ)当△ABC的面积大于1时, 求实数a的取值范围.
(16)解 (Ⅰ)易知D为线段AB的中点, 因A(a, log2a ), B(a+4, log2(a+4)),
所以由中点公式得D(a+2, log2 ).
(Ⅱ)S△ABC=S梯形AA′CC′+S梯形CC′B′B- S梯形AA′B′B=…= log2,
其中A′,B′,C′为A,B,C在x轴上的射影.
由S△ABC= log2>1, 得0< a<2-2.
20. 已知常数, 变数x、y有关系.若,
(1)试以a、t表示y ;
(2)若t在内变化时, y有最小值8, 求此时a和x的值各为多少?
13. (1)
.
(2)
时,