复数代数形式的加减运算及其几何意义
文档属性
| 名称 | 复数代数形式的加减运算及其几何意义 |  | |
| 格式 | rar | ||
| 文件大小 | 53.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-03-18 14:20:00 | ||
图片预览






文档简介
课件14张PPT。 复数代数形式的加减运算
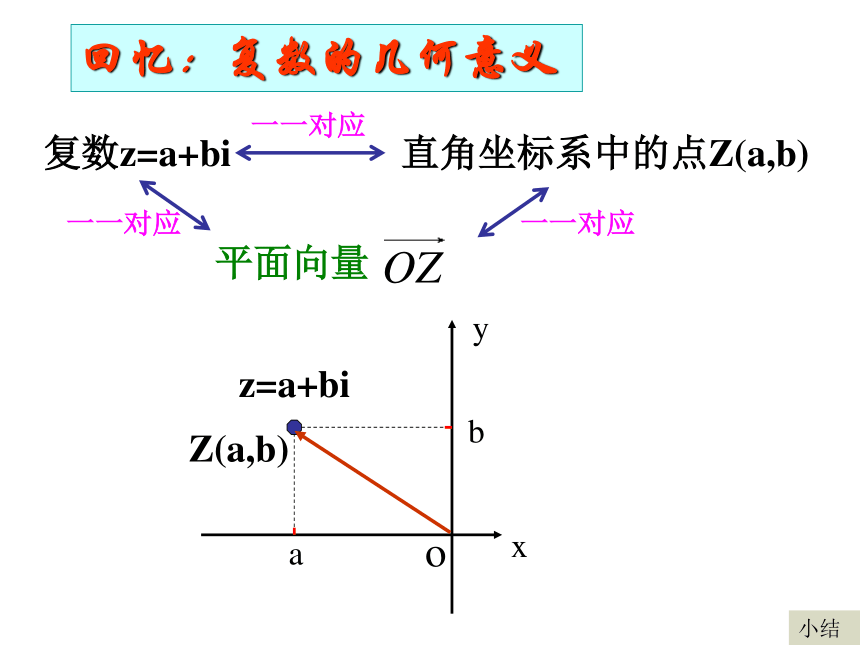
及其几何意义一、复数的加、减法Z1+Z2=Z2+Z1两个复数的和依然是一个复数,它的实部是原来的两个复数实部的和,它的虚部是原来的两个复数虚部的和交换律:设Z1=a+bi(a,b∈R) Z2=c+di(c,d∈R)1、加法:则Z1+Z2=(a+bi)+(c+di)=(a+c)+(b+d)i结合律:(Z1+Z2)+Z3=Z1+(Z2+Z3)实数有加法和减法运算,且减法是加法的逆运算。思考:复数的减法如何定义?类比实数的减法运算两个复数的差依然是一个复数,它的实部是原来的两个复数实部的差,它的虚部是原来的两个复数虚部的差设Z1=a+bi(a,b∈R) Z2=c+di(c,d∈R)2、减法:则Z1-Z2=(a+bi)-(c+di)=(a-c)+(b-di)复数z=a+bi直角坐标系中的点Z(a,b)一一对应平面向量一一对应一一对应回忆:复数的几何意义xyobaZ(a,b)z=a+bi小结二、复数加法的几何意义复数的加法可以按照向量的加法进行,这是复数加法的几何意义。二、复数减法的几何意义复数的加法可以按照向量的加法进行,这是复数加法的几何意义。类比复数加法的几何意义,复数减法的几何意义是什么?复数的减法可以按照向量的
减法进行,这是复数减法的
几何意义。例1、计算(1) (1+3i)+(-4+2i)
(2) (5-6i)+(-2-i)-(3+4i)
(3) 已知(3-ai)-(b+4i)=2a-bi,
求实数a、b的值。说明:二、共轭复数:实部相等而虚部互为相反数的两个复数,叫做互为共轭复数.虚部不等于0的两个共轭复数也叫做共轭虚数。定义:关于实轴对称(2)(D)小结Z1+Z2=Z2+Z1两个复数的和依然是一个复数,它的实部是原来的两个复数实部的和,它的虚部是原来的两个复数虚部的和交换律:1、复数加法:Z1+Z2=(a+bi)+(c+di)=(a+c)+(b+di)结合律:(Z1+Z2)+Z3=Z1+(Z2+Z3)2、减法:Z1-Z2=(a+bi)-(c+di)=(a-c)+(b-di)3、几何意义:复数的加法可以按照向量的加法进行,复数的减法可以按照向量的减法进行。
4、共轭复数:
减法进行,这是复数减法的
几何意义。例1、计算(1) (1+3i)+(-4+2i)
(2) (5-6i)+(-2-i)-(3+4i)
(3) 已知(3-ai)-(b+4i)=2a-bi,
求实数a、b的值。说明:二、共轭复数:实部相等而虚部互为相反数的两个复数,叫做互为共轭复数.虚部不等于0的两个共轭复数也叫做共轭虚数。定义:关于实轴对称(2)(D)小结Z1+Z2=Z2+Z1两个复数的和依然是一个复数,它的实部是原来的两个复数实部的和,它的虚部是原来的两个复数虚部的和交换律:1、复数加法:Z1+Z2=(a+bi)+(c+di)=(a+c)+(b+di)结合律:(Z1+Z2)+Z3=Z1+(Z2+Z3)2、减法:Z1-Z2=(a+bi)-(c+di)=(a-c)+(b-di)3、几何意义:复数的加法可以按照向量的加法进行,复数的减法可以按照向量的减法进行。
4、共轭复数:
